递归分析在带噪语音端点检测中的应用
贾 亮,尹 伊,杨慧超(沈阳航空航天大学 电子信息工程学院,沈阳 110136)
递归分析在带噪语音端点检测中的应用
贾 亮,尹 伊,杨慧超
(沈阳航空航天大学 电子信息工程学院,沈阳 110136)
噪声环境下语音端点检测的难度会大大提高,递归分析是一种非线性动力学分析方法,可以更好地表示语音特征,应用消除趋势项的递归分析法对带噪语音进行分析,实现带噪语音的起止点检测。通过对比传统的谱熵端点检测法,针对在信噪比为0dB与-5dB的语音信号进行仿真,结果表明,递归分析端点检测法能更好地分割语音段与噪声段。
谱熵;递归度;端点检测;带噪语音
端点检测在语音合成与识别领域中具有重要作用,端点检测可以把语音段部分进行定位,找出某一个需要的语音段的起始点和终止点,从而为下一步的工作做好准备。由于噪声的影响,端点检测依旧是当今热点难点话题,传统的端点检测包括谱熵检测、倒谱距离检测、双门限检测等,为了提高低信噪比下性能以及对检测效果的要求越来越高,随即更多针对不同情形下端点检测的算法与观点被提出。
20世纪80年代,Eckmann等提出了在二维空间图形上观察时间序列递归性,并针对二维空间递归性在m维相空间上的轨道进行研究,表明各个时刻的递归现象可以通过二维方阵用黑点或者白点表示。这种表示方法被称作递归图(RecurrencePlot,即RP)。为了量化递归图中表现出来的系统递归现象,Zbilut等提出了定量递归分析(Recur-rence Quantification Analysis,即RQA)来描述系统不同的动力学行为[1]。
递归算法是基于一种非线性动力学分析方法,相空间重构为其来源根基,反应的是复原后的混沌吸引子所具有的某种规律,揭示时间序列的内部结构[2-3]。在端点检测中语音段与非语音段的轨迹状态的特征大不相同,是阐明时间序列周期性、混沌性以及非平稳性的一个重要方法[4]。
由于噪声的影响端点检测的精度大大下降,本文提出了基于语音信号非线性动力学特性递归分析方法。首先拟合消除趋势项函数,降低干扰与误差,再利用递归度区分语音段和非语音段,通过对比传统的谱熵法与递归分析法,表明递归分析的端点检测法有很好的效果,可利用递归法来实现语音的端点检测。
1 语音端点检测的递归分析
1.1 语音信号递归图
递归图[5]较适用于短时带噪语音的端点检测分析,可更好检验语音时间序列的平稳性、内在相似性,进而区分语音的语音段与非语音段。递归图法最初由Eckmann等人于1987年提出,主要应用于对非线性动力系统的研究[6-8]。现在,递归图已经成功地应用到多个领域,如信号分析、脑心电图分析以及故障分析等诸多领域。定量递归分析[9](recurrence quantification analysis,RQA)是基于递归图中的水平线及垂直线以及对角线等分布对系统进行分析,从而获得动力学系统的定量信息[10-12],可以描述语音的端点检测。
递归图采用图形映射方式来表现信号中所存在的结构在正常情况下得到一组带噪的语音信号,其序列就包含了非线性特征。它反应了动力系统中产生的时间序列的所有可能时间尺度上的自相关[12]。因此,递归图可以被认为揭示了语音信号中全局相关结构的。递归图利用相空间重构的思想将时间序列进行重构。选择适合的延迟时间Δt与嵌入维数m重构动力学向量Xk=(x(k),x(k+Δt),…,x(k+(m-1)Δt)),(k=1,2,…,N) ,即把语音的时间序列重构成m维的相空间轨迹,从动力学系统角度上实现了在高维空间恢复吸引子[13],引入符号函数。

(1)
计算相空间行列向量Xi、Xj距离为
(2)
计算递归值,得到矩阵的图形表示为
Ri,j=H(ε-Si,j),(i,j=1,2,…,N)
(3)
ε为临界距离,将所求得Ri,j值映射到二维图中,如图1所示。

图1 语音信号递归图
当矩阵中任意两个矢量间的距离Si,j≤ε时,意味着坐标(i,j)取值为1,递归图(i,j) 位置上表示为黑点,相反为0则在递归图(i,j)位置上表示为白点。黑点与白点所组成的二维递归图可以清晰地描述各个状态之间的递归关系,其实质是用二维图形来展示高维相空间中轨迹随时间的演化情况图形结构,主要由孤立点、对角线、水平线以及垂直线等组成[13]。整个递归图表现了语音信号语音段与非语音段的全局系统。
1.2 改进型语音信号的递归分析
递归图中黑白点的分布反应带噪语音信号中语音段与非语音段的内在相似结构。由于语音信号的动力学差异,语音段在递归图中黑点的比例往往比非语音的段小,可以将递归率作为区分语音段和非语音段的一种方法。定量递归分析结果表明:语音信号中较高的递归率[4]意味着较强的周期性嵌入,递归率公式如式所示:
(4)
其中N为递归图上的节点数,RRl反应了相空间相点密集程度。
本文引入另一种描述语音端点检测的方法递归图的熵[14]。不难发现随着多种线长度的变化语音信号的递归图中,熵值也会产生较大变化。用来描述信号递归图的复杂程度,结构愈复杂熵值就愈高,递归图中变量是线的长度。若所有线长度都为同一值则熵为0,语音熵计算公式为
(5)
其中,p(l)表示语音信号递归图中对角线分布的概率密度。定量递归分析表明:语音信号的确定性越强,RQA中的确定率与熵值就越大,如图2、图3所示。

图2 信噪比为20 dB的递归图

图3 信噪比为10 dB的递归图
随着噪声强度的增大,递归图中时间序列受噪声影响越大,递归图中对角线越短,此时熵值越混乱,展现了语音信号在带噪情况下的全局系统。
2 消除趋势项

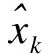
(6)
其中k=1,2,…,n,定义误差项为最小,即:
(7)
令误差项为最小即:

(8)
最终拟合趋势项为
(9)
语音信号中通常m=1~3,语音信号偏差值如表1所示。

表1 语音信号偏离基线值
3 递归在端点检测中的应用
本文在MATLAB环境下,对短时语音加入信噪比为0 dB与-5 dB的高斯白噪声,首先对短时带噪语音序列做消除趋势项处理,降低趋势项误差,使递归计算更加精准。并对语音序列做递归分析,采用简单的回避嵌入理论的方案[10],设定m=1,τ=1 ,临界距离直接选取语音序列标准差使ε=s。对比低信噪比下语音信号做递归分析,与传统谱熵法端点检测进行比较,结果如下所示。

图4 较纯净语音下递归与谱熵端点检测对比

图5 0 dB噪声下下递归与谱熵端点检测对比

图6 -5 dB噪声下下递归与谱熵端点检测对比
图4中较纯净的语音下语音段与噪声段的分界十分明显,递归法与谱熵法均有很好的区分语音段与噪声段效果。
图5与图6中均加入了低信噪比高斯白噪声,噪声使原始语音的语音段变得难以区分,其中前60帧与后20帧为非语音段,60帧至130帧为语音段。图5 (c)与图6(c)中由于噪声的加入使谱熵值高于图1(c)中较纯净语音,且区分噪声与语音程度有所下降,反映了低信噪比下语音的无序性,信噪比越低图形越散乱,语音起止点难以判断。图5(b)与图6(b)中由于加噪后语音段较低信噪比的噪声信号有更大的周期性与规律性,利用加噪后产生的语音序列时间尺度上的自相关性质。利用相空间重构方法将语音序列进行重构,相空间距离的变化导致递归值随之改变,且均在语音起点第60帧与语音结束的第130帧与非语音段有明显界限。递归分析的端点检测具有更好的稳定性,全面地反应了语音段与非语音段的区别,检测的准确率优于传统的谱熵法。
4 结论
语音信号存在不确定性,利用最小二乘拟合趋势项拟合信号减小系统所带来的误差,语音信号序列应用非线性动力学的方法将其映射在二维递归图中,语音序列在递归图上的表现出一定规律,再利用递归分析的方法分析表示这一规律,利用这种性质将其运用于短时带噪语音的端点检测中,在信噪比为0dB与-5dB条件下,对比传统谱熵端点检测法,可以明显地看出,递归度端点检测具有更好的效果,但不难发现递归算法的计算量很大,为此,需要进一步努力探索新模型。
[1] 郭兴明,李传鹏,卢德林.定量递归分析和近似熵在心音分类识别中的应用[J].数据采集与处理,2013,28(5):559-564.
[2] 潘玉荣,贾朝勇.基于递归图的电价信号复杂度描述[J].洛阳师范学院学报,2013,32(2):11-15.
[3] 王景芳,许慧燕.基于递归分析的基音检测新方法[J].计算机工程与应用,2012,48(13):125-129.
[4] 闫润强,祖漪清,朱贻盛.递归趋势分析在汉语语音声韵母切分中的应用研究[J].信号处理,2007,23(4):521-525.
[5] JR W C,ZBILUT J P.Dynamical assessment of physiological systems and states using recurrence plot strategies[J].Journal of Applied Physiology,1994,76(2):965-73.
[6] 杨照芳.心跳间期和皮肤电信号中的情感响应模式研究[D].重庆:西南大学,2015.
[7] 陈静.舰船辐射噪声的混沌特征提取方法研究[D].西安:西北工业大学,2006.
[8] 史玲娜.基于道路交通的相空间重构[J].重庆交通大学学报(自然科学版),2006,25(6):112-115.
[9] THIEL M,ROMANO M C,KURTHS J,et al.Influence of observational noise on the recurrence quantification analysis[J].Physica D Nonlinear Phenomena,2002,171(3):138-152.
[10]惠晓威,李坤.动力学特征分析在语音端点检测中的应用[J].计算机应用与软件,2013(12):299-302.
[11]袁昌松,雷敏,朱向阳.基于定量分析方法的动作表面肌电信号分析[J].生物物理学报,2006,22(2):139-143.
[12]李红岩.认知无线电系统中频谱可预测性的递归定量分析[J].电讯技术,2015,55(2):124-128.
[13]金宁德,陈万鹏.混沌递归分析在油水两相流流型识别中的应用[J].化工学报,2006,57(2):274-280.
[14]郭洁,陈祥献,黄海.交叉递归图在变压器铁芯压紧力变化检测中的应用[J].高电压技术,2010,36(11):2731-2738.
[15]宋知用.MATLAB在语音信号分析与合成中的应用[M].北京:北京航空航天大学出版社,2013:101-103.
Endpointdetectionofnoisyspeechbasedonrecursiveanalysis
JIA Liang,YIN Yi,YANG Hui-chao
(College of Electronic and Information Engineering,Shenyang Aerospace University,Shenyang 110136,China)
In this paper,the recursive analysis method is used to analyze the noisy speech.It is a nonlinear dynamic analysis method and can better represent the voice features.The recursive analysis method that can eliminate the trend item is applied to the analysis of the noisy speech,which can detect the start and end of the noisy speech.The speech signals at SNR 0dB and-5dB are simulated.The results show that the recursive analysis based endpoint detection method can better segment the speech and noise comparing to the traditional spectral entropy endpoint detection method.
spectral entropy;recursive degree;endpoint detection;noisy speech
2017-07-10
贾 亮(1971-),男,辽宁大石桥人,副教授,主要研究方向:信号与信息处理,E-mail:jiayw@ sina.com。
2095-1248(2017)06-0083-04
TN912.3
A
10.3969/j.issn.2095-1248.2017.06.014
刘划 英文审校:齐义文)

