基于粗糙集的城市道路拥挤度模糊评价方法

公维勇

(重庆交通大学交通运输学院，重庆 400074)

基于粗糙集的城市道路拥挤度模糊评价方法

公维勇

(重庆交通大学交通运输学院，重庆 400074)

运用粗糙集相关理论，通过道路平均运行速度、密度、延误、服务交通量与通行能力之比(V/C)等交通判别指标，建立了拥挤度评价结论与评价指标间的映射关系，经过对评价指标的约简及其权重的确定，得到了城市道路拥挤度评价模型及模糊评价方法。

城市交通；拥挤度；模糊评价；粗糙集

1 城市道路拥挤度评价的指标与评价标准

对应于道路服务水平的等级划分，把道路的拥挤度也划分为畅通C1，正常C2，拥挤C3和堵塞C4四级，等级论域为C={道路的拥挤程度}，C={C1，C2，C3，C4}。在确保对道路拥挤度评价准确性和全面性的前提下，按照专家经验建立初始指标体系，城市道路拥挤度评价的指标体系包括四个方面：路段的行驶车速、车辆密度、交通延误、服务交通量与通行能力之比(V/C)等。

最初建立的初始指标体系包括9项指标：路段平均行驶车速(X1)、车辆密度(X2)、服务交通量与通行能力之比(V/C)(X3)、服务水平(X4)、信号交叉口排队延误(X5)、信号交叉口排队长度(X6)、道路占用率(X7)、干道车流延误率(X8)、干道里程延误(X9)，X={X1，X2，X3，X4，X5，X6，X7，X8，X9}。

定义1 令P 为一等价关系集，且p∈P，当ind(p) = ind(P - p)时，称p为P中不必要的；否则称p为P中必要的。若每一个p∈P 都为P中必要的，则称P是独立的；设Q⊆P，若Q是独立的，且ind (P) = ind (Q)，则称Q为P的一个约简。P中所有必要关系的集合，称为P的核。

根据定义1，可以将原来的9个评价指标约简为4个指标：路段平均行驶车速、车辆密度、信号交叉口排队延误、服务交通量与通行能力之比(V/C)。令约简后的评价指标集为U，路段平均行驶车速为U1、车辆密度为U2、信号交叉口排队延误为U3、服务交通量与通行能力之比(V/C)为U4，则U={U1，U2，U3，U4}。

C(x)=α1U1(x)+α2U2(x)+α3U3(x)+α4U4(x)

其中：αi(i=1，2，…，4)为评价指标权重。

实用于本文的城市道路拥挤度的交通评价指标的评价标准如表1所示。

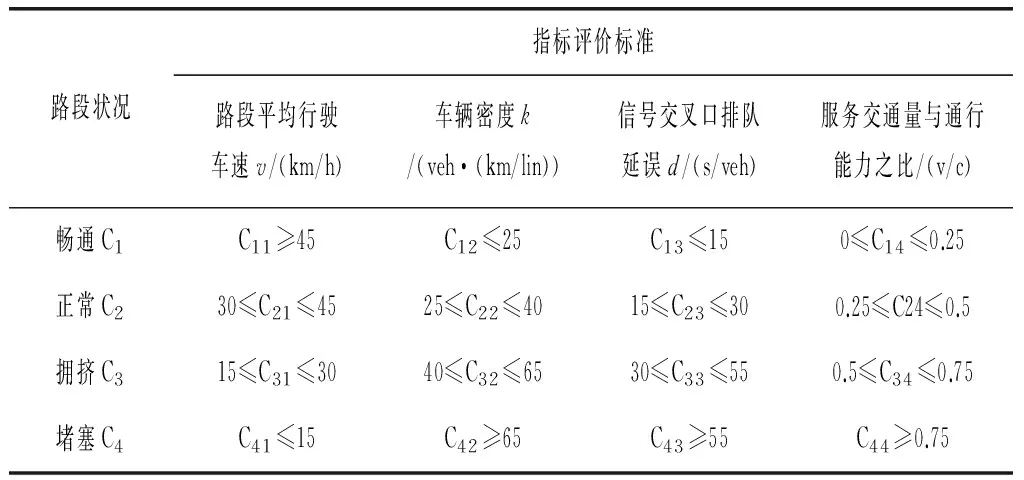
表1 交通评价指标的评价标准

2 城市道路拥挤度评价指标权重的确定

定义2 设S=(U，A，V，f)是一个信息系统，P⊆A，U/ind(P) = {X1，X2，…，Xn} ,则知识P的信息量定义为：

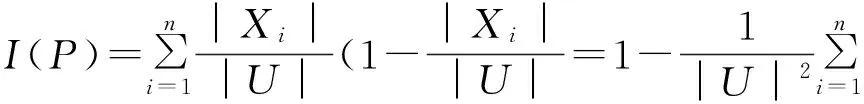
(1)

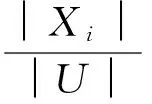
定义3 设S= (U，A，V，f) 是一个信息系统，属性a∈A在A中的重要性定义为:

SA(a)=I(A)-I(A-{a})

(2)

显然当A={a}时，SA(a)=I({a})。这说明属性a∈A在A中的重要性由A中去掉a后引起的信息量变化的大小来度量。

定义4 设S= (U,A,V,f) 是一个信息系统，则属性ai∈A={a1,a2,…,an}的权重为:

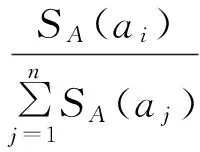
(3)

根据公式(1)-(3)，计算得到城市道路拥挤度各评价指标的权重分别为：路段平均行驶车速0.2，车辆密度0.2，信号交叉口排队延误0.25，服务交通量与通行能力之比0.35。

3 基于粗糙集的评价模型及方法

城市道路拥挤度评价就是通过分析道路上车辆行驶速度、车辆密度、行车延误、服务水平等交通参数，得到城市道路交通拥挤度评估结果。

U上的判别因子模糊集为

(4)

式中:u1，u2，u3分别为判别因子U1，U2，U3的隶属度，即分别考虑这些判别因子对效果等级所起作用的大小权重。

论域的模糊子集为

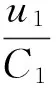
(5)

式中:u1，u2，u3，u4分别为判别等级C1，C2，C3，C4的隶属度。显然等级论域C和交通指标判别因子论域U之间存在着一种模糊关系, 若用rij表示第i个交通指标判别因子对第j个等级的隶属度，则可以得到判别因子论域与等级论域之间的模糊关系评价矩阵，这种模糊关系可以用4×4维的模糊关系矩阵表示。

(6)

令权重集W=(w1,w2,…,wm)，把W与R的合成结果视为评价者综合各种因素后对被评价对象做出的最终评价, 即模糊综合评判向量

D=W·R=(d1,d2,…,dn) (7)

基于粗糙集的城市道路拥挤度评价方法步骤为：

第一步：利用粗糙集的相关理论对城市道路拥挤度评价指标进行约简；

第二步：确定城市道路拥挤度评价各指标的权重；

第三步：再利用模糊综合评判模型进行计算。

现在假设有某城市路段某方向一个数据X=(42，35，22，0.43)。在公式(8)中，u1=0.2，u2=0.2，u3=0.25，u4=0.35，以此公式进行计算，得结果如下：

C11(42)=1,C12(35)=0,C13(22)=1,C14(0.43)=0

C1=0.2×1+0.2×0+0.25×1+0.35×0=0.45

C21(42)=1,C22(35)=1,C23(22)=1,C24(0.43)=1

C2=0.2×1+0.2×1+0.25×1+0.35×1=1

C31(42)=0,C32(35)=0,C33(22)=0,C34(0.43)=0

C3=0.2×0+0.2×0+0.25×0+0.35×0=0

C41(42)=0,C42(35)=0,C43(22)=0,C44(0.43)=0

C4=0.2×0+0.2×0+0.25×0+0.35×0=0

最大值为C2，根据最大属隶属原则，X相对地隶属于C2，所以可以判断当前该路段该方向的交通状态为正常。

4 结 论

本文运用粗糙集相关理论，建立了城市道路拥挤度评价结论与评价指标的函数，对评价指标进行约简并确定其权重，得到评价模型及方法。

[1] 张起森，张亚平.道路通行能力分析[M].北京：人民交通出版社，2002.

[2] 熊萍，程华斌，吴晓平.基于粗糙集理论的一种综合定权法[J] .海军工程大学学报，2003，15(1)：53-56.

[3] 刘磊，张举兵，杨新苗.基于出行时间的交通拥挤指数及其评价标准[J].交通与计算机，2003，(25)：97-100.

U492

C

1008-3383(2017)10-0216-02

2017-05-11

公维勇(1980-)，男，山东人，重庆交通大学讲师。