基于DQM的空间轴对称流体饱和多孔热弹性柱体动力学特性研究

朱媛媛， 胡育佳， 程昌钧， 郑晓妹

(1.上海师范大学 信息与机电工程学院，上海 200234； 2. 上海理工大学 机械工程学院，上海 200093； 3. 上海大学 力学系，上海 200093)

基于DQM的空间轴对称流体饱和多孔热弹性柱体动力学特性研究

朱媛媛1， 胡育佳2， 程昌钧3， 郑晓妹1

(1.上海师范大学 信息与机电工程学院，上海 200234； 2. 上海理工大学 机械工程学院，上海 200093； 3. 上海大学 力学系，上海 200093)

在热局部平衡条件下研究了空间轴对称不可压流体饱和多孔热弹性柱体在表面温度载荷作用下的动力学特性。基于de Boer多孔介质混合物理论，给出了问题的数学模型；其次综合采用微分求积方法-二阶向后差分法-Newton-Raphson迭代法求解了数学模型，得到柱体各离散点处未知物理量的数值结果，进而可分析柱体的动力学特性。为了验证该方法的正确性，计算了不可压流体饱和多孔弹性柱体的动力固结问题，并与de Boer等的解析结果进行了比较，两者吻合良好，也证明DQM有较小的计算量和较高的精度。最后分别研究和比较了柱体只受到表面外载荷作用下的动力学特性和受到两种表面温度载荷与外载荷联合作用下的动力学特性，考察了材料的某些参数对柱体动力学特性的影响。

流体饱和多孔热弹性柱体；多孔介质混合物理论(PMT)；空间轴对称；微分求积法(DQM)；热动力学特性

近年来，饱和多孔介质热-流-固耦合系统的动力学行为已得到国内外学者的广泛重视。由于饱和多孔介质中固相骨架和孔隙流体之间具有不同的物理和力学性能，因此固相和液相之间存在着与孔隙结构密不可分的相互作用；同时，孔隙流体的运动不仅有扩散效应，而且常伴随热反应的发生，如：核废料污染物在地下低渗透岩土中的传热-传质问题、石油天然气开发过程中的流固耦合问题、地热储层的合理开发和利用问题中的流固耦合问题等，这些问题都可看作是饱和多孔介质热-流-固耦合作用的结果。所以，对饱和多孔介质力学热力学性能与行为的研究是典型的多场耦合问题，不仅在土力学、水文学等经典应用领域发挥重要作用，也已成为许多新兴学科和应用技术发展的关键，相关理论和数值方法的研究具有重要的理论意义和广泛的应用背景。

目前，研究多孔介质宏观力学行为的理论主要有：Biot理论、多孔介质混合物理论和杂交混合物理论等。Biot[1]建立了饱和多孔介质热弹性和热动力理论，成功地应用于诸多工程领域，取得了众多成果。近年来，基于Biot理论，Cui等[2]引入热孔隙度状态表面的概念，提出了饱和土热-水力-力学耦合分析的一个较完整的理论模型。Wu等[3]提出了非饱和土热-水力-力学本构模型。刘干斌等[4]利用Fourier变换研究了荷载作用下地基土体的热-水-力耦合动力响应问题。白冰[5]分析了各向同性饱和多孔介质热-水-力一维耦合系统在循环温度荷载下的响应。

但是Biot理论是建立在力学直观基础上的，其中耦合质量项的引入与连续介质力学相违背。因此，需要建立更加精确的宏观数学理论来描述饱和多孔介质的力学行为。近年来由de Boer等[6-7]发展起来的多孔介质混合物理论, 采用公理化方法和体积分数概念研究多孔介质的力学问题, 将若干微观性质直接用来描述宏观性质，避免了Biot理论的非相容性和杂交混和物理论[8-9]中的繁杂公式，同时较容易反映某些动力学和非线性效应，为研究饱和土的力学行为提出了另一条新途径。基于多孔介质混合物理论，de Boer等[10]利用Laplace变换给出了一维动力学响应的解析解。Heider等[11]研究了在饱和多孔半空间介质中波的传播。Hu等[12]研究了黏弹性流体饱和多孔介质的动力学特性。de Boer等[13]给出了多孔介质热动力学行为的本构关系。He等[14]建立了热局部非平衡条件下不可压饱和多孔弹性介质热-流-固耦合模型，Yang[15]建立了相应的Gurtin型广义变分原理。Qin等[16]建立了非饱和土的热-水-力耦合分析模型，可反映热膨胀、热渗流、水的相变、气体溶解及土骨架变形等现象的耦合过程。Ehlers等[17]考虑了多孔介质中传质传热问题。

本文基于de Boer多孔介质混合物理论，在热局部平衡条件下，研究了空间轴对称流体饱和多孔热弹性柱体在表面温度载荷作用下的动力学特性。首先给出了问题的数学模型，然后分别在空间域内采用微分求积法(DQM)，时间域内采用二阶向后差分格式离散控制方程、边界条件和初始条件，最后运用Newton-Raphson法进行迭代求解，可得到柱体各离散点处未知物理量的数值结果。为了验证本文方法的正确性，文中计算了无热效应时不可压流体饱和多孔弹性柱体的动力学固结问题，并与1993年de Boer等利用Laplace变换得到的解析解进行了比较，两者吻合良好，证明DQM具有计算量小，精度高，数值稳定等优点。最后在热局部平衡条件下，利用本文方法研究了空间轴对称流体饱和多孔热弹性柱体只受到表面外载荷作用下的动力学特性和受到两种表面温度载荷与外载荷联合作用下的动力学特性，考察了材料的某些参数对柱体动力学特性的影响，得到了一些有益的结论。

1 问题的数学描述

1.1 控制微分方程

考察图1所示的空间轴对称不可压流体饱和多孔热弹性柱体。设柱体固相和液相的温度变化相同θS=θF=θ，即柱体处于热局部平衡状态，基于de Boer多孔介质混合物理论，对各向同性线性热弹性多孔固相骨架和理想流相，在两相不可压、小变形、小流速的假设下，任意rz平面上柱体的基本未知量满足如下控制微分方程。

图1 rz-平面上柱体的物理模型Fig.1 The physical model of cylinder on the rz-plane

质量守恒方程为

(1)

忽略体积力，动量和动量矩守恒方程为

Svwr+βθ,r=0

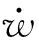
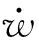
(2)

能量守恒方程为

(3)

几何关系为

(4)

假设固相材料是线性弹性热各向同性的，本构关系为

(5)

(6)

1.2 边界条件

假定柱体上表面为理想排水，给定温度变化φ(r,t)并承受时间相关垂直载荷q(r,t)作用，底部为刚性不排水且绝热；侧表面的径向位移受到约束且绝热非排水(图1)。有如下边界条件。

上表面(0≤r≤r1，z=0)的边界条件

(7a)

底部(0≤r≤r1，z=h)的边界条件

ur=0,uz=0,p,z=0,θ,z=0

(7b)

侧表面(r=r1,0≤z≤h)的边界条件

(7c)

对称轴(r=0,0≤z≤h)上的对称性条件

(7d)

1.3 初始条件

假设t≤0时柱体处于静止，初始条件为

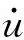
(8)

这样，式(1)～(6)，边界条件(7)和初始条件(8)构成了不可压空间轴对称流体饱和多孔热弹性柱体6个基本未知量(即固相位移ur,uz，流相相对速度wr,wz，孔隙压p和变温θ)满足的控制微分方程。

2 求解控制方程的DQM

由初边值问题式(1)～(8)可见，获得问题的解析解或半解析解是困难的。这里将采用微分求积方法(DQM)在空间域内离散控制方程和边界条件，再采用二阶向后差分格式来处理时间导数，最后，在离散化的初始条件(8)下运用Newton-Raphson迭代方法求离散化代数方程组的解，从而可得各离散点未知量的数值结果。

2.1 微分求积方法简介

20世纪70年代，Bellman等[18-19]提出了一种新的数值方法，即微分求积法(DQM)，由于DQM不依赖泛函和变分原理，具有公式简单、使用方便、精度高、计算量少等优点，引起人们广泛关注，并成功应用于许多领域[20-22]。DQM思想是将未知函数对某方向自变量的偏导数近似表达为其各离散点(节点)处相应函数值的加权和，其中，权系数与具体问题无关，而只与解区域中所选择的试函数和离散点有关。因此，利用DQM，任何微分方程都能转化为相应的代数方程。本文亦将用DQM来对基本场方程进行空间离散，关于DQM的基本原理和公式，可以参考文献[18-19]。

考虑在区域Ω={(r,z)|0≤r≤r1,0≤z≤h}内的函数Ψ(r,z)，采用Chebyshev-Lobatto多项式零点作为节点的坐标，分别沿r,z方向布置Nr×Nz个节点(图2)，根据DQM，函数Ψ(r,z)在节点r=rξ，z=zη处对自变量r的n阶偏导数可近似表示为

(9)

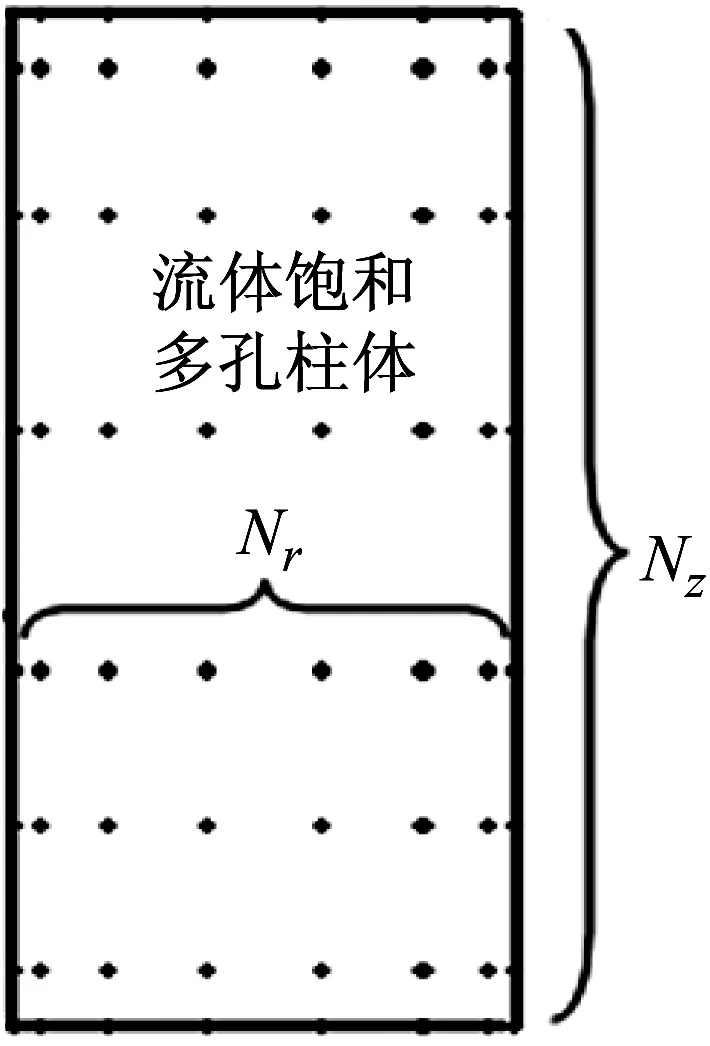
图2 rz-平面上的布点Fig.2 Nodes collocated on the rz-plane

2.2 空间域内控制方程的DQ离散化

利用公式(9)在任意rz-平面内离散控制微分方程(1)～(3)，可得rz-平面上空间域内DQ离散化方程为

(10a)

(10b)

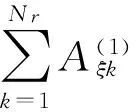
(10c)

(10d)

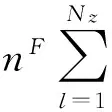
(10e)

(10f)

其中，ξ=2,3…,Nr-1,η=2,3…,Nz-1。

由几关何系(4)，应变分量的DQ离散化形式为

(11)

其中，ξ=1,2,3…,Nr,η=1,2,3…,Nz。

本构关系(5)的离散化形式为

(12)

式中，ξ=1,2,3…,Nr,η=1,2,3…,Nz。

同时，固相有效应力分量与总应力分量关系(6)的离散化形式为

(13)

式中，ξ=1,2,3…,Nr,η=1,2,3…,Nz。

式(10)～(13)构成基本场方程(1)～(6)空间域内DQ离散化形式，它是关于时间t的代数-微分方程组。

2.3 对称轴上奇异性条件的处理

当r→0

(14)

当r→0

(15)

式中，η=1,2，…，Nz。

2.4 边界条件的DQ离散化

柱体上表面(ξ=1,2,…,Nr,η=1)边界条件的DQ离散化形式为

(p)ξ1=0, (θ)ξ1=φξ1

(16a)

式中，qξ1,φξ1是ξ=1,2,…,Nr,η=1处外载荷q(r,t)和温度载荷φ(r,t)的值。

底部(ξ=1,2,…,Nr,η=Nz)边界条件的DQ离散化形式为

(ur)ξNz=0,(uz)ξNz=0,

(16b)

侧表面(ξ=Nr,η=1,2,…,Nz)边界条件的DQ离散化形式为

(16c)

对称轴(ξ=1,η=1,2,…,Nz)上对称性条件的DQ离散化形式为

(16d)

2.5 DQ离散化方程的简化

为了提高求解速度，可由公式(10b)～(10c)解出未知量(wr)ξη和(wz)ξη代入 (10a),(10d)～(10g)中，离散化方程(10)转化为在离散点(ξ,η)处只有4个未知量 (ur)ξη,(uz)ξη,(p)ξη，(θ)ξη的方程组。

2.6 时间导数的二阶向后差分格式

离散化方程(10)～(16)是一组关于时间t的代数-微分方程，将采用二阶向后差分格式来离散函数φ(t)关于时间的导数

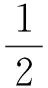
(17)

式中：Δt为时间步长；φ(tn,x)为在t=tn时刻的函数值。

利用式(17), 对DQ离散化方程组式(10)～式(16)进行时间离散，并在离散化的初始条件式(8)下，利用Newton-Raphson迭代方法求解离散化代数方程组，从而可得各离散点各未知量的数值结果。

3 流体饱和多孔热弹性柱的动力学特性

3.1 数值结果的验证

de Boer等利用Laplace变换得到了不可压一维无限长圆柱体在表面荷载作用下动力固结问题的解析解，本文运用DQM求解该问题，并与de Boer等的解析解进行比较，以说明本文方法的正确性，结果的可靠性。考虑高h=10 m，半径r1=1 m的不可压流体饱和多孔弹性体，其上边界为理想排水，并承受时间相关垂直载荷q(t)的作用；底部边界为刚性不排水；侧表面为不排水边界，流相和固相的材料参数见表1。

考虑两种垂直载荷q(t)：① 阶梯载荷q(t)=q0h(t)；② 周期载荷q(t)=q0[1-cos(ωt)]，其中，q0=3 kN/m2，ω=75 s-1，h(t)是Heaviside函数。

表1 流体饱和土的材料参数Tab.1 Physical parameters of fluid-saturated soil

图3和图4给出了在对称轴上不同深度处的沉降uz，其中，点为解析解，实线和虚线为利用DQM得到的数值解，分别对应Δt=0.01 s和Δt=0.02 s，计算中取Nr=Nz=7。可以看到，用本文方法来计算流体饱和多孔弹性介质的动力学特性是有效的，也证明本方法具有很高的精度和收敛性。

3.2 空间轴对称流体饱和多孔热弹性柱的动力学特性

考察高h=10 m，半径r1=1 m的体内无热源不可压空间轴对称流体饱和多孔热弹性柱体，边界条件如图1所示，材料参数见表2。计算中取Nr=Nz=7，Δt=1 s。

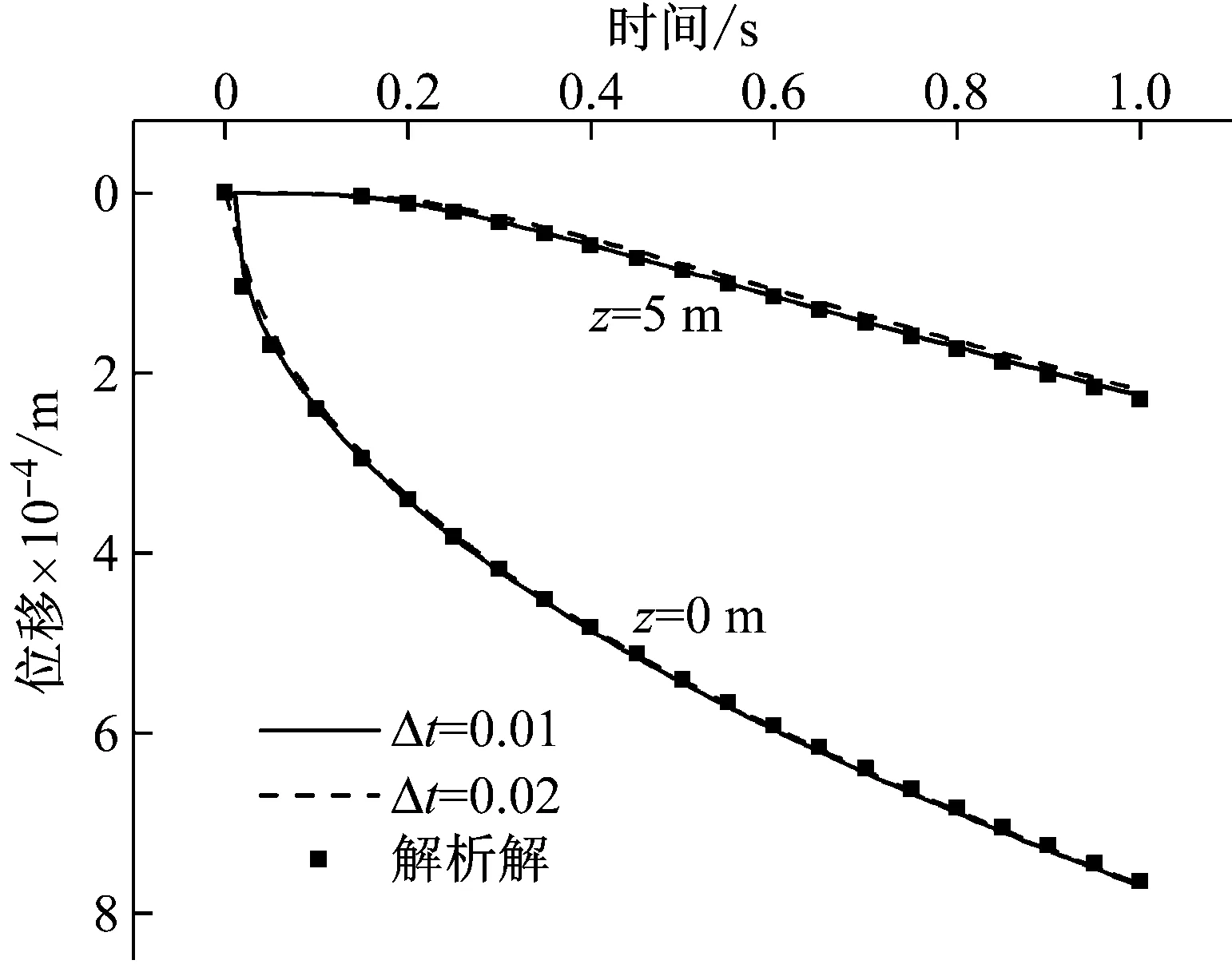
图3 阶梯载荷作用下沉降的时-程曲线Fig.3 Time-history curves of the settlement under the step loading

图4 周期载荷作用下沉降的时-程曲线Fig.4 Time-history curves of the settlement under the cycle loading表2 热-流-固耦合系统材料参数Tab.2 Physical parameters of thermo-fluid-solid system

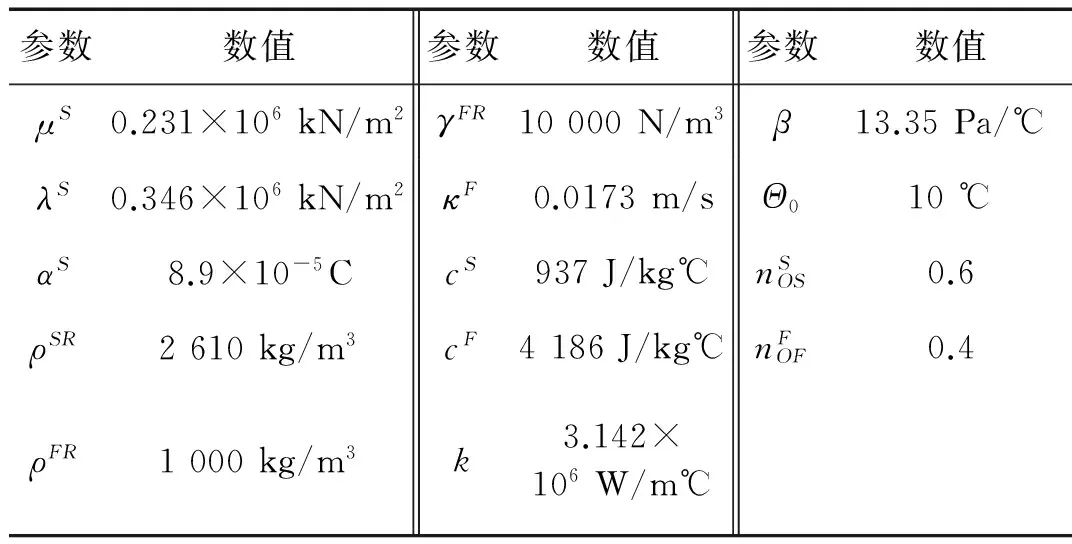
参数数值参数数值参数数值μS0.231×106kN/m2γFR10000N/m3β13.35Pa/℃λS0.346×106kN/m2κF0.0173m/sΘ010℃αS8.9×10-5CcS937J/kg℃nSOS0.6ρSR2610kg/m3cF4186J/kg℃nFOF0.4ρFR1000kg/m3k3.142×106W/m℃

3.2.1 柱体上表面仅受外载荷作用时的动力学特性

Hu等[12]利用DQM得到了空间轴对称流体饱和多孔弹性柱体的动力学特性，其模型中并没有考虑热效应的影响。假设在本文给出的流体饱和多孔热弹性柱体模型中，柱体上表面无温度变化，即φ(r,t)=0，考虑两种模型下柱体的动力学特性。

考虑两种垂直载荷q(t)：① 阶梯载荷q(t)=q0h(t)；② 周期载荷q(t)=q0[1-cos(ωt)]，其中，q0=3 kN/m2，ω=0.4 s-1，h(t)是Heaviside函数。

图5和图6为利用DQM求得的柱体对称轴不同深度处的沉降uz，流速wz，孔隙压p和应力σzz，图中实线为利用本文模型(考虑热效应)得到的结果，圆点为利用文献[12]中模型(不考虑热效应)得到的结果。由于现在考虑的问题是柱体上表面无温度改变，可近似认为柱体温度变化θ=0，即常温状态，则利用两种模型得到的解应趋于一致。计算中也验证了这一点。进一步说明本文理论和方法的正确性，结果的可靠性。此时柱体动力学特性结论可参考文献[12]。

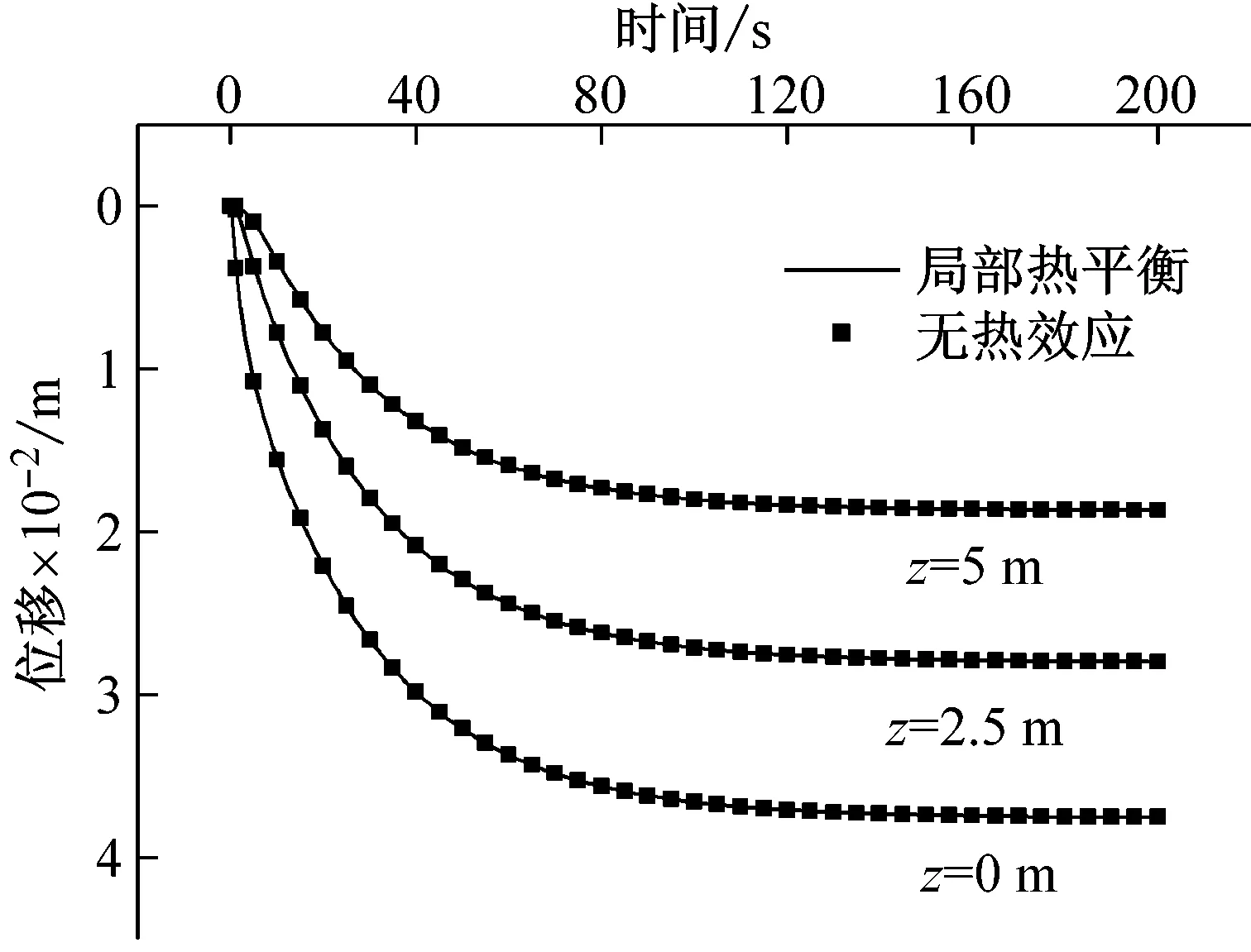
(a) 沉降

(b) 相对流速

(c) 孔隙压

(d) 应力图5 阶梯载荷作用下柱体的时-程曲线Fig.5 Time-history curves of the cylinder under the step loading

3.2.2 柱体上表面在温度载荷和外载荷联合作用下的动力学特性

给定柱体上表面外载荷q(r,t)=3 kN/m2。同时分别考察两种表面温度φ(t)对柱体动力学特性的影响：① 阶梯温度载荷φ(t)=φ0h(t)；② 周期温度载荷φ(t)=φ0[1-cos(ωt)]，其中，φ0=10 ℃，ω=0.4 s-1，h(t)是Heaviside函数。

本文考察和分析了达西渗透系数κF，热交换系数β，热传导系数k等对柱体动力学特征的影响，为了节省篇幅，仅列出了达西渗透系数κF影响的计算结果，并进行了讨论，对于β，k等参数的影响只列出了结论。

(1) 在阶梯温度载荷和外载荷情况下的结果

图7给出了在阶梯温度载荷和外载荷作用下，不同的达西渗透系数κF对对称轴不同深度处的沉降uz，相对流速wz，孔隙压p及温度变化θ的影响。

从图7(a)中可以看到，在不同的κF下，柱体沉降随着时间的增大趋于相同稳定值。当κF较大时，固结作用过程快于热传导过程，初始阶段固相的热体积膨胀效应未得到明显体现，柱体沉降大。当κF较小时，热传导过程快于机械载荷下的固结作用，初始阶段首先表现为固相的热体积膨胀效应，而后固结作用才逐渐发挥作用。

图7(b)指出，柱体流速随时间增大逐渐趋于零。在初始阶段，柱体上表面附近的流速大于内部的流速。当κF增大时，初始阶段流速的峰值增大。

图7(c)指出，柱体的孔隙压由初始值逐渐消散至零，且上表面附近孔隙压的消散速度快于内部的消散速度；当κF增大时，孔隙压消散速度增大。

从图7(d)中可以看到，柱体温度随时间的增加逐渐上升并由上表面向纵深处传导和扩散，最后达到等温状态，但κF对温度影响较小。

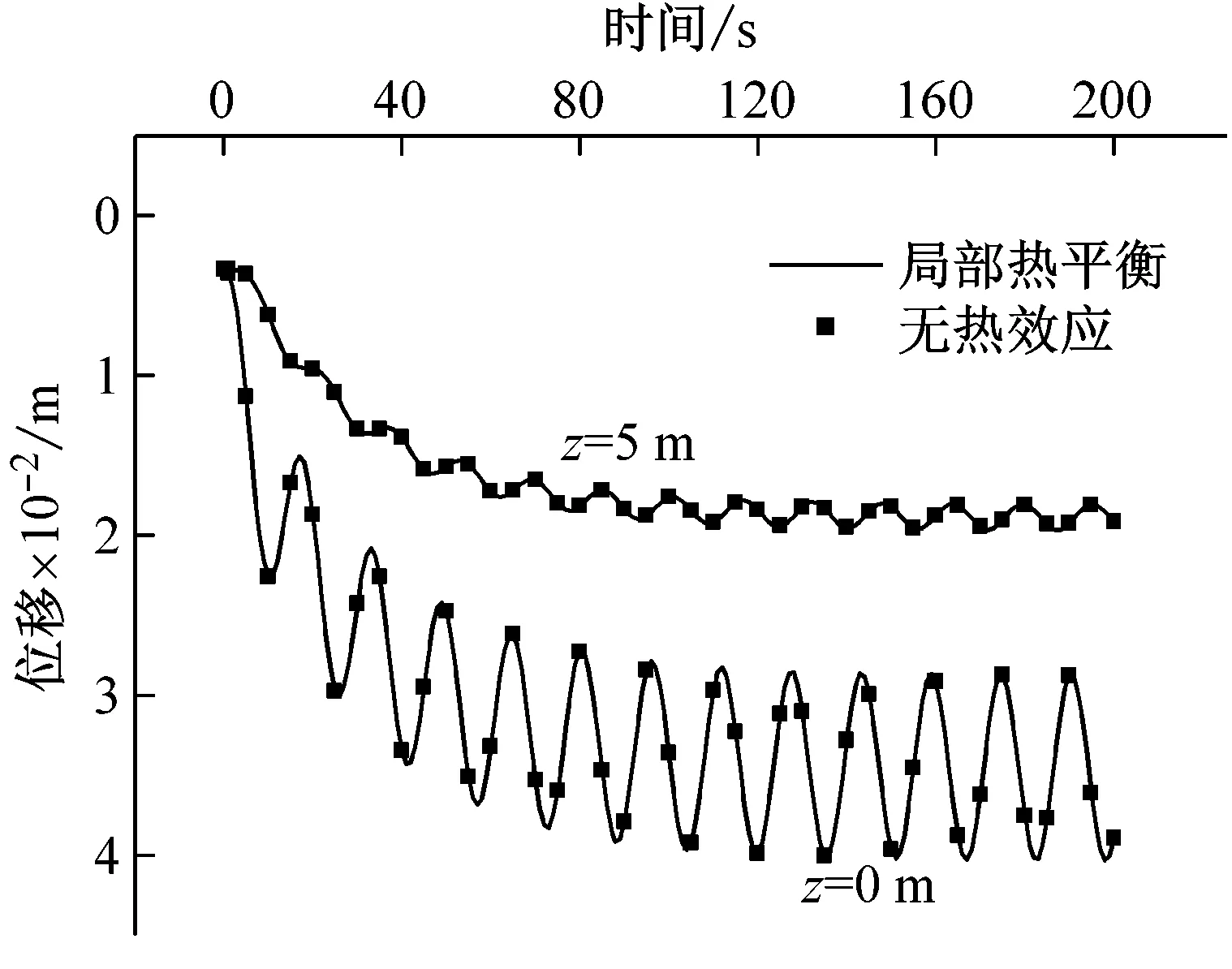
(a) 沉降

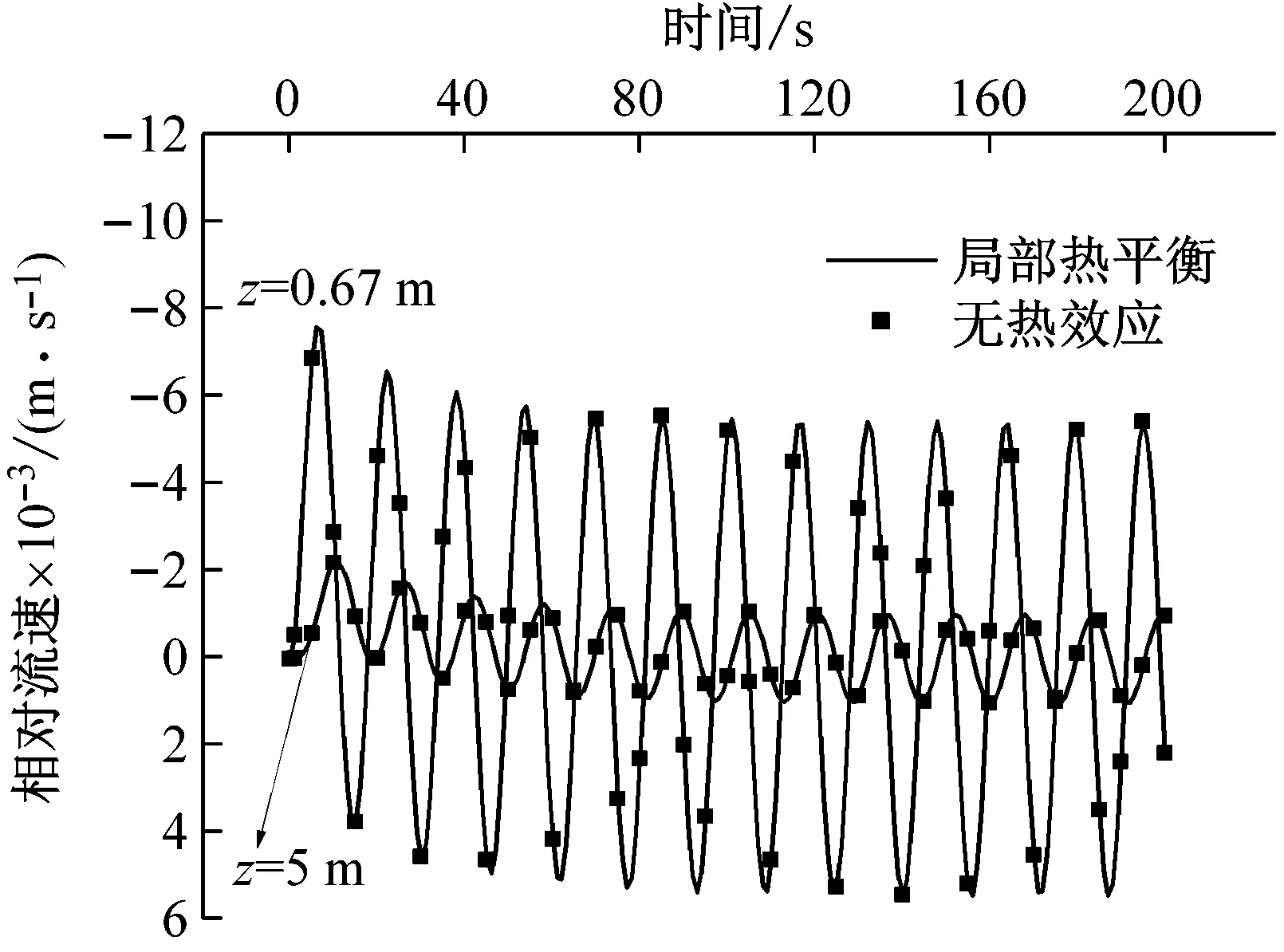
(b) 相对流速

(c) 孔隙压

(d) 应力图6 周期载荷作用下柱体的时-程曲线Fig.6 Time-history curves of the cylinder under the cycle loading

(a) 沉降

(b) 相对流速

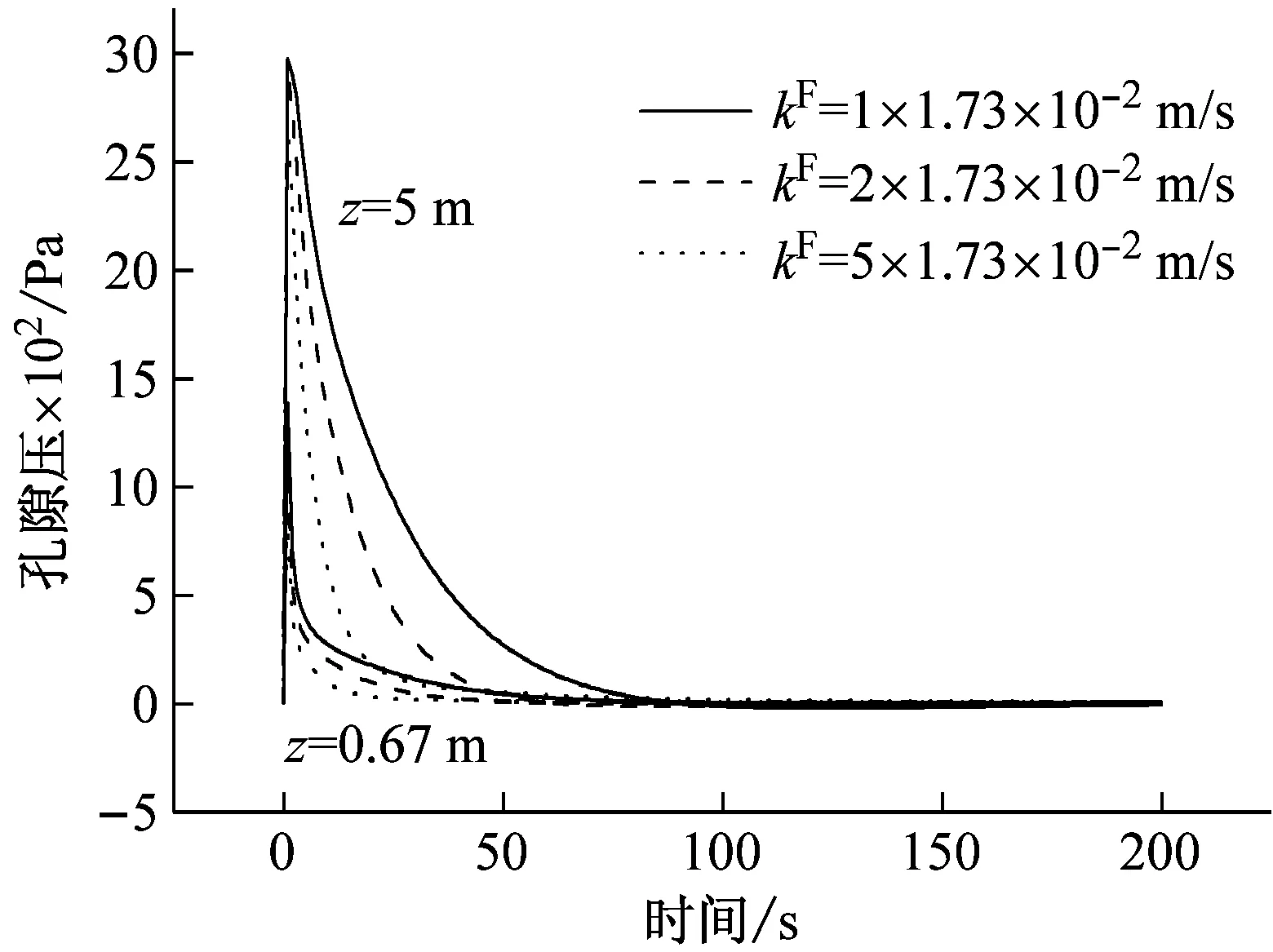
(c) 孔隙压

(d) 温度图7 阶梯温度载荷作用下柱体的时-程曲线Fig.7 Time-history curves of the cylinder under the step temperature loading

同时，本文考虑了热交换系数β，热传导系数k等对柱体的影响。结果表明，热交换系数β越小，流固两相之间相互作用力越小，初始阶段固相的热体积膨胀效应被抑制，柱体沉降较大。而当热传导系数k较大时，温度场达到稳态所需时间短，初始阶段热传导过程快于固结作用过程，柱体沉降较小。

(2) 在循环温度载荷和外载荷情况下的结果

图8中给出了在循环温度载荷和外载荷作用下，达西渗透系数κF对对称轴不同深度处的沉降uz，相对流速wz，孔隙压p及温度变化θ的影响。计算表明，在循环温度载荷下，柱体的热动力学整体性质和在阶梯温度载荷下相似，除了时-程曲线呈周期性变化外。达西渗透系数κF较小时，热传导过程快于机械载荷下的固结作用过程，初始阶段表现为柱体固相的热体积膨胀效应，沉降的振幅小。

同时，热交换系数β越小，流固两相之间相互作用力越小，初始阶段固相的热体积膨胀效应被抑制，柱体沉降大。而当热传导系数k较大时，温度场达到稳态所需时间短，初始阶段热传导过程快于固结作用过程，柱体沉降小。

在所考虑的几种情况下，柱体温度随时间的增大周期性变化，并由上表面向纵深处传导和扩散，各物理量沿纵深方向存在相位差，但周期相同。

(a) 沉降

(b) 相对流速

(c) 孔隙压

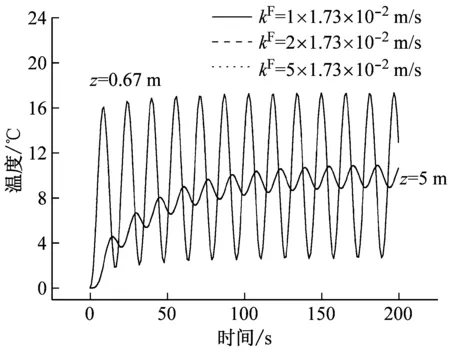
(d) 温度图8 循环温度载荷作用下柱体的时-程曲线Fig.8 Time-history curves of the cylinder under the cycle temperature loading

4 结 论

本文基于de Boer多孔介质混合物理论，综合采用DQM-二阶向后差分法-Newton-Raphson迭代法，研究了空间轴对称流体饱和多孔热弹性柱体在表面温度载荷作用下的动力学特性。

为了验证本文方法的正确性，计算了无热效应时不可压流体饱和多孔弹性柱体的动力固结问题，并与现有解析结果进行了比较，二者吻合良好，证明DQM具有精度高，计算量小，数值稳定等优点。

本文分别研究了空间轴对称流体饱和多孔热弹性柱体在热局部平衡条件下，只受到表面外载荷作用下的动力学特性和受到表面温度载荷与外载荷联合作用下的动力学特性，并比较了在柱体上表面给定两种不同温度载荷(即阶梯温度载荷和周期温度载荷)的结果，考察了材料的某些参数对柱体动力学特性的影响。结果表明在两种温度载荷的作用下，除了在周期温度载荷条件下柱体物理量的时-程曲线呈周期性变化外，柱体的热动力学整体特性是相似的：随着时间的增加，柱体沉降趋于稳定、流速逐渐趋于零、孔隙压由初始值逐渐消散至零、温度逐渐上升并由上表面向纵深处传导和扩散；同时，当达西渗透系数κF较大或热交换系数β较小时，初始阶段柱体固结作用过程快于热传导过程，柱体沉降大；当热传导系数k较大时，温度场达到稳态所需时间短，初始阶段热传导过程快于固结作用过程，柱体沉降较小。另外，在周期温度载荷作用下，柱体温度随时间的增大周期性变化，并由上表面向纵深处传导和扩散，各物理量沿纵深方向存在相位差，但周期相同。

[1] BIOT M A. Theory of elasticity and consolidation for a porous anisotropic solid[J]. Journal of Applied Physics, 1955, 26(2): 182-185.

[2] CUI Y J, SULTAN N, DELAGE P. A thermomechanical model for saturated clays[J]. Canadian Geotechnical Journal, 2000, 37(3): 607-620.

[3] WU W H,LI X K,CHARLIER R, et al. A thermo-hydro-mechanical constitutive model and its numerical modeling for unsaturated soils[J]. Computers & Geotechnics, 2004, 31(2): 155-167.

[4] 刘干斌, 姚海林, 杨洋, 等. 考虑热-水-力耦合效应多孔弹性地基的动力响应[J]. 岩土力学, 2007, 28(9): 1784-1795.

LIU Ganbin, YAO Hailin, YANG yang, et al. Coupling thermo-hydro-mechanical dynamic response of a porous elastic medium[J]. Rock and Soil Mechanics, 2007, 28(9): 1784-1795.

[5] 白冰. 循环温度荷载作用下饱和多孔介质热-水-力耦合响应[J]. 工程力学, 2007, 24(5): 87-92.

BAI Bing. Thermo-hydro-mechanical responses of saturated porous media under cycle thermal loading[J]. Engineering Mechanics, 2007, 24(5): 87-92.

[6] DE BOER R. Theoretical poroelasticity-a new approach[J]. Chaos Solitons & Fractals, 2005, 25(4): 861-878.

[7] BOWEN R M. Compressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1982, 20(6): 693-735.

[8] SCHREFLER B A. Mechanics and thermodynamics of saturated /unsaturated porous materials and quantitative solution[J]. Applied Mechanics Reviews, 2002, 55(4): 351-388.

[9] PLACIDI L, DELL’LSOLA F, IANIRO N, et al. Variational formulation of pre-stressed solid-fluid mixture theory, with an application to wave phenomena[J]. European Journal of Mechanics A/Solids, 2007, 27(4): 582-606.

[10] DE BOER R, EHLERS W, LIU Z. One-dimensional transient wave propagation in fluid-saturated incompressible porous media[J]. Archive of Applied Mechanics, 1993, 63(1): 59-72.

[11] HEIDER Y, MARKERT B, EHLERS W. Dynamic wave propagation in infinite saturated porous media half spaces[J]. Computational Mechanics, 2012, 49(3): 319-336.

[12] HU Y J, ZHU Y Y, CHENG C J. DQM for dynamic response of fluid-saturated visco-elastic porous media[J]. International Journal of Solids & Structures, 2009, 46(7): 1667-1675.

[13] DE BOER R, KOWALSKI S J. Thermodynamics of fluid-saturated porous media with a phase change[J]. Acta Mechanica, 1995, 109(1): 167-189.

[14] HE L W, JIN Z H. A local thermal non-equilibrium poroelastic theory for fluid saturated[J]. Journal of Thermal Stresses, 2009, 33(8): 799-813.

[15] YANG X. Gurtin-type variational principles for dynamics of a non-local thermal equilibrium saturated porous medium[J]. Acta Mechanica Solida Sinica, 2005, 18(1): 37-45.

[16] QIN B, CHEN Z H, FANG Z D, et al. Analysis of coupled thermo-hydro-mechanical behavior of unsaturated soils based on theory of mixtures I[J]. Applied Mathematics and Mechanics (English Edition), 2010, 31(12): 1561-1576.

[17] EHLERS W, HBERLE K. Interfacial mass transfer during gas-liquid phase change in deformable porous media with heat transfer[J]. Transport in Porous Media, 2016, 114(2): 1-32.

[18] BELLMAN R E, CASTI J. Differential quadrature and long term integration[J]. Journal of Mathematical Analysis & Applications, 1970, 34(2): 235-238.

[19] BELLMAM R E, KASHEF B G, CASTI J. Differential quadrature: a technique for the rapid solution of nonlinear partial differential equations[J]. Journal of Computational Physics, 1972, 10(1): 40-52.

[20] BERT C W, MALIK M. Differential quadrature method in computational mechanics: a review[J]. Applied Mechanics Reviews, 1996, 49(1): 1-28.

[21] CHEN C N. The two-dimensional frames model of the dfferential quadrature element method[J]. Computers & Structures, 1997, 62(3):555-571.

[22] ZHU Y Y, LI Y, CHENG C J. Analysis of nonlinear characteristics for thermoelastic half-plane with voids[J]. Journal of Thermal Stresses, 2014, 37(7): 794-816.

Dynamiccharacteristicsforaspatial-axisymmetricfluid-saturatedporousthermo-elasticcylinderbasedonDQM

ZHU Yuanyuan1, HU Yujia2, CHENG Changjun3, ZHENG Xiaomei1

(1. College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China；2. College of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China;3. Department of Mechanics, Shanghai University, Shanghai 200072, China)

Dynamic characteristics of an incompressible spatial-axisymmetric fluid-saturated porous thermo-elastic cylinder subjected to a surface temperature loading were studied in case of local thermal equilibrium. Firstly, the mathematical model of the problem was established based on de Boer porous media theory. Then, the differential quadrature method, the second-order backward difference scheme and Newton-Raphson iterative method were synthetically used to solve the mathematical model and obtain the numerical results of the unknown quantities at every discretized point, and the dynamic characteristics of the cylinder were further studied. In order to verify the validity of the proposed method, the dynamic consolidation problem of an incompressible fluid-saturated porous elastic cylinder was computed with this method. The obtained numerical results agreed well with the analytical ones published by de Boer et.al, it was shown that the proposed method has two advantages: smaller amount of computation and higher accuracy. Finally, the dynamic characteristics of a spatial-axisymmetric fluid-saturated porous thermo-elastic cylinder subjected to mechanical load or both mechanical load and temperature load were studied and compared, the effects of material’s some parameters on the dynamic characteristics of the cylinder were investigated.

fluid-saturated porous thermo-elastic cylinder； porous media theory(PMT)； spatial-axisymmetric problem； differential quadrature method (DQM)； thermo-dynamic

上海市自然科学基金(15ZR1431600)

2017-01-13 修改稿收到日期：2017-04-06

朱媛媛 女，博士，副教授，1971年3月生

胡育佳 男，博士，副教授，1979年3月生

TU311

A

10.13465/j.cnki.jvs.2017.23.013