浅谈全国卷背景下数学通性通法的教学

文梅县东山中学 廖宗云

浅谈全国卷背景下数学通性通法的教学

文梅县东山中学 廖宗云

纵观近几年全国新课标卷和大纲卷的数学所有考题，从内容到形式，尽管它们精彩纷呈，各有特色，但唯一共同的特点是对通性通法的考查力度均占绝对的比例优势。所以全国卷下我们中学数学的教学应该是注重数学思想和数学基本方法的培养，但是在实际教学中，我们往往跑偏了，喜欢追求花哨的特殊解题技巧，喜欢让学生接触一些华丽的所谓“压轴题”和“好题”，而忽视了通性通法的培养。

所谓通性通法，是指具有某些规律性和普遍意义的常规解题模式和常用的数学思想方法。近几年来一直是高考考查的核心，因而在日常教学中我们一定要重视数学思想方法的渗透，让学生切实领悟数学思想方法的实质，会用数学思想方法解决问题。在新课程中强化通性通法教学，淡化特殊技巧用于的要求，因此高中数学新课程中，删减了烦琐的计算，淡化了人为技巧化的难题，突出对分析、解决问题能力的要求。现在高考比较重视的就是这种具有普遍意义的方法和相关的知识。

一、紧扣新课标和考试大纲，避开怪难偏

在教学过程中，应该以新课标为准线，吃准和吃透新课标的要求，不要盲目地追求课堂的标新立异，在高三的复习中，更是要深入研读考纲，避免出现超纲的教学内容。例如，在函数的教学，新课标就提出“在教学中，应强调对函数概念本质的理解，避免在求函数定义域、值域及讨论函数性质时出现过于烦琐的技巧训练，避免人为地编制一些求定义域和值域的偏题”。又如在推理与证明的复习，大纲明确提出“本模块（指推理与证明）中设置的证明是对学生已学过的基本证明方法的总结。在教学中，应通过实例，引导学生认识各种证明方法的特点，体会证明的必要性。对证明的技巧性不宜作过高的要求。”

二、结合学生实际，优化教学内容

在以往的教学中对于一些特殊技巧解答问题提出过一定的要求，但是这类题目学生得分率较低。技巧性问题难度大，应用面窄，适合于数学竞赛，并不适合用于高考。对于特殊技巧，如果老师不补充或学生在课外作业中未见过做过，想在考场这一特定环境内解答出来是不可能的，如果在高考试题中常出现特殊技巧性问题，必定引起教师补充讲授各种解题技巧及技巧性强的题目，加重教师和学生的负担，导致题海战术；另一方面，由于信息社会要求我们具有较高的数学素养，科学技术的发展降低了对数学技巧的要求，综合上述原因，“淡化特技”成为高考数学命题的必然选择。这就要求我们在授课的时候，要优化教学内容，结合学生的实际，选择适合学生实际的解题方法。笔者在一次公开课听课接触过一个例子：

例1.二次函数f(x)=ax2+bx+c的图象经过点（-1，0），是否存在常数a,b,c使不等式x≤f(x)≤对一切实数都成立？若存在，求出a,b,c；若不存在，说明理由。

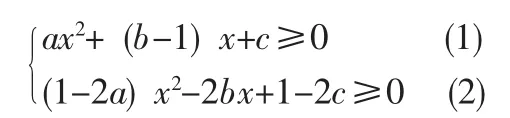
学生自然而然想到了一元二次不等式恒成立的充要条件，当时1-2a=0时，f(x)不存在。

结合图像过点（-1，0），列出不等式组

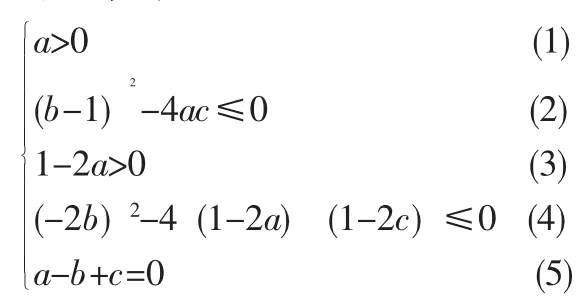
怎样求出a,b,c？学生思维阻塞，困惑得很，此时，教师只需作适当点拨，碰到多变量的问题，要如何处理？学生回答：减少变量。用什么方法减少变量呢？学生通过试验，感到消去a、消去c都很困难，必须消去b，将代入b=a+（2）、（4）式分别得(a-c)2-2(a+c)+1≤0（6），(a-c)2+2(a+c)-1≤0（7）。

此时，许多学生又茫茫然不知所措，（6）、（7）式有何作用？教师继续点拨，观察（6）、（7）两式的结构特征，你会将它们如何变形？学生恍然大悟，由（6）+（7）得(a-c)2，∴a=c。这样，就把（6）、（7）两式中隐含的相等关系挖掘出来（能挖掘隐含条件是思维深刻性的具体表现）。将a=c代入（6）、（7）式可得到4a-1≥0,4a-1≤0,故存在使不等式对一切实数x都成立。

这样解题，思路自然贴切，比较适合学生的思维方式。而在听课过程中却发现，授课教师在一开始就采用了巧解的方式：

这种解法，巧妙得令人惊叹，但有谁会立即想到不等式链（*）呢？况且不等式链（*）仅在习题中出现，学生很陌生，这样的解法是怎样想到的？学生自感茫然。在这道题上，不妨在讲完通法后，再由通法引入巧解。

三、突出基础知识，加大对典型题的训练力度

尽管当前高考数学试卷不再刻意追求知识点的覆盖面，但凡是《考试说明》中规定的知识点，在复习时一个都不能遗漏。况且，某个知识点，连续几年不考的概率很小。从全国卷历年的高考试题中可以发现，高考试题几乎都是以函数、三角函数、数列、不等式、圆锥曲线、空间线面关系及其计算、概率统计这几个主干知识点为中心展开的，高考命题体现“对重点知识的考查要保持较高的比例，并达到必要的深度”这一命题思想是永远也不会改变的。

现在的全国卷数学试题中大部分都是中档题，而中档题又大多是基础题的加深、综合或拓展。主要考查数学的基本概念、基本知识和基本的计算解题方法，所以平常的复习，必须扎根于课本，回到基础上去，对课本中的概念、法则、性质、定理、公理、公式等进行梳理，要理清知识发生的本原(如等差数列、等比数列求和公式的推导过程等)，考生要注意从学科整体意义上建构知识网络，形成完整的知识体系，掌握知识之间内在联系与规律，重点放在掌握典型例题涵盖的知识及解题方法上。

我们在教学过程中要引导学生对这些普遍性的东西不断地进行概括总结，不断地在具体解题中细心体会，千万不要去刻意追求一些解题的特殊技巧，尽管一些数学题目有多种解法，有的甚至有十几种解法，但这些解法中具有普遍意义的通用解法也就一两种而已。我们要更多地注重思考题目的“核心”是什么，从题目中“提炼”反映数学本质的东西，掌握好数学模式题的通用方法。

只有当我们的教学做到返璞归真，还原本质，注重了“源”与“本”的关系，加强对通性通法的认可和掌握，才能提高学生对“双基”的灵活运用，我们的教学才能不跑偏，真正提高学生的数学素养，在全国卷下数学能力的全面考查中显得更加从容。

责任编辑 韦英哲