风电接入位置对系统暂态稳定性的影响分析

张 师，于锡平，秦英炜，王睿奇，陈立铭，周立新

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.国网吉林省电力有限公司检修公司，吉林 长春 130000；3.吉林吉电集团有限公司，吉林 吉林 132001;4.广东电网有限公司湛江供电局，广东 湛江 524000)

风电接入位置对系统暂态稳定性的影响分析

张 师1，于锡平2，秦英炜3，王睿奇4，陈立铭1，周立新1

(1.东北电力大学电气工程学院，吉林 吉林 132012；2.国网吉林省电力有限公司检修公司，吉林 长春 130000；3.吉林吉电集团有限公司，吉林 吉林 132001;4.广东电网有限公司湛江供电局，广东 湛江 524000)

随着风电并网容量逐渐增加，风电对系统暂态稳定性的影响不容忽视，风电接入位置对受扰后的同步机动态行为具有重要影响。为研究风电接入位置对电力系统暂态稳定的影响机理，采用扩展等面积法则，分析了风电接入对临界机组和余下机组电磁功率波动的影响，得出风电接入位置对系统暂态稳定性的影响。通过分析可知，当受扰后风电机组附近的同步机为临界机组时，风电接入会恶化系统暂态稳定；当受扰后风电机组附近的同步机为余下机组时，风电接入会有利于暂态稳定。

风电机组；扩展等面积法则；临界机组

0 引言

我国可再生能源“十三五”发展规划指出：预计2020年我国非化石能源占能源消费比例15%，2030年非化石能源占能源消费比例20%。风力发电作为技术最成熟的清洁能源在近几年得到迅猛发展[1-4]，与此同时，大规模风电并网对系统暂态稳定的影响也得到了学者们的广泛关注。

文献[5]仿真分析了不同类型风电机组对电力系统暂态稳定性的影响，并得出结论双馈风电机组(double fed integration generator，DFIG)并网对系统暂态稳定最有利。文献[6]分析了暂态过程中DFIG轴系模型对系统动态行为的影响。通过分析可知，暂态过程中轴刚度越低，转子因轴松弛而获得的预期加速越多，越不利于系统暂态稳定。文献[7]通过仿真算例发现：额定风速下风电场接入电网的绝对安全容量是有限的，而风速较低时，风电场可以开启更多的风电机组来提高风电场的出力。文献[8]以实测运行数据为基础，通过分析得出近满载工况下的DFIG由于转子电流裕度较低，更容易发生连锁脱网事件。文献[9]分析了不同运行工况下的DFIG对电力系统暂态稳定性的影响。

以上研究中，未见风电接入位置对系统暂态稳定的影响研究，因此本文基于扩展等面积法则分析风电并网位置对系统暂态稳定的影响。

1 扩展等面积法则基本原理

扩展等面积法则(extended equal area criterion，EEAC)是由薛禹胜首次提出，将等面积法则应用于多机系统的暂态稳定性分析中[10-15]。

设具有n台同步发电机系统，第i台同步机的功角δi变化与功率差额的关系可以表示为

(1)

式中：Mi为第i台同步机的惯性时间常数；PMi和PEi为第i台同步机的机械功率和电磁功率。

惯性中心(center of inertia，COI)的功角和转速为：

式中：δCOI和ωCOI分别为惯性中心的功角和转速。

COI坐标下的各台发电机转子运动方程为

(4)

式中：PCOI为各台发电机的功率差额总和；MΣ为各台发电机的惯量加和。将相对于COI加速的和减速的发电机群分别定义为临界群和余下群，临界机组为受扰后加速较快的机组，余下机组未受扰后加速较慢的机组。n台发电机有nk台临界机组，则等值临界机组和余下机组的功角δk和δ0可以表示为：

等值临界机组和余下机组的转子运动方程为：

式中：Mi和Mj分别为等值临界机组和余下机组的转动惯量；PMi-PEi为临界机组的功率差额；PMj-PEj为余下机组的功率差额。

将式(7)(8)联立可得

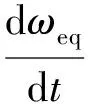
(9)

等值惯量Meq、等值机械功率PMeq和等值电磁功率PEeq可以表示为：

等值系统的加速面积和减速面积为：

式中：PEeqⅡ为故障过程中的电磁功率；PEeqⅢ为故障清除后的电磁功率；δ0、δc和δh分别为初始功角、故障切除时功角和不稳定平衡点的功角。加速面积越小、减速面积越大，越有利于提高系统的暂态稳定性。

2 风电并网位置对系统暂态稳定性的影响

为便于分析，以等值两机系统为例，系统如图1所示。

图1 两机系统示意图Fig.1 Schematic diagram of two machine system

当系统发生短路故障后，Syn1和Syn2必然相对摆开，两机的功角摆动取决于各自转动惯量、扰动位置及扰动大小，受扰后2台发电机的功角波动不同，必然会有1台临界机组和1台余下机组。图1系统中bus1与bus2的传输功率极限为

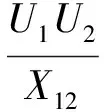
(15)

式中：U1和U2分别bus1和bus2的电压；X12为bus1和bus2间电抗。动态过程中系统各节点电压会波动，bus1-bus2的功率传输极限也在波动，当风电接入后，在影响U1和U2波动的同时，风电输出的功率也会使同步机的输出功率减小。

等值系统机械功率由扰动前的各台发电机工况决定，根据式(12)可知，当风电机组并网后可以减小余下机组的电磁功率时，等值系统电磁功率将增大，从而减小等值系统功率差额，提高系统暂态稳定性；当风电机组并网后可以减小临界机组的电磁功率时，等值系统电磁功率将减小，从而增加系统功率差额，恶化系统暂态稳定性。

通过以上分析可知，风电并网对系统暂态稳定性的影响取决于风电机组的接入位置。

3 算例分析

本文采用Matlab工具箱PSAT仿真分析，如图2为采用PSAT搭建的3机9节点系统，系统中各元件参数参见文献[15]。

图2 3机9节点系统Fig.2 3 machine 9 node system

100 MW满载工况的DFIG分别接入bus4和bus9，在bus5增加100 MW负荷，设置1 s时在bus6-bus7靠近bus7一侧发生三相短路，在1.05 s时该线路被切除，故障清除，采用变步长积分，仿真时间10 s，基准功率100 MVA。

仿真结果如图3所示。原系统中Syn3为余下机组，Syn1和Syn2为临界机组。Syn1接入位置为bus2，Syn2接入位置为bus3，Syn3接入的位置为bus1。当DFIG接入bus4时，靠近Syn3，各台发电机在暂态过程中可以保持同步运行，不发生非周期性失步，且各台发电机功角波动幅度较原系统比有所减小；当DFIG接入bus9时，靠近Syn2，在6 s各台发电机功角相对摆开，系统失稳。

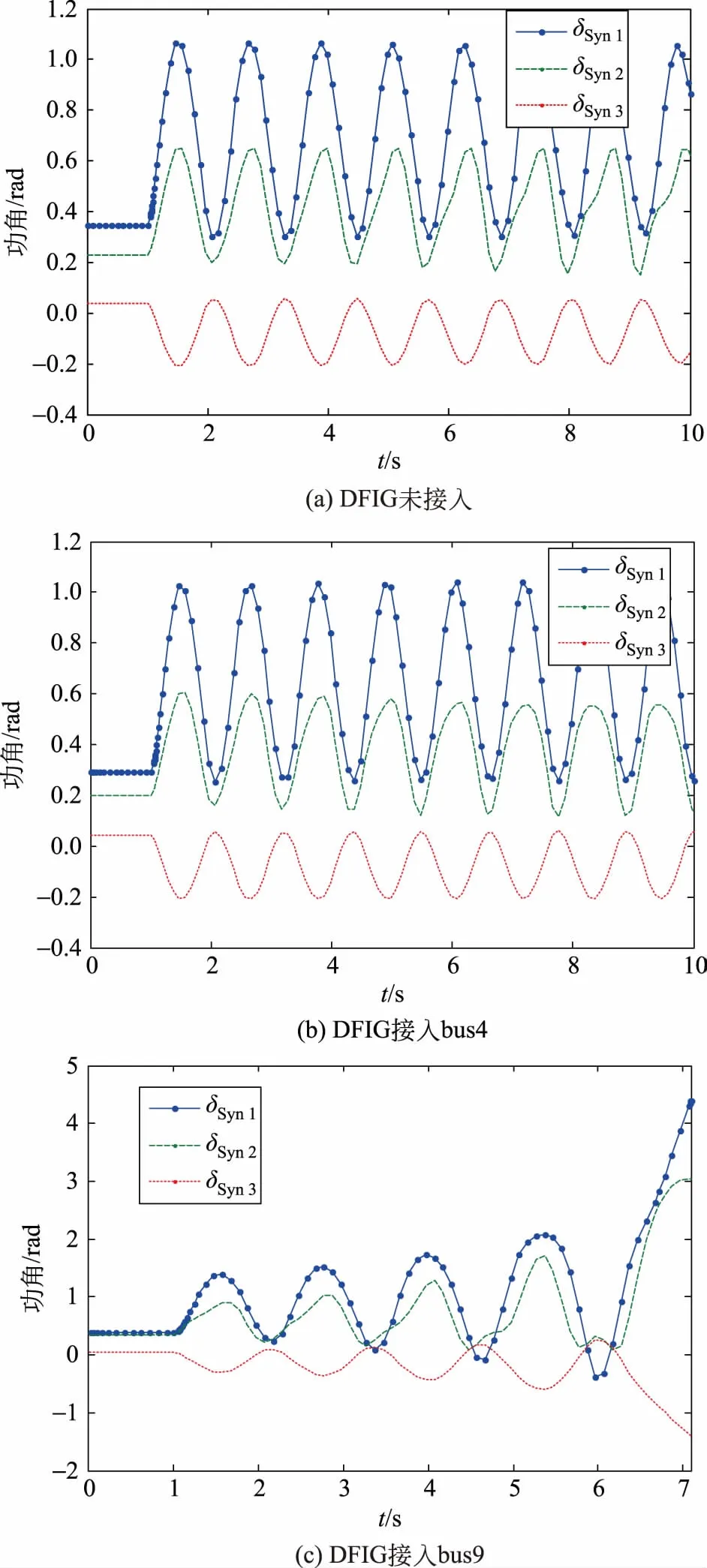
图3 DFIG接入前后的仿真曲线Fig.3 Simulation curve before and after DFIG access

通过以上分析可知，风电机组接入系统后对系统的暂态稳定影响取决于风电机组接入的位置，当受扰后风电机组附近的同步机为临界机组时，风电功率会占用临界机组的功率输送通道，降低临界机组的电磁功率，从而加重临界机组和余下机组的相对摆开，恶化系统暂态稳定；当受扰后风电机组附近的同步机为余下机组时，风电功率会占用余下机组的功率输送通道，降低余下机组的电磁功率，增加余下机组的功角增量，缓解临界机组和余下机组的相对摆开，有利于暂态稳定。

4 结论

本文基于EEAC分析了风电接入位置对系统暂态稳定性的影响，通过本文分析可知，风电接入对系统暂态稳定的影响取决于风电接入位置。当受扰后风电机组附近的同步机为临界机组时，风电接入会恶化系统暂态稳定；当受扰后风电机组附近的同步机为余下机组时，风电接入会有利于暂态稳定。

[2] MEHTA B, BHATT P, PANDYA V. Small signal stability analysis of power systems with DFIG based wind power penetration[J]. International Journal of Electrical Power & Energy Systems, 2014, 58(6): 64-74.

[3] ROY S M, BHATTI T S, VERMA A. Effect of DC link discharge resistor on transient stability of DFIG wind generator[C]//IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems. IEEE, 2017:1-4.

[4] WU B, LANG Y, ZARGARI N, et al. Power conversion and control of wind energy systems[M]. IEEE Press, Wiley, 2011.

[5] 申洪. 变速恒频风电机组并网运行模型研究及其应用[D]. 北京： 中国电力科学研究院， 2003.

SHEN Hong. Studies on integrated variable-speed constant-frequency wind turbine models and the application[D]. Beijing: China Electric Power Research Institute, 2003.

[6] 郝元钊. 风力发电机组对电网稳定性影响的研究[D]. 长沙： 湖南大学， 2011.

HAO Yuanzhao. Research on power system stability of wind plant to power grid[D]. Changsha: Hunan University, 2011.

[7] 张红光，张粒子，陈树勇，等.大容量风电场接入电网的暂态稳定特性和调度对策研究[J].中国电机工程学报， 2007， 27(31)： 45-51.

ZHANG Hongguang， ZHANG Lizi， CHEN Shuyong， et al. Studies on the transient behavior and dispatching strategy of power system integrated with large scale wind farms[J]. Proceedings of The CSEE， 2007， 27(31)： 45-51.

[8] 穆钢， 王健， 严干贵， 等. 双馈型风电机群近满载工况连锁脱网事件分析[J]. 电力系统自动化， 2011, 35(22)： 35-40.

MU Gang， WANG Jian， YAN Gangui，et al. Cascading trip-

off of doubly-fed induction generators from grid at near full-load condition in a wind farm[J]. Automation of Electric Power Systems， 2011， 35(22)： 35-40.

[9] 安军, 张师, 穆钢,等. 双馈风电场有功分配方式对风火打捆系统暂态稳定性的影响[J]. 太阳能学报, 2017, 38(5): 1391-1396.

AN Jun, ZHANG Shi, MU Gang, et al. The study of DFIG wind farm real power dispatching mode influence on the transient stability of wind-thermal bundled power system[J]. Acta Energiae Solaris Sinica, 2017, 38(5):1391-1396.

[10] LIU Z, LIU C, LI G, et al. Impact study of PMSG-based wind power penetration on power system transient stability using EEAC theory[J]. Energies, 2015, 8(12): 13419-13441.

[11] ZHOU H, GUO J, JU P. Quasi hamilton system stochastic averaging and EEAC combined transient stability analysis method[C]//International Conference on Probabilistic Methods Applied To Power Systems. IEEE, 2016: 1-5.

[12] CAI Z, SHEN H, WANG L. FACTS modeling for transient stability analysis based on EEAC[J]. Automation of Electric Power Systems, 2000.

[13] MUKNAHALLIPATNA S, LEGOWSKI S, ULA S, et al. Power system transient stability analysis software tool for an undergraduate curriculum[J]. Computer Applications in Engineering Education, 2001, 9(1): 37-48.

[14] QIAN F, TANG G, HE Z. Optimal location and capability of FACTS devices in a power system by means of sensitivity analysis and EEAC[C]//International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. IEEE, 2008: 2100-2104.

[15] MILANO F. An open source power system analysis toolbox[J]. IEEE Transactions on Power Systems, 2005, 20(3): 1199-1206.

InfluenceofWindPowerAccessLocationonSystemTransientStability

ZHANG Shi1, YU Xiping2, Qin Yingwei3, WANG Ruiqi4, CHEN Liming1, ZHOU Lixin1

(1. School of Electrical Engineering, Northeast Electrical Power University, Jilin 132012, Jilin Province, China; 2. Maintenance Company of State Grid Jilin Electric Power Company, Changchun 130000, Jilin Province, China; 3. Jilin Jidian Power Group Co., Ltd., Jilin 132001, Jilin Province, China; 4. Zhanjiang Power Supply Bureau, Guangdong Power Grid Co., Ltd., Zhanjiang 524000, Guangdong Province, China)

With the increasing capacity of wind power grid, the influence of wind power on system transient stability cannot be ignored; the wind power access location has an important influence on the dynamic behavior of synchronous machine after disturbance. For the study of wind power access location influence mechanism on the transient stability of power system, this paper uses the extended equal area criterion to analyze the impact of wind power access on the electromagnetic power fluctuations of critical units and the remaining units, and obtains the impact of wind power access location on the transient stability of the system. The analysis results show that, when the synchronous machine near the disturbance of wind turbine is critical unit, wind power will deteriorate the system transient stability; when the synchronous machine near the disturbance of wind turbine is remaining unit, wind power is beneficial to transient stability.

wind turbines; extended equal area criterion; critical units

TK 01；TM 71

A

2096-2185(2017)06-0078-04

10.16513/j.cnki.10-1427/tk.2017.06.013

张 师

张 师(1989—)，男，硕士，助理实验师，研究方向为电力系统动态安全分析，zs472254835@126.com；

于锡平(1967—)，男，学士，工程师，研究方向为电力系统稳定与控制；

秦英炜(1983—)，男，工程硕士，工程师，研究方向为风电并网系统稳定性研究；

王睿奇(1994—)，男，学士，研究方向为电力系统功角稳定性研究；

陈立铭(1993—)，男，硕士研究生，研究方向为电力系统稳定性分析；

周立新(1994—)，男，本科生，研究方向为电力系统动态安全分析。

2017-09-19

(编辑 蒋毅恒)