银行间市场中信用事件风险传染分析
——基于银行主体信用评级变化的风险传染建模研究
吴 亮,庄亚明,赵 磊
(1东南大学 经济管理学院,江苏 南京 211189; 2河南科技学院 数学科学学院,河南 新乡 453003)
银行间市场中信用事件风险传染分析
——基于银行主体信用评级变化的风险传染建模研究
吴 亮1,2,庄亚明1,赵 磊2
(1东南大学 经济管理学院,江苏 南京 211189;2河南科技学院 数学科学学院,河南 新乡 453003)
银行间市场由于银行主体之间通过信用借贷,形成了一种复杂的信用关系网。当银行间市场受到宏观经济或突发性事件影响时,银行主体的信用评级可能会产生移动,即单个银行的信用评级可能升高或降低,甚至信用破产,进而引发信用风险在银行间市场的扩散和传染。因此,有必要对基于银行主体信用评级变动所产生的风险传染的路径和强度进行深入研究。本文构建了用于分析银行间市场中信用评级变化的带自激过程的强度模型,并根据稀疏相关性理论,给出了具有评级变化相关性的两个银行的联合信用安全概率。
信用评级变化;风险强度模型;稀疏相关性
一、引 言
银行间市场是由同业拆借市场、债券市场、外汇市场、黄金市场、票据市场等构成。银行间市场有着货币供应、调节货币流通、调节银行之间的货币余缺以及金融机构货币保值增值等作用。因此,银行间市场的稳定运行对整个金融市场,甚至整个国民经济的稳定发展都起着“基石”的重要作用。另一方面,中国银行间市场的成员和规模都在快速增加,同时交易方式和使用工具也愈加灵活多样,使得银行个体之间通过信用借贷形成了一种复杂的信用关系网络结构。
银行信用评级(Bank’s Credit Rating)是对单个银行目前偿还其债务的金融能力的评价,它对于投资者评估、回避风险,对银行业者扩大筹资途径、稳定资金来源,对监管者提高监管效率,降低市场运行的不稳定性,都有着很重要的意义。然而,当银行间市场受到宏观经济或突发性事件的影响时,银行主体的信用评级可能会产生移动,即单个银行的信用评级可能升高或降低,甚至出现银行信用违约、破产,这些信用评级变动都是银行间市场的信用事件。
银行间市场的信用事件风险传染是指单个银行的信用评级发生移动时对其他银行信用评级产生的影响。在银行间市场中,银行业者通过信用拆借关系交织在一起。当银行间市场中有一个银行主体受冲击而产生银行信用评级移动时,这一冲击可能通过信用链关系网传递给其他银行,并给其他银行带来信用评级调整的风险,进而这种风险可能在整个银行间市场中交织扩散,导致整个银行间市场的系统性危机,造成银行业者严重的经济损失,乃至影响整个实体经济的健康发展,即信用事件引发信用风险在银行间市场的扩散和传染。诸如2007年爆发的美国次级贷款危机,2010年爆发的欧洲主权债务危机等,都使得银行间市场中不少银行主体信用评级产生变化,甚至出现银行倒闭、清算。因此,有必要对基于银行信用评级变动所产生的信用事件风险在银行间市场中传染、扩散的路径和强度进行深入研究,揭示信用事件风险传染的内在关系,为提升银行间市场的稳定运行、防范金融危机提供一定的理论方法。
二、文献综述
现有关于信用事件风险传染的研究,主要集中在信用违约事件的风险传染分析方面,并根据风险模型的类型分为结构模型、约化模型和混合模型。结构模型将违约事件视为一种内生变量,与公司(银行)的资产价值相关,并利用公司(银行)的资产价值及负债信息建立模型。结构模型首先由Merton[1]提出,其主要思想是将期权定价的理论用于信用衍生品的定价。后来,许多学者基于结构模型的思想提出了不同的改进模型,如Kou和Wang[2]、Kou, Petrella和Wang[3]等。但结构模型的不足之处是对违约的不可预见性考虑不足。约化模型认为公司(银行)的资产价值时常是不可观测的,所以认为违约事件是由外生变量决定的,不可预料的。相比结构模型,约化模型在现实市场中显得更灵活。约化模型由Fons J S[4]首次提出,其发现信用价差依赖于发行人的信用评级变化,此约化模型结构虽简单,但模型运行结果与现实市场数据很接近。从此各种约化模型开始不断出现[5-7]。约化模型的主要缺点是被模型视为外生的违约机制缺乏解释力,且对历史数据要求高。基于结构模型和约化模型各自的不足及它们内在的联系,有学者力图将结构化方法和约化方法结合。利用不同的信息集将结构模型中的违约可料性减弱,进而引入违约强度,建立了一种同时能表明模型的经济背景又不过于复杂的混合模型[8-9]。
现实经济市场中信用事件风险却不单单指违约事件造成的风险,由于银行或其他经济实体的信用评级的变化,如银行信用评级的降低或升高,都可能对其他的银行或经济实体产生或负或正的影响,即信用事件产生的风险进行了传染和扩散。因此,有必要对由于经济实体的信用评级的升高、降低、乃至信用违约等所有信用事件产生的风险传染和扩散进行全面分析。Nakagawa[10-11]基于上下方法(top-down approach)为信用评级变化(包括信用评级升高、降低和信用违约)构造了一个带有自激(self-exciting)过程的强度模型,该模型能对所有类型的信用事件风险传染过程进行模拟分析。在通常的信用评级变化模型中都需要一个评级移动(rating transition)强度矩阵来模拟信用评级的变化,然而想利用这样一个评级移动强度矩阵为某一金融部门或投资组合的动态相依的风险进行分析是很困难的,但是利用Nakagawa提出的信用变化强度模型,在处理动态相依的风险时便不会出现上述困难。Giesecke[12],Yamanaka[13]各自为整个经济市场中的信用事件构造了一种状态相依自激的强度过程。该类模型考虑了整个市场中的信用事件,且有自我激励的强度,所以能捕捉到经济市场中经济实体信用质量的变化过程和不同经济实体间信用风险的相依性。
银行间市场的稳定运行关系到整个经济的健康发展,然而银行间市场会时常受到来自宏观经济环境、突发性事件或是银行自身营运状况的影响,产生信用评级的变化,出现信用事件,进而出现信用事件风险在银行间市场中的传染和扩散[14-15]。由上述分析,有必要基于银行间市场中银行个体信用评级的变化,为信用事件风险的传染建立风险预警模型。据现有文献所知,目前国内尚没有关于此问题的风险模型,本文对此做出了探索性的研究。受Nakagawa、Giesecke和Yamanaka模型的启发[10-13],基于银行个体信用评级的变化,构建用于分析银行间市场中信用评级变化的带自激过程的强度模型,并根据稀疏相关性理论,给出具有评级变化相关性的两个银行的联合信用安全(信用安全指没有发生信用评级变化)概率。需要说明的是,本文的风险模型是在Nakagawa和Yamanaka模型的基础上得到的,但同他们的模型在信用变化跳跃大小及评级移动的条件概率等方面完全不同。
三、信用评级变化的风险模型
本文对信用评级变化和信用违约风险传染的建模是基于带自激强度过程的点过程。这一部分主要针对银行间市场中的每一个类型的信用事件构造一种点过程风险预警模型,且根据银行信用评级变化的分布指定出模型的随机细化过程。
(一)信用变化的强度模型
在银行间市场中,假设每一个银行实体被赋予了一个信用评级,这里共分为K+1等评级。评级具体用1,2,…,K和K+1表示,并且评级的顺序代表了信用质量,即k=1代表最高的信用质量,k=K表示最差的非违约的信用质量,而k=K+1则代表信用违约状态。
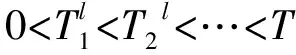
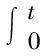
(1)
(2)
(3)
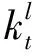
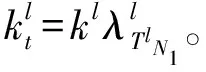
由于上述跳跃大小的表达式都有求和过程,致使它们可能出现跳跃大小无界的现象,在应用Giesecke和Yamanaka强度模型进行信用评级变化模拟仿真时,可能产生不现实的评级等次。基于这样的原因,本文提出了不带求和过程的有界跳跃大小过程。
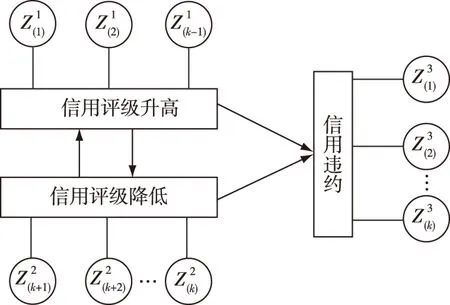
由于强度过程λl的恢复率和水平与先前信用事件的强度值成比例,且都依赖于信用事件发生时间T1,…Tn,及在每一个违约事件的自适应改变,因此,对时间Tn≤t (4) (二)随机细化过程 图1 银行间市场中信用评级变化的动态过程 (5) (6) (7) (8) (9) (10) (11) (12) (13) Wang和Yuen[16]首先把稀疏相关性理论应用于保险理赔模型中。受此启发,Liang和Wang[17]把该理论应用到信用风险模型中刻画违约相关性。本文也尝试应用稀疏相关性理论来描述银行间市场中信用事件风险传染的相关性,并给出了具有信用评级变化相关性的两个银行的联合信用安全概率。和Wang和Yuen类似,我们需要以下两个假设。 假设2 对每一个l(l=1,2,…,L),过程Nl(1) (t),Nl(2) (t),…Nl(k) (t)在给定Nl(t)的条件下是独立的。 引理1对每一个l(l=1,2,3),及k(k=1,2,…,K),Nl(t),Nl(k)(t)是前面定义的泊松过程,且0 (14) 定理1如果Ti,Tj分别是银行间市场中第i个和第j个信用事件发生的时刻(i≠j),且0 (15) 具体证明过程和文献Liang[15]相似,故省略。 银行间市场中银行主体信用评级的升高降低,甚至信用违约等信用事件是银行间市场中信用风险传染和扩散的重要源头,基于银行主体信用评级变化构建了信用风险传染建模。该模型能捕捉到银行间市场中银行主体信用质量的变化过程和不同银行间信用风险的相依性,揭示了信用事件风险在银行间市场中传染、扩散的路径和强度及信用事件风险传染的内在关系,为提升银行间市场的稳定运行、防范金融危机提供了一定的理论方法。 [1] Merton R C. On the pricing of corporate debt: The risk structure of interest rates. Journal of Finance[J]. 1974, 29: 449-470. [2] Kou, S G, Wang H. First passage times of a jump diffusion process[J].. Adv. Appl. Prob., 2003, 35: 504-531. [3] Kou S G. Petrella G, Wang H. Pricing path-dependent options with jump risk via Lap-lace transforms[J]. Kyoto economic review, 2005, 74: 1-23. [4] Fons J S. Using default rates to model the term structure of credit risk[J]. Financial analysts journal,1994,50(5):25-32. [5] Lando D. On cox processes and credit risky securities[J]. The review of derivatives research,1998, 2(2): 99-120. [6] Duffle D, Filipovic D, Schachermayer W. Affine processes and applications in finance[J]. Annals of applied probability, 2003, 13: 984-1053. [7] 王倩, T Hartmannwendels.信用违约风险传染建模[J].金融研究, 2008(10):162-173. [8] Jarrow R A, Lando. D, Yu F. Default risk and diversification: theory and empirical implica-tions[J]. Mathematical Finance, 2005, 15(1): 1-26. [9] Giesecke K, Default and information[J]. Journal of economic dynamics & control, 2006, 30:2281-2303. [10] Nakagawa H. Multi-downgrade protection with top-down approach[J]. The past, present, and future of financial technology, MTEC Journal, 2008, 15:451-481. [11] Nakagawa H. Modeling of contagious downgrades and its application to multi-downgrade protection[J]. JSIAM Letters, 2010(2):65-68. [12] Giesecke K, Baeho Kim. Risk analysis of collateralized debt obligations[J]. Operations research , 2011, 59(1):32-49. [13] S Yamanaka, M Sugihara, H Nakagawa. Modeling of contagious credit events and risk analysis of credit portfolios[J]. Asia-Pacific finan markets, 2012, 19:43-62. [14] 张晓燕,王晓婷,沈沛龙.金融包容理论下的中国银行监管研究[J].经济问题,2016(05):36-43. [15] 杜江,杨浩宇.发达国家影子银行监管对我国的启示[J]. 理论探讨,2016(3):83-87. [16] Wang G J. Yuen K C. On a correlated aggregate claims model with thinning-dependence structure, Insurance[J]. Mathematics and economics, 2005, 36:456-468. [17] Liang X, Wang G J. A Reduced model with thinning-dependence structure[J]. Chinese journal of applied probability and statistics, 2012, 28(6):655-664. [18] Ross S M. Stochastic processes[M]. New York: Wiley,1996. F832 A 1671-511X(2017)06-0074-06 2017-07-15 国家自然基金项目“基于复杂动力网络的突发事件信息同步传播行为及其模型”(71171051);河南省高校重点科研项目(18A110017)成果之一。 吴亮,河南鹤壁人,东南大学经济管理学院博士生,河南科技学院数学科学学院讲师,研究方向:信用风险分析和衍生品定价。 (责任编辑 余 敏)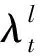
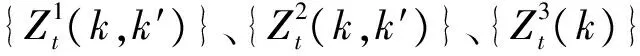

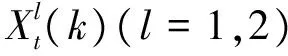


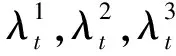
四、信用评级变化的联合概率
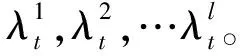
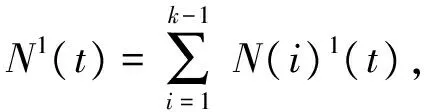

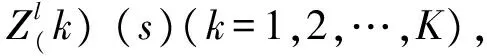

五、总 结

