经历教学:让错误生成融入新知探究
——以“多项式乘以多项式”教学为例
■魏爱凤
经历教学:让错误生成融入新知探究
——以“多项式乘以多项式”教学为例
■魏爱凤
笔者在一次课堂展示活动中,因为把学生的一些错误生成有机融入新知探究,让学生经历了较好的纠错、究错、评错的过程,受到观课教师的好评。下面是该课的一些教学片段,并附几点教学思考,供大家研讨。
一、“多项式乘多项式”的教学片段
1.教学片段1。
师:上一节课我们学习了“单项式乘多项式”,大家想想我们接下来会学习什么内容?
生1:当然是“多项式乘多项式”了。
师:对的!(师板书课题:多项式乘多项式。)你怎么知道的?
生1:我预习过,书上是这样的内容。
师:你能说说多项式乘多项式该怎么运算吗?
生1:多项式与多项式相乘,先用一个多项式里的每一项乘另一个多项式里的每一项,再把所得的积相加。
师:讲得很好,将课本上的法则背出来了,我们来看看,他对这个法则的理解究竟到达了什么程度?对于(a+b)(c+d)=ac+ad+bc+bd,你先谈谈a为什么乘到d,a和c之间有没有关系?b为什么就乘到c,b和d之间有没有关系?
生1:不是说一个多项式里每一项乘另一个多项式里的每一项吗?
师:大家觉得他的理解对不对?
生2:不对。
师:为什么?
生2:他对“每一项”的理解不正确。
师:那应该怎么理解?
生2:(上台板演)如下图的示意图,a乘到c,a乘到d,b乘到c,b乘到d。这才是符合要求的。
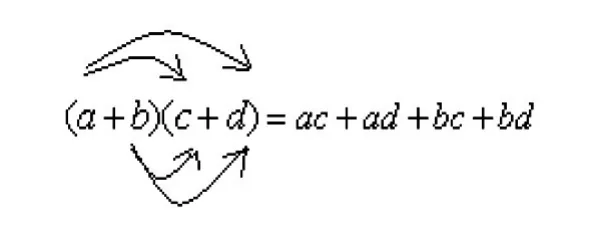
师:大家同意他这个做法吗?
众生:同意!
师:我有个问题不明白,你怎么就认为这样做是对的呢?根据什么理由来做的?谁能帮我更进一步把这个问题解决了?
学生陷入思考(看来有点困难)。
师:我提供个思路,能不能往单项式乘多项式的思路上去想呢?
生3:我们可以将a+b看作为一个整体,此时它就可以作为一个单项式来理解,它就乘到c和d。
师:这位同学想法很大胆呀,这样理解行不行?
生4:对的。
师:大家想想他这种想法有没有依据,是我们数学中的一种什么思想?
生4:整体思想。
师:对的,还有没有其他的思想方法?
生5:转化思想。
师:体现在哪里?
生:将其中一个多项式看作一个单项式,题目就转化成了单项式乘多项式了。
师:这样做下来,是几个单项式相加?
生6:四项。
师:大家思考一下,如果前一个多项式里是两项,后一个里面是三项,那算下来又是几项?
生7:六项。
师:能说说你是怎么知道是六项的吗?
生7:将前面的多项式作为单项式来看,乘到后面就有了三个单项式乘多项式,此时单项式里又有两项,然后再分别相乘,不就是六个项了吗?
师:这位同学描述得很准确,讲得也非常好。如果是两个三项的多项式相乘,那最终又是多少项呢?
生7:根据刚才的推算方法,应该是三乘三,一共九项吧。
师:很聪明,如果前面多项式是m项,后面的多项式是n项,那么乘下来是多少项?
生7:m·n项。
师:大家认为他说的这个结论怎么样?
众生:对!
师:通过我们刚才的探究,我们通过多项式乘多项式再次学习了整体思想和化归思想。原来我们的数学思想就蕴含在我们平时的学习中,而不是考试的时候才会有的哟。谁来出几个计算题来巩固所学知识?
生8:计算:(1)(3x+1)(x+2);(2)(x-8y)(x-y);(3)(x+y)(x2-xy+y2)。
师:大家来观察分析下,他所出的这3道题是不是符合我们今天所学的“多项式乘多项式”?
众生:符合!
(接下来由学生独立运算,之后再进行展示讲评。)
2.教学片段2。
展示投影,一个学生计算如下:
(3x+2y)(2x+3y)-(x-3y)(3x+4y)
=6x2+3x·3y+2x·2y+6y2-3x2+4y·x-3y·3x-12y2
=6x2+9xy+4xy+6y2-3x2+4xy-9yx-12y2
=3x2+8xy-6y2
师:大家来看看这个同学的解题过程对吗?在这个解题过程中有哪些值得我们学习的,还有哪些需要我们注意的?
生9:不对!
师:哪里不对?
生9:他没有确定符号!
师:我认为他确定了符号呀,前面的两个多项式相乘确定了符号,后面的两个多项式相乘不也是确定了符号吗?
生10:我也认为他确定了符号,但是感觉又没有确定对,这种感觉是理解了但是又好像没有理解对。
师:这位同学在学习上出现了困惑,你能说说你感觉哪里的符号没有确定吗?
生10:两个积之间的减号好像没有参与运算。
师:你的直觉很好,哪位同学能帮忙一下?
生11:我觉得这道题可分为两个多项式相乘,然后将它们的积作差。
师:分析得很有道理,他将这个计算分为两步来处理,受他的启发,我们现在要怎样来处理这个问题?
生12:将后面的多项式作为整体来看。
师:这位同学说了用整体思想来帮忙,具体用什么形式来体现呢?
生12:用中括号呀!
师:你来给大家讲讲,怎么用中括号来帮忙?
生12:(3x+2y)(2x+3y)-[(x-3y)(3x+4y)]。
师:怎么样,大家会做了吗?但是我在下面还发现一个同学的第一步是这样做的:
解:原式=(3x+2y)(2x+3y)-(x-3y)-(3x+4y)
师:大家看一看这个做法怎么样?
生13:他去掉中括号是不对的,后面两个多项式是相乘的,而不是相加减,所以不可以这样做。应该将中括号内先做乘法运算,然后再去括号。
师:分析得很到位,现在大家明白一开始解题中的错误了吗?刚才不明白的同学现在知道自己的问题出在哪里了吧。最后,我们来看一下另一个同学的正确计算吧!
展示生13的解法:
(3x+2y)(2x+3y)-(x-3y)(3x+4y)
=6x2+3x·3y+2y·2x+6y2-(3x2+4y·x-3y·3x-12y2)
=6x2+9xy+4xy+6y2-3x2-4xy+9xy+12y2
=3x2+18xy+18y2
师:这位同学做得很详细、很规范。
二、关于“经历教学”的教学思考
1.开放需要放开,促进学生经历错误。
近年来开放式教学得到不少同行的关注和推介,相对于封闭教学而言,开放式教学需要教师转变观念,在课堂上敢于放开问题、放手让学生探索、信任学生有话可说。进一步来说,教师不能害怕学生说出来的一些错误或一些不规范的语言,可以通过更加细致周到的备课来预设各种可能的情况,从而大胆放开问题,让学生参与、表达他们的思考与发现,再根据学生的回答相机引导。
上面的课例片段1中,学生对“多项式乘多项式”法则虽然有所了解,但是还不深刻,这时就因势利导,引导其他学生参与辨析其表达过程中的不规范,让一个不严谨的表达通过师生的对话趋于完善和规范;在后来的例题环节,我没有给学生出例题,而让学生自主编题,从学生提供的一组例题来看,紧扣了课时教学和训练目标,又利用了学生的错误进行化错教学,实现了较好的经历错误的教学过程。
2.对话促进生成,引导学生明辨错误。
开放式教学对教师的教学基本功,特别是课堂驾驭能力提出了较高的要求,比如在问题开放之后,学生的解答可能丰富多样,如果教师理解不到位,或者对有些学生的精彩解答视而不见,往往会错失很多生成性资源。比如一些有价值的“错误资源”,如果简单地评判为错误,轻轻滑过,则是教学机智不够;或者是教师课前对学生可能的错误、不规范的预设和研判不够充分。我们常常见到一些专家教师在课堂上不但善于捕捉学生的错误,引导学生一起参与明辨错误,而且在学生解答都很顺畅的时候,还善于“装傻”,稚化自己的思维,假装追问学生一些易错的问题,让学生参与辨明。想来,稚化思维也是促进对话生成的一种教学技艺。
经历教学是一个很大的话题,我们学校各个学科都在深入研究,特别是学科教师结合课例开展了富有成效的教学探索,笔者也是结合一次教学展示课中的纠错环节有感而发,个性化成分较多,有些认识还很肤浅,期待同行的批评指正!
(作者为江苏省海安县海陵中学教师)
[1]丁义国.“经历教学”:让学生经历知识的发生[J].初中生世界(初中教学研究),2015(2):67-69.
[2]柳伟.让学生经历数学学习的过程[J].现代教育科学:教学研究,2012(2):177-177.
[3]顾继玲.让学生经历“数学化”的过程[J].中学数学教学参考·中旬刊,2011(7):2-4.
[4]刘祖洋.让学生经历数学化的过程[J].数学教育学报,1997(3).
[5]于川.让学生经历“数学化”的数学教学策略[J].数学通报,2011,50(5):30-32.

