基于CPS-SVPWM调制的MMC-STATCOM简化算法研究

谭风雷， 杭 峰， 李义峰

(国网江苏省电力公司检修分公司，江苏 南京 211102)

基于CPS-SVPWM调制的MMC-STATCOM简化算法研究

谭风雷， 杭 峰， 李义峰

(国网江苏省电力公司检修分公司，江苏 南京 211102)

针对模块化多电平换流器(MMC)难以实现多电平SVPWM技术，提出了基于CPS-SVPWM调制的MMC控制算法。该算法是将MMC等效看作上、下2N个三相半桥的串联，合理布置两电平SVPWM生成模块的位置后，结合载波移相技术，实现多电平输出。最后，在电力系统仿真分析软件PSCAD/ EMDTC中搭建了基于模块化多电平换流器的五电平STATCOM仿真模型，结果表明基于CPS-SVPWM调制的MMC简化算法简单，控制效果好，电压利用率高，可以很好地应用到多电平MMC的控制领域，从而也验证了文中所提出的控制方法的有效性和可行性。

模块化多电平换流器； 两电平； SVPWM； 载波移相； STATCOM

0 引 言

随着数字处理器的快速发展，电力电子技术得以飞速进步。在电力电子领域，多电平技术凭借其等效开关频率高、输出电平数多、波形质量好等特点深受专家学者的青睐。H桥级联多电平换流器[1-5]具有模块化设计、拓扑结构简单、易于实现直流电容稳压等优点，在多电平领域得到广泛的应用，但其无法提供公共的直流母线，难以完成背靠背整流、直流输电工程，从而也限制了该拓扑的进一步发展。为了解决H桥级联多电平换流器存在的问题，新的拓扑结构模块化多电平换流器[6-8](MMC)应运而生，该拓扑凭借其模块化设计、冗余配置简单、均压控制简单、提供公共直流母线方便能量的双向流动等优点，已经广泛应用到多电平领域，尤其在柔性直流输电工程[9]和高压变频领域[10]有着光明的应用前景。

目前，研究模块化多电平换流器的文献[11-15]已经较多，并主要集中在拓扑结构、工作原理、数学模型、调制策略、控制方法、冗余结构以及故障分析等方面，而调制策略主要研究的是正弦脉宽调制方式(SPWM)，关于空间矢量脉宽调制方式(SVPWM)的研究甚少，文献[16]结合MMC自身的拓扑结构和工作原理，提出了一种五电平MMC的SVPWM优化算法。文献[17]提出了简化的H桥级联多电平换流器SVPWM算法，借助两电平SVPWM实现，但每个H桥对应两个独立的两电平SVPWM模块，使得算法并不简单，不易实现。文献[18] 以模块化五电平换流器为例，分析了一种适用于 MMC 的空间矢量脉宽调制(SVPWM)算法。实际上，上述文献描述的MMC空间矢量调制技术随着电平数的增加，算法会变得十分复杂，基本难以实现，无法应用到五电平以上的领域。但考虑到SVPWM开关损耗低、波形质量好、直流电压利用率高等诸多优点，特别是应用到柔性直流输电工程中，能够有效减少直流电压13.4%，从而可靠减少串联全控型功率器件的数量，在提高系统可靠性的同时极大地节约成本，因此，如果能够将多电平MMC的SVPWM算法进行简化，便于数字化实现，将是非常有意义的。

基于上述的分析，本文将单个MMC模块的上、下桥臂等效看作两个三相半桥，采用两电平SVPWM后，结合载波移相技术，提出了一种基于CPS-SVPWM调制的MMC控制算法，同时为了进一步简化SVPWM算法，结合实际的控制策略，又提出了二种基于CPS-SVPWM调制的MMC简化算法。最后，在PSCAD/ EMDTC中搭建了基于模块化多电平换流器的五电平STATCOM仿真模型，结果验证了四种控制方法的有效性和可行性。

1 两电平SVPWM在MMC中的应用

1.1 单模块MMC的SVPWM算法

图1是单模块MMC的拓扑结构。假设MMC子模块的电容电压为Vdc，则上、下桥臂都可以实现Vdc和0两种电压输出，此时单模块MMC可以输出+Vdc、0和-Vdc三种电平电压。

图1 单模块MMC拓扑结构Fig.1 Circuit configuration of single MMC

如图中虚线所示，如果将三相上桥臂的子模块电容正负极分别相互连接，构成了一个上桥臂三相半桥；同理，如果将三相下桥臂的子模块电容正负极分别相互连接，亦构成了一个下桥臂三相半桥。因此，下桥臂三相半桥与上桥臂三相半桥输出电压差值的一半即为单模块MMC的输出电压。

此时，如果上、下桥臂三相半桥均采用两电平SVPWM调制方式，即可实现单模块MMC的SVPWM技术，能够在简化SVPWM算法的同时，有效提高直流电压的利用率。

1.2 多模块MMC的SVPWM算法

图2是多单模块MMC的拓扑结构。如图中虚线所示，将上桥臂N个子模块等效看作N个三相半桥，同时将下桥臂N个子模块等效看作N个三相半桥，上、下桥臂中的每个三相半桥分别采用独立的两电平SVPWM调制模块，则共需2N个独立的两电平SVPWM模块，此时结合载波移相技术(CPS)[19-20]，即可实现多电平电压的输出。

图2 多模块MMC拓扑结构Fig.2 Circuit configuration of MMC

载波移相技术实现N+1电平输出的方式：上、下桥臂调制波的相位相差π；上、下桥臂对应子模块载波的相位相差π，相邻子模块载波的相位相差2π/N。

载波移相技术实现2N+1电平输出的方式：当N为奇数时，上、下桥臂调制波的相位相差π，上、下桥臂对应子模块载波的相位相同，相邻子模块载波的相位相差2π/N；当N为偶数时，上、下桥臂调制波的相位相差π，上、下桥臂对应子模块载波的相位相差π/N，相邻子模块载波的相位相差2π/N。

1.3 基于载波移相调制的MMC控制方法

基于载波移相的MMC的控制方法主要分为四个部分：参考电压控制、桥臂能量均衡控制、电容电压均压控制和载波移相调制。其中，参考电压控制主要用于控制期望的输出电压，包括电压外环和电流内环，电压外环用于保证直流母线侧电容总压恒定，电流内环用于跟踪参考电流；桥臂能量均衡控制主要目的是为了保证三相桥臂平分总能量，即使得各相桥臂直流总压相同；电容电压均压控制主要目的是通过重新分配桥臂中子模块的能量，使得子模块电容电压维持恒定；而载波移相调制主要是利用各个子模块的调制波采用不同调制手段，与不同移相方法的三角载波进行比较，从而产生功率器件的开关驱动信号。根据前面所述的MMC控制方法，可以得到基于CPS-SPWM调制的MMC控制算法原理框图，如图3所示。

图3 基于CPS-SPWM调制的MMC控制算法Fig.3 Control algorithm of MMC based on CPS-SPWM modulation

将图3控制原理框图中的CPS-SPWM模块替换成CPS-SVPWM模块时，即可得到基于CPS-SVPWM调制的MMC控制原理框图，如图4所示。显然，每一个MMC模块需要2个独立的两电平SVPWM模块实现，则N个MMC模块需要2N个独立的两电平SVPWM模块实现，随着N的不断增加，所需的两电平SVPWM模块也对应增加，从而使得算法复杂，难以数字化实现。

图4 基于CPS-SVPWM调制的MMC控制算法Fig.4 Control algorithm of MMC based on CPS-SVPWM modulation

根据图4可以得到基于CPS-SVPWM调制的MMC控制算法的调制波信号：

(1)

式中：Uw1pN表示上桥臂第n个模块的调制波；Uw1nN表示下桥臂第n个模块的调制波。

2 基于CPS-SVPWM调制的MMC简化算法

根据前面的分析可知：基于CPS-SVPWM调制的MMC控制算法随着模块数N的增加，所需的两电平SVPWM模块也不断增加，这样使得该算法难以应用到多模块MMC的工程领域，从而限制了该算法的使用与推广。为了克服上述问题，文中提出了两种基于CPS-SVPWM调制的MMC简化算法。

2.1 基于CPS-SVPWM调制的MMC简化算法一

简化算法一：考虑到控制环节中，上桥臂电容均压控制环之前的控制信号是相同的，同样下桥臂电容均压控制环之前的控制信号也是相同的，如果将两电平SVPWM模块移动到能量均衡控制环和电容均压控制环之间，这样就可以有效减少两电平SVPWM模块的数量，同时也能实现多电平SVPWM电压信号的输出。另外，由于两电平SVPWM模块产生的是开关时间信号，一般在零到开关周期范围内，文中为了便于分析，将其扩大到了[0,1]范围内，此时电容均压控制环需要乘以比例系数将其缩小，限幅到[-1,1]范围内后，方可加入到两电平SVPWM模块的输出信号中，生成最终的调制信号，将该信号采用载波移相技术与三角载波相比较，从而产生功率器件的开关信号，具体的控制原理如图5所示。

图5 基于CPS-SVPWM调制的MMC简化算法一Fig.5 First simplified algorithm of MMC based on CPS-SVPWM modulation

显然，针对基于CPS-SVPWM调制的MMC简化算法一而言，上、下桥臂各需一个两电平SVPWM模块，无论子模块数N是如何变化，都只需要两个两电平SVPWM模块即可实现多电平SVPWM调制技术，从而使得算法复杂度不随N变化，易于数字化实现。则基于CPS-SVPWM调制的MMC简化算法一的调制波信号可以表示成：

(2)

式中：Uw2p表示上桥臂的调制波；Uw2n表示下桥臂的调制波。

2.2 基于CPS-SVPWM调制的MMC简化算法二

简化算法二：根据简化算法一的思想，进一步简化基于CPS-SVPWM调制的MMC控制算法。考虑到能量均衡控制环之前的参考电压信号是相同的，借助简化算法一的思想，将两电平SVPWM模块继续前移到电流内环和能量均衡控制环之间，这样两电平SVPWM模块的数量进一步减少，变成了一个。同样，由于两电平SVPWM模块输出信号的范围给扩大到了[0,1]之间，此时要保证控制信号数量级一致，需要将能量均衡控制环和电容均压控制环同时乘以比例系数将其缩小，且限幅到[-1,1]范围内后，即可加入到两电平SVPWM模块的输出信号中，完成最终调制信号的生成。最后，借助载波移相技术，生成功率器件的驱动信号，具体的控制原理如图6所示。

图6 基于CPS-SVPWM调制的MMC简化算法二Fig.6 Second simplified algorithm of MMC based on CPS-SVPWM modulation

显然，针对基于CPS-SVPWM调制的MMC简化算法二而言，无论子模块数N是多少，只需要一个两电平SVPWM模块即可实现多电平SVPWM调制技术，从而使得算法得到了进一步简化，有利于数字化实现。前面基于CPS-SVPWM调制的MMC控制算法和简化算法的调制波都在[-0.5,0.5]之间，而简化算法二的调制波在[0,1]之间，为了保证三种CPS-SVPWM算法调制波的统一，需要将简化算法二的调制波减0.5，则基于CPS-SVPWM调制的MMC简化算法二的调制波信号可以表示成：

Uwave3=Uw3-0.5

(3)

式中：Uw3表示参考电压的调制波。

3 仿真分析与研究

为了验证本文所提出的基于CPS-SVPWM调制的MMC控制算法的有效性和可行性，在PSCAD/ EMDTC中搭建了基于模块化多电平换流器的五电平STATCOM仿真模型，补偿电阻为5 Ω、电感为5 mH的阻感负载，其中，电网电压有效值为380 V，子模块数量为2，子模块电容为6 mF，桥臂电抗器为2.5 mH，功率器件工作频率为5 kHz，仿真时间为1 s，步长为5 μs，同时为了绘图清晰，只绘制了控制系统稳定状态下0.9～1.0 s的波形，具体的仿真结果如图7、8、9和10所示。

图7是文中所述基于CPS-SPWM调制的MMC-STATCOM控制算法的仿真结果。显然采用SPWM方式生成的调制波为正弦波，由于SPWM调制方式的直流电压利用率为0.5，因此直流电容总压必须大于2倍的相电压峰值622 V，文中SPWM方式调制时直流母线电压目标值设定为700 V，由图7(b)可知子模块直流电容电压稳定在350V左右，最大波动为±5 V，稳压效果较好。由图7(c)可知阻感负载无功补偿后，电源电压(实际绘图中为了比较分析，电压缩小了一半)与电源电流几乎完全同相位，功率因数为1，无功补偿效果较好。由图7(d)和(e)可知三相输出电流幅值约为20 A，波形高度正弦化，谐波畸变率THD低，为3.4%，而补偿后，三相电源电流完全对称，基本只含有无功功率，从而表明基于CPS-SPWM调制的MMC-STATCOM控制算法的控制效果好，稳压效果佳。

图7 基于CPS-SPWM调制的MMC-STATCOM控制算法的仿真结果Fig.7 Simulative results of control algorithm of MMC based on CPS-SPWM modulation

图8、9、10分别三种是基于CPS-SVPWM调制的MMC-STATCOM控制算法的仿真结果。显然采用SVPWM方式生成的调制波为马鞍波，由于SVPWM调制方式的直流电压利用率为0.577 4，因此直流电容总压必须大于539 V，文中将SVPWM方式调制时直流母线电压目标值设定为600 V。

图8 基于CPS-SVPWM调制的MMC-STATCOM控制算法的仿真结果Fig.8 Simulative results of control algorithm of MMC based on CPS-SVPWM modulation

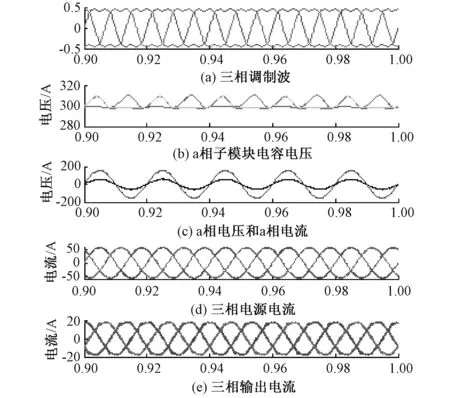
图9 基于CPS-SVPWM调制的MMC-STATCOM简化算法一的仿真结果Fig.9 Simulative results of the first simplified algorithm of MMC based on CPS-SVPWM modulation

图10 基于CPS-SVPWM调制的MMC-STATCOM简化算法二的仿真结果Fig.10 Simulative results of the second simplified algorithm of MMC based on CPS-SVPWM modulation

由图8(b)、9(b)、10(b)可知，基于CPS- SVPWM调制的MMC-STATCOM控制算法的子模块电容电压稳定在300 V左右，三种CPS- SVPWM调制算法的最大电压波动分别为10 V、10 V和4 V，表明基于CPS-SVPWM调制的MMC- STATCOM简化算法二的稳压效果最好，甚至要好于基于CPS-SPWM调制的MMC-STATCOM控制算法。由图8(c)、9(c)、10(c)可知无功补偿后，三种CPS-SVPWM调制算法控制效果较好，无功基本全部被补偿，功率因数几乎达到了1。由图8(d)和(e)、9(d)和(e)、10(d)和(e)可知三相电源电流和输出电流高度对称，正弦化程度高，畸变率低，其中三相输出电流THD分别为4.4%、4.8%和2.7%，表明于CPS-SVPWM调制的MMC-STATCOM简化算法二的控制效果最好。

综上所述，为了便于分析和比较，绘制了4种MMC-STATCOM控制算法的优缺点表，如表1所示。分析该表可知：在相同运行环境下，仿真总时间长度为1 s时，软件的实际运行时间最短的是CPS- SPWM；三相输出电流畸变率THD以及电容直流电压波动最小的是CPS-SVPWM3，表明基于CPS-SPWM调制的MMC-STATCOM控制算法相对最为简单，易于实现，而基于CPS-SVPWM调制的MMC-STATCOM简化算法二谐波畸变率低，电容电压波动小，控制效果相对最好，同时考虑到SVPWM调制方式的电压利用率要高于SPWM，因此，基于CPS-SVPWM调制的MMC-STATCOM简化算法二整体控制效果最好，能够在MMC领域得到较好的运用。

表14种MMC-STATCOM控制算法的特点

Tab.1 Characteristics of four control algorithm of MMC-STATCOM

算法类型运行时间/sTHD/(%)电容电压波动/V直流总压/VCPS-SPWM1053.45700CPS-SVPWM13124.410600CPS-SVPWM21764.810600CPS-SVPWM31262.74600

4 结 论

(1)将单个MMC模块的上、下桥臂分别看作两个三相半桥，采用两电平SVPWM，结合载波移相技术，提出了三种基于CPS-SVPWM调制的MMC控制算法。

(2)在PSCAD/ EMDTC中搭建了基于模块化多电平换流器的五电平STATCOM仿真模型，结果表明基于CPS-SVPWM调制的MMC-STATCOM简化算法二算法简单，控制效果好，电压利用率高，可以很好的应用到MMC控制领域，从而也验证了文中所提出的控制方法的有效性和可行性。

[1] 窦真兰, 程孟增, 李素英, 等. 三电平 NPC 整流器控制及中点电位平衡控制技术[J]. 电力自动化设备, 2011, 31(10): 32-37.

[2] 李宁, 王跃, 雷万钧, 等. 三电平 NPC 变流器 SVPWM 策略与SPWM策略的等效关系研究[J]. 电网技术, 2014, 38(5): 1283-1290.

[3] 李卫超, 马伟明, 汪光森, 等. 中点钳位型H桥级联单相逆变器新型空间矢量脉宽调制方法[J]. 中国电机工程学报, 2014, 34(30): 5313-5319.

[4] 徐榕, 于泳,杨荣峰, 等. H 桥级联 STATCOM 直流侧电压平衡控制方法[J]. 电力自动化设备, 2015, 35 (5): 15-22.

[5] 徐榕, 于泳,杨荣峰, 等. 基于无源性理论的H 桥级联STATCOM 非线性控制策略[J]. 电力自动化设备, 2015, 35 (1): 50-57.

[6] 汤广福, 罗湘, 魏晓光. 多端直流输电与直流电网技术[J]. 中国电机工程学报, 2013, 33(10): 8-17.

[7] 李金科, 金新民, 吴学智, 等. 模块化多电平变流器模块电压纹波抑制策略及应用[J]. 中国电机工程学报, 2016, 36(7): 1892-1899.

[8] 张建坡, 田新成, 尹秀艳. 模块化多电平换流器直流输电控制策略[J]. 电力自动化设备， 2015, 35(11): 103-108.

[9] 吴浩, 徐重力, 张杰峰, 等. 舟山多端柔性直流输电技术及应用[J]. 智能电网， 2013，1(2):22-26.

[10] 商姣. 基于模块化的的高压变频装置研究[D]. 南京: 东南大学, 2013.

[11] 李探, 赵成勇, 李路遥, 等. MMC-HVDC子模块故障诊断与就地保护策略[J]. 中国电机工程学报, 2014, 34(10): 1641-1649.

[12] 王宝安, 谭风雷, 商姣. 模块化多电平换流器模块冗余优化配置方法[J]. 电力自动化设备, 2015, 35(1): 13-19.

[13] 王姗姗, 周孝信, 汤广福, 等. 模块化多电平电压源换流器的数学模型[J]. 中国电机工程学报,2011,31(24): 1-8.

[14] 李强, 贺之渊, 汤广福, 等. 新型模块化多电平换流器空间矢量脉宽调制方法[J]. 电力自动化设备, 2010, 34 (22): 75-79.

[15] 李强, 贺之渊, 汤广福, 等. 新型模块化多电平换流器 空间矢量脉宽调制的通用算法[J]. 电网技术, 2011, 35 (5): 59-64.

[16] 康文. 基于空间矢量脉宽调制的新型模块化多电平整流器研究[D]. 长沙: 湖南大学, 2013.

[17] 王宝安, 白晨阳, 陈豪, 等. 基于CPS-SVPWM调制的链式STATCOM直流侧电压控制策略[J]. 高压电器, 2015, 51(12): 165-173.

[18] 康文. 基于空间矢量脉宽调制的新型模块化多电平整流器研究[D]. 长沙: 湖南大学, 2013.

[19] 谭风雷. 基于MMC的电机拖动系统控制策略研究[D].南京: 东南大学, 2015.

[20] 李宁, 王跃, 蒋应伟, 等. 三电平 NPC 变流器虚拟空间矢量调制策略与载波调制策略的内在关系研究[J]. 电网技术, 2014, 38(1): 166-174.

Research of MMC-STATCOM Simplified Algorithm Based on CPS-SVPWM Modulation

TAN Fenglei, HANG Feng, LI Yifeng

(State Grid Jiangsu Electric Power Maintenance Branch Company, Nanjing 211102, China)

New MMC control algorithm based on CPS-SVPWM modulation is proposed to solve the problem that MMC is difficult to realize multi-level SVPWM technology. Regarding MMC as 2N three-phase half bridges of upper and lower arms, the MMC control algorithm based on CPS-SVPWM modulation rearranges the position of the two-level SVPWM generation module reasonably and combines with carrier phase shifting technology to achieve multi-level output. Finally, simulative model of five-level STATCOM based on MMC is established in the PSCAD/EMDTC and the results show that the MMC simplified algorithm based on CPS-SVPWM modulation can be applied to the control field of MMC, with simple algorithm, good performance and high voltage utilization, which verifies validity and feasibility of the control method provided in this paper.

modular multilevel converters; two-level; SVPWM; carrier phase shifting; STATCOM

2017-03-26.

10.3969/j.ISSN.1007-2691.2017.06.08

TM46

A

1007-2691(2017)06-0047-07

谭风雷(1989-)，男，从事特高压电网变电运维的工作；杭峰(1978-)，男，工程师，从事特高压电网变电运维的工作；李义峰(1983-)，男，工程师，从事特高压电网变电运维的工作。