改进的k中心点算法在茶叶拼配中的应用

邢光林，胡一然，孙 翀，帖 军

(中南民族大学 计算机科学学院，武汉 430074)

改进的k中心点算法在茶叶拼配中的应用

邢光林，胡一然，孙 翀，帖 军

(中南民族大学 计算机科学学院，武汉 430074)

为了提高茶叶拼配效率，节约人工成本，实现茶叶企业效益最大化，探讨了将茶叶拼配问题建模成多维层次空间聚类问题，并通过定义多维概念分层空间中的相似性度量准则，提出了改进的k中心点算法求解最优拼配方案，并引入Dewey编码提高了求解效率.根据真实数据集上的实验表明：同等实验条件下较人工拼配方式而言，文中所提出的茶叶拼配智能化求解方法大大提高了茶叶企业工作效率和经济利益.

茶叶拼配；空间聚类；多维概念分层；Dewey编码；k中心点算法

我国是最早种植茶树、最早进行茶叶加工的国家，消费者对茶饮料的喜爱更是推动了茶叶市场的发展.在快速发展的茶叶市场中，茶叶拼配技术作为茶叶加工的一种工艺，多为商品茶加工企业采用，尤其是在我国非产茶区的北方茶叶加工企业，一般只能对茶叶进行拼配加工.茶叶拼配是指将两种以上形质不一，具有一定共性的茶叶，拼合在一起的作业，是一种常用的提高和稳定茶叶品质、扩大货源、增加数量、获取较高经济效益的方法[1].

传统的茶叶拼配主要是依赖茶叶专家的经验，其拼配方式通常也取决于茶叶的品质及数量.国内已有众多学者对茶叶拼配问题进行了深入研究，大部分研究在于高效机器的应用[2,3]和拼配技术的提高[4,5]等方面.这种传统的人工拼配方式对于拼配人员的技术要求过高，同时由于茶叶加工企业众多，不同企业因其茶叶质量和数量的不同，对拼配而成的成品茶品质要求也不同.这将导致拼配专家在茶叶拼配过程中需要花费大量时间和精力为不同的企业制定不同的拼配方案，更难以比较各种方案的成本并加以优化，即使是对于同一企业，在茶叶品质和库存变化的情况下，也需要调整拼配方案.

近年来，随着计算机技术的高速发展，传统行业人工操作越来越多地被智能化系统所替代，在茶叶拼配中应用计算机技术将大幅提高工作效率[6]，降低企业成本.本文提出将改进的k中心点算法应用到茶叶拼配技术中，首先将茶叶拼配问题抽象为数据表的语义汇总问题，再建模成空间聚类问题，利用空间聚类汇总算法将相似的茶叶合并.传统的空间聚类算法只适合欧氏距离度，而茶叶拼配问题属性维度多为概念分层类型，因此本文提出了多维概念分层空间中的相似性度量准则，从而改进了k中心点算法.在数据预处理过程中，通过Dewey编码快速将原始数据映射到多维层次空间的点集.本文提出的方法不仅为茶叶企业提供了一个通用的、低成本、高效率的茶叶拼配方案，同时也为企业的成本优化决策提供了重要帮助.

1 问题描述

本节首先将茶叶拼配问题模型化为数据表的语义汇总问题，再对表语义压缩进行约定和形式化，最后将茶叶拼配问题转化为空间聚类问题，并提出多维概念分层空间中的距离度量.将茶叶拼配这一实际生产中的问题建模为聚类问题，能更好地利用数据挖掘的思想和技术对该问题进行高效求解.

1.1 茶叶拼配问题模型化

茶叶拼配问题的核心是合并形质不一、具有一定共性的茶叶，本文将形质不一、具有一定共性定义为“相似”，因此茶叶拼配工作可描述为合并相似的茶叶.对茶叶相似性的判断实际是对茶叶品种、加工工艺等多方面信息的综合考量.本文以茶叶的名称、茶树品种、加工工艺和产地这4方面的信息为例，将拼配前的原茶叶信息以数据表的形式表示，如表1所示，其中附加列ID用于唯一标识元组.

表1 茶叶信息Tab.1 Tea information

在表1中，每一种待拼配的茶叶用一个元组表示，拼配所需考量的信息用数据表中的属性值表示，因此茶叶拼配问题可描述为数据表的缩减问题，即考虑语义因素的汇总数据表，使用少量“抽象”元组来表示大量“详细”元组.

1.2 符号约定和形式化定义

本文的表汇总技术利用表中各个属性的属性值概念分层[7]对原始茶叶信息数据表进行元组泛化.属性值概念分层是一种树形层次结构，描述了属性值域上的分类关系，文献[7]对建立该结构的方法有说明，在此不做详述.表1中的茶树品种、加工工艺和产地三个属性的概念分层如图1所示，以分类型的属性加工工艺为例，其属性值可以从“加工工艺小类”泛化到层次较高的“加工工艺大类”.在概念分层结构中，节点的位置决定了语义的“详细”程度和属性值的泛化能力：位置越接近根节点的语义信息越少，而其泛化的范围越大，任意节点能泛化以其为根的子树内的所有节点.

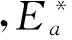
根据上述约定，下面给出属性值泛化及元组泛化等相关形式化定义.

定义1(属性值语义量)对于属性a中的任意属性值x，其语义量为x在概念分层中对应节点的层数，用ASemantic表示，即x.ASemantic=level(x).

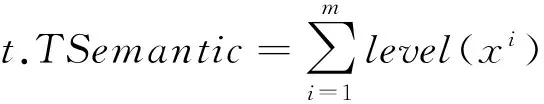
定义4(元组间泛化关系)若对于任意两个元组t1和t2，其第i个属性值均有t1[i] ∠t2[i]成立，则称t1可以泛化t2，用t1∠t2表示.

定义5(最优泛化)给定属性a的任意属性值集Sa和属性值x，若满足：(1)Sa中的任意属性值对应的节点均为ha中以label(x)为根节点的子树上的叶节点；(2)不存在当Sa中的任意属性值对应的节点均为ha中以label(x′)为根节点的子树上的叶节点时，label(x′)子树上的节点数大于label(x)子树上的节点数，则称x为Sa的最优泛化属性值，表示为x∠optSa.若泛化元组tc的每个属性值均是元组Ts中所有元组对应属性值集的最优泛化属性值，则称tc是Ts的最优泛化元组，表示为tc∠optTs.

定义6(语义损失)对于属性a中任意两个属性值x1和x2，若存在关系x2∠x1，则其语义损失为x2与x1的语义量之差，用AInfoLoss(x2,x1)表示，即AInfoLoss(x2,x1) =x2.ASemantic-x1.ASemantic.对于任意两个元组t1和t2，若存在关系t2∠t1，则其语义损失为t2与t1的语义量之差，用TInfoLoss(t2,t1)表示，即TInfoLoss(t2,t1) =t2.TSemantic-t1.ASemantic.

1.3 茶叶拼配转换为空间聚类问题

根据1.2节中关于表语义汇总的相关约定和定义，本文给出1.1中模型化后的茶叶拼配问题的形式化定义: 给定原始茶叶信息表T和泛化元组后的元组个数k，构建满足如下条件的汇总表T′：(1)T′中的任意元组可以泛化T中的「|T|/k⎤个元组；(2)泛化后的元组语义损失之和最小.

泛化过程中，Tx表示元组集的泛化元组集合，tx为Tx中具有最大语义量的泛化元组，则tx为元组集的最优泛化元组.所以当原始表T中的分组确定后，用每个分组的最优泛化元组来替换分组中的原始元组即可使T′语义量最大.由此可见，T′的质量取决于T中的分组.本文将线性空间中表的元组表示为空间中的点，则表中元组的分组问题可被表示为多维空间中点的聚类问题.

在此本文可将茶叶拼配问题描述为：在多维空间中，将点集T聚类成k个子簇，每个子簇用一个点表示，并且使得语义损失最小，定义如下：

定义7(空间距离)对于T中的任意两点t1和t2，称其最优泛化元组的语义量为两点间的空间距离，用d(t1,t2)表示，即d(t1,t2) =t.TSemantic，其中t∠opt{t1,t2}.

2 基于k中心点聚类的茶叶拼配算法

针对茶叶拼配空间聚类问题，本节首先引入Dewey编码，在原始数据中利用该编码表示概念分层树中的泛化关系，提高语义量的计算效率；随后提出基于改进的k中心点算法高效地对空间中的原始数据点进行聚类.

2.1 Dewey编码

Dewey编码(点分十进制编码)是一种快速树编码，已有超过一百年的历史，常用于树的索引及检索.其基本思想是前缀编码.本文根节点编码设置为“0”，若节点t的编码为“0……xx”，则其第i个子节点的编码表示为“0……xxi”.如图1所示，每个节点的Dewey编码为其概念分层树中每个节点右下角的数字.通过Dewey编码标识节点可快速判断概念分层树中节点的分层关系和节点间的泛化关系，使用节点的Dewey编码能快速计算点间的空间距离.Dewey编码方案具有编码效率高、解码速度快的优点，被广泛应用于树形结构编解码.

以表1中的茶叶信息属性值为例，本文在聚类过程中只考虑茶树品种、加工工艺和产地这三方面信息，其Dewey编码如表2所示.使用Dewey编码后的属性值语义量等于其编码长度，元组语义量等于其属性值语义量的累加和，如表2中t1.TSemantic= |011| +|012| + |0112| = 10.

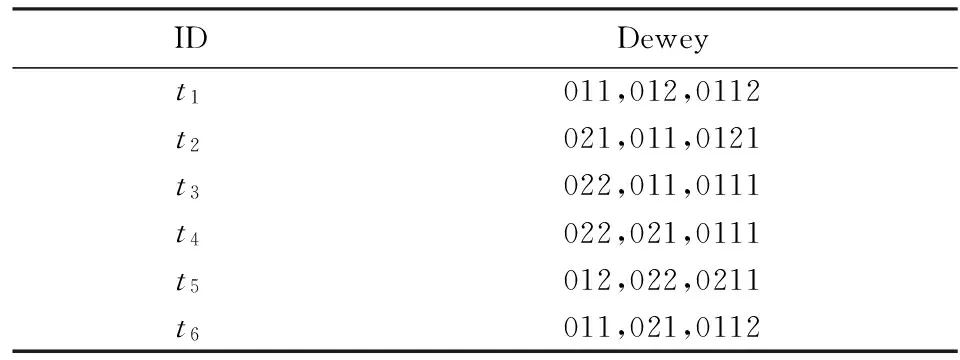
表2 茶叶信息属性值Dewey编码Tab.2 The Dewey coding of tea information attribute value

给定元组集的Dewey编码集，将该编码集在各维属性上做投影操作，所得字符串集的最长公共前缀是该元组集上最优泛化元组的Dewey编码.以表2中t2和t3为例，其最优泛化元组用t23表示，则t23各属性的Dewey编码为{02,011,01}，在多维空间中，t2和t3间的空间距离为d(t2,t3) =t23.TSemantic= |Dewey(t23)| = 2+3+2 = 7.

2.2 基于k中心点的空间聚类算法

茶叶拼配空间问题的关键在于聚类过程中的元组划分，k中心点算法[8,9]是一个常用的聚类算法，其划分是基于最小化所有对象与其对应的参照点之间的相异度之和的原则来执行的.本文采用k中心点的思想来求解茶叶拼配空间聚类问题.

k中心点聚类算法的基本思想可描述为：首先任意选择原始点集中的k个对象为中心点，计算剩余对象与这k个点之间的距离，并将其分配到与其最近的中心点；然后通过多次迭代，反复用非中心点代替中心点并计算替换代价的方法，使聚类质量达到最优.

根据上述思想以及本文所提出的多维概念分层空间中的距离度量，本文设计茶叶拼配求解算法如算法1.

算法1 TBBOK(T,K,Num)

Input:T, 原始数据元组；

K，输出子簇的个数

Num: 最大迭代次数

Output:T′,拼配后数据元组

Begin

Initial(T);

N←0;

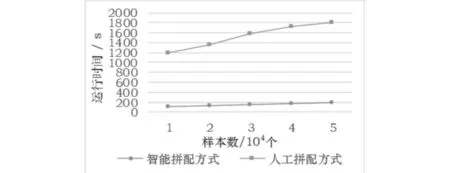
While (N

DT←InitDivision(T);

RPoint←RSelect(T);

S←ReplaceCost(RPoint,DT);

If (S<0)

Replace(RPoint,DT);

else

T′←DealWithOB(DT);

Break;

End If

N←N+ 1;

End While

End

算法中Initial(T)对聚类输入进行初始化，完成对原始数据元组的编码工作；N记录了当前迭代次数.DT为三元组(GCP,GCPCode,GPSet)的集合，GCP和GCPCode分别记录了分簇中心点的ID和Dewey编码，GPSet记录分簇包含的点集，InitDivision函数完成对原始数据编码集的初始化工作，即随机选取k个点作为初始的中心点，指派每个剩余对象给离它最近的中心点所在的分簇.RSelect函数在原始数据点中随机选择一个非中心点对象.ReplaceCost计算选中的非中心点替换DT中某一中心点的代价，如果替换代价为负，使用RePlace函数完成替换工作，并形成新的簇.当k个中心点不再发生变化，或者迭代次数达到用户设置的最大值时，算法结束.

假设算法输入规模为n，输出规模为b，则算法需要循环(n-b)次.每次循环至少遍历一次数据，至多遍历次数为数据的常数倍，因此每轮循环中的算法处理时间可以认为是O(n).故算法的执行代价在最差情况下为O(n2).

3 实验与分析

3.1 实验环境

本文实验的数据集采用真实数据集Tea Set，该数据集含有约50000条元组，选择数据集中的3个属性作为实验对象，其属性的相关信息描述见表3.实验采用的硬件：主频为1.6GHz的CPU以及1GRAM(DDR)；TBBOK算法使用CSharp语言,在VS.NET2005环境下实现.

表3 Tea Set数据集描述

下文主要从算法执行时间分析实验算法.

3.2 实验结果与分析

本文在不同样本数(原始数据的元组数)的情况下对TBBOK算法的执行效率和人工拼配方式进行考察.实验目的是比较拼配数据智能处理与人工处理方式效率的差异以及样本数的变化对算法效率的影响.实验结果如图2所示.

根据图2所示结果，对于104数量级的数据，使用拼配数据智能处理求解拼配方案时间上远低于人工拼配.此外，随着样本数的增加，两种拼配方式求解拼配方案的时间均呈线性增加，但总体来说，样本数对算法运行效率的影响较小.因此，将茶叶拼配问题作为空间聚类问题进行智能化求解可大幅提高拼配效率，减少工作时间，节约企业成本.

图2 人工拼配方式和智能拼配方式比较Fig.2 Comparison of artificial blending way and intelligent blending way

4 结束语

本文通过Dewey编码将茶叶拼配问题中原始信息元组编码成层次空间中的点，同时将茶叶拼配问题转化为空间聚类问题，再结合k中心点算法的思想求解该问题.通过将茶叶拼配工作利用智能化数据处理方法进行求解，无论是在茶叶企业实际生产中运用，还是作为企业决策支持系统的一个重要组成部分，均比传统的人工方法更高效、更精确，同时也为茶叶企业提供了一个通用的、低成本的茶叶拼配方案，具有社会和经济效益.

下一步的工作可考虑对该问题中原始数据的各属性计入权重，使拼配工作更能满足不同用户的精

确需求；同时，对已有茶叶拼配方案进行学习和挖掘，利用半监督学习求解茶叶拼配问题将是今后的研究重点.

[1] 青青柳岸. 茶叶的拼配技术工艺[EB/OL].( 2011-09-04). [2011-12-23]. http://blog.sina.com.cn/s/blog_442cf7e50100tf4j.html.

[2] 王国海. 滚筒匀堆机在茶叶拼配中的实践[J]. 广东茶叶, 2003(1): 31-32.

[3] 肖宏儒，朱志祥. 茶叶机械化加工装备技术发展趋势[J]. 农业装备技术, 2005, 31(6): 7-10.

[4] 施和森. 出口绿茶的拼配技术与品质管理[J]. 中国茶叶, 1999 (5): 10-11.

[5] 童华荣，龚正礼. 茶叶拼配的混料设计研究[J]. 茶叶科学, 2004, 24(3): 207-211.

[6] 琚春华，王光明. 一个基于知识的规划型出口茶叶拼配决策支持系统PTBDSS的研究与实现[J]. 计算机研究与发展, 1998, 35(2): 145-149.

[7] 金胜男. 基于多层关联规则的概念分层知识库中知识发现的研究[D]. 天津:天津大学, 2006.

[8] Han Jiawei, Kamber M. 数据挖掘概念与技术[M]. 范 明，孟小峰，译. 北京：机械工业出版社, 2001.

[9] 刘金岭. k中心点聚类算法在层次数据的应用[J]. 计算机工程与设计，2008, 29(24): 6418-6422.

ApplicationoftheImprovedk-MedoidsAlgorithminTeaBlending

XingGuanglin,HuYiran,SunChong,TieJun

(College of Computer Science, South-Central University for Nationalities, Wuhan 430074, China)

In order to improve the efficiency of tea blending, saving the labor costs and achieving the maximum profit for tea enterprise, we model the problem of tea blending as the spatial clustering based on multi-dimensional hierarchy. We define the similarity measure criteria in multi-dimensional conceptual hierarchy space to improve k-medoids algorithm and solve the optimal blending scheme. By introducing Dewey coding, we improve the solving efficiency. The experiment on real life dataset shows that, compared with the manual way under the same experimental conditions, the intelligent tea blending scheme proposed in this paper has greatly improved the working efficiency and economic benefits for tea enterprises.

tea blending; spatial clustering; multi-dimensional conceptual hierarchy; Dewey coding; k-medoids algorithm

2017-05-05

邢光林(1972-)，男，副教授，博士，研究方向：移动计算与分布式系统，信息安全，E-mail: xingguanglin@gmail.com

国家科技支撑计划项目子课题(2015BAD29B01)；中央高校基本科研业务费专项资金资助项目(CZP17007)

TP391

A

1672-4321(2017)04-0126-05