准分布式FBG对应变和温度双参数分离测量的实现

李 薇， 侯 睿，张志俊

(中南民族大学 计算机科学学院，武汉430074)

准分布式FBG对应变和温度双参数分离测量的实现

李 薇， 侯 睿，张志俊

(中南民族大学 计算机科学学院，武汉430074)

为解决光纤Bragg光栅(FBG)的应变与温度交叉敏感问题，提出了一种将两个参数相同的FBG分别放置于承重梁上下两端面同时感知应变与温度的方法，通过理论分析计算，实现了应变、温度双参数传感的目的. 该方法既克服了传统双参数分离方法的各种限制，又简化了分离算法. 标定与测量实验结果表明：在温度0-100℃、应变0-40MPa范围内，FBG的应变与温度响应曲线呈现良好的对应关系，最大相对误差分别为3.7%和4.2%. 应变与温度分离测量方案简单易行，将其应用于准分布式应变定位领域，可以实现应变位置的识别与预警，具有较高的实际应用价值.

准分布式；光纤布拉格光栅；双参数测量

光纤Bragg光栅(FBG)是一种用紫外激光直接写入法在单模光纤上刻有沿光纤轴向折射率变化光栅的新型光纤器件，具有体积小、重量轻、抗电磁干扰和耐腐蚀性等优点[1]. 与此同时，FBG便于与光纤结合，使得全光纤化的一维光子集成成为可能[2]，因此被广泛应用于航空航天、智能楼宇等传感监测领域[3，4]. FBG通过Bragg中心波长的偏移来感知被测量，在实际测量中，一直存在应变和温度的交叉敏感问题[5]. 现有的应变和温度双参数分离测量方法主要有以下几种：1)双波长矩阵法[6]，该方法通过引入新的参数，来有效解决应变和温度的交叉敏感问题，但其对所采用光栅传感器的应变灵敏度和温度灵敏度有一定限制条件；2)两段式FBG结构法[7]，基于FBG纤芯有效折射率与纤芯半径的良好相关性，实现双参数测量，但此方法需要用HF酸腐蚀部分FBG传感器区域，制作难度较大；3)LPG/FBG混合法[8]，利用LPG和FBG对应变和温度敏感性的差异，实现应变和温度的同时测量，该方法需引入反射强度参量，且对反射端和透射端采集数据的同时性要求较高，使得测量系统操作较为复杂.为了解决该交叉敏感问题，本文采用分别放置于承重梁上下两端面的光栅对来同时感知应变和温度变化，以实现应变、温度双参数传感的目的. 此外，本文围绕准分布式的FBG应变定位原理进行了探讨，并进行了较详尽的实验标定与测量.

1 双参数测量光栅对结构模型与理论分析

双参数测量光栅对结构模型如图1所示，两个相同的光纤Bragg光栅FBG1和FBG2分别粘贴在承重梁的上下两端面，宽带光源发出的光经过隔离器与耦合器进入到光栅中，采用光谱仪观测反射后的中心波长变化. 两个光纤Bragg光栅的初始中心均为λB，如图2所示，当压力传送产生作用时，承重梁的形变使得位于上端面的FBG1被压缩，位于下端面的FBG2被拉伸，且两个光纤光栅所受的应变始终大小相等，但方向相反. 此时，两个光纤Bragg光栅的中心波长分别变为λB1和λB2，均发生了偏移.

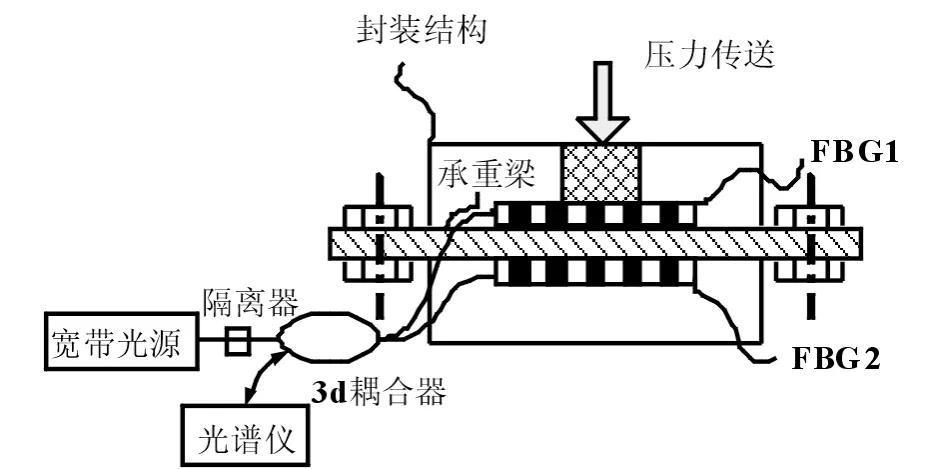
图1 光栅对结构模型Fig.1 Structure model of grating pairs

光纤Bragg光栅的中心波长偏移与应变和温度有如下关系[9]：

ΔλB=Kεε+KTΔT,

(1)

由式(1)可知，FBG中心波长偏移量ΔλB与光栅的灵敏度系数Kε、应变量ε、光栅温度系数KT和温度变化量ΔT有关，可将其等效为：

ΔλB=Δλε+ΔλT,

(2)

其中，Δλε为仅由应变引起的中心波长偏移，ΔλT为仅由温度变化引起的中心波长偏移. 当承重梁发生形变时，光栅对FBG1和FBG2的反射光中心波长均会产生偏移，如图2所示，FBG1的中心波长偏移至λB1，FBG2的中心波长偏移至λB2.

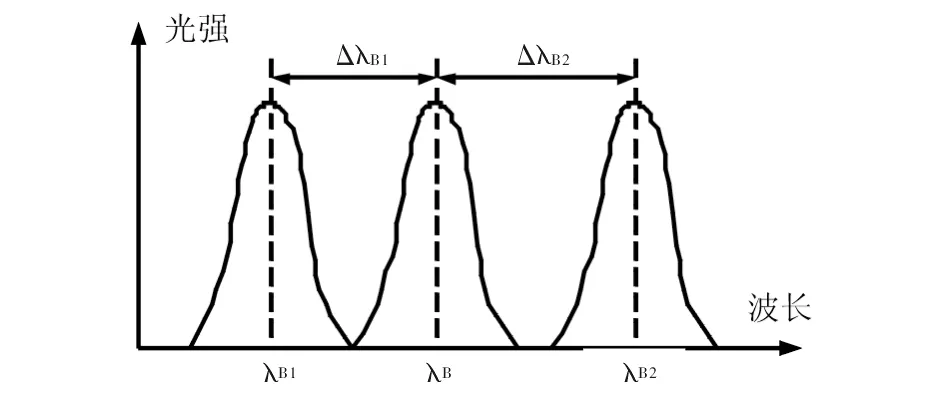
图2 光栅对反射光谱Fig.2 Reflectance spectra of grating pairs

FBG1和FBG2的中心波长偏移量分别为ΔλB1和ΔλB2，对应有：

ΔλB1=λB1-λB=Δλε1+ΔλT1,

(3)

ΔλB2=λB2-λB=Δλε2+ΔλT2.

(4)

两个光纤Bragg光栅采用同一光敏光纤写制而成，故其温度特性可视为相同，温度的变化不会引起反射光谱峰值间隔的变化[10]，即：

ΔλT1=ΔλT2.

(5)

当承重梁弯曲时，仅考虑应变引起的中心波长变化，若FBG1的Bragg波长减小了Δλε1，则FBG2的Bragg波长则相应增大了Δλε1[11]，即：

Δλε1=-Δλε2.

(6)

由式(3)～(6)可得：

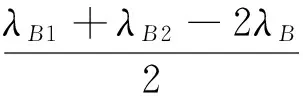
(7)

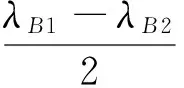
(8)

由式(7)、(8)可知，根据光谱仪观测到的波长偏移状态，可分别识别出应变量和温度值. 既能够克服双波长矩阵法中对光栅传感器的应变灵敏度和温度灵敏度的限制条件，又无需进行两段式FBG结构法中的特殊光栅写制和LPG/FBG混合法中的多参量测定，仅根据中心波长的偏移状态即可解决测量过程中应变和温度的交叉敏感问题.

2 准分布式多光栅对应变定位原理

将上述双参数测量光纤Bragg光栅等间距布置于承重梁上，如图3所示，并对光栅对进行编号(1#, 2#，…，n#). 当重物置于某光栅对上时，承重梁将产生形变，从而使得承重梁上的光栅对均随其发生形变. 各光栅对的反射光经过MOI-SM125波长解调仪，由PC上位机中的LabVIEW软件解调出峰值波长值. 由式(7)、(8)可知，当重物作用在某光栅对上时，该光栅对中的两个光栅中心波长的相对偏移量最大，从而能够识别出被施加重物的光栅对编号.

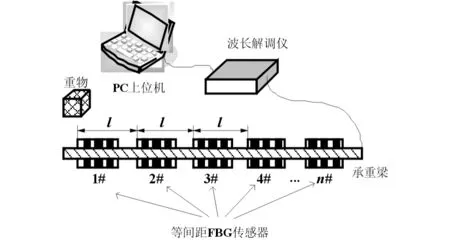
图3 基于多光栅对准分布式应变点定位原理图Fig.3 Schematic diagram of stain point location based on quasi-distributed grating pairs

3 实验与结果分析

将图1所示的带有封装结构的光纤Bragg光栅测试模块放入高低温箱中，模拟承重梁受力状态，进

行温度和应变的双参数标定实验研究. 实验所采用光栅的Bragg波长均为1558.6nm，宽带光源发出的光经过3dB耦合器进入FBG1和FBG2中，反射光进入光谱仪以便观测光谱状态.

首先进行应变标定实验. 保持高低温箱的温度恒定为20℃，以0MPa压强作为加载起点，按照每次2MPa的压强间隔不断加载，直至压强为40MPa；然后以40MPa作为起点，按照2MPa的压强间隔做卸载，直至压强为0 MPa，并记录光栅对的中心波长变化情况，反复5次加载与卸载，剔除一些明显误差数据，可拟合出实验所用光纤Bragg光栅的应变响应曲线，如图4(a)所示. 光纤Bragg光栅的温度标定实验则保持应变恒定不变，在0～100℃范围内，以5℃为间隔量调节高低温箱的温度，测量每个稳定状态下的光栅中心波长值，从而拟合出光纤Bragg光栅的温度响应特性曲线，如图4(b)所示.

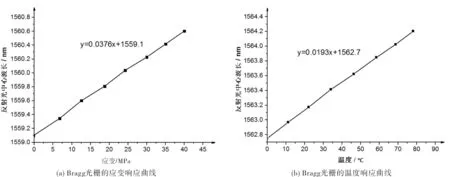
图4 Bragg光栅的测量响应曲线Fig.4 Measurement response curve of Bragg grating

根据上述实验所得标定曲线可得光栅的灵敏度系数与温度系数，结合前面所述理论分析部分的式(7)、(8)，能够通过测量系统上位机测算出实时的应变与温度测量值，并与实际值进行比较，如图5所示. 光纤Bragg光栅实际值与测量值之间偏差较小，应变测量的最大相对误差发生在20MPa附近，约为3.7%，温度测量的最大相对误差发生在45℃附近，约为4.2%.

在上述实验条件下，进行了准分布式单点应变定位实验. 承重梁上下两端面分别贴有两根传感光纤，每条传感光纤上制了6个Bragg光栅，呈等间隔均匀排列，并对其进行编号，如图3所示. 将重物分时放置于各段光栅对上，采用上述实验结果测算出每个应变状态下，各段光栅对中心波长峰值偏移量的最大值，如图6所示. 当重物施加于某编号的光栅对上时，此光栅对的中心波长峰值偏移最明显. 由此可见，通过峰值偏移程度可推算出应变产生的光栅对编号.

4 结论

本文通过分析准分布式FBG应变定位原理，采用分别放置于承重梁上下两端面的光栅对来同时感知应变和温度变化，通过较详尽的实验标定与测量可得到如下结论.

(1)采用两个相同的光纤Bragg光栅，分别粘贴于承重梁的上下端面，实现承重梁发生形变时，两个Bragg光栅的中心波长朝不同方向偏移，仅根据中心波长的偏移状态即可解决测量过程中应变和温度的交叉敏感问题.

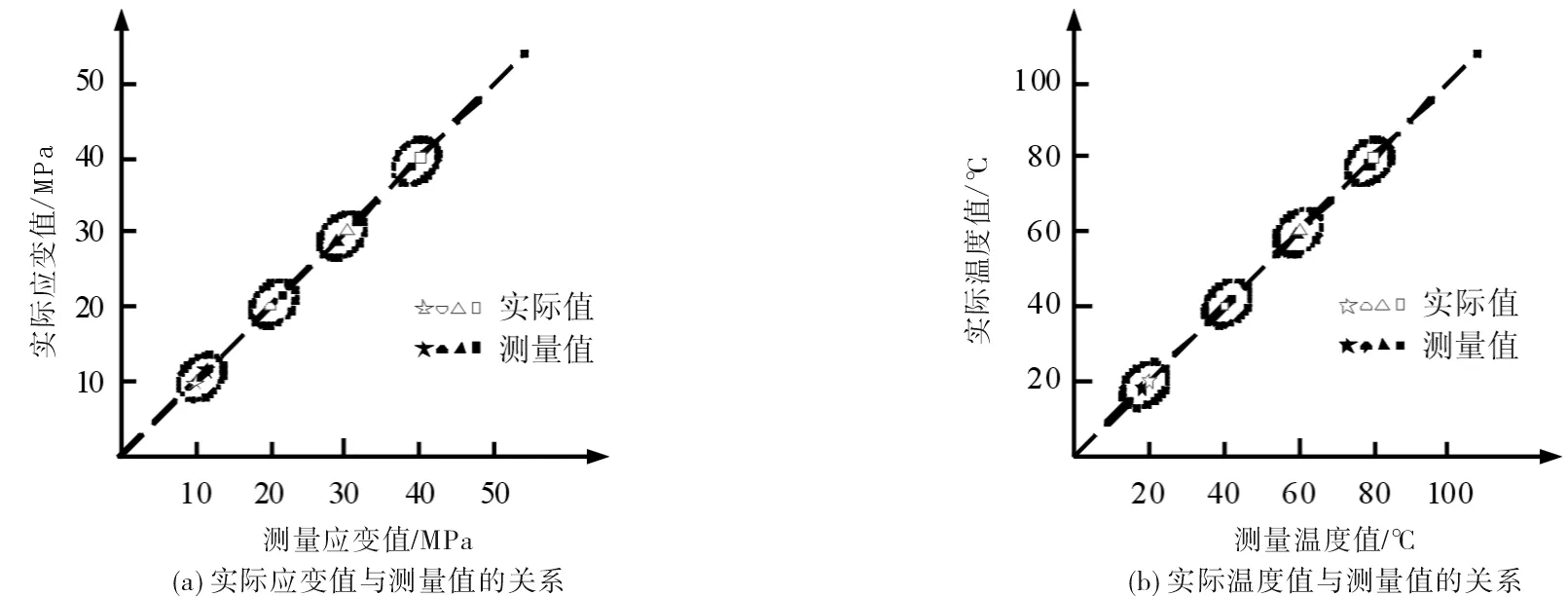
图5 实际值与测量值的关系曲线Fig.5 Relation between actual value and measured value

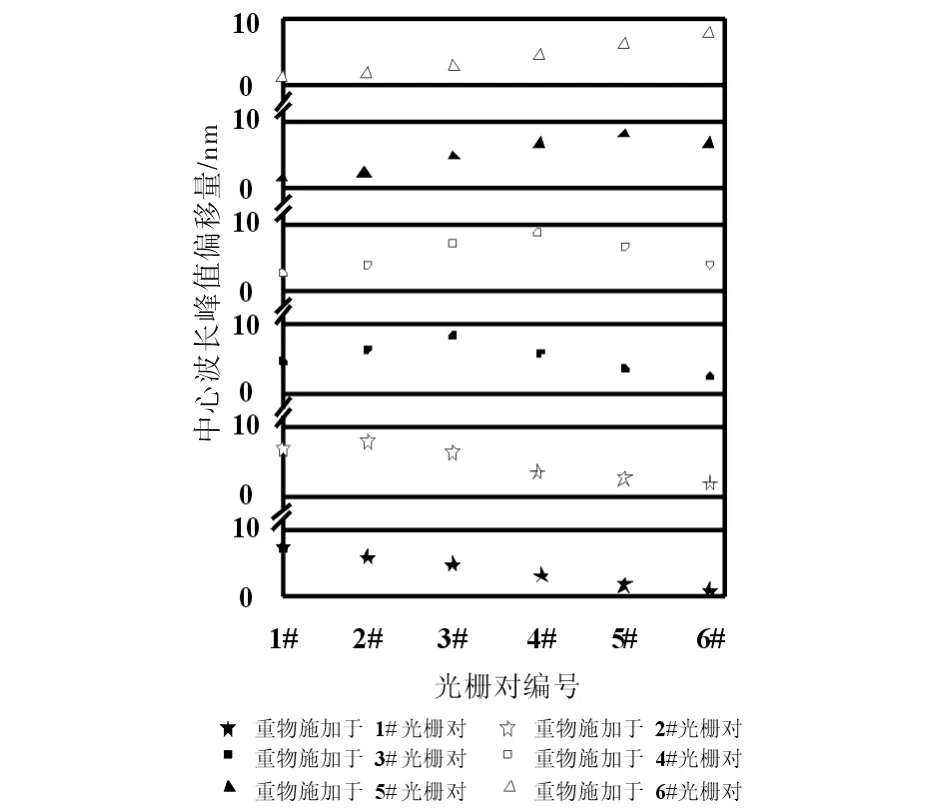
图6 准分布式光栅对中心波长偏移状态Fig.6 Center wavelength migration of quasi-distributed grating pairs

(2)通过实验测得的应变/温度数据较实际应变/温度值存在一定差异，一方面由于理论分析时认为两个Bragg光栅完全一样，具有相同的温度系统，但实际上略有差别；另一方面由于光栅的胶层涂覆也不尽相同.

(3)准分布式光栅应变点定位方法能够准确识别出重物应变施加位置，但定位精度与各光栅对之间的间隔有关，且当应变施加于两光栅对之间时，需要更加复杂的算法来确定其位置.

[1] 方祖捷, 秦关根, 瞿荣辉, 等. 光纤传感器基础[M].北京: 科学出版社, 2014: 58-64.

[2] Peng P C, Tseng H Y, Chi S. Long-distance FBG sensor system using a linear cavity fiber raman laser scheme [J]. IEEE Photonics Technology Letters, 2004, 16 (2): 575-577.

[3] Tan C H, Shee Y G, Yap B K, et al. Fiber Bragg grating based sensing system: Early corrosion detection for structural health monitoring [J]. Sensors and Actuators, A: Physical, 2015, 246 (8): 123-128.

[4] Singh D B, Suryanarayana G K. Application of fiber bragg grating sensors for dynamic tests in wind tunnels [J]. Indian Institute of Science, 2016, 96 (1): 47-52.

[5] 王 鑫, 王俊林. 光纤Bragg光栅应变、温度区分测量方法研究[J].光器件, 2012(5): 34-36.

[6] 李 薇, 侯 睿, 杨文俊. 基于温度减敏的光纤Gragg光栅应变传感器[J]. 仪表技术与传感器, 2013(5)：1-2, 6.

[7] 赵洪霞, 程培红, 鲍吉龙, 等. 一种两段式FBG应变和温度同步测量的实现[J]. 光电子·激光, 2014, 25(6): 1071-1074.

[8] 陈丽娟. 基于LPG-FBG级联结构的浓度和温度双参量测量系统[D]. 重庆: 重庆邮电大学, 2014.

[9] Wu Q, Okabe Y, Wo J. Fiber sensor based on interferometer and bragg grating for multiparameter detection [J]. IEEE Photonics Technology Letters, 2015, 27 (12): 1345-1348.

[10] Peng P C, Lin W P, Chi S. A self-healing architecture for fiber bragg grating sensor network [C]//IEEE. The 3rd IEEE International Conference on sensors. Vienna: IEEE, 2004:60-63.

[11] 叶 婷, 梁大开, 曾 捷, 等. 基于弓形梁增敏结构的FBG振动传感器研究[J]. 仪器仪表学报, 2012, 33 (1): 139-145.

TheImplementationofTwo-ParameterMeasurementofStrainandTemperatureUsingQuasi-DistributedFBG

LiWei,HouRui,ZhangZhijun

(College of Computer Sciences, South-Central University for Nationalities, Wuhan 430074, China)

In order to solve the cross sensitivity problem of strain and temperature measurement existing in Fiber Bragg Grating, a scheme that implement two-parameter measurement of strain and temperature by placing two FBG at upper and lower end face of a bearing beam is presented. This scheme can both overcome the restriction of traditional two-parameter measurement method and simplify the separation algorithm. Calibration and measurement experiments results indicated that the response curves of strain and temperature demonstrate good corresponding relationship in the range of 0～100℃ and 0～40MPa, and the maximum error is 3.7% and 4.2% respectively. This scheme is feasible to locate the position of strain point in quasi-distributed FBG, and has high application value.

quasi-distributed；FBG；two-parameter measurement

2016-09-02

李 薇(1982-)，女，讲师，博士，研究方向：新型传感器技术与应用，E-mail: liwei@mail.scuec.edu.cn

国家自然科学基金资助项目(61503418)；中央高校基本科研业务经费项目(CZY15008)

TP23

A

1672-4321(2017)04-0084-04