小学简易方程教学需要处理好的几个问题
刘东平
方程的学习是中小学数学的重要任务之一。小学阶段的简易方程教学虽然是初级内容,但却为后续代数学习提供准备和铺垫,是实现算术思维到代数思维转变的基础。聚焦小学简易方程教学所存在的问题,可大致概括为三个方面:什么是方程?怎样解方程?如何用方程解決问题?笔者结合“国培计划——送教下乡”活动中看到的真实情况展
开分析。
一、方程概念的教学
方程概念教学过程中,要让学生感知方程的意义,教师多以教材为范本“照葫芦画瓢”,没有适当的补充,所提供材料单一、缺少变化,致使学生对方程意义的感知过于肤浅,影响后续内容的学习。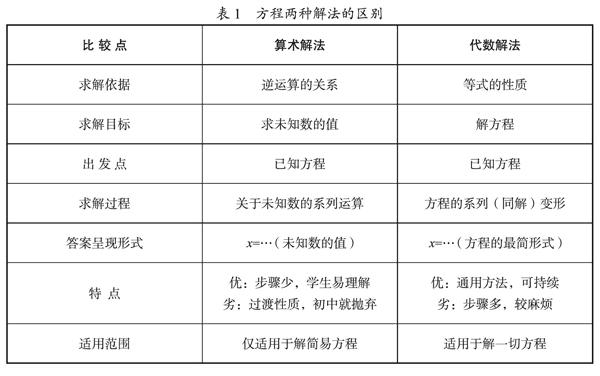
一个新数学概念的初次学习,既要让学生体会引入这个概念的必要,更要让其透过概念外在形式的丰富变化,发现概念内在不变的本质特征。方程概念的教学尤其需要如此,否则,学生在后续学习中,极易受习惯性“算术思维”的影响,出现诸如“连等式”的规律性错误。南京大学哲学系郑毓信教授给出了具体的教学建议:1.有意识地使用不同的字母,或是对已选定的字母做出改变,直至用更为复杂的符号表达式去取代原来的字母。如将4x+7=35变形为4y+7=35,进而改变为4(2r+1)+7=35,这有利于学生较为深入地认识方程的内在数学结构。2.由于方程之前的学习已经让学生形成思维定式:等号是有方向的,左边表示应做的运算,右边表示答案。要克服这一定式的消极影响,教师需要有意识地让学生构造这样一些等式,先是两边都有一个运算,如4+3=6+1,2×6=4×3,2×6=10+2等;接下来是每边都有两个运算的,随后是每边都有乘法的,如7×2+3-2=5×2-1+6等。这样有助于帮助学生初步地建立起“等号”的“结构性观念”,而不会只是认为“等号”就是“给出答案”。
此外,还需要进一步指出,等号右边的项不一定是单一的数,也可能是一个代数式,如23=x,46=2x,4y-2y=94-70,2x+140=94+4x等,帮助学生形成完整的方程概念。同时,还要利用学生初次认识方程的时机,发挥首次感知的强势效应,培养学生对方程的好感。如可以让学生通过判断一些稍微复杂的等式是不是方程的练习(注意这里仅判断是否是方程,无须考虑怎么解方程的问题),进而让学生认识到,方程可以有各种不同的形式,应用方程能解决很复杂的
问题。
二、解方程的教学
解方程应该用“逆运算的关系”,还是用“等式的性质”?关于这个问题,人教版《教师教学用书》(五年级上册)已经给出了明确的回答:从小学起引入等式的基本性质,并以此为基础导出解方程的方法;以等式的基本性质为基础,而不是依据逆运算的关系解方程。为了更好地理解和把握《课程标准的》精神及要求,需要清楚地了解两种解法的区别,并以此为依据对二者进行较为深入分析(见表1)。
从上述分析可以看出,运用“逆运算的关系”解方程的算术解法是学生已经习惯的算术思维方式,反映的是“过程性观念”;用“等式的性质”解方程的代数解法是学生陌生的代数思维方式,反映的
是(代数的)“结构性观念”。两种解法在思维方式和教学观念上存在根本的不同,而不仅仅是操作上的区别。小学师生更喜欢用逆运算的关系解方程,主要是因为其操作简便并且早已习惯。但是,如果在教学实践中对此听之任之,势必固化学生算术思维和过程性观念,造成今后代数学习的障碍。
例1.列式计算:甲是60,比乙的少20,乙是多少?
1.算术解法:(60+20)÷=200。由于需要逆向思考,不少学生会在“20应+还是-”“还应×是÷”上纠结,于是常出现以下3种错误解法:(60-
20)÷=100;(60-20)×=16;
(60+20)×=32。更糟糕的是,有的学生由于不能真正理解,碰到类似的题会一错再错,成为顽疾。
2.方程解法:设乙为x,列方程:x-
20=60,解方程:x=200。由于方程是顺向思考,学生容易理解,也不易出错。
例2.两袋面粉共重440千克,甲袋、乙袋分别吃了一些后,甲袋剩下,乙袋剩下,这时甲∶乙=8∶5,原来甲、乙各重多少千克?
这道题是云南省西双版纳州2014年小学六年级质量检测试题,曾让当年的小学毕业生统测成绩优秀率明显下降。究其原因,与教学中教师不能正确处理两种解法不无关系。
1.算术解法:甲∶8÷=12,
乙:5÷=10;12+10=22;
甲:440×=240(千克);乙:440×=200(千克)。
2.方程解法:设甲袋重x千克,则乙袋重(440-x)千克,
列方程:x∶(440-x)=8∶5;
解方程:x=240;440-x=200。
这道题数量关系较为隐晦复杂,算术解法简洁、巧妙,但学生理解不易,想到就更难。方程解法求解过程虽然较为烦琐,但理解容易,一般学生也可以掌握。事实上,在笔者听课的班级里也就只有一人给出了正确的算术解法;班里不少学生不仅列对了方程,而且其中的大部分学生也能正确地解方程。
从上述例题可以清楚地看到,用算术法解决问题虽然简便,但具有较大的局限:一是用算术法求解逆向思考的问题是许多学生的困难所在;二是算术法所能解决的都是数量关系比较简单的问题。相反,列方程解决问题却具有“变逆向思考为顺向思考”的优势,而且方程能解决数量关系复杂得多的问题。事实上,许多算术解法精巧的题,如果改用方程来解,就要自然、容易得多。
总之,小学阶段简易方程的教学担负着与初中代数衔接与过渡的任务,不能因为学生不习惯或嫌麻烦就降低对学生的要求,小学的算术思路及其算法掌握得越牢固,对中学代数起步教学的负迁移就越明显。南京大学郑毓信教授指出:“应当以代数思维作为小学算术教学的基本指导思想,努力促进学生由操作性观念向结构性观念转变。”
(作者单位:云南省西双版纳州景洪市教师进修学校)
责任编辑:李莎
lis@zgjszz.cnendprint

