酸压、生产一体化油管柱的力学分析

李 杰，丁艳艳，王丽荣，石善志，廖锐全，张慢来，张 琴

1长江大学石油工程学院，湖北 武汉2新疆油田公司工程技术研究院，新疆 克拉玛依3中石油气举试验基地多相流研究室，湖北 武汉4油气钻采工程湖北省重点实验室(长江大学)，湖北 武汉

酸压、生产一体化油管柱的力学分析

李 杰1,2，丁艳艳2，王丽荣2，石善志2，廖锐全1,3,4，张慢来3,4*，张 琴3,4

1长江大学石油工程学院，湖北 武汉2新疆油田公司工程技术研究院，新疆 克拉玛依3中石油气举试验基地多相流研究室，湖北 武汉4油气钻采工程湖北省重点实验室(长江大学)，湖北 武汉

一体化油管柱一次下井后完成酸压、生产等多种井下作业，节省了多次更换管柱的作业成本，且有效提高了作业效率。基于三维弯曲井眼中管柱的几何描述，建立考虑井身结构、管柱几何、物理特性和作业参数的管柱力学模型，分析一体化管柱在下入、酸压、生产等过程的力学特点，提出计算封隔器作用力的方法，确定了各过程中管柱的载荷、应力分布以及轴向变形，结合典型井参数得出酸压为管柱的最恶劣工况，井口处是管柱的最危险位置，最小安全系数1.75能满足强度要求。另外，各工况下管柱无正弦和螺旋变形发生，可判定管柱满足稳定性要求。通过该研究，建立了一体化油管柱的力学分析方法，给出封隔器作用力的计算步骤，从管柱的强度和稳定性两方面评价了管柱的安全性能，有利于保障一体化管柱的安全服役。

一体化管柱，力学分析，封隔器，强度，稳定性

1.引言

井下油管柱是油气从井底顺利到达井口的唯一通道，保证油管柱在各种外载荷下的强度安全性是实现油气正常开采的基本条件之一。一体化油管柱下入井筒后可以完成酸压、生产等多种井下作业，避免管柱更换所需的多次上提、下放，节省了施工成本，提升了作业效率，特别适合深井和超深井，已广泛应用在高压气田的开发中[1]。由于一体化油管柱经历了不同的作业过程，承受的载荷变化复杂，其安全性取决于最恶劣工况，需要对一体化管柱从下入井筒到生产整个作业过程进行详细的力学分析，以获得管柱的最危险工况和危险位置，从而为管柱的合理设计和安全应用提供理论指导[2]。当前，许多学者对井下管柱的屈曲行为进行了大量研究，建立了预测管柱发生正弦或螺旋屈曲等永久变形的临界条件，可用于判断管柱的平衡状态，为稳定性分析提供依据[3]。因此，拟在准确描述井眼轨迹和管柱结构的基础上，建立考虑众多因素的管柱力学计算模型，分析一体化管柱在各工况下的受力和变形特点，提出油管柱的力学计算方法和封隔器作用力计算步骤，从强度和稳定性两方面综合评价一体化油管柱的安全性，为其设计和安全应用提供科学依据。

2.力学模型的建立及求解

2.1.三维弯曲井眼中管柱的几何描述

管柱在井筒中常因外力发生失稳，出现正弦或螺旋的屈曲变形[4]，导致其轴线与井眼轨迹不再重合或平行。如图1所示，在法平面上，管柱轴线上C点相对于井眼轴线上的O点，有一偏离主法线的偏转角θ。假定弯曲失稳后管柱始终与井壁保持连续接触，则C点在以O点为圆心、半径为r的圆上，即：

或

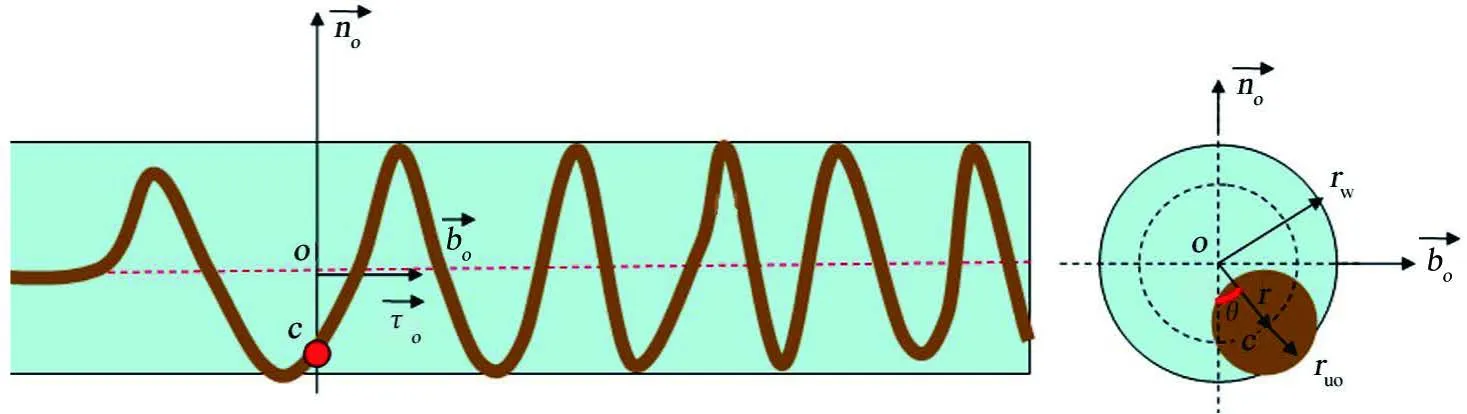
Figure 1.The geometric description of downhole tubing string图1.井下管柱的几何描述

2.2.管柱受力分析

管柱微元ds在井筒中的受力如图2所示。在单位长度上分布的外力矢量有：① 管柱自重(其中，q为管柱重量，N/m；为竖直方向的单位矢量，1)。② 弯曲管柱与井壁之间的接触正压力③ 流体黏滞摩阻力(其中，分别为管柱内、外的流体流动摩阻力，N/m；为井眼轴线的切向单位矢量，1)。④ 管柱与井壁之间的轴向摩擦力N/m (其中，f为管柱与1井壁之间的轴向摩擦系数，1)。⑤ 环向摩擦力N/m (其中，f为管柱与井2壁之间的环向摩擦系数，1)。

管柱微元体内、外侧壁上的流体压力为pi(s)、po(s)，Pa；其静力等效作用相当于分别在s和截面处作用有一对轴向压缩载荷(pi(s)Ai、po(s +ds)Ai)、拉伸载荷(po(s)Ao、po(s +ds)Ao)和一个分布载荷其中，Ai、Ao分别为管柱的内、外圆截面积，m2。

管柱微元在以上外力及内、外流体压力的作用下处于平衡状态，有平衡方程：

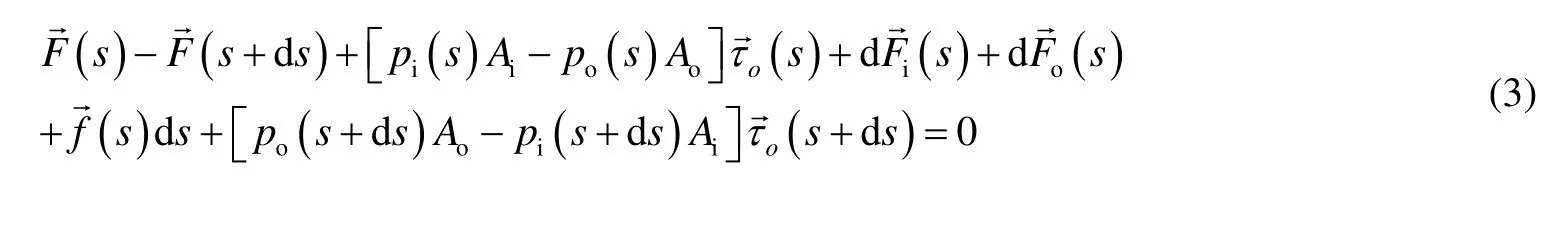
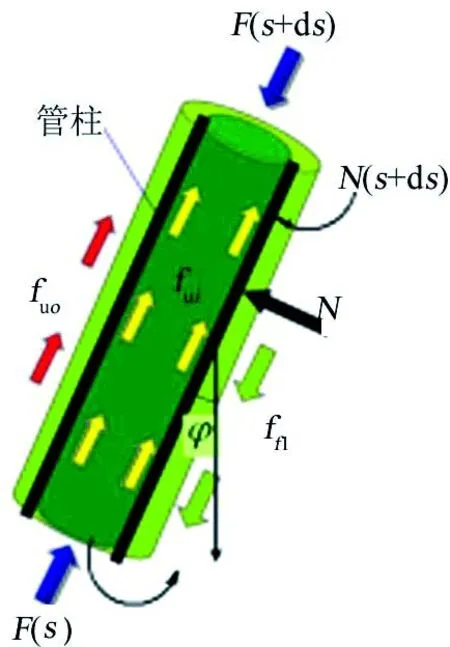
Figure 2.The force diagram of micro-element图2.微元体受力示意图

化简，得：

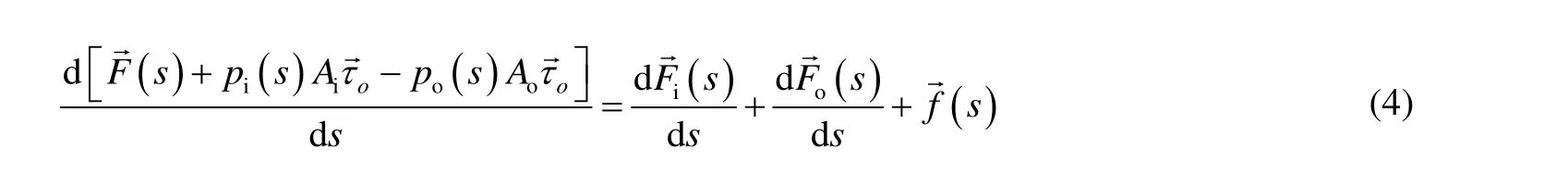
引入等效力：

则

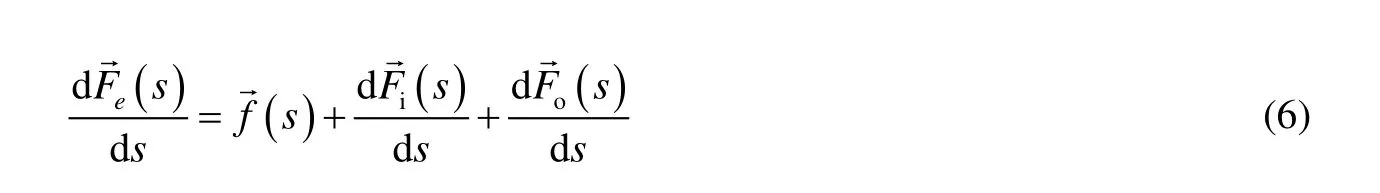
将单位长度上的外力代入式(6)，并沿oτ→投影，得管柱轴向力的平衡微分方程：

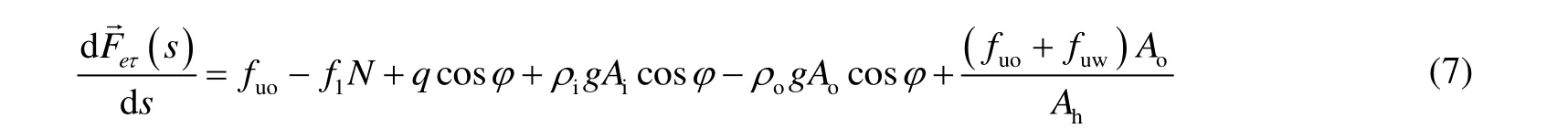
2.3.轴力计算

将总长为L的油管柱划分为n段，并从底端开始排列序号：0，1，…，n。根据方程(7)，利用差分方法可以确定j+1节点处的轴力为：

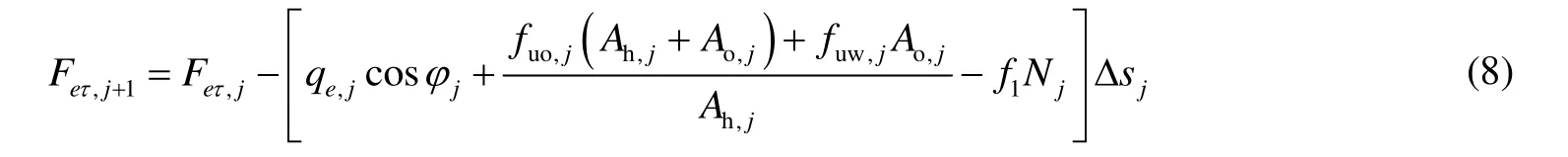
j节点处的真实轴力为：

节点j处管柱受到的正压力按下式计算：

其中：

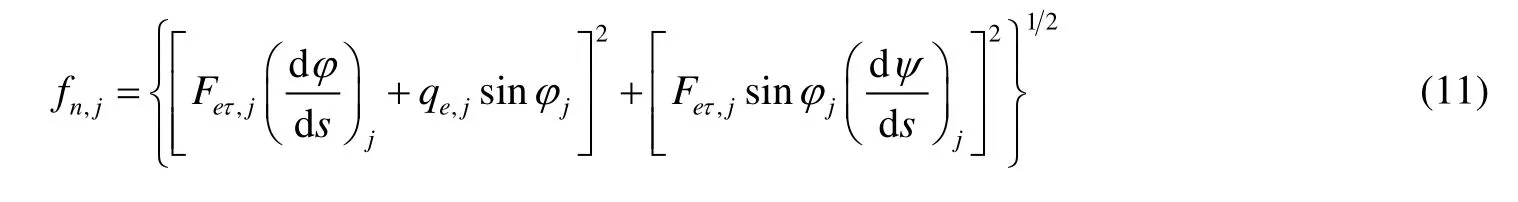
式中：Feτ,j、Feτ,j+1为第j个节点和第j+ 1个节点的轴力，N；Δsj为管柱微元长度，m；qe,j为管柱的等效线重，N/m；ψ为方位角，(˚)。

系数nj随无量纲轴力βj的取值不同，井下管柱处于不同的平衡状态：当βj< l时，管柱处于稳定状态；当1 <βj< 1.449时，管柱处于正弦屈曲状态；当βj> 1.449时，管柱处于螺旋屈曲状态[5]。

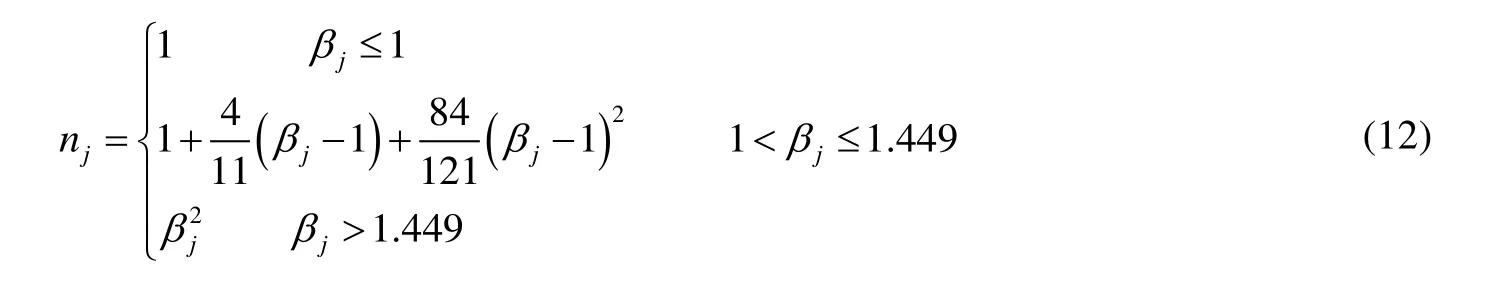
其中，

式中：Ej为节点j处管柱的弹性模量，Pa；Ij为节点j处的极惯性矩，m4；rj为节点j处的半径，m。

2.4.边界条件

利用式(8)自下而上迭代计算管柱上各点的轴向力时，需首先确定管柱底端及封隔器处的边界条件。

2.4.1.力边界条件

封隔器坐封时的受力情况如图3所示。封隔器随管柱下到预定位置后，投球封闭管柱下端，第一次加压使封隔器的卡瓦张开锚定在套管内壁上(图3(a))，有：

在管柱下入过程中，管柱端部不封闭，则pi=po，有：

式中：Fe,0为一次憋压封隔器受力，N；Ao、Ai分别为与封隔器相接的作业管柱的内、外横截面积，m2；Apo、Api分别为封隔器密封筒的内、外横截面积，m2；Fo为封隔器上部受到的真实轴力，N；po、pi分别为管柱内、外流体压力，Pa。

当封隔器坐封后，油管内压力变化(二次憋压)引起的管柱变形已经受到限制，封隔器组(包括卡瓦、水力锚、胶筒等)将对封隔器密封筒产生作用力(图3(b))，则

式中：Fe,1为二次憋压封隔器受力，N；Fp为封隔器作用力，N。

由式(11)～(14)可以看出，在封隔器坐封前及一次憋压过程中，等效力为0，管柱不会发生屈曲，在生产和酸压过程中，等效轴力考虑了“虚构力”当内压远大于外压时，在管柱下部可能发生在酸压、生产过程中，封隔器处的受力如图3(c)所示，有：屈曲变形。另外，由于Fp未知，需根据封隔器处的位移边界条件来确定。

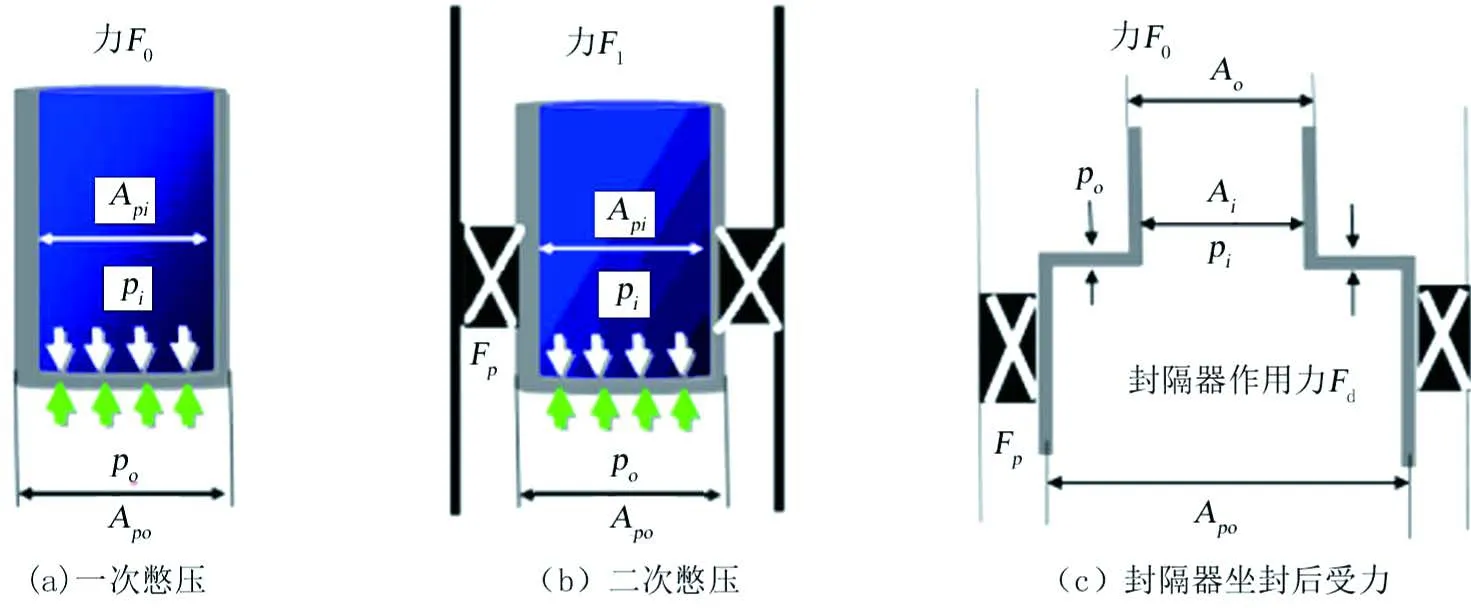
Figure 3.The setting force of the packer图3.封隔器坐封时的受力

2.4.2.位移边界条件

封隔器坐封后，由于二次憋压、酸压或生产过程中温度、压力的变化，封隔器上方的管柱变形发生变化，引起封隔器处管柱的位移。对于带插管或只带卡瓦的封隔器管柱，管柱只能上移，但不能下移；对于不能移动的封隔器，该处的管柱被固定。这些被限制的位移都将转化为各工况下封隔器的作用力。因此，以坐封状态为基准计算管柱的变形变化量，记为：式中：L0为坐封后初始状态的管柱长度，m；L1(s)为坐封后酸压、生产等工况下轴力产生的轴向变形，m；L2(s)为管柱弯曲产生的轴向变形，m；L3(s)为管柱内外压产生的轴向变形，m；L4(s)为温度产生的轴向变形，m。

封隔器对油管的作用力Fp按下面步骤进行迭代计算：

1) 假设封隔器作用力Fp为0，根据公式计算轴向变形变化总量，此时不等于0。

2) 由于台阶存在，这个变形变化量 ∆L实际上是不可能发生的(图4)，令

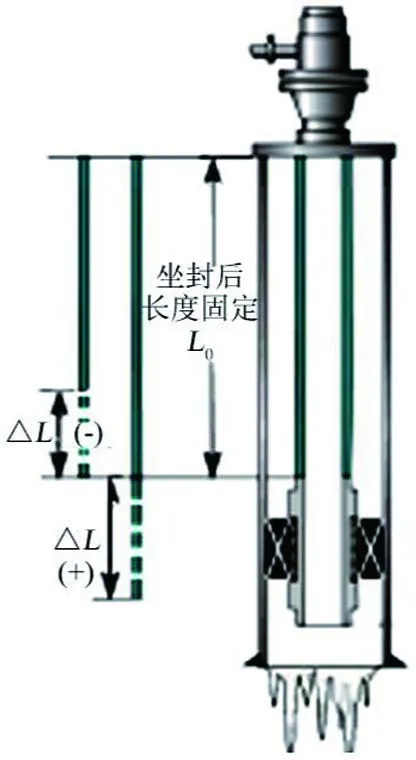
Figure 4.The deformation diagram of the pipe string above the packer图4.封隔器上方管柱的变形示意图

4) 若 ∆L(s)不等于0，修正F为

p

3.典型算例计算及分析

3.1.已知条件

B101井的三维井眼轨迹如图5所示。一体化油管柱规格为∅88.9 mm × 6.45 mm，材料和钢级分别为G3、125，线重为13.7 kg/m，屈服强度为862 MPa。油管柱下深5020 m，套管内、外径分别为152.5 mm和177.8 mm，封隔器坐封深度4966 m。不同作业的压力和温度参数如表1和表2所示，温度和压力随垂深的增加按线性增大。

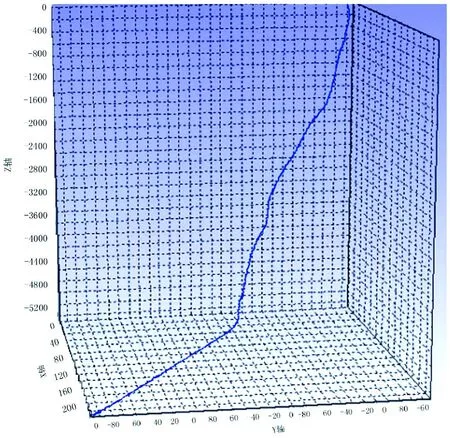
Figure 5.3D well traiectory of B101 well图5.B101井的三维井眼轨迹

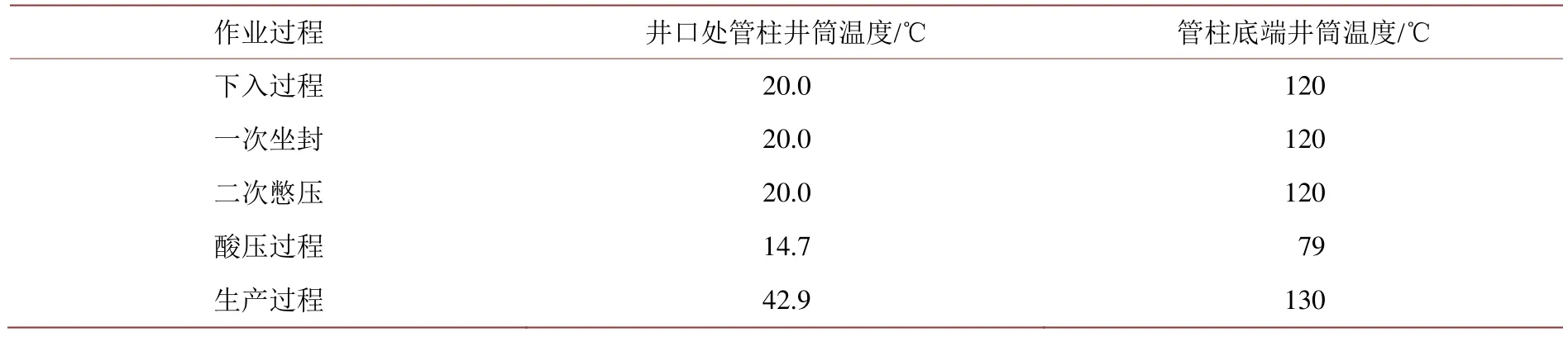
Table 1.The calculation results of wellbore temperature表1.井筒温度计算结果

Table 2.Calculation results of wellbore pressure表2.井筒压力计算结果

3.2.载荷、变形及应力分析

油管的轴向应力和等效应力(第四强度理论)分布如图6所示，油管柱在井口处的载荷及不同作业过程中的变形、强度校核结果如表3～5所示。

由图 6(a)可见，在下入井筒、一次坐封、二次憋压、酸压增产、生产过程中，油管柱的轴向应力沿着井深方向基本呈线性递减变化，到达一定深度以后，该点处的管柱轴向应力降为 0，则该点以上管柱受拉，以下部分受压。由图 6(b)可见，按第四强度理论计算的等效应力为三向应力，受周向、径向应力及急剧变化的狗腿度(约井下4800 m)影响，生产过程中呈曲线分布。油管柱的最大轴向应力和等效应力均出现在井口处，管柱在井口处的安全系数最小，是受力的最危险位置。

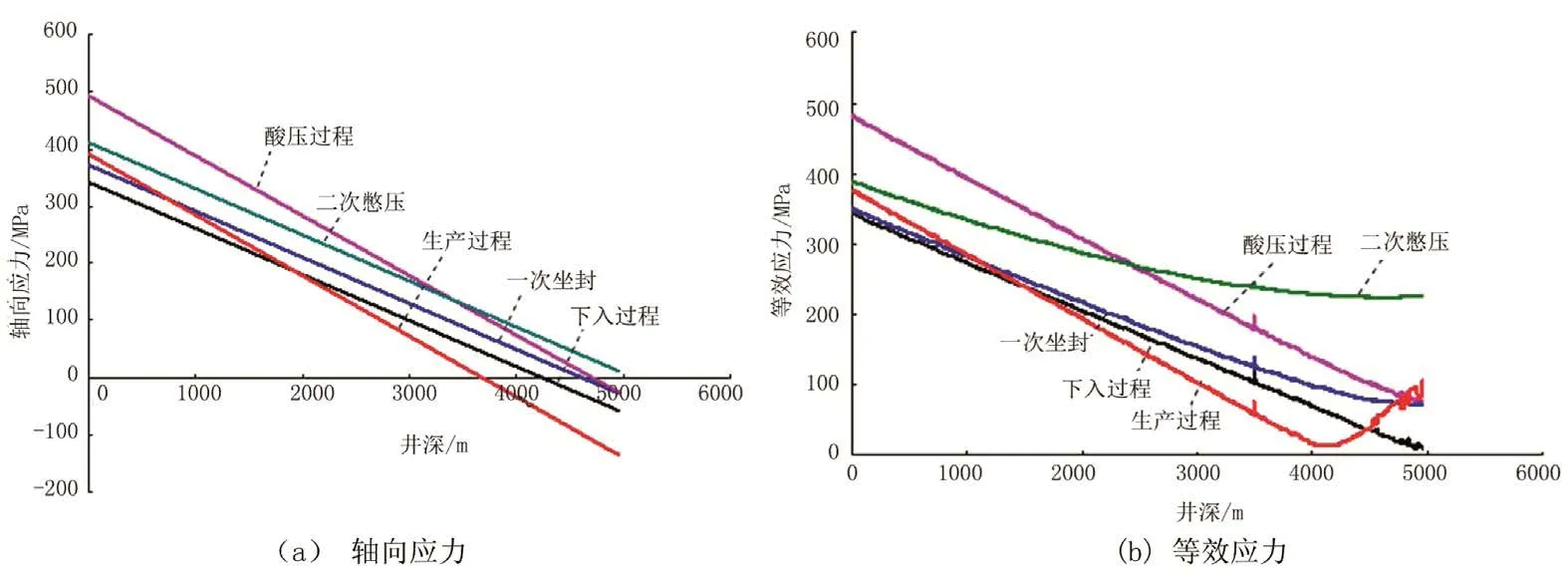
Figure 6.The axial and equivalent stress distributions of tubing string in different operation processes图6.不同操作过程中油管柱的轴向、等效应力分布

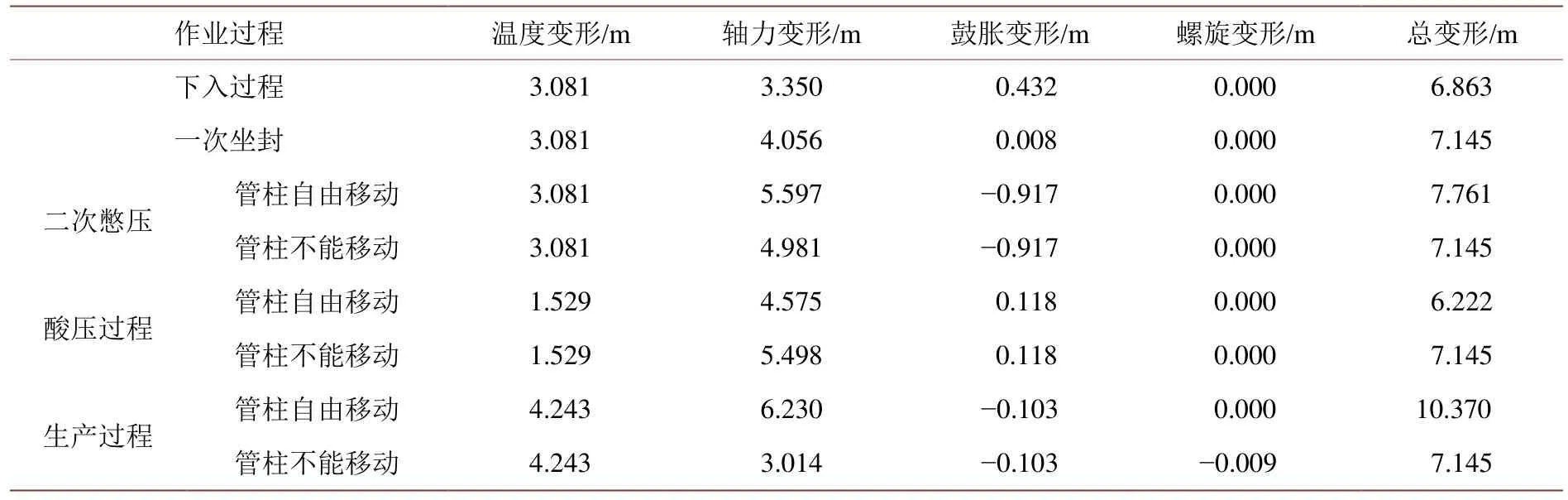
Table 3.The axial deformations of tubing string表3.管柱轴向变形

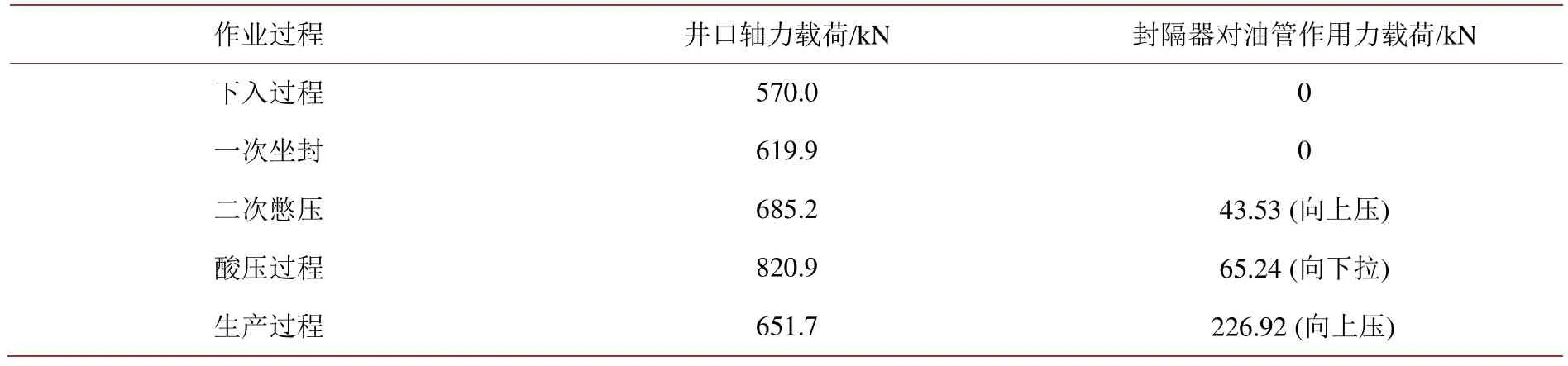
Table 4.The load of tubing string表4.管柱载荷

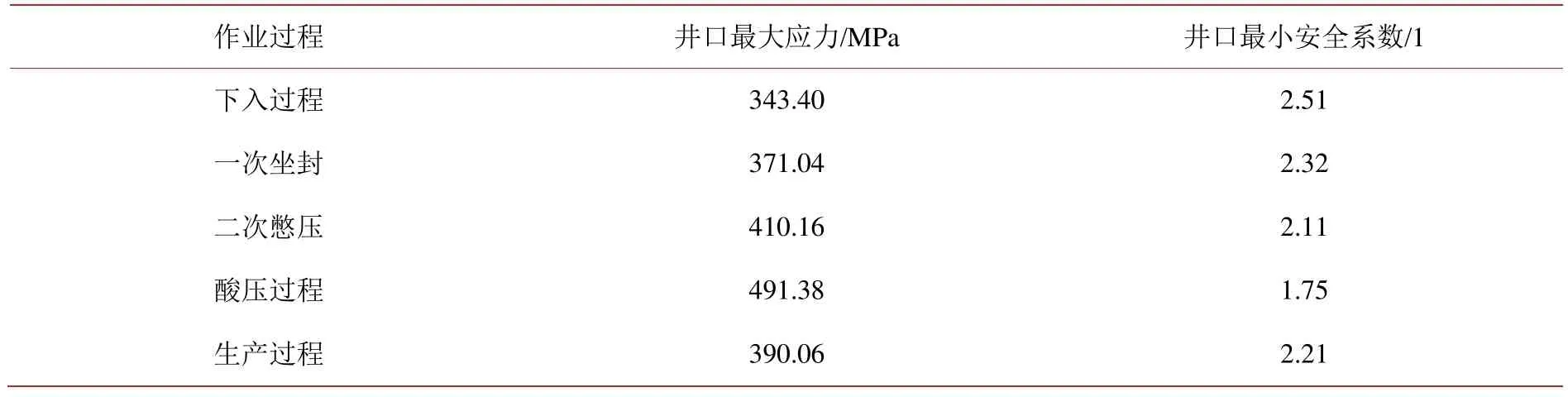
Table 5.The maximum stresses and minimum safety factors of tubing string表5.管柱的最大应力及最小安全系数

由表 3、表 4可看出，油管内的压力显著影响管柱的变形和应力大小。由于压力增大导致管柱的鼓胀变形增加，管柱轴向缩短，封隔器对上部管柱产生较大的向下拉伸力，增大了管柱在井口处(危险位置)应力，使最小安全系数下降，因此，具有较大作业压力的酸压是一体化油管柱的最恶劣工况，需重点对该工况下的管柱安全性进行分析。目前投入使用的一体化油管柱在不同作业过程中的最小抗屈服安全系数高于1.75 (表5)，无正弦和螺旋变形发生，可以满足酸压、生产联作的安全要求。

4.结论

基于三维弯曲井眼中管柱的几何描述，建立了考虑井身结构、管柱几何、物理特性和作业参数的管柱力学模型，根据一体化油管柱的工作特点，提出了封隔器作用力的详细计算过程，形成一体化油管柱的力学计算方法，确定了B101井在不同工况下的油管柱变形和应力，进行了强度和稳定性评价。研究表明，井口处的管柱安全系数最低，酸压过程相对于管柱下入和生产工况，管内的作用压力较高，使得油管柱的最小安全系数从下入工况时的2.51大幅下降至1.75，基本满足强度要求；同时，油管柱在各工况下无正弦和螺旋等永久变形发生，预示油管柱是稳定的。通过该研究，为一体化油管柱的设计和应用提供了科学依据，有利于保障井下管柱的安全。

References)

[1]孔凡群, 王寿平, 曾大乾.普光高含硫气田开发关键技术[J].天然气工业, 2011, 31(3): 1-4.

[2]曹言光, 张庆生, 陈传东, 等.普光水平井投产一体化管柱及参数优化[J].石油钻采工艺, 2016, 38(5): 667-671.

[3]郑永刚.管柱在井内弯曲失稳的研究[J].钻采工艺, 1992, 15(1): 40-45.

[4]高国华, 李天太, 李琪, 等.钻柱在水平井眼中的正弦屈曲[J].西南石油学院学报, 1994, 9(2): 37-40.

[5]高国华, 李天太, 李琪, 等.考虑摩擦时水平井钻柱的稳定性分析[J].西南石油学院学报, 1995, 10(3): 31-34.

The Mechanic Analysis of Integrated Tubing String for Acid Fracturing and Production

Jie Li1,2, Yanyan Ding2, Lirong Wang2, Shanzhi Shi2, Ruiquan Liao1,3,4,
Manlai Zhang3,4*, Qin Zhang3,41School of Petroleum Engineering, Yangtze University, Wuhan Hubei2Research Institute of Engineering Technology, Xinjiang Oilfield Company, Petro China, Karamay Xinjiang3Multiphase Flow Research Laboratory of Gas Lift Test Base (Yangtze University), CNPC, Wuhan Hubei4The Branch of Key Laboratory of CNPC for Oil and Gas Production, Wuhan Hubei

May 30th, 2017; accepted: Jun.7th, 2017; published: Dec.15th, 2017

The integrated tubing string saved the operation cost of replacing the pipe string and increased the operation efficiency as it could complete plenty of down hole operations such as acid fracturing and production.Based on the geometrical description of the pipe string in the 3D curved borehole, a mechanical model of pipe string considering wellbore structure, string geometry, physical characteristics and operation parameters was established, and the calculate method for the packer force was presented by analyzing the mechanical characteristics of the integrated pipe string in the process of its running down, acid fracturing and production.The load, stress distribution and axial deformation of the tubing string were determined in each process.The result shows that the fracturing is the worst working condition to the tubing string and the wellhead is the most dangerous position, and the intensity requirements can be met with the minimum safety coefficient of 1.75.Furthermore, the tubing string is stable as sinusoidal or spiral deformation is not appeared in all working conditions.Through the research, the mechanical analysis method of the integrated tubing string and the calculation steps of packer force are given, and the safety performance of the tubing string is evaluated with its strength and stability.The results of the study are beneficial for the security service of the integrated tubing string.

Integrated Tubing String, Mechanical Analysis, Packer, Strength, Stability

*通信作者。

文章引用:李杰, 丁艳艳, 王丽荣, 石善志, 廖锐全, 张慢来, 张琴.酸压、生产一体化油管柱的力学分析[J].石油天然气学报, 2017, 39(6): 79-88.

10.12677/jogt.2017.396101

Copyright © 2017 by authors, Yangtze University and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).http://creativecommons.org/licenses/by/4.0/

李杰(1982-)，男，硕士生，高级工程师，现主要从事油气田开发和科研管理工作。

2017年5月30日；录用日期：2017年6月30日；发布日期：2017年12月15日

国家科技重大专项(2016ZX05056004)；国家自然科学基金(61572084)；湖北省教育厅科学研究计划项目(B2016032)。

[编辑]帅群