基于蒙特卡罗方法的密度测井薄层影响分析

刘伟男，邓 瑞*，汪 鹏，钱博文，秦承运1油气资源与勘探技术教育部重点实验室(长江大学)，湖北 武汉长江大学地球物理与石油资源学院，湖北 武汉中国石油大学(北京)地球物理与信息工程学院，北京

基于蒙特卡罗方法的密度测井薄层影响分析

刘伟男1,2，邓 瑞1,2*，汪 鹏3，钱博文1,2，秦承运1,21油气资源与勘探技术教育部重点实验室(长江大学)，湖北 武汉2长江大学地球物理与石油资源学院，湖北 武汉3中国石油大学(北京)地球物理与信息工程学院，北京

薄层是影响密度测井的重要因素，利用蒙特卡罗方法对密度测井进行数值模拟，获取密度测井对薄层的响应资料，用于研究薄层对密度测井的影响，确定密度测井记录点及计数率曲线变化规律。研究表明，对于低密度薄层，随着薄层纵向位置的移动，计数率先增大后减少，曲线形态对称，极大值点为记录点；对于高密度薄层，随着薄层纵向位置的移动，计数率先减少后增大，曲线形态近似对称，极小值点为记录点。同时针对密度测井最小纵向分辨率进行了讨论。

密度测井，蒙特卡罗方法，薄层，对称，最小纵向分辨率

1.引言

随着石油勘探开发中面对的地层越来越复杂，薄层在油气资源的勘探开发中变得越来越重要。在对薄层滚动勘探开发逐渐深入的过程中[1]，薄层密度测井解释评价所遇到的难点越来越突出，主要表现为受环境和围岩影响，难以反映地层的真实情况，造成了评价工作难度加大，参数求取不准，测井符合率不高，对油藏后续勘探开发影响较大[2]。

笔者运用蒙特卡罗方法对密度测井进行数值模拟，获取对薄层的响应资料，并对其影响因素进行综合分析，以提高校正准确度，为油藏综合评价以及测井综合解释提供准确的密度测井资料。

2.模拟物理模型

密度测井也称为伽马–伽马测井，是利用同位素伽马放射源向地层中辐射伽马射线，然后用与放射源相距一定距离的探测器测量从地层来的经过散射和吸收的伽马射线。中能伽马射线辐射在地下岩石中主要发生康普顿效应，它的散射截面与地层的体积密度密切相关，因此可用来测量地层岩石密度。密度测井仪器主要由伽马源、屏蔽材料、探测器和仪器骨架组成[3]。

利用蒙特卡罗程序MCNP建立密度测井地层模型。根据密度测井的实际工作条件(密度测井仪器贴井壁测量)，建立半圆柱地层模型(图1)，井眼也为半圆柱。模型高277 cm，地层半径10～43 cm，被划分成高6 cm、环距3 cm的相邻栅元。密度测井仪器紧贴井壁，仪器外壳厚5 mm，源仓材料是钢，伽马射线探测器外壳为铍(Be，密度为1.98 g/cm3)。铯-137(137Cs)伽马源点放在点(9,0,54)上，距下屏蔽体1 cm，距上屏蔽体1 cm，距井壁1 cm [4]。

该次研究采用的密度测井仪器是长源距仪器，长源距探测器(源距40 cm)放在点(9,0,94)。井眼中伽马源下部、伽马源与长源距探测器之间以及长源距探测器上部，均充满屏蔽体[5]。半圆柱体外部是真空。模拟计算过程中，使用了光子重要性函数、权重窗口和能量截断等减方差以及其他优化算法[6][7]，大大缩短了MCNP的运行时间。

3.蒙特卡罗模拟结果及分析

3.1.低密度薄层

低密度薄层，薄层为孔隙度40%、饱含水的石灰岩(密度为2.026 g/cm3)，围岩为纯灰岩(密度为2.71 g/cm3)。把薄层从模型的底部逐渐向顶部移动，观察探测器计数率(光子通量/粒子数)的变化情况，计数率极大值的地方就是探测器最灵敏的探测区域。将厚度为54、45、36、18、9 cm的薄层从地层的底部逐渐向顶部移动，每次移动18 cm。探测器的能量箱只记录能量位于0.15 MeV和0.7 MeV之间光子的通量。该次研究分别计算了不同厚度薄层在不同位置时探测器计数率的变化，通过数据分类，可以得到探测器计数率随薄层位置变化的关系曲线[8]。

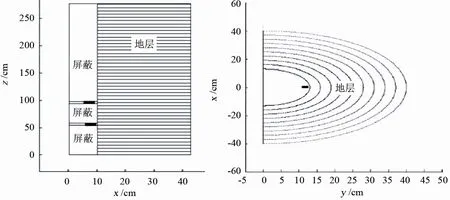
Figure 1.The density logging model based on Monte Carlo method图1.基于蒙特卡罗方法的密度测井模型

图2显示厚度分别为9、18、36、45、54 cm的低密度薄层在地层纵向上移动时，长源距探测器计数率的变化曲线，近似正态分布。从图2中可以看出，拟合曲线极大值的位置在薄层纵向位置74 cm左右，探测器对薄层的响应曲线是左右对称的，对称点也是极大值点；也就是说，密度测井仪器对薄层的灵敏探测位置在74 cm左右的区域，而该位置恰好是长源距探测器和伽马源之间的中点。由于密度测井的数据处理是以长源距探测器计数率为主，从而在理论上验证了密度测井的灵敏探测位置是伽马源与探测器正中间的位置。从图2中还可看出，探测器计数率随着薄层厚度的增加，灵敏探测位置计数率数值变化越来越小，说明随着地层厚度的增加，计数率越来越接近原状地层计数率，受薄层影响越来越小。当薄层厚度增加到45 cm时，计数率最大值趋于稳定，说明该次研究模拟所用参数的密度测井仪器最小纵向分辨率约为45 cm [9]。

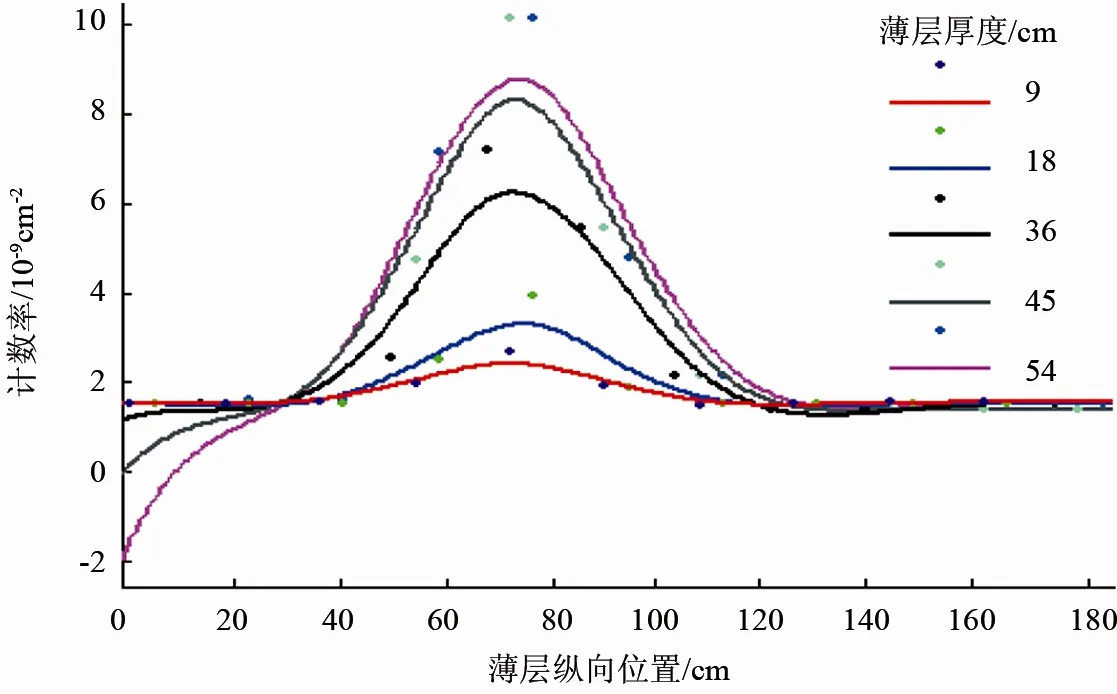
Figure 2.The response curve of long spaced detector counting rate changing with the position variation of low density thin layer with different thicknesses图2.长源距探测器计数率随不同厚度低密度薄层位置变化的响应曲线

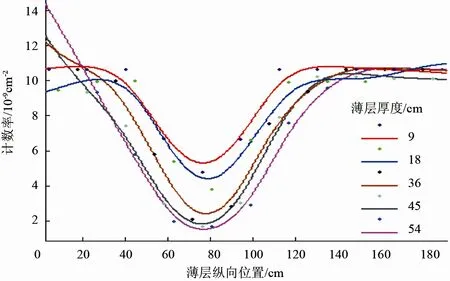
Figure 3.The response curve of long spaced detector counting rate changing with the position variation of high density thin layer with different thicknesses图3.长源距探测器计数率随不同厚度高密度薄层位置变化的响应曲线

3.2.高密度薄层

将低密度薄层改为高密度薄层，即将地层模型中的围岩换成孔隙度40%、饱含水的石灰岩(密度2.026 g/cm3)，而薄层换成纯灰岩(密度2.71 g/cm3)。从图3中可以看出，曲线近似对称分布，曲线变化规律是先减小后增大，同时对称点为极小值点，且极小值点在74 cm左右，为模型的伽马源与长源距探测器之间的中点，即灵敏探测位置在74 cm左右探测区域；同时，随着薄层厚度的增加，灵敏探测位置的计数率变化越来越小，当薄层厚度为45 cm时，计数率最小值趋于稳定，因此最小纵向分辨率约为45 cm。

4.结论

1) 低密度薄层在响应曲线上出现极大值，薄层厚度越大，极值越大；高密度薄层在响应曲线上出现极小值，薄层厚度越大，极值越小。对于长源距(40 cm)，其极值在74 cm处，大致位于伽马源与探测器之间的中点。

2) 对于最小纵向分辨率的研究表明：当薄层越薄时，其受到周围环境的影响较大，相对于地层真实值偏差较大；随着薄层变厚，受到的影响减小，偏差值变小。该次研究条件下的最小纵向分辨率约为45 cm。

References)

[1]王凤山, 霍广君, 冯立.发展应用薄差油层开采技术有效利用大庆油田地下资源[J].资源∙产业, 1999, 4(10): 22-24.

[2]程昆, 程仲, 吴文彦.一种薄层密度测井校正方法[J].测井技术, 2007, 31(6): 537-540.

[3]黄隆基.核测井原理[M].东营: 石油大学出版社, 2000.

[4]吴文圣, 肖立志.三探测器密度测井仪器的源距优化[J].核技术, 2010, 33(11): 849-853.

[5]吴文圣.三探测器密度测井的薄层影响及校正[J].天然气工业, 2003, 23(3): 38-40.

[6]李新梅.蒙特卡罗粒子输运模拟中源偏倚和网格权窗方法研究[D]: [硕士学位论文].合肥: 合肥工业大学, 2015.

[7]郭生良.γ能谱的蒙特卡罗计算方法探讨与模拟软件设计[D]: [硕士学位论文].成都: 成都理工大学, 2008.

[8]Briesmeister, J.F.(1985) MCNP-A General Monte Carlo Code for Neutron and Photon Transport.Version 3B, Los Alamos Radiation Transport Group, 1-200.

[9]洪有密.测井原理与综合解释[M].东营: 中国石油大学出版社, 2007: 10-15.

The Effect of Density Logging on Thin Layer Based on Monte Carlo Method

Weinan Liu1,2, Rui Deng1,2*, Peng Wang3, Bowen Qian1,2, Chengyun Qin1,21Key Laboratory of Exploration Technologies for Oil and Gas Resources (Yangtze University), Ministry of Education,Wuhan Hubei2School of Geophysics and Oil Resources, Yangtze University, Wuhan Hubei3School of Geophysics and Information Engineering, China University of Petroleum (Beijing), Beijing

Oct.26th, 2016; accepted: Dec.20th, 2016; published: Dec.15th, 2017

Thin layer was an important factor influencing the density logging.Monte Carlo method was applied to simulate the density logging and get the data of density logging response of thin layer, by which the influence of thin layer on the density logging was studied to determine the density logging record point and the change rules of the counting rate curve.The research indicates that the counting rate of low density thin layer increases initially and then decreases with the longitudinal movement of the thin layer.The shape of the curve is approximately symmetrical and the maximum point is a recorded point, while for the high density thin layer, the counting rate decreases first and then increases with vertical movement of the thin layer, the shape of the curve is also approximately symmetrical and the minimum point is the recorded point.Meanwhile, the minimum vertical resolution of density logging is discussed in this paper.

Density Logging, Monte Carlo, Thin Layer, Symmetry, Minimum Vertical Resolution

*通信作者。

文章引用:刘伟男, 邓瑞, 汪鹏, 钱博文, 秦承运.基于蒙特卡罗方法的密度测井薄层影响分析[J].石油天然气学报,2017, 39(6): 55-59.

10.12677/jogt.2017.396098

Copyright © 2017 by authors, Yangtze University and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).http://creativecommons.org/licenses/by/4.0/

刘伟男(1995-)，男，主要从事核测井模拟工作。

2016年10月26日；录用日期：2016年12月20日；发布日期：2017年12月15日

油气资源与勘探技术教育部重点实验室(长江大学)开放基金资助项目(K2016-14，K2016-15)；长江青年基金资助项目(2015cqn31)。

[编辑]龚丹