励磁系统与负荷相互作用对系统暂态稳定的影响
民航内蒙古空管分局 李楠
励磁系统与负荷相互作用对系统暂态稳定的影响
民航内蒙古空管分局 李楠
本文将随机响应面法(SRSM)应用于综合负荷模型及参数的不确定性分析中,就发电机不同模型及励磁系统参数与负荷参数相互作用对电力系统动态仿真稳定性的影响展开讨论,对如何提高模型和参数的精确性,更好进行电力系统安全稳定分析借鉴意义。
电力系统仿真;励磁系统;负荷模型
0 引言
现代电网的规模随着经济的发展也快速膨胀起来,而且国际间电网互联也不断增加。大电网因为拥有大量新式设备且结构复杂,其动态行为也难以预测,一个小事故就有可能波及到整个电网。因此关于电力系统安全稳定分析对电网的安全运行有很大的影响,提高模型和参数的精确性具有重要意义。由于负荷的随机性、大量性、多样性、分散性等特点,通常在实际的电力系统中使用建模的方法。由于大量不确定性存在于实际系统中,且发电机作为电网中最主要的设备之一,所以其模型以及励磁系统的关键参数又较大程度上影响着系统的暂态稳定性。综上所述,有必要在发电机模型以及励磁系统参数变动的背景下认真研究负荷模型和参数的不确定性。
1 随机响应面法
建立输入参数与输出响应之间的函数关系是随机响应面法基本思想。主要分为三个步骤:1)将输入参数用一系列标准随机变量表示(随机变量的标准化);2)将感兴趣的输出响应用标准随机变量组成的多项式来表示;3)选择合适的输入参数值来估计前面建立的多项式系数。这样就确定了响应的多项式,可以方便计算响应的方差、期望值、概率密度等统计信息,进行不确定度分析。

表1 发电机使用旋转直流励磁系统时的应用
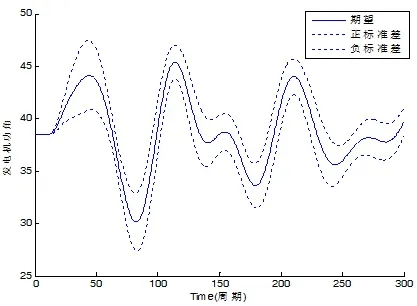
图1 100%无功负荷情况下的功角不确定性

图2 50%无功负荷情况下的功角不确定性
例如IEEE39节点系统,对潮流较重的线路5-6设置三相短路故障,用随机响应面法2阶模型定量分析当静态模型比例α和负荷动态电动机比例Kpm服从不同的分布,且负荷无功水平分别为50%、100%情况时,讨论其不确定性对发电机功角的影响。负荷模型采用感应电动机并联静态模型。静态负荷模型如公式如下所示,α=0时为恒功率模型;α=1时,静态负荷模型为恒阻抗模型。
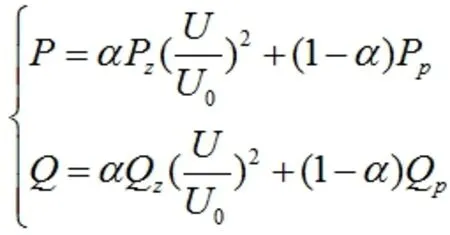
2 发电机使用旋转直流励磁系统时的应用
采用直流发电机作为励磁电源的励磁方式称为直流机励磁。优点是厂用电率较低(与无励磁机系统比较)。缺点是功率过大时制造上有一定困难,这是因为直流励磁机有整流环。对系统进行故障仿真,得到相应数据,见表1。
比较磁链恒定和加入直流励磁系统时的故障功角情况,可以发现,由于励磁系统可以控制并列运行各发电机间无功功率分配,所以无功负荷水平的降低,并没有过多的影响到负荷不确定性对于系统暂稳性的作用。此外,比较发电机采用经典模型时、发电机使用旋转直流励磁系统时的不确定性功角曲线情况,可以发现当采用经典模型时,在无功下降的情况下,±标准差曲线出现了一定程度的畸变,甚至相较功角期望值出现了反方向摆动,见图1~图2,而加入直流励磁装置后,这种情况便得到了较明显的改善,见图3~图4。

图3 100%无功负荷+直流励磁系统下的功角不确定性

图4 50%无功负荷+直流励磁系统下的功角不确定性
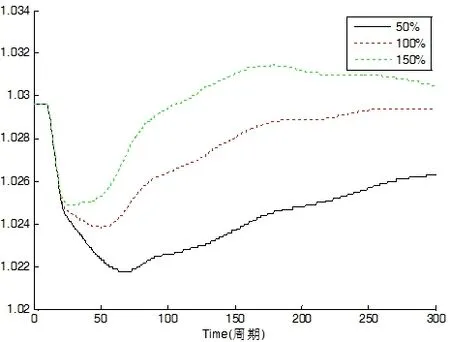
图5 KA摄动情况
3 励磁参数对功角不确定性的影响
众所周知,励磁器的调节作用会在一定程度上提高系统的暂态性能。大体上说,有两种方法可以提高暂态稳定性:增大减速面积和减小加速面积。发电机内电势Eq’通过励磁系统的调节作用,在故障切除后会迅速上升,并且功率输出提高,达到了增加减速面积的目的。下面讨论连续、旋转直流励磁系统参数对系统功角不确定性的影响。
3.1 连续、旋转直流励磁系统的关键参数
采用摄动法,就各参数变动对系统暂态稳定性的影响进行比较。具体做法是系统发生三相短路故障情况下按给定参考数据的50%、100%、150%变动励磁系统特定参数,考察其对平衡节点缓冲机39磁链的影响并绘制图形。
由图5可知,KA越大,故障后磁链恢复的速度以及幅度越大,理论上说越有利于系统暂态稳定。但进一步观察发现,取+100%的数据时,磁链很快恢复并超过了原来稳态时的值,然后再回落,所以有可能造成磁链的振荡。
由图6可以看出,TE的变化会对磁链恢复产生一定影响。较小的取值能拥有较快的恢复速度,但故障时磁链跌落也较严重。较大的取值在故障时跌落程度十分严重,且恢复速度欠佳。而采用系统原参数时,兼顾了上升速度以及幅度两方面的因素,可视为最佳选择。
通过陆续的摄动图形比较,可以发现KA、TE对磁链的影响相对较大,而TA、KF、TF这三个参数对励磁器输出的影响并不是十分显著。
3.2 关键参数与负荷的相互作用
本次试验采取先分别提高开环增益KA+-50%,以及+100%;减小励磁机时间常数TE+-50%,以及-80%。观察此发电机38的功角在负荷变动时不确定度变化情况。
故障对系统冲击的大小由第一摆幅值的大小所反映。第一摆幅值的大小也直接影响暂态稳定的传输功率以及极限系统的稳定。经过计算,如上表所示,在(200,200+50%)的取值范围内,KA的增大会一定程度上提高暂态稳定性(发电机功角第一摆期望的最大、最小值之差变小,意味第一摆幅值减小),但当KA进一步增大到+100%时,第一摆的幅值反而增大;而降低KA至原来的50%时,第一摆的幅值与原数据+50%时相比,第一摆的幅值一样减小,即±50%的数据变动起到了差不多的降幅效果,而+100%的数据反而降低了这一效果。
观察变化TE时暂态过程中发电机38的功角不确定性的影响情况,可以发现在(0.25 -80% ,0.25)这个区间内,随着TE减小,第一摆幅值减小,暂态稳定性在一定程度上有所提高。但当TE增大50%的时候,同样出现了幅值的减小,暂态性能的改善。
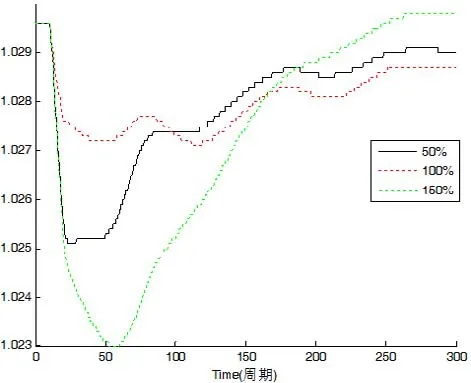
图6 TE摄动情况

表2 KA变动引起的功角不确定度

表3 TE变动引起的功角不确定度
4 结论
开环增益越大,从而强励倍数利用越充分,进而可以提高暂态稳定性的作法,前提是对应一个具体系统,KA取值在一个合适范围内,否则单一的提高开环增益,反而可能会对系统的暂态稳定起到副作用。于此同时,观察yDmax最大方差,Dmaxpn±标准差最大值可以发现,在原数据上的任何方向的变动,都无一例外的增大了功角的不确定度,因此可以看出,给定的这一组原始的EA励磁参数值,虽然不能保证是使系统暂态稳定性达到最佳的值,但却使负荷模型的变动引起的节点暂态稳定性的不确定度达到了最低值。
增大或减小励磁机时间常数TE以减慢或提高励磁系统响应速度,进而改善系统暂态性能这一说法,必须基于TE在一个合适的取值范围内,否则,可能会得出与之相反的结论。同时,yDmax最大方差,Dmaxpn±标准差最大值的情况也进一步说明了类似KA的情况,即TE取得一个合适的整定值,将有效降低负荷模型的变动引起的节点暂态稳定性的不确定度。
本刊保留所有文字、图表版权,未经许可不得转载、摘编。
编辑邮箱:emiunited@163.com

