基于双层柱状结构的声场局域与聚焦现象
韩建宁, 唐 帅, 杨 鹏
(1. 中北大学 信息与通信工程学院, 山西 太原 030051; 2. 中北大学 信息商务学院, 山西 晋中 030054)
基于双层柱状结构的声场局域与聚焦现象
韩建宁1, 唐 帅1, 杨 鹏2
(1. 中北大学 信息与通信工程学院, 山西 太原 030051; 2. 中北大学 信息商务学院, 山西 晋中 030054)
本文研究了浸没在水中双层柱状结构的声聚焦效应及声场奇异局域效应, 并探索了声聚焦频率与圆柱结构参数之间的关系. 研究表明:当超声波源入射到双层柱状结构表面时, 在圆柱结构中心会出现声聚焦效应, 并在不同频率下出现单极、 偶极及多极局域声场的高低周期分布, 且周围环境的声场声压几乎为零. 这种声聚焦效应源于干涉衍射以及金属圆柱结构中的位移本征模式.
声聚焦; 本征模式; 周期分布; 声场局域效应
0 引 言
由于声学超材料的特殊物理性质和其对声波传输方向的可操控性, 使得其被应用于越来越多的工程领域, 如军工领域、 生物医学领域、 通信工程、 水声探测等各方面已经取得了巨大技术突破[1-6], 声学超材料作为超材料的一个分支, 与光子晶体、 超磁性材料等一起, 有可能带来新的技术革命[7-10].
近年来, 声场局域可以通过多种方式来实现且完全异于声聚焦[11-15]. 一般通过声子晶体的负折射机制来实现, 如研究声子晶体的晶格以及栅格对聚焦的影响; 比较成熟的有通过声学超材料的设计对局域声场的实现, 如Gao Halo等人分别通过对声波一维相位以及三维相位的调控实现了声场的局域聚焦, Xia J P等人[16-20]利用气凝胶结构和金属圆柱实现了声场在结构中心的单极和多极局域现象, 即利用特殊的声学结构进行设计来实现声场的局域, Sun H等人通过类似的结构在空气中实现了高频单极声聚焦[21-26].
本文采用柱状结构, 并且在模型外围又加了一层呈环状周期性排列的柱状结构, 同时在模型的周围还对称增加了四个同样的点激励. 这样, 不仅可以实现声场的局域效应, 还有很强的聚焦效果.
1 模型设计
如图 1(a) 所示, 同样尺寸的细柱状结构黄铜在水中呈环状排列, 内部则是一块空心铜柱体, 共同构成声场局域聚焦模型. 如图 1(b) 所示, 入射线激励源对称分布于模型的上下左右四侧. 图1(b) 中r1和r2分别为内部空心铜柱的内径和外径,r1=13 mm,r2=15 mm, 外部圆环的半径r3=22.5 mm,小铜柱的直径d=3 mm. 此外, 外环铜柱两个相邻细柱间的角度均为9°.

图 1 声场局域模型在各角度的视图Fig.1 View of local sound field model at different angles
运用COMSOL Multiphysics软件的有限元法进行数值模拟, 通过改变频率, 得到了不同频率下的声场局域效应. 材料的目标参数如下: 黄铜的密度ρb=8 400 kg/m3, 声速Cb=4 400 m/s; 水的密度ρw=998 kg/m3, 声速Cw=1 483 m/s(温度296 K); 在空气中, 大气压强为100 Pa,ρw=1.21 kg/m3,Cw=344 m/s.
2 模型理论
首先计算入射平面声源激发黄铜圆柱产生的声压幅值分布, 平面声源对称分布于模型的四侧, 在平面声波入射时, 柱形结构之间的缝隙可以等效为任意一个次级振动波源, 任意波源发出的次级子波的相位不同, 且由平面声波波源到各个次级子波的距离所决定.
声波波动方程为

本文仅讨论频域, 时域可选取平衡后的任意时刻, 故可忽略时间因子e-iω t项. 取模型中心为原点, 建立极坐标系(ρ,φ), 平面波源距离模型的距离均为L0, 由几何关系可得, 当声源发出的平面波到达外侧环形结构时次级波源的相位为
设外环各个次级子波源的坐标为(R2,φn)(φn+1-φn=9°), 第n个子波源与两环之间内任意一点(ρx,φx)的声程差为

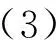
故(ρx,φx)处声波振幅干涉叠加后的大小为

由于内部铜柱对外环声波有一调制因子m作用S, 以影响中心声压的强弱, 因此在(ρx,φx)处声压的大小为

由式(5)即可计算外圈圆柱和内部圆环之间声场任意一点的局域声压大小, 但为近似计算的结果, 将来自于某一次级波源附近其他次级声场散射的二级小量的影响以调制因子m进行简化, 从而得到了比较合理的结果.
这样, 当叠加后的声波激发黄铜圆柱结构时, 由于任意方向的入射声源都可以在圆柱结构中产生声聚焦效应, 从而声源在圆柱中心聚焦成一个完美的圆形焦点. 在入射平面声源的作用下, 金属圆柱结构中一种位移本征模式被激发, 位移的振动方向沿着圆柱结构的径向. 因此, 在位移本征模式作用下, 入射声源的传播方向在圆柱内部发生重建, 传播方向均沿着圆柱的径向指向圆心, 最终在圆柱结构的中心聚焦.
3 模型的结果和讨论
3.1 模型的研究环境
声场的局域效应在不同的介质中有着不同的研究方向以及应用背景. 在不同的介质中有着不同的实现方案和实验结果. 由于与环境噪声消除、 深海潜艇信号检测, 以及科研前沿的密切联系, 声波在水和空气两种媒质的传播特性以及作用机理受到特别的关注与深入研究.
本文利用金属圆柱实现了水中声场在圆环中心单极和偶极以及多极的中心聚焦现象, 其实质是对特殊的声学结构进行设计, 进而实现声场的局域现象. 当声波透过模型后使得声场局域现象能够在水中实现, 而且, 本文在不同的频率下, 实现了声场在水中不同区域的周期性局域聚焦现象.
3.2 模型产生的多极声场局域效应
在自由空间中, 柱面声源声压幅值在传播方向上会迅速衰减. 然而在柱面声源激发模型时, 如图 2 所示, 在不同频率下, 柱面声源在空心圆柱中心产生了偶极、 四极、 六极、 八极、 十极和十二极等多极声场局域聚焦现象. 同时, 本文发现局域声场聚焦中心的极点个数与入射声波频率是呈正相关的, 如图 3 所示, 入射声波频率越大, 焦点个数也随之增多.
当入射声波进入模型外部柱状结构时, 会激发环状结构的共振模式, 使入射柱面声源的传播方向发生变化, 多焦点的声聚焦现象正是由环状结构不同的共振模式产生的. 当改变入射声波的频率为98.60 kHz时, 产生了偶极声场局域现象, 见图2(a), 即在99.60 kHz下中心声场产生偶极局域现象, 传播的声波限制于两个极点; 调制入射波的频率至124.70 kHz时, 产生了四极声场局域现象, 见图2(b), 即当频率升高, 局域现象出现多极化, 产生了四个固定极点, 中心呈对称分布; 在相对四极声场局域现象的基础上, 再次增大频率至148.17 kHz时, 出现六极声场局域, 六极分为三高三低, 其中三极声压较高, 另外三极声压较低, 中心交错分布, 见图2(c); 当平面波的频率171.40 KHz时, 产生了八极声场局域现象, 见图2(d). 此频率较前面的三个频率有所提高, 且呈现出更为奇特的四高, 四低的八极声场局域现象, 有八个呈对称分布的局域极点周期分布; 继续增大频率还可以看到类似的十级以及十二极等声场局域现象.

图 2 不同频率声波激励的声场分布图Fig.2 Sound field distributions of different frequencyincident acoustic stimuli
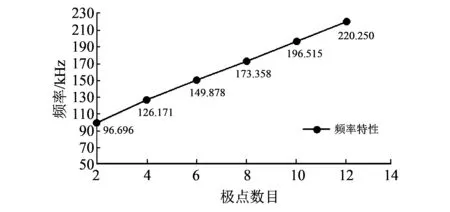
图 3 入射声源频率和极数之间的曲线关系Fig.3 The curve relation between the incident source frequency and the number of poles
以六极声场局域现象为例, 本文做出了柱面声波在自由空间传输时的相位图和在148.17 kHz产生六极声场局域现象时的相位图, 如图 4所示, 以此了解声波相位的传输特性. 由图4(a)可以看出, 在自由空间中相位波形几乎不受干扰, 由图4(b)可以看出, 有声场局域模型存在时, 在环状结构的共振模式下, 模型对相位有明显的调控作用. 此外, 由于水的密度较大, 在声波传输过程中对模型各个圆柱有应力的作用, 即考虑流固耦合边界效应情况下, 为更好地了解模型与介质, 以及各个小圆柱直接相互影响以及耦合作用机理, 同样以六极子为例, 做出模型的位移场图和应力示意如图4(c)所示, 可见在六极子局域情况时, 介质对外部圆环的作用应力不大, 而对内部空心铜柱的作用应力较大,且位移场较大,即流固耦合对空心铜柱的影响较大.
图 4 入射声源为148.17 kHz的声压相位分布和结构位移形变图Fig.4 Phase distribution of sound pressure and displacement deformation diagram of incident sound source at 148.17 kHz
此外, 为了探究外围铜柱环的层数对局域现象的影响, 本文以该模型为基础, 发现在模型外围再添加一层金属圆环, 实现相同局域效果所需要的频率变化不大, 本文以偶极、 四极以及六极声场局域现象为例, 如图5(a)~(c)所示, 在三层结构下, 产生偶极、 四极以及六极声场局域现象所需要的频率分别为98.2, 125.2和148.7 kHz, 与双层结构相比, 变化并不大, 因此模型外围只需加一层铜柱即可达到相对较好的局域效果.

图 5 三层结构的声场局域现象Fig.5 The sound field localization of the three layer structure
3.3 模型产生的单点聚焦效应
本文发现改变声源入射频率, 不仅可以实现多极声场局域效应, 而且可以实现声场的单点聚焦效果. 当存在模型且入射波频率为73.55 kHz时, 模型中心产生了较强的单极声场聚焦现象, 如图6(a)所示. 随着入射平面声波频率的不断增大, 产生了更为奇特的中心聚焦现象. 当频率为130.34, 187.8, 247.37 kHz时, 如图6(b)~(d)所示, 声波仍然聚焦于模型中心, 与图7(a)不同的是, 中心聚焦点随着频率的增大而越来越小, 同时中心焦点的声压幅值也随之越来越大, 如图7(a)~(d) 所示, 根据线图可以明显看出焦点的递减趋势与声压幅值的递增趋势. 此外, 聚焦频率呈线性增加, 且两个相邻聚焦频率间隔基本相同.

图 6 不同频率激励的中心聚焦声场分布图Fig.6 The focus distribution of the sound field with different frequencies

图 7 声压幅值分布线图Fig.7 Line diagram of pressure amplitude distribution
如图 8 所示, 与多极效应产生机理类似, 柱面波源在自由空间中的相位波形是一系列不受干扰的圆弧线, 而在外层环状结构的共振与内部空心铜柱的本征振动下, 柱面声源的相位波形在模型内部重建为一系列同心圆, 且每个圆上的相位值相等, 最终在圆柱中心形成一个圆形焦点.

图 8 入射频率为73.55 kHz柱面声源声场分布对比图Fig.8 Excitation of cylindrical sound source with incident frequency of 73.55 kHz
3.4 模型深度讨论
为了使本文的模型得到更广泛的应用, 探究了模型结构与频率的关系, 当改变模型内部空心铜柱尺寸时, 可以发现, 当空心铜柱尺寸变大时, 产生相同局域效果所需要的频率则会减小, 即产生同样声场局域现象所需要的频率与模型的尺寸是负相关的, 如图 9 所示.

图 9 入射声源频率与结构尺寸变换下的声场分布图Fig.9 The distribution of sound field between incident acoustic frequency and structural dimension change
3.5 模型应用环境的推广

图 10 空气中超材料局域声场分布图Fig.10 Local metamaterial sound field distribution in air
4 应 用
在诸如医学中的超声治疗或水下声学通讯等重要场合中, 声波能量必须通过聚焦、 偏折等手段来形成特定的声波波前以实现准确高效的诊断、 治疗或通信. 通过利用特殊构造的人工微结构来产生自然材料无法提供的反常相位或声折射率分布等, 可突破经典理论的限制, 为波阵面的操控提供全新的思路, 并产生传统意义上无法实现的特殊声学现象. 这将为声学器件的设计与制备提供启示, 对声学的各种应用乃至整个声学领域具有深远意义.
同时, 近十几年来, 人们对利用超声空化效应降解有机物的研究非常重视, 超声空化装置产生的能量集中、 空化效应强烈, 对各类有机物有良好的氧化效果, 但空化效应只在超声探头附近产生, 能量利用率较低, 难以对污水进行大规模处理, 本文的研究可以有效解决此类问题, 将能量有效地在水中进行单点或者多点聚焦, 从而极大地提高能量的利用率.
5 结 论
本文研究了声学材料的特殊结构在水中的声场局域效应和聚焦现象. 主要得出以下结论: 在本文的模型下, 实现了声波在水中的高低压周期性多极局域效应, 使局域现象的结果趋于低频化、 多极化. 在中心圆环内部, 实现了声波在水中的单点聚焦效应, 发现产生焦点的大小与频率是呈负相关的. 除此之外, 发现在模型中心产生的多极局域现象的极数与声波的频率是呈正相关的. 与此同时, 该模型在空气等其他介质中加以推广, 同样可以产生相同的声场局域效应, 使该模型的应用更为广泛.
[1] Zigoneanu L, Popa B I, Cummer S A. Design and measurements of a broadband two-dimensional acoustic lens[J]. Physical Review B, 2011, 84(2): 3214-3219.
[2] Li Y, Liang B, Tao X, et al. Acoustic focusing by coiling up space[J]. Applied Physics Letters, 2012, 101(23): 036609.
[3] Liu Z, Chan C T, Sheng P. Analytic model of phononic crystals with local resonances[J]. Physical Review B, 2005, 71(1): 014103(1-8).
[4] Wang W, Xie Y, Konneker A, et al. Design and demonstration of broadband thin planar diffractive acoustic lenses[J]. Applied Physics Letters, 2014, 105(10): 101904-101904-3.
[5] Gantzounis G, Serra-Garcia M, Homma K, et al. Granular metamaterials for vibration mitigation[J]. Journal of Applied Physics, 2013, 114(9): 12-41.
[6] Tian Y, Wei Q, Cheng Y, et al. Broadband manipulation of acoustic wavefronts by pentamode metasurface[J]. Applied Physics Letters, 2015, 107(22): 333-113.
[7] Zhang S, Yin L, Fang N. Focusing ultrasound with an acoustic metamaterial network.[J]. Physical Review Letters, 2009, 102(19): 194301.
[8] Jahdali R A, Wu Y. High transmission acoustic focusing by impedance-matched acoustic meta-surfaces[J]. Applied Physics Letters, 2016, 108(3): 82-149.
[9] Wang G, Yu D, Wen J, et al. One-dimensional phononic crystals with locally resonant structures[J]. Physics Letters A, 2004, 327(5): 512-521.
[10] Ke D, Ding Y, He Z, et al. Graded negative index lens with designable focal length by phononic crystal[J]. Journal of Physics D Applied Physics, 2009, 42(18): 185505-185508(4).
[11] Climente A, Torrent D, Sánchezdehesa J. Sound focusing by gradient index sonic lenses[J]. Applied Physics Letters, 2010, 97(10): 5325.
[12] Martin T P, Nicholas M, Orris G J, et al. Sonic gradient index lens for aqueous applications[J]. Applied Physics Letters, 2010, 97(11): 023902.
[13] Peng S, He Z, Jia H, et al. Acoustic far-field focusing effect for two-dimensional graded negative refractive-index sonic crystals[J]. Applied Physics Letters, 2010, 96(26): 1035.
[14] Martin T P, Layman C N, Moore K M, et al. Elastic shells with high-contrast material properties as acoustic metamaterial components[J]. Physical Review B Condensed Matter, 2012, 85(16): 1279-1284.
[15] Torrent D, Sánchezdehesa J. Acoustic metamaterials for new two-dimensional sonic devices[J]. New Journal of Physics, 2007, 9(9): 323.
[16] Lu J, Qiu C, Ke M, et al. Valley Vortex States in Sonic Crystals.[J]. Physical Review Letters, 2016, 116(9): 093901.
[17] Gao H, Gu Z, Liang B, et al. Acoustic focusing by symmetrical self-bending beams with phase modulations[J]. Applied Physics Letters, 2016, 108(7): 055002.
[18] Xia J P, Sun H X. Acoustic focusing by metal circular ring structure[J]. Applied Physics Letters, 2015, 106(6): 341.
[19] Sun H X, Zhang S Y, Yuan S Q, et al. Laser-generated lamb waves propagation in multilayered plates composed of viscoelastic fiber-reinforced composite materials[J]. International Journal of Thermophysics, 2016, 37(7): 68.
[20] Wang P, Lu L, Bertoldi K. Topological phononic crystals with one-way elastic edge waves[J]. Physical Review Letters, 2015, 115(10): 104302.
[21] Zhao J, Bonello B, Becerra L, et al. Focusing of rayleigh waves with gradient-index phononic crystals[J]. Applied Physics Letters, 2016, 108(22): 2022.
[22] Sun S H, Liu X L, Liu Z Y, et al. The angular distribution of optical emission spectroscopy from a femtosecond laser filament in air[J]. Chin.phys.lett, 2013, 30(4): 45202-045202.
[23] Sun H, Zhang S, Shui X. A tunable acoustic diode made by a metal plate with periodical structure[J]. Applied Physics Letters, 2012, 100(10): 104301.
[24] Sun H, Zhang S. Enhancement of asymmetric acoustic transmission[J]. Applied Physics Letters, 2013, 102(11): 013904.
[25] Chen L, Sun H X, Yuan S Q, et al. Broadband acoustic focusing effect based on temperature gradient distribution[J]. Acta Physica Sinica, 2016.
[26] Lu J, Qiu C, Ke M, et al. Directional excitation of the designer surface acoustic waves[J]. Applied Physics Letters, 2015, 106(20): 42.
LocalandFocusingofSoundFieldBasedonDoubleLayerCylindricalStructure
HAN Jian-ning1, TANG Shuai1, YANG Peng2
(1. College of Information and Communication Engineering, North University of China, Taiyuan 030051, China;2. College of Information and Business, North University of China, Jinzhong 030054, China)
The acoustic focusing effect and the singular local effect of the bilayer columnar structure immersed in water were studied, and the relationship between the acoustic focusing frequency and the cylindrical structure parameters was explored. The results show that when the ultrasonic source is incident on the surface of the double columnar structure, the acoustic focusing effect occurs in the center of the cylindrical structure. The high and low cycle distributions of single-stage, dipole and multi-stage local sound fields occur at different frequencies, and the sound pressure in the surrounding environment is almost zero. This acoustic focusing effect results from the interference diffraction and the displacement eigenmode in the metal cylindrical structure.
sound focus; intrinsic mode; periodic distribution; local effect of sound field
1673-3193(2017)05-0619-07
2017-06-12
国家自然科学基金资助项目(61671414)); 山西省青年基金资助项目(201601D202035)
韩建宁(1980-), 男, 副教授, 博士, 主要从事声学超材料设计的研究.
O426.5
A
10.3969/j.issn.1673-3193.2017.05.020

