基于特征点匹配对平面相似度的图像拼接

周 雪，曹 爽，何香静，邹见效



基于特征点匹配对平面相似度的图像拼接

周 雪，曹 爽，何香静，邹见效

(电子科技大学自动化工程学院 成都 611731)

针对来自于不同视点拍摄的具有视差的两幅图像，提出了一种基于特征点匹配对平面相似性的图像拼接方法。该方法利用场景中属于同一平面特征点之间的变换矩阵一致性的特点，通过定义特征点匹配对之间的平面相似度来筛选特征点匹配对，有效降低了特征点的漏匹配率，提高了配准精度。采用图割算法计算图像的最优缝合线，进行拼接得到最终结果。实验结果表明，与现有经典算法相比，该方法具有较好的视差鲁棒性。

特征点; 图割; 图像拼接; 平面相似度

图像拼接是将在相同场景下拍摄的存在一定重合部分的图像融合为一幅完整图像的方法[1]。对于广视角、宽视野的场景，使用普通相机已经难以满足需求，但是高档广角相机成本昂贵，而使用图像拼接技术则可以利用普通相机获取广视角图像，是计算机视觉、图像处理以及计算机图形学领域的研究热点之一。视频监控、医学、测绘、航空、航天等重要领域对先进图像拼接技术具有广泛而迫切的应用需求[2-3]。

基于特征点的图像拼接由于具有鲁棒性强、计算量小、运算速度快等优点成为现在图像拼接研究的主要方向和关注重点。该方法的核心是基于特征点的图像配准，具体来说是根据待拼接图像的特征点之间的匹配关系建立图像之间的变换模型，其主要步骤包括特征提取、特征匹配、坐标变换3个部分[4]。

文献[5]提出了具有尺度旋转仿射不变性的局部特征描述符(scale-invariant feature transform, SIFT)。文献[6]基于SIFT提出了SURF(speeded up robust features)特征检测算法，使用积分图和Haar小波降低计算量，使计算效率和特征描述子维度大大降低。文献[7]提出了一种FAST(features from accelerated segment test)角点检测算法。上述方法存在的不足在于，当待拼接图像中存在一定视差时，可能出现物体错位、虚影等结果。针对这一不足，专家学者们也进行了研究。

文献[8]利用3D重构思想，提出一种可以应用于任何场景和任何相机运动图像拼接方法。文献[9]提出一种平滑变化的仿射变换拼接模型来处理视差。文献[10]基于平滑变化的仿射变换做出了改进，采用非局部均值(non-local means)滤波求解各点的偏移量。文献[11]提出了一种as-projective-as-possible变换方法。文献[12-13]提出采用混合对齐的方法，先用单应矩阵对图像进行预对齐，再用内容保留变换方法进行修正。对于有视差图像的拼接，基于3D重构的拼接方法复杂度较高且对视差鲁棒性较差，而基于局部变换的拼接方法对参数设置比较敏感。

图像配准的结果对图像拼接的效果有着决定性影响，基于特征点匹配的方法[14]传统上会通过基于单应矩阵的RANSAC(random sample consensus)方法对特征点匹配对进行建模并筛选，但是这一过程可能会错误地筛去部分正确的特征点匹配对，从而影响最终得到的图像变换模型。这种情况主要由于RANSAC算法一般只能用来计算单个模型，对于多个不同平面的场景，视角有差异的图像之间会存在视差，使处于不同平面的特征点匹配对各自对应不同的模型，可能会筛去部分正确的特征点匹配对。即使通过循环多次使用RANSAC的方法，也容易使其遭遇随机初始点选取不恰当、内部迭代次数参数的选择等情况而导致求解不稳定、计算效率不高等问题。

因此，对于具有视差的拼接图像，本文提出了基于特征点匹配对平面相似度的拼接方法。通过来自于不同图像的匹配对信息定义彼此之间的平面相似度，根据平面相似度筛选出属于不同平面的特征点匹配对。本文方法有效地降低了特征点匹配对筛选的漏检率，规避了随机性选取样本导致计算结果偏差的风险，同时也避免了需要提高内部迭代次数才能获得较好的结果。

1 基于特征点平面相似度的图像拼接

1.1 方法概述

本文采用传统的基于图像配准和图像融合的框架拼接两幅具有重合区域的图像。首先利用基于SURF的特征点检测方法获取图像的特征点；其次，采用匹配算法获得待拼接图像之间的特征点匹配对，基于特征点匹配对信息计算彼此之间的平面相似度，再基于平面相似度的概念对处于空间中不同平面的特征点匹配对进行筛选；最后根据筛选后的匹配对进行图像配准，基于配准结构，再采用graph-cut方法寻找重合区域的最优缝合线，进行融合后完成图像拼接。

1.2 特征点匹配对平面相似度的定义

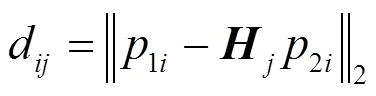
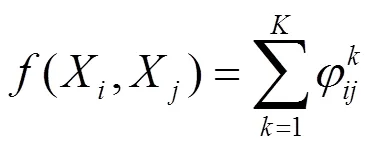
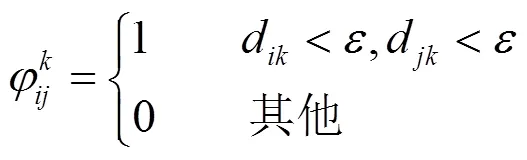
一般地，在图像中位于相同平面的特征点匹配对应该符合相同的单应矩阵，而异面的特征点匹配对往往不会符合同一单应矩阵。基于上述考虑，本文提出特征点匹配对平面相似度的概念。特征点匹配对的平面相似度反映了不同匹配对所属平面的接近程度，平面相似度越大，两个特征点匹配对所对应的平面就越接近。

1.3 基于平面相似度约束的特征点匹配对筛选算法

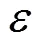
对本文使用的随机策略以及相关参数的选取进行说明。

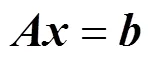
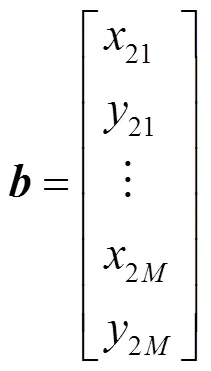
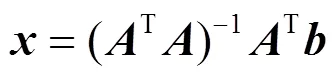
1.4 基于Graph-Cut算法的图像融合

对于两幅待拼接图像，可以使用上述得到的单应矩阵将其映射至空间中同一坐标系下，获取待拼接图像的重合部分。而图像融合方法则选取基于最优缝合线方法，主要目的是为了避免拼接后融合区域存在虚影、重影等现象。这种融合方法的思想是：重合区域中某个像素点，其值由两幅待拼接图像中的某一幅直接决定。这种思想决定了融合结果中不会有虚影、重影的现象产生。因此该方法实际上转化成在图像的重合部分找到一条线，满足在线两侧的图像之间总体上区分最小，而在这条线的两侧，分别使用不同的待拼接图像。通过对两幅图的重合区域建立图模型，采用基于Graph-cut的图分割算法对重合区域求解最优缝合线，具体算法参见文献[17]。基于计算所得最优缝合线，实现两幅待拼接图像的融合。

2 实验结果及分析

下面将本文方法对特征点筛选的性能进行验证，将其与目前广泛采用的基于单应矩阵的RANSAC算法进行对比。针对两幅待拼接图像，先进行SURF特征点提取与匹配，然后分别采用上述两种方法进行匹配对筛选，统计最终的匹配点对数目、误匹配对数目、误检率和漏检率。

实验参数配置如下：RANSAC的置信度设为0.995，算法的终止条件设为筛选出的特征点匹配对数量或剩余的特征点匹配对数量小于10。同时也进行了多次循环RANSAC的对比实验，单次RANSAC内迭代次数设置为2 000。在相同的硬件配置下：AMD Core 3.8 GHZ和8 GB RAM，本文方法耗时2.58 s，循环RANSAC耗时3.28 s。

本文测试了4组不同场景的图像，由于篇幅原因，只展示两组结果，更多定量比较结果如表1所示。

表1 不同图像组特征点匹配对筛选结果对比

实验对比结果如图1和图2所示。为了更好地对实验结果进行观察，在图1中使用不同灰度的线条分别连接初始特征点匹配对和使用RANSAC方法计算后的特征点匹配对，而对使用本文算法的计算结果，利用相同灰度的线条连接空间中共面的特征点匹配对。从图1的对比结果中，可以看出RANSAC算法的处理结果，对部分离镜头相对较远的正确特征点匹配对予以保留，去除了部分匹配不正确的特征点匹配对，但是也去除了一些离镜头相对较近的位于凉亭主体部位的正确特征点匹配对。对于这种情况，本文提出的方法在去除匹配不正确的特征点匹配对的基础上，对位于凉亭主体上的大部分正确匹配对予以保留。同时，使用循环RANSAC与本文方法进行对比，如图2所示。属于同一平面的特征点匹配对用同一种灰度进行标识。从对比结果可以发现，循环RANSAC(图2b)认为初始的特征点匹配对只分布在两个平面上就中止迭代了，而实际上可以观察到有大量的匹配对存在于地面、狮子、大门、墙面以及琉璃屋顶等不同的平面。基于本文提出的特征点匹配对筛选方法(图2c)大致将这些特征点匹配对划分在7个空间中不同平面上，这一结果相对更加符合实验图像所在的实际场景，有利于优化计算单应矩阵的准确度。

a. 使用SURF方法检测特征点和进行匹配所得匹配对

b. 使用RANSAC算法计算出的特征点匹配对

c. 使用本文算法计算出的特征点匹配对

由表1的4组实验结果定量对比分析可知，本文提出的特征点筛选算法，不但对绝大部分的匹配正确的特征点匹配对予以保留，而且去除了匹配错误的特征点匹配对，算法的漏检率相对RANSAC算法有了明显降低。

为了验证本文方法的有效性，将本文算法与APAP[11](as projective as possible image stitching with moving DLT)、Autostitch[12]拼接算法进行对比。其中Autostitch是根据文献[12]中提出的算法实现的拼接程序，经常被选择成为图像拼接算法的对比方法。考虑4种情况，对比实验结果分别如图3～图5所示，其中，图3a、图4a、图5a和图3b、图4b、图5b分别是两幅待拼接图像；图3c、图3d、图3e，图4c、图4d、图4e和图5c、图5d、图5e分别展示了上述3种方法的对比拼接结果和局部区域的放大图。

a. 使用SURF方法检测特征点和进行匹配所得匹配对

b. 使用循环RANSAC算法计算出空间中同面的特征点匹配对

c. 使用本文算法计算空间中同面的特征点匹配对

1) 楼房组：该图像组两个视点的图像尺寸均为1 000´662，图3为拼接结果。

a. 楼房组视点1图像

b. 楼房组视点2图像

c.Autostitch拼接结果

d. APAP算法拼接结果

e. 本文算法拼接结果

图3 楼房组拼接结果对比

a. 凉亭组视点1图像

b. 凉亭组视点2图像

c. Autostitch拼接结果

d. APAP算法拼接结果

e. 本文算法拼接结果

a. 船舶组视点1图像

b. 船舶组视点2图像

c. Autostitch拼接结果

d. APAP算法拼接结果

在图3中，两幅不同视点的图像拍摄于不同时间，视点1图像存在汽车，视点2图像中则没有汽车。可以在3种方法的拼接结果中发现，Autostitch方法的处理结果中出现了汽车的虚影，而APAP算法也出现了类似的问题，同时拼接的缝隙相对明显。使用本文方法的拼接结果，由于使用融合方法的特性，没有出现拼接虚影，拼接缝隙也得到了较好的处理，观察起来不明显。

2) 凉亭组：该图像组两个视点的图像尺寸均为1 000´662，图4为拼接结果。

在图4的拼接结果对比中，可以看出，Autostitch方法在处理凉亭的顶端和飞檐时出现了重影的情况。而APAP算法的处理结果中，凉亭顶部、凉亭飞檐、多根凉亭立柱均出现重影或明显弯曲。本文方法进行拼接后，在上述部位均未出现重影或弯曲，拼接效果相对较好。

3) 船舶组：该图像组两个视点的图像尺寸均为1 000´662，图5为拼接结果。

通过对图5的观察，可以发现，对于船舶组图像，Autostitch方法在处理近处的金属三角架以及远处的山体森林时有一定程度虚影产生。APAP算法的处理结果中，近处的金属架以及远处的吊车横臂都有重影现象存在。而使用本文方法进行拼接，融合区域没有出现物体错位或虚影，也没有出现明显的拼接缝，拼接结果相对上述两种方法更好。

3 结束语

本文提出了一种基于平面相似度的特征点匹配对筛选方法。对于具有视差的待拼接图像，根据处于场景中不同平面的特征点匹配对满足不同的变换矩阵的特性，提出了特征点匹配对平面相似度的概念，引入一种特征点匹配对筛选算法，将处于空间中同一平面的特征点筛选出来，降低了待拼接图像特征点之间的漏匹配率，改善了图像配准效果。并在上述基础上，设计了一种图像拼接方法，采集了若干组实验图像，对本文方法和几种现有图像拼接方法展开对比，实验结果表明本文提出的算法能够较好地对存在视差的图像进行拼接，对视差具有不错的鲁棒性。

[1] BRZESZCZ M, BRECKON T P. Real-time construction and visualisation of drift-free video mosaics from unconstrained camera motion[J]. Journal of Engineering, 2015, 1: 10.1049/joe. 2015. 0016.

[2] 郭一汉, 史美萍，吴涛. 基于GPU的实时图像拼接[J]. 计算机科学, 2012, 39(7): 257-261.

GUO Yi-han, SHI Mei-ping, WU Tao. Real time image mosaic based on GPU[J]. Computer Science, 2012, 39(7): 257-261.

[3] 王庆波. 基于DAS的实时全景视频拼接系统的设计与实现[D]. 成都: 电子科技大学, 2013.

WANG Qing-bo. Design and implementation of a real-time panoramtic videos stitching system based on DAS[D]. Chengdu: University of Electronic Science and Technology of China, 2013.

[4] 姜鹏飞. 基于ORB特征的视频图像拼接技术研究[D]. 成都: 电子科技大学, 2016.

JIANG Peng-fei. A reserach of videos stitching based on the ORB feature[D]. Chengdu: University of Electronic Science and Technology of China, 2016.

[5] LOWE D G. Object recognition from local scale-invariant features[C]//IEEE International Conference on Computer Vision. Corfu, Greece: IEEE Computer Society, 1999.

[6] BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer Vision and Image Understanding. 2008, 110(3): 346-359.

[7] ROSTEN E, PORTER R, DRUMMOND T. Faster and BETTER: a machine learning approach to corner detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(1): 105-119.

[8] DORNAIKA F, CHUNG R. Mosaicking images with parallax[J]. Signal Processing Image Communication, 2004, 19(8): 771-786.

[9] LIN W Y, LIU S, MATSUSHITA Y, et al. Smoothly varying affine stitching[C]//IEEE Conference on Computer Vision & Pattern Recognition. [S.l.]: IEEE Computer Society, 2011: 345-352.

[10] 苏昭, 王慈, 王涛. 一种具视差鲁棒性的图像拼接算法[J]. 电视技术, 2014, 38(15): 29-32.

SU Zhao, WANG Ci, WANG Tao. Robust anti-parallax imagestitching algorithm[J]. Video Engineering, 2014, 38(15): 29-32.

[11] ZARAGOZA J, CHIN T J, BROWN M S, et al. As-projective-as-possible image stitching with moving DLT[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2013, 36(7): 1285-1298.

[12] AGARWALAA. Content-preserving warps for 3D video stabilization[J]. Acm Transactions on Graphics, 2009, 28(3): 341-352

[13] ZHANG F, LIU F. Parallax-tolerant image stitching[C]// Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. [S.l.]: IEEE Computer Society, 2014: 3262-3269.

[14] 徐艳, 方二喜. 基于实时自动拼接技术的医学图像处理系统研究[J]. 电脑知识与技术, 2015, 11(27): 135, 138.

XU Yan, FANG Er-xi. A Research of medical image processing system based on the real-time automatic stitching technology[J]. Computer Knowledge and Technology, 2015, 11(27): 135, 138.

[15] BAY H, TUYTELAARS T, GOOL L V. SURF: Speeded up robust features[J]. Computer Vision & Image Understanding, 2006, 110(3): 404-417.

[16] SAMET H. The design and analysis of spatial data structures[M]. Reading, MA: Addison-Wesley, 1990.

[17] KWATRA V, SCHÖDL A, ESSAI, et al. Graphcut textures: Image and video synthesis using graph cuts[J]. ACM Transactions on Graphics, 2003, 22(3): 277-286.

编 辑 漆 蓉

Image Stitching Based on the Planar Similarity Among Matching Pairs of Feature Points

ZHOU Xue, CAO Shuang, HE Xiang-jing, and ZOU Jian-xiao

(School of Automation Engineering, University of Electronic Science and Technology of China Chengdu 611731)

An image stitching method for two images with parallax taking at different viewpoints is proposed based on the planar similarity among matching pairs of feature points. This method makes use of the property that feature points belonging to the same plane often share the same transformation matrix. By defining the planar similarity measure between feature point pairs, the missed matching rate is effectively decreased, and the image registration accuracy is improved. Subsequently, we adopt a graph cut-based algorithm to obtain the optimal stitching line. Experimental results on several datasets have demonstrated that our method outperforms the current state-of-art methods with a better anti-parallax robustness.

feature point; graph cut; image stitching; planar similarity

TP391.4

A

10.3969/j.issn.1001-0548.2017.05.015

2016-09-30；

2017-04-01

国家自然科学基金(61472063)

周雪(1981-)，女，博士，副教授，主要从事目标跟踪与检测方面的研究.