不等式恒成立(有解)问题的转换策略
江苏省常熟中学 (215500)
王 波
不等式恒成立(有解)问题的转换策略
江苏省常熟中学 (215500)
王 波
江苏省常熟中学参加了由苏锡常镇四市统一的高三第一次模拟考试,学校继续在苏州大市领跑,笔者特别关心数学一模的考试分析,通过对本班(物化班)和平行班的分析,得出了学校在难题上领先其他兄弟学校的结论,说明平时在中上等题上备课组所做的工作是充分的,特别是第19题导数问题,不等式恒成立(有解)问题一直是考试的重点和难点,主要有变量分离、函数性质和函数图像等几种办法,近几年不等式恒成立问题频频亮相于各地的高考及模拟题中,现通过例题的多种解法和大家一起探讨一下不等式恒成立(有解)问题的转换策略.
1.单变量的不等式恒成立(有解)问题
(2017苏锡常镇一模)已知函数f(x)=(x+1)lnx-ax+a(a为正实数,且为常数).
(1)若f(x)在(0,+∞)上单调递增,求a的取值范围;
(2)若不等式(x-1)f(x)≥0恒成立,求a的取值范围.
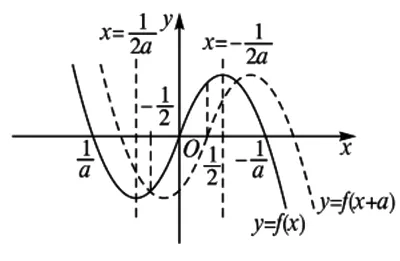
第(1)问略,第(2)问等价转换成当x>1时f(x)≥0,当0 (2)当0 综上所述,0 教学反思:这一道是用了分离变量和罗必塔法则来求解恒成立问题,在江苏高考中这一种解法是没有分数的,因为罗必塔法则是大学里的内容,超出了考试大纲的范围,在这一次苏锡常镇的一模考试中,如果用了这种方法,也是没有分数的,所有我们要对学生说明恒成立问题到最后需要用罗必塔法则的,要重新用另外的方法去做题. 解法2:(函数性质)第(2)问等价转换成当x>1时f(x)≥0;当0 x(1,x0)x0(x0,+∞)f′(x)-0+f(x)减极小值增 所以f(x) 当2 x(0,x0)x0(x0,1)f′(x)+0-f(x)增极大值减 所以f(x)>f(1)=0,当x∈(x0,1),矛盾. 综上所述,0 教学反思:以上解法是大部分同学做的一种方法,很多同学扣分的原因在于对于极值点存在性没有去证明,而且要证明唯一性,所以必须利用零点存在定理加单调性去证明,解题思路要严密,完美.当然还有一种非常类似的解法可以和大家分享. (1)当0 当0 (2)当2 x(1,x0)x0(x0,+∞)f(x)-0+f(x)减极小值增 所以当x∈(1,x0),f(x) 教学反思:解法3比解法2好,因为这样处理,零点可以直接求出,列表求单调性比较容易,函数的值域很容易可以看出,我们引导学生解题时,要比较这两种办法的优缺点,从而在今后的教学与测试中,对这类问题有非常深刻的认识,达到举一反三的效果.最后还有一种办法也是非常经典的. 解法4:(变形恒成立问题)第(2)问等价转换成当x>1时,f(x)≥0;当0 令ω(x)=x2+(2-2a)x+1,对称轴x=a-1,当a-1≤1,即0 x(1,x0)x0(x0,+∞)φ′(x)-0+φ(x)减极小值增 所以当x∈(1,x0),φ(x)<φ(1)=0,矛盾. (2)当0 当2 x(0,x0)x0(x0,1)φ′(x)+0-φ(x)增极大值减 所以当x∈(1,x0),φ(x)>φ(1)=0,矛盾. 综上所述,0 教学反思:这种方法中二次函数的零点存在问题不用去证明,由图像即知,相比较前几种方法,求导以后没有超越函数,分子是二次函数,很多同学利用根的分布很容易处理二次函数的正负问题,容易得到原函数的单调性,也避免了求二阶导数.所以在教学中,要引导学生打开思路,多去尝试各种方法,比较各种方法的优劣,利用最容易求导的函数去研究函数的单调性和值域问题,从而加深对导数的理解. (1)若函数f(x)在(1,+∞)上为减函数,求实数a的最小值; (2)若存在x1,x2∈[e,e2],使f(x1)≤f′(x2)+a成立,求实数a的取值范围. 命题“若∃x1,x2∈[e,e2],使f(x1)≤f′(x2)+a成立”等价于“当x∈[e,e2]时,有f(x)min≤ 教学反思:这种解法主要是先转化成一个变量的恒成立问题,再利用函数性质去解决恒成立问题,求函数的最小值时利用分类思想,可以说这题的分类讨论思想非常典型,可以把高中的知识融会贯通,给学生以醍醐灌顶的感觉,当然这道题还可以利用变量分离思想,简化解题步骤. 教学反思:通过分离变量,恒成立问题很容易求解,前提是变量分离以后函数的最值好求,如果最值要用罗必塔法则去求,那么这道题必须用函数性质去研究恒成立问题,在教学中,我们要用例题充分展示两种方法的优劣程度,进而提高学生的解题能力. 第一步:先把多变量问题分解成求每一个单变量问题的恒成立(有解)问题. 第二步:当对每一个变量做恒成立(有解)问题时,另一个变量看成是一个参数. 第三步:对每个变量研究恒成立(有解问题)时,我们可以用两种方法考虑,(1)变量分离法,一边是参数,另一边是变量,尽量分离成函数的最值容易求的形式.(2)函数性质法,研究带有参数的函数最值问题,尽量把函数转换成一阶导数,按照参数讨论函数的单调性.如果一阶导数研究问题困难,那么可以进行两阶求导,最终达到极值点好求,或者容易看出有极值点的情况,比如说二次函数,反比例函数,直线,三次函数等,如果不好求出极值点,对于复杂函数要利用零点存在定理,证明零点存在(即极值点是存在),再去列表,研究函数单调性和最值. 第四步:分清恒成立(有解)问题对应的函数最值,如果没有最值要仔细考虑等号是否取得的情况. 第五步:写出结论,检验合理性. (2017扬州市高三期末)已知函数f(x)=x(1+a|x|)(a<0),若f(x+a)≥f(x)对任意的x∈R恒成立,则实数a的取值范围是________. 图1 教学反思:图像法研究恒成立问题一般在填空题中会考察,要熟练掌握一些基本函数的图像与性质,大题中一般考察上面第三点的知识与步骤,需要课后多去反思及熟练应用,最终达到数学学习举一反三的能力. 含参不等式的恒成立(有解)问题越来越受到高考命题者的青睐,由于新课标高考对导数应用的加强,这些不等式的恒成立(有解)问题往往与导数问题交织在一起,这在近年的高考试题中不难看出这个基本的命题趋势.对含有参数的不等式,其破解方法主要有:分离参数法、函数性质法、数形结合法等. (1)分离参数法:分离参数法是解决含参问题的基本思想之一,对待含参的不等式问题在能够判断出参数的系数正负的情况下,可以根据不等式的性质将参数分离出来,得到一个一端是参数,另一端是变量表达式的不等式,只要研究变量表达式的性质就可以解决问题. (2)函数性质法:利用导数研究函数的性质,是处理含参问题的重要数学思想方法,通过求导,确定函数的单调性,极值,并结合零点性质确定参数的范围. (3)数形结合法:数形结合是一种重要的数学思想方法,其要点是“见数想形,以形助数”以达到解决问题的目的,数形结合是破解含参不等式恒成立问题的又一主要方法. 我们要重视方法的积累,高考复习千头万绪,只有夯实基础,总结解题思路,才能在考试中立于不败之地. [1]李敏.“罗必塔法则”在函数不等式恒成立中的应用[J].上海中学数学,2015(11):20-22. [2]郑一平.常规的分离参数解法为何半途而废[J].数学通讯,2014(4):12-13. [3]张惠.函数恒(能)成立的等价转换问题[J].福建中学数学,2017(3):4-5.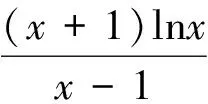

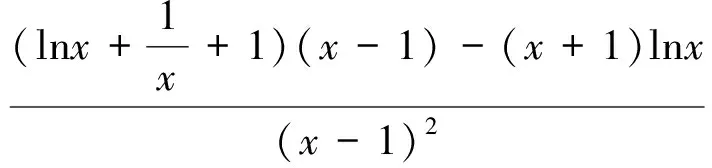
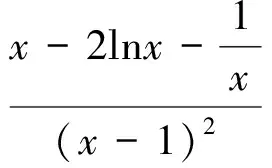
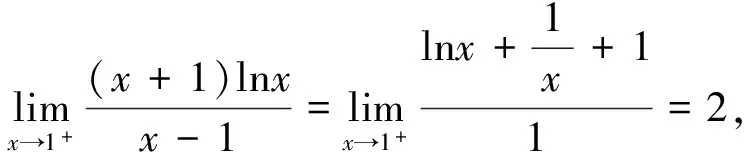
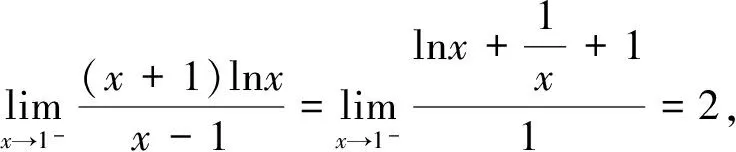
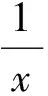


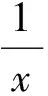

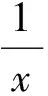

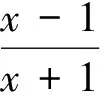
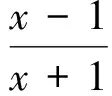



2.多变量的不等式恒成立(有解)问题

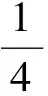
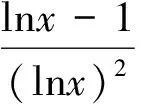
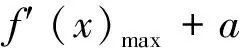
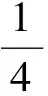
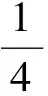
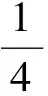
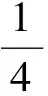
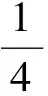
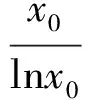

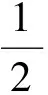
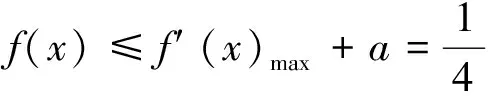
3.不等式恒成立(有解)问题的一般方法和主要思路
4.填空题中恒成立(有解)问题还可以通过图像解决
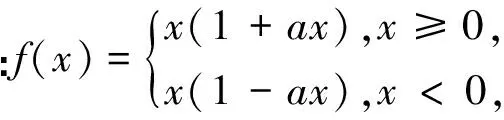
5.知识梳理,总结回顾

