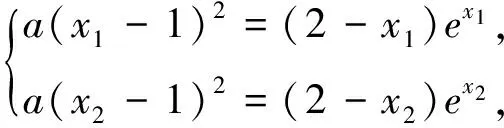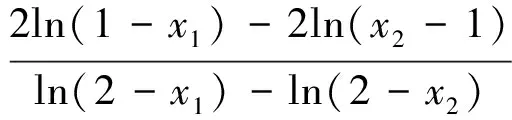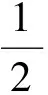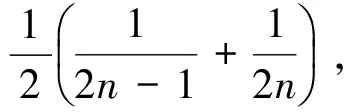巧用对数均值不等式解高考压轴题*

福建省泉州市第七中学 (362000)

彭耿铃

巧用对数均值不等式解高考压轴题*

福建省泉州市第七中学 (362000)

彭耿铃

研究高考试题、备战高考是师生的重要任务，而高考压轴题自然而然是最受关注的试题之一.

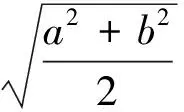
例1 (2016全国课标Ⅰ卷理科21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(Ⅰ)求a的取值范围；

(Ⅱ)设x1,x2是f(x)的两个零点,证明：x1+x2<2.

解析：(Ⅰ)略；(Ⅱ)由(Ⅰ)知a>0,x1<1

例2(2014年陕西理科卷21题)设函数f(x)=ln(1+x),g(x)=xf′(x)(x≥0)，其中f′(x)是f(x)的导函数.

(Ⅰ)g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N，求gn(x)的表达式；

(Ⅱ)若f(x)≥ag(x)恒成立，求实数a的取值范围；

(Ⅲ)设n∈N+，比较g(1)+g(2)+…+g(n)与n-f(n)的大小，并加以证明.

解析：(Ⅰ)、(Ⅱ)略.

例3 (2013年全国大纲卷22题)设函数

(Ⅰ)若x≥0，f(x)≤0，求λ的最小值；

例4 (2010天津理科21题)已知函数f(x)=xe-x(x∈R).

(Ⅰ)求函数f(x)的单调区间和极值；

(Ⅱ)已知函数y=g(x)的图像与函数y=f(x)的图像关于直线x=1对称，证明当x>1时，f(x)>g(x)；

(Ⅲ)如果x1≠x2，且f(x1)=f(x2)，证明x1+x2>2.

解析：(Ⅰ)、(Ⅱ)略；

x1+x2>2.

[1]林运来.对数学教师学科素养的几点思考[J].数学通讯.2016(2下半月).

[2]彭耿铃.对一道高考试题的再探究[J].数学通讯.2015(3上半月).

*本文为2016年度福建省教育科学“十三五”规划课题《基于全国课标Ⅰ卷函数与导数的考察研究》研究成果，课题编号：FJJKXB16-314.