基于MFCC与PCA的滚动轴承故障诊断*
王 前,于嘉成,宁永杰
(中国矿业大学 信息与控制工程学院,江苏 徐州 221116)
基于MFCC与PCA的滚动轴承故障诊断*
王 前,于嘉成,宁永杰
(中国矿业大学 信息与控制工程学院,江苏 徐州 221116)
针对振动传感器不易安装、传统分类算法训练时间较长等问题,提出了基于美尔倒谱系数(MFCC)与主成分分析(PCA)的滚动轴承故障诊断方法。首先利用声音传感器采集滚动轴承声音信号,而后提取声音信号的MFCC特征,最后将MFCC特征作为PCA分类器的输入进行故障分类,并与反向传播神经网络(BPNN)、支持向量机(SVM)进行比较研究。实验结果表明:MFCC系数可以有效反应轴承不同工作状态下的信号特征;基于MFCC与PCA的轴承故障诊断方法能够准确、有效地识别轴承故障类型。
轴承;故障诊断;美尔倒谱系数
0 引言
滚动轴承是旋转机械中的重要组件,它在旋转机械中起关键作用, 其工作状态正常与否直接影响整台机组的性能,因此,能否快速、精准地检测出轴承故障的存在和严重程度对于保障轴承安全可靠地运行和减少设备停机成本意义重大[1]。传统的振动信号故障诊断技术因为接触式测量、传感器不易安装等缺点,并不适用于某些特点场合,如高温、高腐蚀场合[2],因此,基于声音信号的故障诊断技术成为近几年比较新的课题[3]。MFCC特征因其提取简单、预测精度高、抗噪性能好等特点,已在语音识别领域获得了广泛应用[4]。因此,本文将MFCC参数用于轴承声音信号特征的提取。
现有的故障分类方法主要有神经网络(NN)[5]、支持向量机(SVM)[6]、隐马尔可夫模型(HNN)[7]、主成分分析(PCA)[8]、高斯混合模型(GMM)[9]等。其中,神经网络具有非线性映射能力强、无需建立复杂数学模型等优势[10],但存在训练时间过长,容易陷入局部最优解等问题;SVM具有唯一的全局最优解[11],但存在对大规模样本难以实施,解决多类问题存在困难等不足。PCA不仅是一种无监督降维工具,也可作为一种监督型分类算法[12],具有训练速度快、计算量小等优势。Chen Jing[13]等将PCA分类用于复杂工业过程故障诊断,并取得了不错的试验效果。故本文提出了基于MFCC与PCA的轴承故障诊断方法。并在此基础上,与反向传播神经网络(BPNN)、支持向量机(SVM) 进行对比研究。
1 MFCC特征的提取
Mel 倒谱系数(MFCC)将人耳的听觉感知特性和语音的产生机制相结合,经常被用在声音特性分析中[14],MFCC特征提取包括分帧、预处理、离散傅立叶变换、Mel带通滤波、离散余弦变换等步骤[15]。图1为MFCC特征提取流程。

图1 MFCC特征提取流程
物理频率与Mel频率之间的关系如式(1)所示。
Mel(f)=2595×lg(1+f/700)
(1)
算法具体步骤如下:
(1)对声音信号进行分帧,预处理(加窗、预加重),预处理的目的是为了补偿分帧所造成的信息损失,加窗时使用hamming窗。
(2)对预处理后的每帧信号作离散傅立叶变换(DFT)。设预处理后的时域信号为s(n),DFT变换后的频域信号S(k)可表示为下式:
(2)
(3)求S(k)的平方,得到能量谱,再使用M个Mel带通滤波器进行滤波,第m个滤波器的传递函数为:
(3)

(4)计算每个滤波器组的对数能量。第m个滤波器组的对数能量为:

(4)
(5)经离散余弦变换(DCT)即可得到Mel倒谱系数:
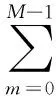
(5)
其中,M为Mel滤波器的个数,也是MFCC特征的维数。
2 基于PCA的分类算法
PCA是通过正交变换将数据空间映射到低维空间的数学方法,通过寻求一组正交基向量,使得原始数据被基向量分解后的信息损失最小,PCA分类的基本步骤如下[12]:
(1)设有m条训练样本s1,s2,s3,…,sm,每条样本的维度为n,将训练样本标准化,令训练样本集合的每一维特征均值为0,方差为1,得到标准化后的训练样本x1,x2,x3,…,xm;
(2)设X是由m个样本按行排列而成的样本矩阵,即X={x1},x2,x3,…,xm}T,计算其协方差矩阵:

(6)
(3)将协方差矩阵对角化,求得协方差矩阵的特征向量p1,p2,p3,…,pn,将特征向量按特征值的大小依次排列构成矩阵P,令式(7)成立。
S=PVPT
(7)
其中,对角矩阵V=diag(λ1,λ2,…,λn),λ1≥λ2≥…≥λn是协方差矩阵S的特征值。
(4)将测试样本标准化,设标准化后的样本为x,类数为k,按式(8)计算该样本针对每一类的判别评分g1,g2,…,gi,…,gk(i为类别标号),评分最高的类别即为该样本的输出类别j。
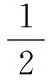
(8)
(9)

3 仿真研究
3.1 信号采集
为了验证本文所提方法的可行性,本文利用MFS-MG2010机械故障实验台模拟了四类轴承运行状态:正常、滚珠故障、内圈故障、外圈故障。通过声音传感器采集了四种状态下的声音信号。电机转速为1700rpm,录音采样率为44100Hz。四种模式下的声音信号如图2所示。

图2 轴承声音信号
3.2 特征提取
将所测信号每256个点分为一帧,每一类信号截取1500帧,共有6000帧数据。对每一帧做MFCC特征提取,特征维度设为24,形成6000个样本。每一类中随机抽取1000个样本用作训练样本,其余样本用作测试样本,图3为轴承外圈故障时1000组MFCC特征第3维、第4维的数据分布。

图3 第3维、第4维MFCC特征分布
3.3 故障分类
将6000个样本分为训练样本、测试样本,其中训练样本数量为4000个(每类各有1000个),测试样本数量为2000个(每类各有500个)。将训练样本标准化处理,使样本集每一属性的均值为0,方差为1;通过标准化后的训练样本训练PCA分类器模型,将测试样本标准化后输入PCA分类器进行故障分类,计算测试样本针对每一类故障的判别评分,评分最高的故障类别即为分类器输出类别。将2000个测试样本按照外圈故障、滚珠故障、内圈故障、正常的类别顺序排放,分类结果如图4所示。
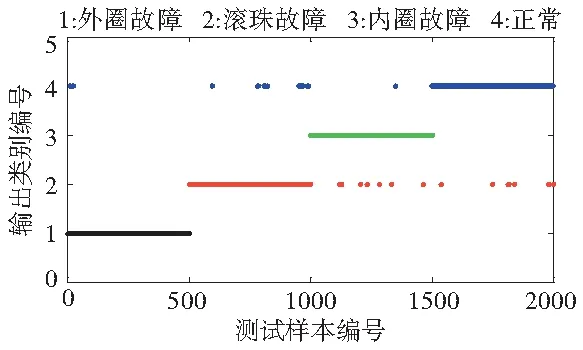
图4 分类结果
PCA分类算法的整体正确率为97.9%,训练用时为0.11s,对4种故障的测试结果见表1。

表1 四种故障测试结果
采用BPNN、SVM进行对比研究,比较三种分类算法的速度与正确率,BPNN采用三层神经网络结构,输入层单元数与特征维度相同为24,隐藏层单元数为20,输出层单元数为4;支持向量机采用LIBSVM工具包。三种算法的训练时间及准确度见表2。

表2 分类结果比较
实验结果表明,针对MFCC特征,三种算法都有着较高的准确度,但是BPNN、SVM训练时间较长,而PCA分类训练时间短于前两者,拥有计算量小、速度快的优势,因此更适合基于MFCC特征的轴承故障分类。
4 结束语
本文通过声音传感器获取了滚动轴承在正常、内圈故障、外圈故障、滚珠故障四种状态下的声音信号。采用MFCC系数作为特征参数,将PCA成功用于轴承故障识别,与BPNN、SVM的对比结果表明基于MFCC与PCA的轴承故障诊断模型训练速度更快,具有很强的可行性与实用性。
[1] Zhang Xiao-yuan, LiangYi-tao, Zhou Jian-zhong, et al.A novel bearing fault diagnosis model integrated permutation entropy ,ensemble empirical mode decomposition and optimized SVM [J] . Measurement,2015, 69: 164-179.
[2] 李宏亮,黄民,高宏,等.基于声信号的滚动轴承故障诊断[J].组合机床与自动化加工技术,2016(7):86-88.
[3] 周宴宇,杨胜跃,何正明,等.基于MFCC与LPCC的滚动轴承故障音频诊断法[J].微计算机信息,2009, 25(11-1):123-124.
[4] 王伟,邓辉文.基于MFCC参数和VQ的说话人识别系统[J]. 仪器仪表学报, 2006, 27(6) : 2253-2255.
[5] 王斌.基于小波分析和BP神经网络的滚动轴承故障诊断方法研究[D].兰州:兰州交通大学,2014.
[6] 何学文,赵海鸣.支持向量机及其在机械故障诊断中的应用[J].中南大学学报:自然科学版,2005,36(1):97-101.
[7] 吴军,邵新宇,邓超. 隐马尔科夫链模型在装备运行可靠性预测中的应用[J].中国机械工程,2010,21 ( 19 ) :2345-2349.
[8] H Abdi, L J Williams.Principal component analysis, Wiley Interdiscip[J].Comput.Stat,2010,2(4): 433-459.
[9] 李元,孙健. 基于高斯混合模型和变量重构组合法的故障诊断与分离[J].南京航空航天大学学报,2011,43(s):207-210.
[10] Hashemi Z,Mardaneh M,Sha Sadeghi M.High performance controller for interior permanent magnet synchronous motor drive using artificial intelligence methods[J].Scientia Iranica, 2012, 19(6):1788- 1793.
[11] 丁世飞,齐丙娟,谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报,2011,40(1):2-10.
[12] L H Chiang, R D Braatz, E L Russell.Fault Detection and Diagnosis in Industrial Systems[M]. German:Springer, 2001.
[13] Chen Jing, Jian Hou. SVM and PCA based fault classification approaches for complicated industrial process[J]. Neurocomputing , 2015 , 167:636-642.
[14] 王彪.一种改进的MFCC参数提取方法[J].计算机与数字工程,2012,40(4):19-21.
[15] 常飞,乔欣,张申,等.基于 MFCC 特征提取的故障预测与评价方法[J].计算机应用研究,2015,32(6):1716-1719.
FaultDiagnosisofRollingBearingBasedonMFCCandPCA
WANG Qian, YU Jia-cheng, NING Yong-jie
(School of Information and Electrical Engineering, China University of Mining and Technology, Xuzhou Jiangsu 221116,China)
Aimed at the problem that the vibration sensor is difficult to be installed and the conventional classification algorithms take a long time to be trained, this paper proposes a method of fault diagnosis for rolling bearing based on MFCC and PCA. Firstly, acoustic sensor is used to acquire acoustic signals of rolling bearing. Then, MFCC features are extracted from the signals. Finally, MFCC features are used as the inputs of PCA classifier for fault classification and its performance is compared with BPNN and SVM. The experimental result shows that MFCC can represent the features of rolling bearing in different conditions and the method based on MFCC and PCA can detect the fault category accurately and effectively.
bearing; fault diagnosis; MFCC
TH165+.3;TG506
A
1001-2265(2017)12-0103-03
10.13462/j.cnki.mmtamt.2017.12.025
2017-02-28
国家重点研发计划资助(2017YFC0804404)
王前(1991—),男,江苏徐州人,中国矿业大学硕士研究生,研究方向为机械故障诊断,(E-mail)wangqiancumt@126.com。
(编辑李秀敏)

