基于步长控制的铣削稳定性预测全离散法*
刘成颖,张 洁,刘 巍,张 智,3
(1.清华大学 机械工程系,北京 100084;2.精密超精密制造装备及控制北京市重点实验室,北京 100084;3.海军航空工程学院 飞行器工程系,山东 烟台 264001)
基于步长控制的铣削稳定性预测全离散法*
刘成颖1,2,张 洁1,2,刘 巍1,2,张 智1,2,3
(1.清华大学 机械工程系,北京 100084;2.精密超精密制造装备及控制北京市重点实验室,北京 100084;3.海军航空工程学院 飞行器工程系,山东 烟台 264001)
基于控制离散步长来保证预测精度的思想,提出了一种改进的用于预测铣削稳定性叶瓣图的时域全离散法。一直以来,铣削工艺系统的动力学过程被看作带有单个延时反馈量的周期性线性系统,其数学模型是无限维时滞微分方程组。全离散法在一个周期内将时滞微分方程离散为有限个常微分方程,求解前后两步的状态转移矩阵,继而得到一个完整周期内的状态转移矩阵。在选定的转速范围内循环求解过程中,通过控制离散步长小于设定值来达到提高低转速条件下全离散法的收敛率的目的。通过仿真和切削实验,证明方法具有较高的预测精度和计算效率。
铣削稳定性;Floquet理论;步长控制;收敛率
0 引言
铣削加工过程中的颤振是一种严重的系统失稳现象。颤振迫使工艺人员选取保守的切削参数,降低材料去除率,而且颤振会大大降低加工质量甚至使工件报废。再生理论较好地解释了颤振的机理并获得了大量的实验验证[1],该理论认为上一个刀齿切削时留下的表面波纹会影响当前刀齿的瞬时切削厚度,即切削时存在延时反馈,该反馈可能引起系统发散。工艺系统的动力学模型被归结为包含周期系数矩阵的时滞微分方程组,由于方程中存在时滞项,其单值算子和相空间均为无限维,因此不存在闭形解[2]。
对于该方程组的近似求解方法,可归纳为频域法和时域法两种。Altintas等将方程中的周期系数矩阵展开成傅立叶级数,只保留其平均量,得到了可在频域中解析计算稳定性边界的单频率法[3]。单频率法具有极高的计算效率,但在小径向切深时不能预测出附加不稳定区域。之后Altintas等考虑周期系数矩阵的前r阶级数,推广得到了多频率法解决了这一问题[4],但该方法计算效率较低,应用不多。Insperger等提出了半离散法[5],该方法在时域上将时滞项离散,利用插值法将时滞微分方程化简为一系列的常微分方程,首先获得相邻两步之间的状态转移矩阵,继而获得一个完整时滞周期上的状态转移矩阵,并应用Floquet定理判定铣削过程的稳定性。Ding等将状态项全部离散,基于直接积分格式推导得到了计算效率更高的全离散法[6]。时域离散方法兼顾了计算精度和计算效率。使用稳定性判断方法,扫描选定的工艺参数范围(通常是转速和切深),便可得到稳定性叶瓣图。稳定性叶瓣图直观地给出了工艺系统稳定区域和不稳定区域的边界,对于通过合理选取工艺参数来避免颤振并获得较大的材料去除率具有极大的指导意义。
在扫描转速区间时,模型的时滞项发生变化,在低转速条件下时滞项要大于高转速条件下的时滞项。虽然通过不同的插值方法和插值阶次,发展出了多种具有更低阶局部离散误差的离散方法[7-9],但通常的通过固定离散步数来进行稳定性判断的做法,可能存在低转速下收敛率过低的问题。通过设定初始时间步长来确定每个转速较为合理的离散步数,不仅可以提高低转速区间的收敛率,而且可以提高整个计算流程的计算效率。
1 动力学模型及全离散法判稳
不失一般性,考虑再生效应并略去切削力中的静态成分,刚性工件柔性刀具双自由度铣削工艺系统的动力学模型为:
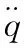
(1)
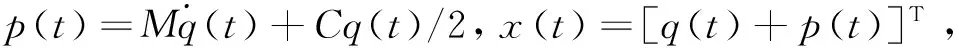
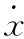
(2)
其中,
设定初始时间步长τ0,则一个刀齿切削周期等距离散为m步,且:
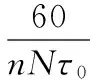
(3)
则实际时间步长τ=T/m。
其中,ceil(·)表示向上取整,以控制实际时间步长不大于设定值τ0,mlim是人工设定的最小离散步数,以避免时滞量较小时因离散步数过小而导致预测精度不足。离散时间点为:
tk=t1+(k-1)τ,k=1,2,…,m+1
在第k步和第k+1步之间,即kτ≤t≤(k+1)τ时,状态空间方程的解为:
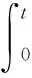
(4)
将周期项A(kt+t-x)和B(kt+t-x),状态项x(kτ+τ-ξ),时滞项x(kτ+τ-ξ-T)进行插值处理并积分可得xk+1的显式表达式:
xk+1=[I-Fk+1]-1(F0+F0,k)xk+[I-Fk+1]-1Fm-1xk+1-m+
[I-Fk+1]-1Fmxk-m
(5)
其中,
构造离散映射yk+1=Dkyk
(6)
其中,
yk=col(xkxk-1…xk+1-mxk-m)
(7)
(8)
可构造一个完整周期上的状态转移矩阵
φ=Dm-1Dm-2…D1D0
(9)
最后可应用Floquet定理判断系统的稳定性,即若转移矩阵的所有特征值的模均小于等于1,则系统稳定,否则系统发散。
2 叶瓣图仿真分析
为检验方法的精度和计算效率,选取文献中的双自由度算例进行叶瓣图仿真分析:
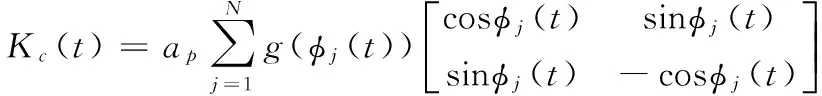
(10)
其中,φj(t)是第j个刀齿的角位置;g是用来判断刀齿切削状态的窗函数,当刀齿切削时g=1,刀齿退出切削时g=0;N是刀齿数目。刀具为两齿刀,刀具x和y方向的模态对称,模态质量mt=0.03993kg,阻尼比ζ=0.011,固有频率fn=922Hz;切削力系数分别为Kt=6×108N/m2和Kr=4×108N/m2。刀具浸入比为1,顺铣。
Insperger等[10]证明当离散步数m足够大时,时域离散法获取的稳定性界限将收敛到真实值。因此,应用1阶全离散法,取m=200绘制的叶瓣图作为真实参考值,用于对比仿真曲线的精度。所有仿真曲线的叶瓣图均将转速-切深二维平面划分为200×100的网格。仿真结果如图1所示,点划线表示准确的稳定性边界。结果表明,基于步长控制的方法在计算效率占优的情况下依然具有更快的收敛速率,尤其是在低转速即大时滞情况下对比更为明显。所有运算均基于MATLAB®2016a平台并在同一台电脑上(intel core(TM) i7-6700HQ, 2.6 GHz, 8 GB)完成。
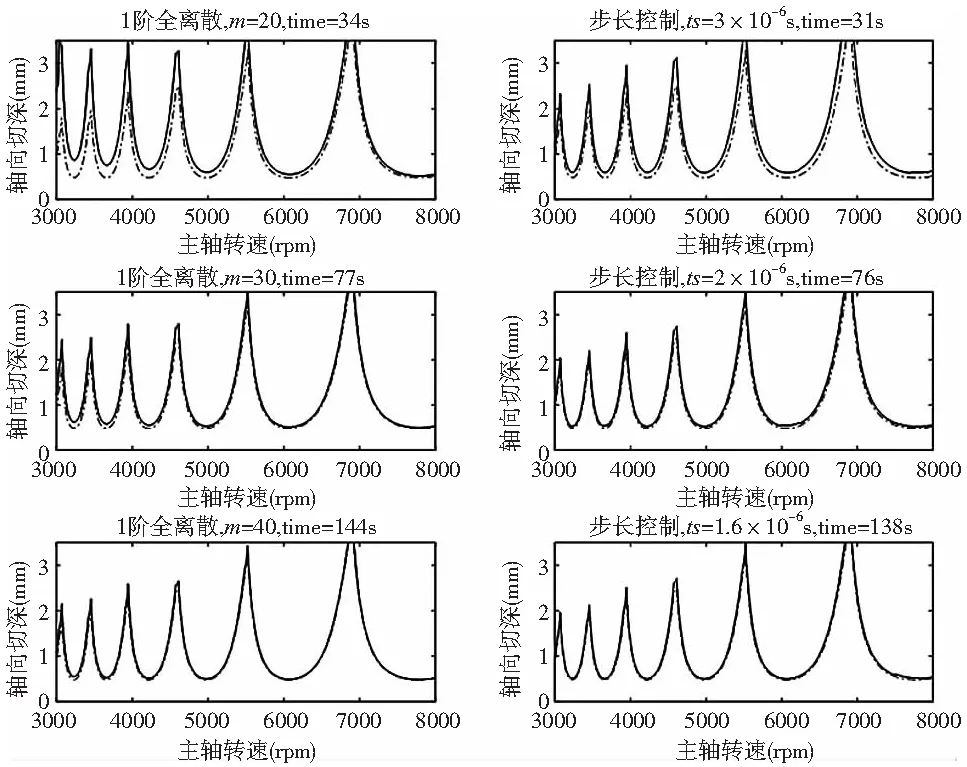
图1 1阶全离散法和控制步长全离散法仿真对比
3 实验验证
验证试验在VMP-23加工中心上展开,机床最高转速10000rpm。实验所使用的刀具为普通硬质合金两齿立铣刀,直径为12mm,安装长度60mm,工件材料是7075-T6航空铝合金。通过模态试验和切削力系数辨识实验获取的模态参数及切削力系数如表1所示。刀具浸入比为1,逆铣。

表1 实验刀具部分参数
使用步长控制方法得到的叶瓣图如图2所示,初始步长为1×10-6s。为验证方法的有效性和叶瓣图的准确性,在稳定区域和颤振区域选取不同的转速切深组合进行切削实验。实验过程中,使用Kistler 9257B测力仪和Kistler 5070A功率放大器来采集切削力,实验过程中均没有使用切削液。图中,圆圈代表稳定点,叉代表颤振点,圆圈和叉重叠代表不确定点。从实验结果来看,叶瓣图很好地预测出了工艺系统的稳定区域。

图2 实验刀具稳定性叶瓣图
选取叶瓣图中典型的稳定点和颤振点进行对比。图2中参数点A(7500rpm,0.5mm)和参数点B(8000rpm,0.5mm)的Y向切削力频谱分别如图3a和图3b所示。工艺系统在A点发生颤振,颤振频率为2172Hz,接近于系统固有频率,而在B点稳定,其频谱的峰值均为刀齿通过频率的分频和倍频。
4 结论
(1)通过步长控制,可避免在使用时域离散方法判定大时滞量时滞微分方程敛散性时因离散步数不足而导致的收敛率过低的问题,即可在保证计算效率的前提下提高叶瓣图计算过程中低转速区间的收敛率。
(2)稳定性叶瓣图可以准确预测工艺系统的稳定区域。在两个叶瓣之间存在稳定切深较大的稳定区域,通过合理选取稳定区间内的工艺参数,可以在稳定工况下获取较大的加工效率。
(3)在切削非薄壁件工况下,刀具往往是工艺系统最薄弱的环节,而不同的刀具以及相同刀具的不同安装方式均具有不同的稳定性叶瓣图。怎样快速获取稳定性叶瓣图以及如何通过合理选取刀具和安装方式来获取更优的稳定区域需要进一步的研究。
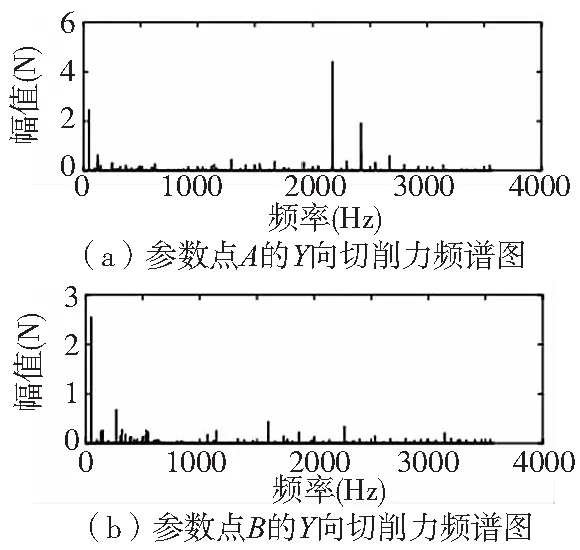
图3 稳定点与颤振点切削力频谱图
[1] Quintana G, Ciurana J. Chatter in machining processes: a review[J]. International Journal of Machine Tools and Manufacture, 2011, 51(5): 363-376.
[2] 丁汉, 丁烨, 朱利民. 铣削过程稳定性分析的时域法研究进展[J]. 科学通报, 2012, 57(31): 2922-2932.
[4] Merdol S D, Altintas Y. Multi Frequency Solution of Chatter Stability for Low Immersion Milling[J]. Journal of Manufacturing Science & Engineering, 2004, 126(3):459-466.
[5] Insperger T, Stépán G. Semi-discretization method for delayed systems[J]. International Journal for numerical methods in engineering, 2002, 55(5): 503-518.
[6] Ding Y, Zhu L M, Zhang X J, et al. A full-discretization method for prediction of milling stability[J]. International Journal of Machine Tools and Manufacture, 2010, 50(5): 502-509.
[7] Insperger T, Stépán G. Updated semi-discretization method for periodic delay-differential equations with discrete delay[J]. International Journal for Numerical Methods in Engineering, 2004, 61(1): 117-141.
[8] Ding Y, Zhu L M, Zhang X J, et al. Second-order full-discretization method for milling stability prediction[J]. International Journal of Machine Tools and Manufacture, 2010, 50(10): 926-932.
[9] Qiang Q, Sun Y, Jiang Y. On the accurate calculation of milling stability limits using third-order full-discretization method[J]. International Journal of Machine Tools & Manufacture, 2012, 62(1):61-66.
[10] Insperger T. Full-discretization and semi-discretization for milling stability prediction: Some comments[J]. International Journal of Machine Tools & Manufacture, 2010, 50(7):658-662.
AFull-discretizationMethodforMillingStabilityPredicationBasedonTime-stepControl
LIU Cheng-ying1,2, ZHANG Jie1,2, LIU Wei1,2, ZHANG Zhi1,2,3
(1. Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China;2. Beijing Key Lab of precision/Ultra-precision Manufacturing Equipment and Control, Beijing 100084, China)
A modified full-discretization method is proposed for milling stability prediction based on time-step control. The dynamic process of milling system is regarded as a linear periodic system with a single time delay and its mathematical model is formulated as delay-differential equations(DDEs). By dividing the delay period equally into a set of time steps, the state transition matrixes between the adjacent two steps could be deduced by the full-discretization method. Then the state transition matrix over one delay period is structured. By controlling the time steps not exceeding the set value when scanning the objective range of rotating speed, the full-discretization method converges faster than setting a constant time interval value. At last the modified method is verified by simulation and experiments.
milling stability; Floquet theory; time-step control; rate of convergence
TH161;TG506
A
1001-2265(2017)12-0059-03
10.13462/j.cnki.mmtamt.2017.12.014
20147-03-15
国家04科技重大专项课题(2013ZX04001-021)
刘成颖(1960—),女,辽宁大连人,清华大学副教授,研究方向为超精密加工工艺与装备、精密驱动与控制、CAD/CAM/CAPP,(E-mail)liucy@tsinghua.edu.cn。
(编辑李秀敏)

