任意正多边形小孔夫琅禾费衍射成像探讨

宋易知

(北京师范大学 物理学系，北京 100875)

任意正多边形小孔夫琅禾费衍射成像探讨

宋易知

(北京师范大学 物理学系，北京 100875)

对夫琅禾费衍射积分进行了理论推导，基于夫琅禾费衍射积分公式的一般形式，推导出了一种对任意正多边形小孔夫琅禾费衍射情况的计算方法，并利用Matlab软件进行计算机模拟，做出了只用1个函数文件即可计算出所有可能的多边形小孔夫琅禾费衍射成像的尝试.

正多边形小孔；夫琅禾费衍射；Matlab

1 理论基础

光的衍射现象能体现光的波动性，即光在直线传播中遇到圆孔、小球、直边等障碍物时，不被挡住反而绕到其后面传播，进入光强本应为零的暗区[1-2]. 惠更斯-菲涅耳原理以波动理论解释光如何传播，指出波阵面上每一点均为次波源，这些次波的包络面即为新波面.

(1)

其中C为比例系数,K(θ)为倾斜因子[当θ增大时，K(θ)缓慢减小],Σ为平面波的1个波面[3].

(2)

(3)

在通常的光学处理系统中，z应远远大于衍射小孔和观察区域的最大线度，且从P到Q点的距离应远远大于光的波长，即r≫λ，相当于用平面波的振幅替代球面波前在观察平面上产生的复振幅[3]. 易推知θ应为小量，则有

K(θ)=cosθ≈1 .

(4)

虽然(3)式分母中的r可以直接用z代替，但不能忽略的是，当λ很小时，k值很大，指数中的r的微小误差可能引入远大于2π的相位变化，使之不可以直接用z代替. 对其做二项式展开[4]

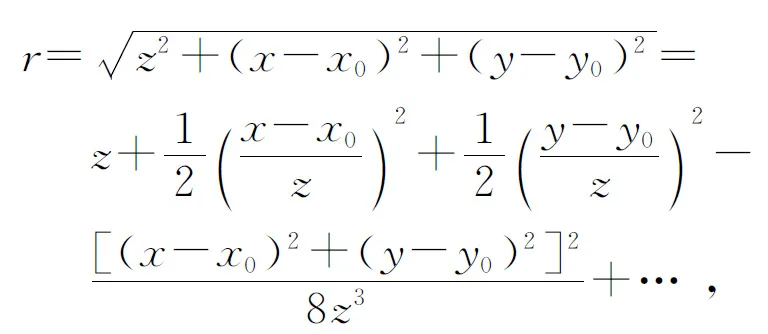
(5)

保留展开式的前两项，有

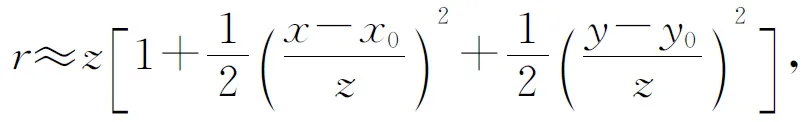
(6)

于是得到了菲涅耳衍射积分

(7)

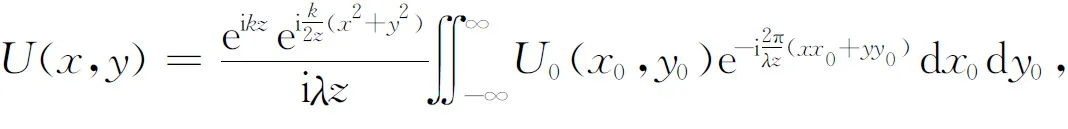
(8)

即在夫琅禾费衍射区内观察平面上的夫琅禾费衍射积分公式的一般形式.

2 计算原理

2.1 计算思路

如图1所示，由于正多边形的中心对称性，对于正L边形的小孔，只需要计算出1个小三角形的衍射场分布，将其进行L-1次坐标旋转变换，随后将其全部相加，就能获得任意正多边形小孔的夫琅禾费衍射成像. 此前的衍射成像模拟程序都局限在某个特定形状小孔上，而在这种思路的指导下， 本文做出了只用1个函数文件计算出所有可能的多边形小孔夫琅禾费衍射成像的尝试.

图1 正多边形由多个小三角形组成

2.2 等腰三角形孔的夫琅禾费衍射

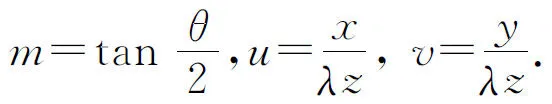
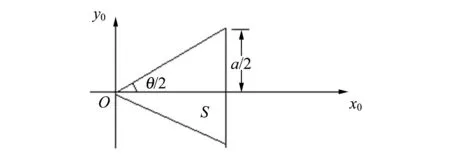
图2 等腰三角形孔

(9)

2.3 正多边形孔的夫琅禾费衍射

如果衍射屏为边长为a的正n边形孔(如图3)，则以其几何中心为原点，建立坐标系. 由于S=S1+S2+…+Sn，这样夫琅禾费衍射积分就可以分别在这n个三角形区域进行，由于这n个三角形是全等的，其积分结果应当对称. 可从S1的衍射结果式(9)出发，依次绕z轴旋转θ角，即对式(9)依次作下列坐标变换：

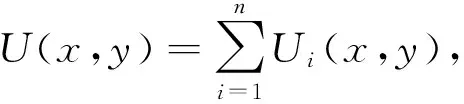
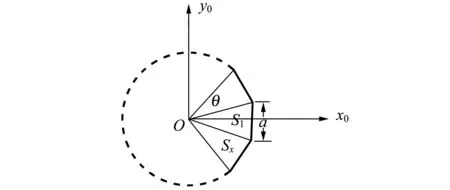
图3 正n边形孔

由此，得到了正多边形小孔的夫琅禾费衍射的计算方法. 原则上存在任意多边形孔的夫琅禾费衍射公式，但是将每个都计算出来极其繁琐且不具操作性. 因此，不妨考虑用计算机程序模拟的方法解决这个问题.

3 Matlab模拟

3.1 程序

根据以上计算分析编写夫朗禾费任意多边形小孔衍射仿真函数文件(运行环境：Matlab R2014b)[6]:

function dbx(L) %L是边数

the=pi*(L-2)/L; %多边形的外角

m=tan((pi-the)/2); %等腰小三角形顶角的1/2

a=3e-5;

lamda=500e-9; %光的波长

z=6; %衍射屏到观察屏的距离

k=2*pi/lamda;

h=a/(2*m*lamda*z);

x=-1∶0.005∶1;

y=-1∶0.005∶1;

for i=1∶1∶401

for j=1∶1∶401

for n=1∶L

C=a*exp((-1)^(1/2)*k*z)*exp((-1)^(1/2)*k*((x(i))^2+(y(j))^2)/2/z)/(4*pi*m*y(j));

alpha=h*(x(i)+m*y(j));

beta=h*(x(i)-m*y(j));

E1(n,i,j)=C*(exp(-(-1)^(1/2)*pi*alpha)*sin(alpha)/alpha-exp(-(-1)^(1/2)*pi*beta)*sin(beta)/beta);%单个小三角形的衍射场

u(i)=x(i); %x和y分别转过一角度

x(i)=x(i)*cos(the)+y(j)*sin(the);

y(j)=-u(i)*sin(the)+y(j)*cos(the);

end

E(i,j)=sum(E1(∶,i,j)); %L个小三角形相加

I(i,j)=abs(E(i,j))^2; %求光强

end

end

m=max(I(∶));n=min(I(∶));I0=(I-n)/(m-n);

figure(1)

imshow(I0) %画图

figure(2)

mesh(I)

3.2 运行结果

3.2.1 正三角形小孔

在指令窗口输入“〉〉dbx(3)”得到图像如图4所示.

3.2.2 正四边形小孔

在指令窗口输入“〉〉dbx(4)”，得到图像如图5所示.

(a)

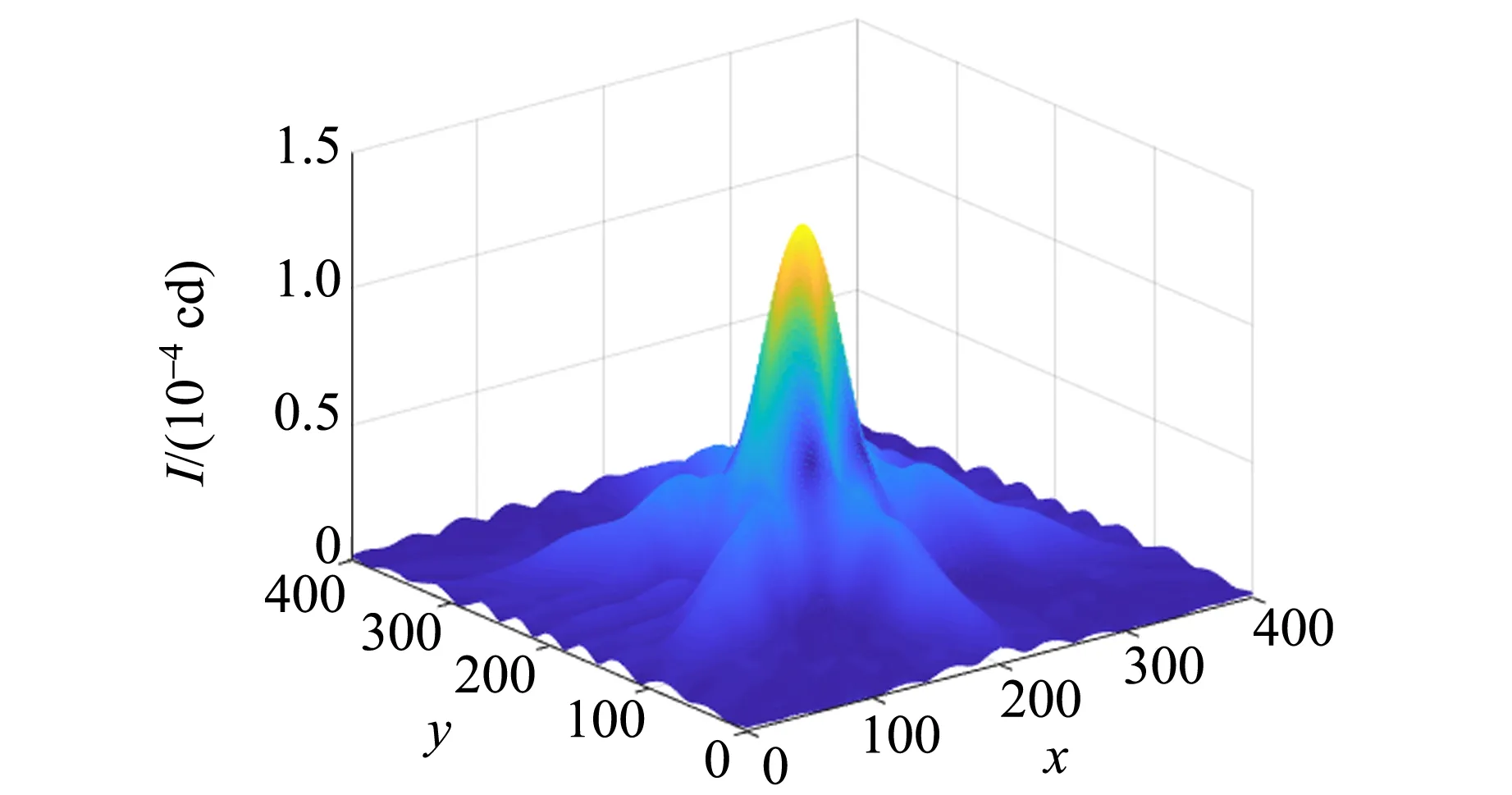
(b)图4 正三角形小孔衍射图样

(a)

(b)图5 正四边形小孔衍射图样

3.2.3 正五边形小孔

在指令窗口输入“〉〉dbx(5)”，得到图像如图6所示.

3.2.4 正六边形小孔

在指令窗口输入“〉〉dbx(6)”，得到图像如图7所示.

(a)

(b)图6 正五边形小孔衍射图样

(a)

(b)图7 正六边形小孔衍射图样

4 结束语

在当今社会，计算机技术迅猛发展并日臻完善，基于Matlab 的计算机模拟技术对物理研究的帮助日趋显著. 由计算机模拟结果可见，衍射图样为旋转对称图形，且在正多边形各边的垂直方向上光强较强；边数越多，光强较强的区域越密集. 不难推断，当n→∞时，光强分布为圆形亮斑外套着明暗相间的圆环，即圆孔的夫琅禾费衍射图样. 可以看到，计算机模拟的正五边形的衍射图样由于排布十分密集，已经接近圆孔的夫琅禾费衍射图样.

致谢：衷心感谢计算物理老师彭芳麟教授的教导！

[1] 姚启钧. 光学教程[M]. 5版. 北京：高等教育出版社，2014.

[2] 加塔克.光学[M]. 梁铨廷，胡宏章，译. 北京：机械工业出版社，1984:74-85.

[3] 厉江帆，姜宗福，黄春佳，等. 夫琅禾费衍射公式的一般形式[J]. 大学物理，2003，22(11):9-14.

[4] 于爱军. 光的多边形衍射的计算机模拟[D]. 大连：大连理工大学，2007.

[5] Joseph W G. Introduction to Fourier optics [M]. 北京：电子工业出版社，2006:59-67.

[6] 彭芳麟. 计算物理基础[M]. 5版. 北京：高等教育出版社，2010.

DiscussionontheFraunhoferdiffractionimagingofarbitraryregularpolygonhole

SONG Yi-zhi

(Department of Physics, Beijing Normal University, Beijing 100875, China)

Based on the general form of Fraunhofer diffraction integral, the calculative method to analyze arbitrary regular polygon Fraunhofer diffraction was put forward. Using the Matlab software, computer simulation was carried out, attempting to get all possible Fraunhofer diffraction imaging of the regular polygon hole with just one function file.

regular polygon hole; Fraunhofer diffraction; Matlab

O436.1

A

1005-4642(2017)11-0048-04

2017-06-05；修改日期2017-07-07

宋易知(1998-)，女，四川乐山人，北京师范大学物理学系2014级本科生.

[责任编辑：郭 伟]