基于Nyquist图研究铁基非晶薄带巨磁阻抗效应的非线性

许志强，赵乾坤

(郑州轻工业学院 电气信息工程学院，河南 郑州 450002)

基于Nyquist图研究铁基非晶薄带巨磁阻抗效应的非线性

许志强，赵乾坤

(郑州轻工业学院 电气信息工程学院，河南 郑州 450002)

测量了铁基非晶薄带巨磁阻抗效应的阻抗实部和虚部并且计算出磁导率的实部和虚部，通过磁导率的非线性解释了巨磁阻抗效应的非线性原因,并且利用Nyquist图推出磁导率等效电路模型，指出磁导率等效电路模型中的LC共振频率是解决磁导率非线性的关键. 研究结果表明：在激励电源横向磁化和外加磁场纵向磁化的过程中，非晶薄带磁导率的变化无规则，导致非晶薄带的巨磁阻抗效应呈现非线性变化. 当激励频率在5 MHz、纵向磁场发生改变时，磁损耗角依然保持不变，磁导率与纵向磁场的非线性关系转化为磁导率模值与纵向磁场的关系，通过实验数据可以拟合出纵向磁场与磁导率的函数关系.

巨磁阻抗效应；非线性；Nyquist图；磁导率；磁损耗角；等效电路模型

巨磁阻抗效应(Giant magneto-impedance,GMI)是指当丝状或带状软磁材料通入交流电时，材料阻抗随磁场变化而变化的现象. 名古屋大学K. Mohri等人于1992年用内圆水纺法喷制出直径为125 μm的CoFeSiB软磁非晶丝材料，在CoFeSiB非晶丝中通入交变电流，感抗值会随着外部纵向磁场的变化而变化，当外部磁场增加到0.8 kA/m时，非晶丝材料两端电压值比不施加外部纵向磁场时的电压值明显变小，感应电压变化量高达75%[1-3]. 随后巴西Machado等人对CoFeSiB系列非晶丝做了深入研究，他们发现了非晶丝中的磁电阻效应[4]. 综合考虑了上述的磁电感和磁电阻效应，日本学者Panina和西班牙学者Velazquez认为二者系出同源，本质上都是在外部磁场影响下阻抗值随之变化的物理效应，统称为磁阻抗效应[5-6]. 当非晶态合金材料通入高频电流后，阻抗变化随着磁场变化高达12%～120%，因此该现象又被称为巨磁阻抗效应，其高灵敏度优点使得利用GMI效应开发新型磁传感器引起研究人员的广泛关注. 近几年的相关研究中，有关GMI效应的研究主要是围绕材料的结构、工艺、尺寸和其他相关参量对其GMI效应的影响方面展开的. 自1993年开始，国内研究人员对Fe-Si-B系列材料展开研究，成功研制出了真空快淬设备[7]. 鲍丙豪等人对GMI效应在微型电流传感器的应用做了许多研究[8-9]；韩冰等人研制了基于GMI效应的阵列式探头电流传感器，此传感器展现出了较好的温度稳定性，并同时具备出色的线性度和灵敏度[10]. 周泽魁等人设计了GMI效应电涡流检测系统[11]. 本研究通过分析与巨磁阻抗效应有关的参量，测量出铁基非晶薄带巨磁阻抗效应的阻抗实部和虚部并计算出磁导率实部和虚部，提出巨磁阻抗效应非线性的原理，并通过分析磁导率的非线性来解释巨磁阻抗效应的非线性，同时利用Nyquist图推出磁导率等效电路模型，提出磁导率等效电路模型中的LC共振频率可解释磁导率非线性.

1 铁基非晶薄带巨磁阻抗效应特性

GMI效应的描述采用电阻变化率来表示，通常定义为

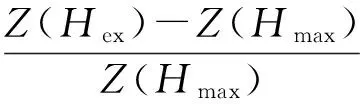
式中，Z(Hex)为外部磁场Hex作用下非晶薄带的阻抗值，Z(Hmax)为外部磁场Hex作用下非晶薄带达到饱和时的阻抗值.

1.1 磁化过程

磁化过程分为横向磁化和纵向磁化. 当非晶薄带通入交流电时，根据安培定则一可知，非晶薄带周围生成环形磁场并产生横向磁化过程；当非晶薄带外面缠绕线圈通入电流时，根据安培定则二可知，线圈生成平行于非晶薄带的磁场，非晶薄带纵向产生磁化过程.

1.2 巨磁阻抗效应的表征

当给非晶薄带通交流电，由电磁理论及边界条件，非晶带阻抗表示为[12]

(1)

式中，Rdc为非晶薄带直流电阻，a为非晶薄带厚度，k满足

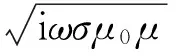
(2)

式中，i为虚部，ω为流过非晶薄带的交流电的角频率，σ为非晶薄带电导率，μ0和μ分别为真空磁导率及材料的相对有效磁导率.

由式(1)～(2)可知，在一定频率下，阻抗Z和唯一变量μ有关，μ是研究巨磁阻抗效应非线性的关键.

1.3 相对有效磁导率的表征

相对有效磁导率μ为复数，定义μ=μ′-jμ″. 由于磁导率虚部的存在，将引起材料磁化过程中不断消耗能量. 根据平均能量密度损耗公式、储能公式、能量守恒定律和安培环路定理可以得到[13-14]：

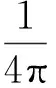
(3)

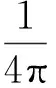
(4)

式中，L为非晶薄带的长，a为非晶薄带的厚，b为非晶薄带的宽，Z′和Z″分别为非晶薄带的阻抗的实部和虚部.

由式(3)～(4)可知，在一定频率下，相对有效磁导率μ的虚部与材料阻抗的实部成线性关系，μ的实部与材料阻抗的虚部成线性关系.

通过上述分析，实验的重点是测量材料阻抗Z的实部Z′和虚部Z″，然后计算μ′和μ″.

2 铁基非晶薄带阻抗参量获取

实验所用铁基非晶薄带产自佛山市中研非晶科技股份有限公司. 取实验样本薄带长L=19 mm，厚a=0.1 mm，宽b=15 mm. 薄带的阻抗用KEYSIGHT公司的E4990A阻抗分析仪测量，所用夹具为16047E，测量前进行引线补偿. 外磁场由亥姆霍兹线圈产生. 实验中测量非晶薄带在外磁场纵向磁化过程中(频率范围104～108Hz)的实部Z′和虚部Z″. 根据式(3)～(4)将阻抗数据转换为与磁化过程直接相关的磁导率数据，对磁导率数据进行分析.

3 磁导率的频率特性

图1为外加磁场Bex=0 mT和外加磁场Bex=20 mT时磁导率的实部随激励电流频率的变化曲线，图2为磁导率的虚部随激励电流频率的变化曲线.

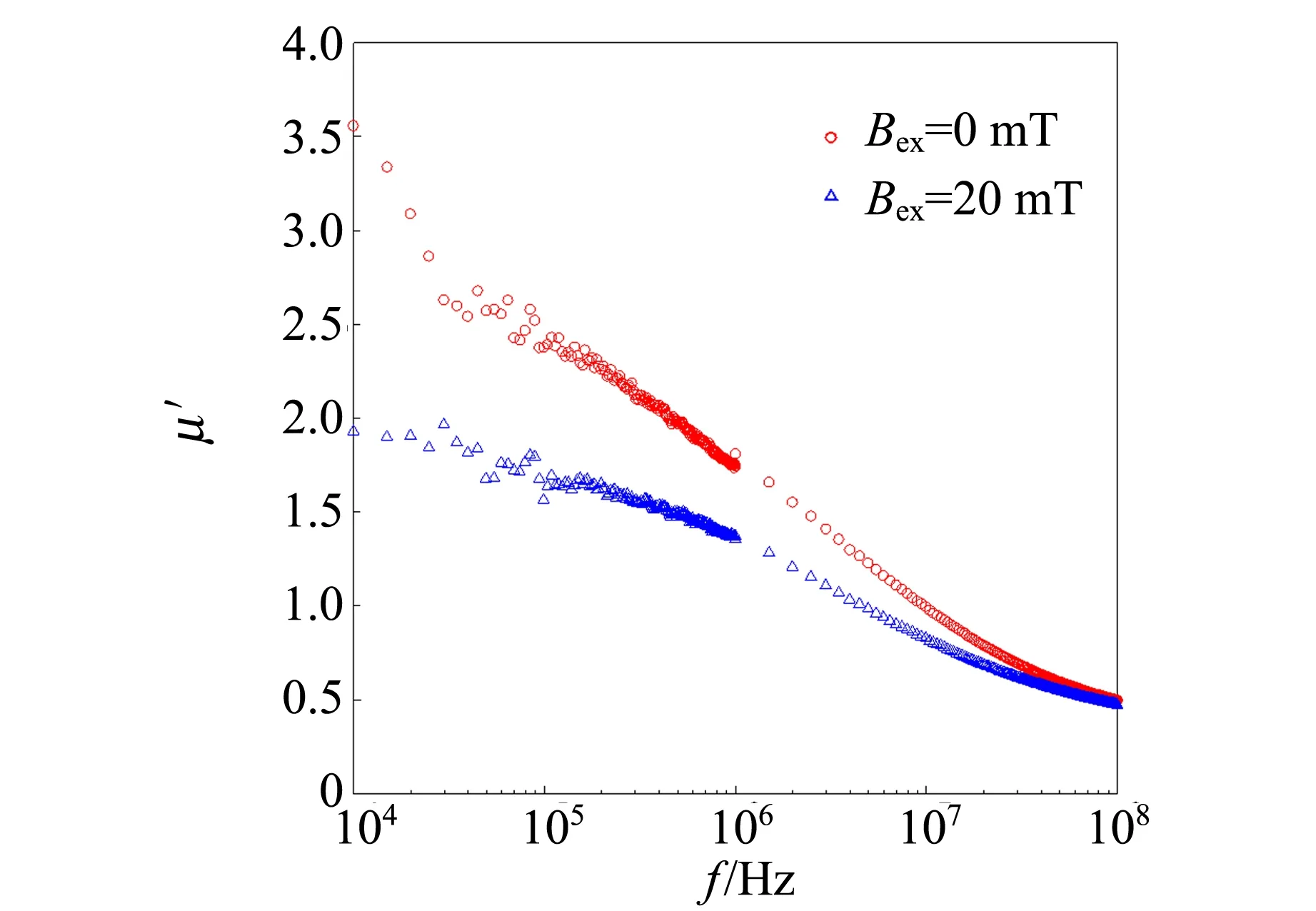
图1 不同外磁场下磁导率实部与频率的关系

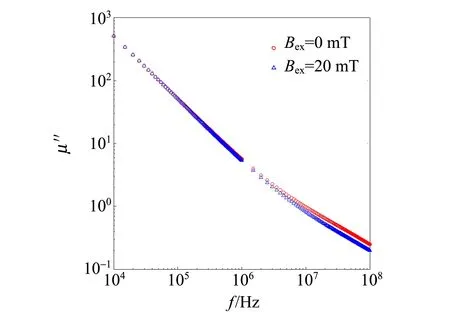
图2 不同外磁场下磁导率虚部与频率的关系

从图1中可以看出在较低频率且无外加纵向磁场的情况下，磁导率的实部μ′值最大，当频率继续增大时，μ′出现一降低的弛豫过程，最后在108Hz趋近常量. 外加纵向磁场后的磁导率实部频率特性与未加磁场类似，但是弛豫频率略有增加，外加直流磁场后磁导率的实部在较低频率下变小，当频率高于106Hz时下降减缓. 从图2可以看出磁导率的虚部在施加磁场和不施加磁场的情况下,2条曲线基本重合，都随频率的增加逐渐减小.

为了进一步分析巨磁阻抗效应，实验中引入交流阻抗谱Nyquist图. 图3为不同外磁场下磁导率实部与虚部的Nyquist图.

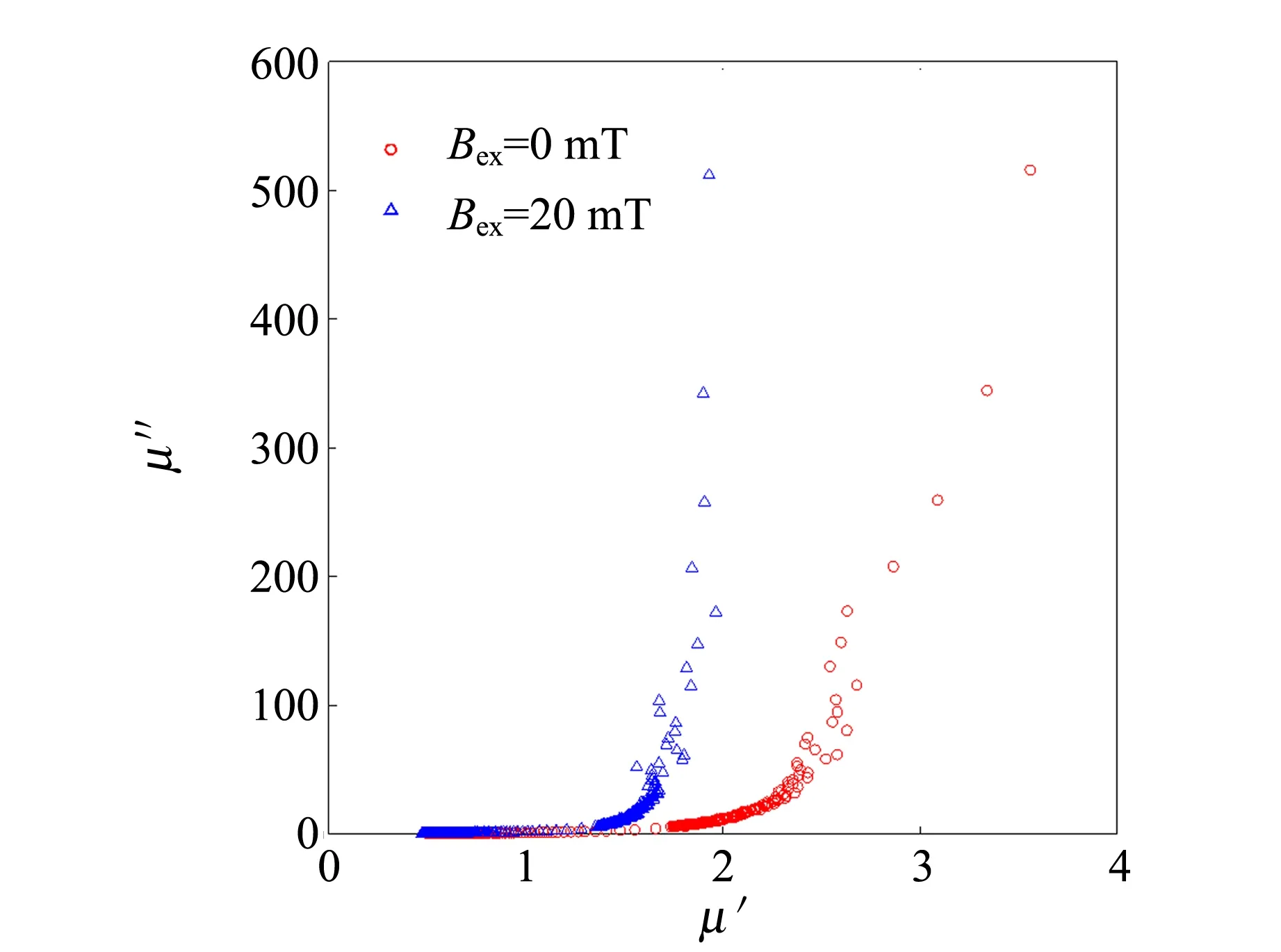
图3 不同外磁场下磁导率的Nyquist图

4 磁导率非线性分析

假设外加激励电源Iac在一定频率下工作并产生横向磁化，外加纵向磁场Bex从0到20 mT，磁导率从Bex=0 mT的A点移动到Bex=20 mT的B点(如图4)，C点为Bex∈(0,20)区间上对应的任意一条磁导率曲线上的点，根据数学中的夹逼准则和区间套定理，C点一定在磁导率曲线Bex=0 mT和Bex=20 mT之间，并且C点实部最终趋近于同一常量(图3).

为了解释磁导率非线性原理，不妨假设磁场变化ΔB引起磁导率从A点移动到C点，相同的磁场变化ΔB引起磁导率从C点移动到B点，定义磁导率向量OA，OC和OB的向量角分别为θA，θC，θB，又叫磁损耗角[15]δ=actan (μ″/μ′) . 产生非线性的原因来源2方面：

1)向量模值的非线性，即

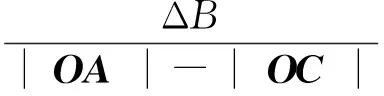
2)磁损耗角的非线性，即

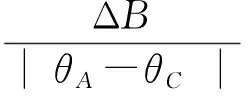
由式(1)～(2)可知，磁导率的非线性导致巨磁阻抗效应的非线性，为了研究巨磁阻抗效应，必须研究磁导率的这2个非线性因素.

研究中用保持磁损耗角一致的方法来分析磁导率的非线性. 如图4中的向量OA′,OC′和OB′近似在一条直线上，即磁损耗角近似相等，这条近似的直线可以通过实验数据找到，这种方法简化了磁场Bex与磁导率μ的关系. 通过实验数据可知，磁损耗角近似相等的这条直线对应的激励电源Iac的频率是5 MHz.

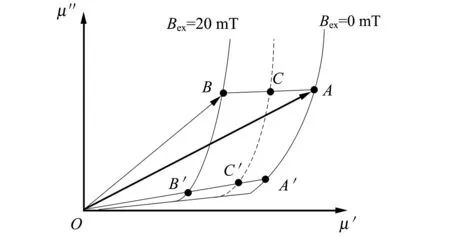
图4 磁导率非线性原理分析图

由上述分析得出，当激励电源Iac在5 MHz工作时，磁导率μ的非线性问题简化为外加磁场Bex与磁导率模值的关系，最后通过实验数据拟合出|μ|=F(Bex)函数关系式.

5 用Nyquist图确立磁导率电路模型

从上述分析可知，研究巨磁阻抗效应重点是研究磁导率μ在磁场B作用下的函数关系. 在函数μ=F(B)中，通过Nyquist图确立F的电路模型. 下面列出研究中用到的3个Nyquist图.

5.1 RC串联电路Nyquist图

如图5所示，RC串联电路阻抗Z表达式为

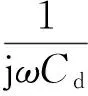
(5)

图5 RC串联电路模型

图6为RC串联电路Nyquist图，Z′为常量RL，而Z″随f而改变，f越大，Z″越小. 因此，理想RC串联电路Nyquist图是1条与纵轴平行的直线，直线与轴相交点的横坐标等于RL.

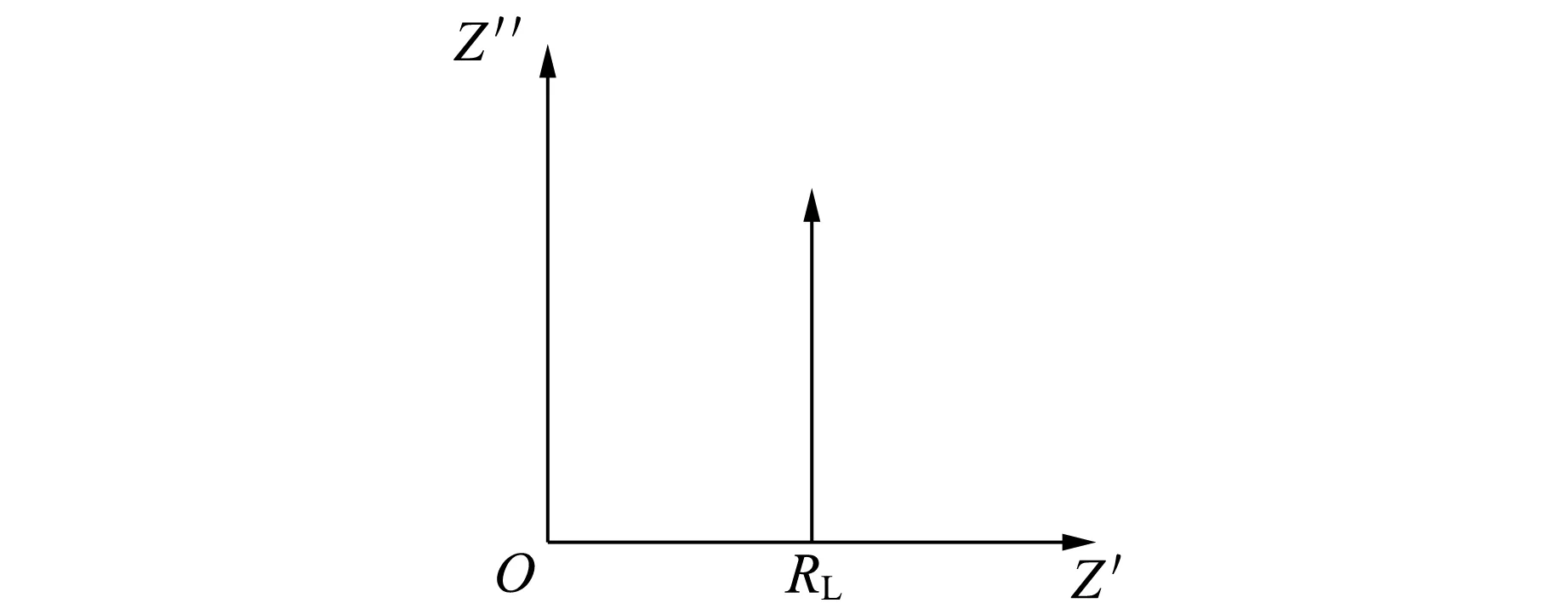
图6 RC串联电路Nyquist图

5.2 RC并联电路与RL并联电路Nyquist图

如图7所示，RC并联电路阻抗Z表达式为

(6)

对式(6)整理可得

(7)

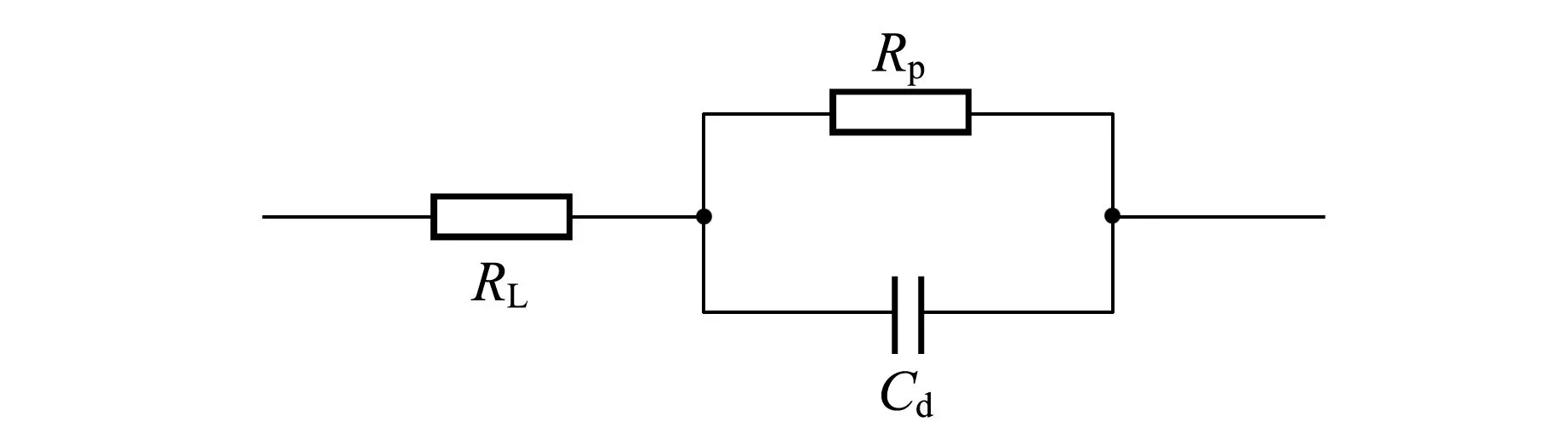
图7 RC并联电路模型

图8为RC并联电路Nyquist图，其圆心在Z′轴上，半径为Rp/2，电阻RL是原点到A点的距离，由于Z′和Z″的取值范围，此圆分布在第一象限.

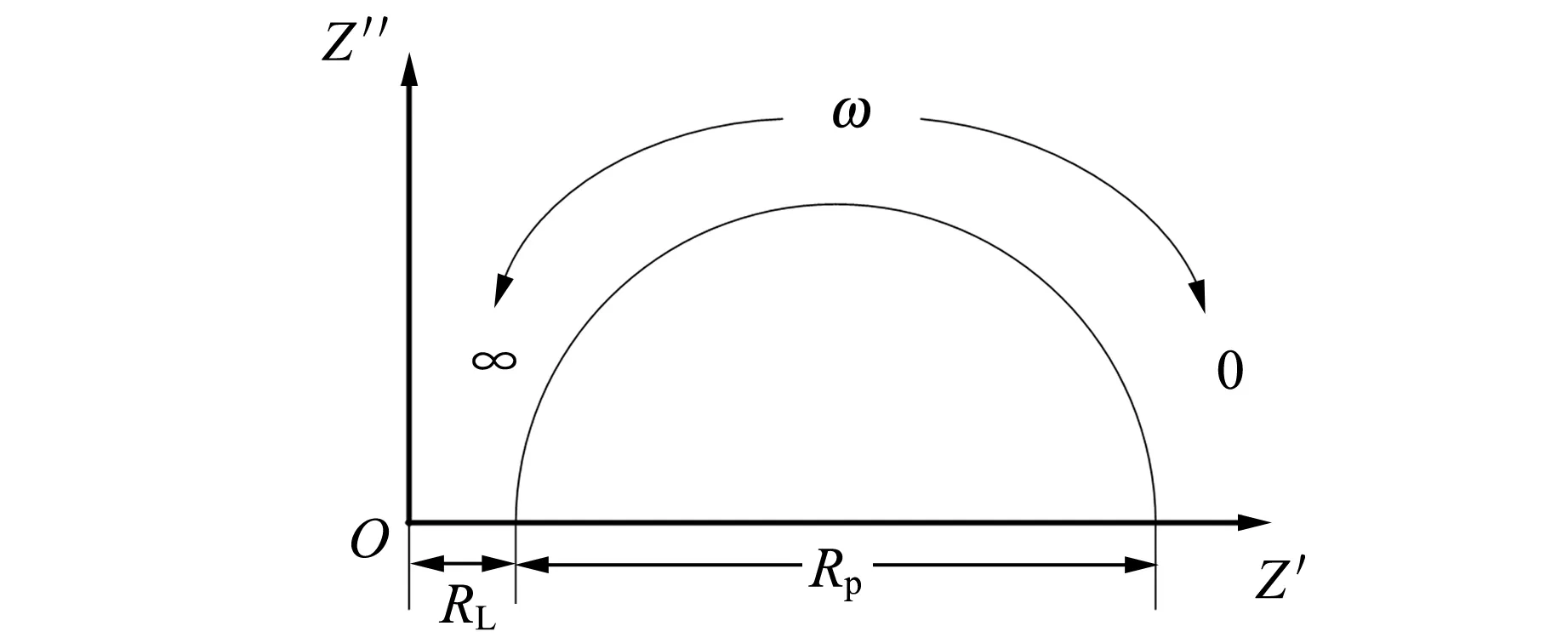
图8 RC并联电路Nyquist图

RL并联电路Nyquist图与RC并联电路Nyquist图关于Z′轴对称，分布在第四象限.

5.3 RC串并联混合电路Nyquist图

如图9所示，混合电路阻抗Z′和Z″表达式为

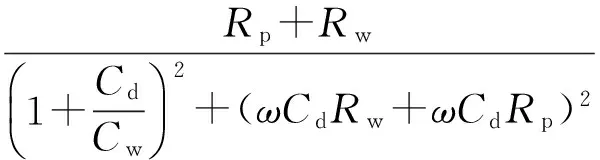
(8)

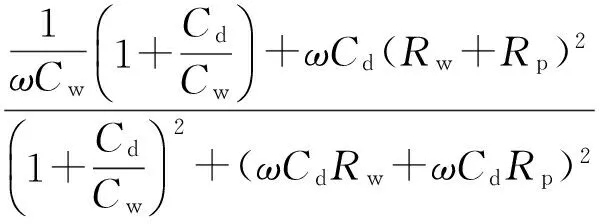
(9)

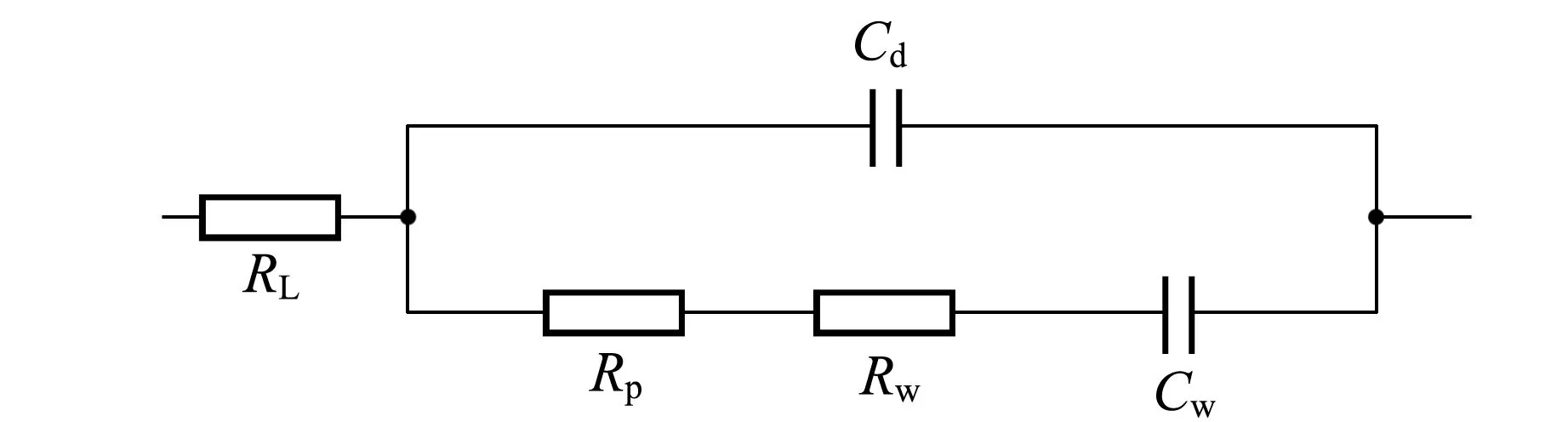
图9 RC串并联混合电路模型

图10为RC串并联混合电路Nyquist图，分布在第四象限.

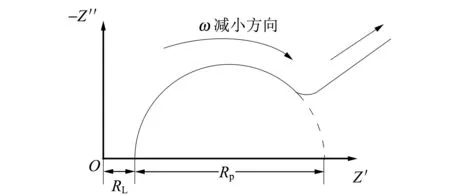
图10 RC串并联混合电路Nyquist图

RL串并联混合电路Nyquist图与图10关于Z′轴对称，分布在第一象限.

5.4 函数F的电路模型

从图3中可以得知，在中低频(5 MHz以下)时，磁导率的Nyquist图存在垂直纵轴的区间段，这与图6的RC串联电路Nyquist图类似，由此可以推出函数F的电路模型中包含一部分RC串联电路模型；在中高频(5 MHz以上)时，磁导率的Nyquist图逐渐靠近横轴，并且慢慢平行于横轴，这可以由图8推出的RL并联电路Nyquist图和图10推出的RL串并联混合电路Nyquist图叠加而形成，推出函数F的电路模型包含RL并联电路和RL串并联混合电路. 由此可以推出函数F的电路模型是由RC串联、RL并联和RL串并联混合电路组成，如图11所示.

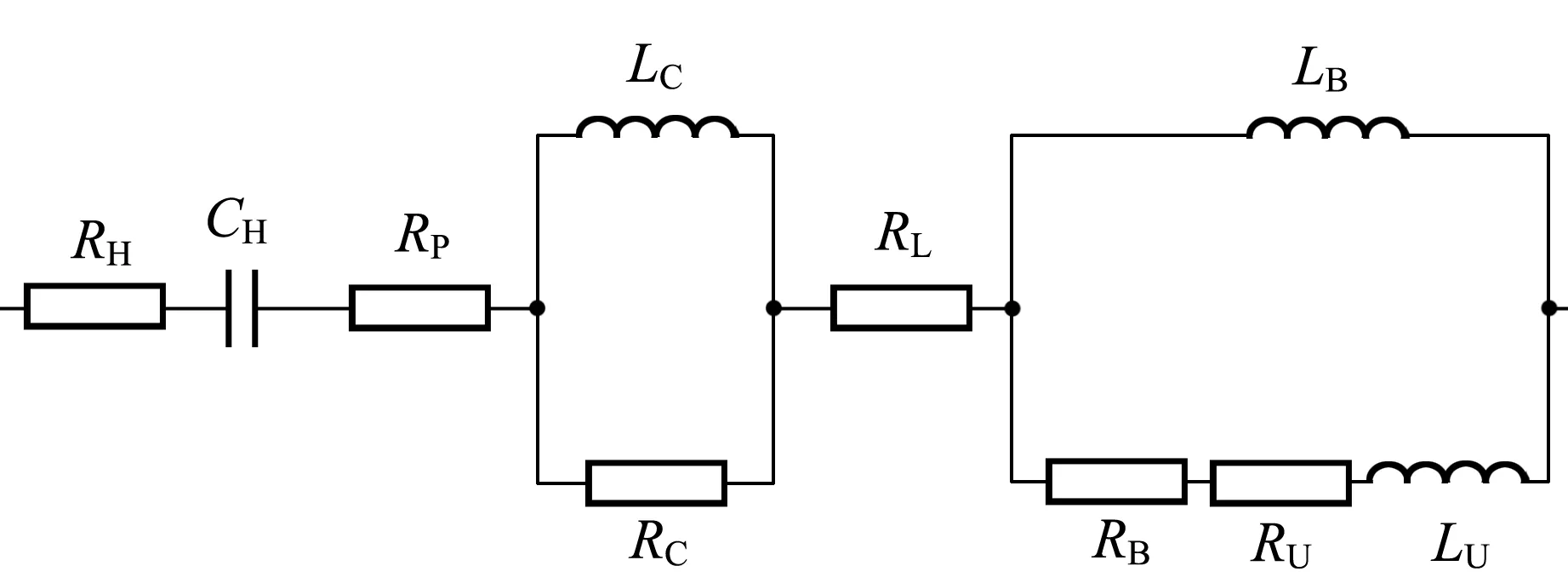
图11 函数F的等效电路模型

磁导率等效电路模型中的电容与电感存在共振频率，通过阻抗分析仪测得的数据可以计算出此共振频率在5 MHz，与之前分析得出的结论一致.

值得注意的是，研究过程中测得非晶薄带的频率共振点与实验中采用的补偿导线以及补偿导线与非晶薄带的连接方式有关系. 这点很容易理解：补偿导线改变了非晶薄带的电感值，而连接方式改变了电容值. 因此，工程中运用此方法制作传感器时可以采用模糊数学的思路研究频率共振点.

在中低频交流激励下非晶薄带以磁畴位移为主[12]，外加磁场对磁畴的位移运动有影响，使磁导率的实部出现大幅度降低(如图3)，因此磁畴位移与RC串联电路模型有关；在中高频时以磁畴转动为主[12]，磁畴转动与RL并联联电路模型有关. 由此可得函数F等效电路模型各个参量的特性如表1所示.

表1 等效电路模型各个参量的特性

6 结 论

巨磁阻抗效应的非线性是由磁导率的非线性引起，通过实验数据，分析了产生磁导率非线性的原因，采用保持磁损耗角一致的方法阐述了解决磁导率非线性问题的方法. 通过Nyquist图推出磁导率等效电路模型，从等效电路模型角度解释磁导率的非线性. 研究结果表明：在激励电源横向磁化和外加磁场纵向磁化的过程中，非晶薄带磁导率的变化无规则，导致非晶薄带的巨磁阻抗效应呈现非线性变化. 当激励频率在5 MHz时，纵向磁场发生改变，磁损耗角依然保持不变，磁导率与纵向磁场的非线性关系转化为磁导率模值与纵向磁场的关系，通过实验数据拟合出纵向磁场与磁导率的函数关系. 最后从磁畴的角度简要概括了等效电路模型中每个元件特性，为磁畴学和电路学的联系提供参考.

[1] Valenzuela R, Fessant A, Gieraltowski J, et al. Effect of the metal-to-wire ratio on the high-frequency magnetoimpedance of glass-coated CoFeBSi amorphous microwires [J]. Sensors & Actuators A Physical, 2008,142(2):533-537.

[2] Machado F L A, Silva B L D, Rezende S M, et al. Giant ac magnetoresistance in the soft ferromagnet Co70.4Fe4.6Si15B10[J]. Journal of Applied Physics, 1994,75(10):6563-6565.

[3] Shen L P, Uchiyama T, Mohri K, et al. Sensitive stress-impedance micro sensor using amorphous magnetostrictive wire [J]. Transactions on Magnetics, 1997,33(5):3355-3357.

[4] Phan M H, Peng H X. Giant magnetoimpedance materials: Fundamentals and applications [J]. Progress in Materials Science, 2008,53(2):323-420.

[5] Almeida T M D, Piedade M S, Sousa L A, et al. On the modeling of new tunnel junction magnetoresistive biosensors [J]. IEEE Transactions on Instrumentation & Measurement, 2010,59(1):92-100.

[6] Panina L V, Mohri K. Mechanism of the magneto-impedance effect in negative magnetostrictive amorphous wires [J]. IEEE Translation Journal on Magnetics in Japan, 1994,9(5):34-39.

[7] 王晓美. 基于非晶丝巨磁阻抗效应的微型磁传感器技术研究综[D]. 北京:中国地震局地球物理研究所,2005.

[8] 鲍丙豪,李长生. FeCuNbSiB单纳米晶磁芯双绕组新型电流传感器[C]//第一届长三角地区传感技术学术交流会论文集. 上海:2004.

[9] 鲍丙豪,丁建宁,李长生. FeCuNbSiB单纳米晶环形磁心双绕组新型微电流传感器[J]. 电力系统自动化,2004,28(15):104-107.

[10] Han B, Zhang T, Zhang K, et al. Giant magnetoimpedance current sensor with array-structure double probes [J]. IEEE Transactions on Magnetics, 2008,44(5):605-608.

[11] 龚翔. 电涡流检测系统开发及正向问题研究[D]. 杭州:浙江大学,2013.

[12] 鲍丙豪. 磁芯气隙中串联层叠非晶带GMI效应电流传感器[J]. 仪器仪表报,2009,30(9):1861-1865.

[13] 刘江涛,周云松,王艾玲，等. 三明治结构与同轴电缆结构磁性材料巨磁阻抗效应的理论研究[J]. 物理学报,2003,52(11):2859-2864.

[14] 王艾玲,刘江涛,周云松，等. 各向异性场对三明治膜巨磁阻抗效应的影响[J]. 物理学报,2004,53(3):905-910.

[15] 袁帅,张吉涛,许志强，等. 剩磁效应对SmFe2/PZT多铁异质结构动态磁机特性及磁场传感特性的影响[J]. 河南农业大学学报,2017,51(2):177-183.

NonlinearityofGMIeffectiniron-basedamorphousribbonresearchedbyusingNyquistfigure

XU Zhi-qiang， ZHAO Qian-kun

(College of Electric and Information Engineering，Zhengzhou University of Light Industry， Zhengzhou 450002， China)

The real and imaginary parts of the impedance of giant magneto-impedance effect were measured, and the real and imaginary parts of the permeability were calculated. The principle of the nonlinearity of GMI effect was proposed based on the nonlinearity of the permeability, and theLCresonant frequency of EC model of permeability by Nyquist figure was pointed out．The results showed that the irregularity of the changes of permeability of iron-based amorphous ribbon in transverse and longitudinal magnetization process led to nonlinear changes of the GMI effect．Under 5 MHz excitation, the magnetic loss angle remained consistent. The nonlinear relation between permeability and longitudinal magnetic field was transformed into the relationship between modulus value of permeability and longitudinal magnetic field, and the function of permeability and the longitudinal magnetic field was obtained by fitting the experimental data．

giant magneto-impedance effect; nonlinearity; Nyquist figure; permeability; magnetic loss angle; EC model

TM936．4

A

1005-4642(2017)11-0007-06

2017-06-16；修改日期2017-07-10

国家自然科学基金项目(No.61503344)

许志强(1982-)，男，河南郑州人，郑州轻工业学院电气信息工程学院2015级硕士研究生，从事电流传感器与测控技术的研究.

赵乾坤(1990-)，男，河南焦作人，郑州轻工业学院电气信息工程学院2015级硕士研究生，从事电能质量的研究.

[责任编辑：任德香]