非均匀土壤矩形接地网优化设计

李慧奇，王璐，陈明，邢琳，张大雨

（1.华北电力大学河北省输变电设备安全防御重点实验室，河北保定071003；2.国网河北省电力公司经济技术研究院，石家庄050021）

0 引 言

接地网是变电站安全运行的重要保证，其接地性能一直是研究的热点问题。接地网在变电站安全运行中，不仅为变电站内各种电气设备提供一个公共的电位参考地，还能在接地网遭受雷击或电力系统发生故障时，迅速排泄故障电流，降低变电站的地电位升。接地网接地性能的优劣直接关系到变电站内工作人员的人身安全和各种电器设备的安全和正常运行［1］。

关于接地网优化的研究，最早由德国Sverak提出的接地网不等间距布置理论［2］，随后加拿大科学家Dawalibi在在接地网均压带优化布置进行了研究［3-4］。1986年，重庆大学陈先禄教授在国内率先提出了均匀土壤环境下利用不等间距布置接地网均压带进行优化。曾嵘、何金良等教授对接地网在高频环境下的性能进行了研究，司马文霞、文习山等教授利用遗传算法对接地网均压带进行了优化。清华大学高延庆教授对非均匀土壤环境下的接地网指数布置最优压缩比进行了研究。曹晓彬、胡劲松率先对矩形接地网进行了优化设计［5-10］。

研究表明，接地网指数布置并不是接地网最优布置方案，由于指数函数有快速衰减的数学特征，当对多根水平接地体进行优化布置时，会出现边缘网孔过于密集的情况，从而导致边缘网孔导体不能充分利用。

本文通过分析不同反射系数、接地网面积和上层土壤厚度因素对最优系数的影响，得出最优系数优化公式，并将其应用到非均匀土壤矩形接地网优化中。通过和其他方法的计算对比，得出利用本文计算方法优化的接地网，使最大接触电压降低12%左右。确定变电站接地网性能优劣的电参数有很多，其中接触电压是最难满足安全要求的，所以本文以接触电压达到安全要求为优化目标，研究接地网的优化布置方案。

1 接地体的仿真分析

1.1 仿真模型建立

首先考虑正方形地网的优化，即a=b的情况，设a=b=100 m，n根垂直于边长的均压带将接地网一边分为n-1段，每段从左至右分别编号，定义（i=1，2……，n-1）为第i段接地体占接地网边长总长的占比。图1为不等间距分布接地网图，表1为当分段数不同时最优布置方案。

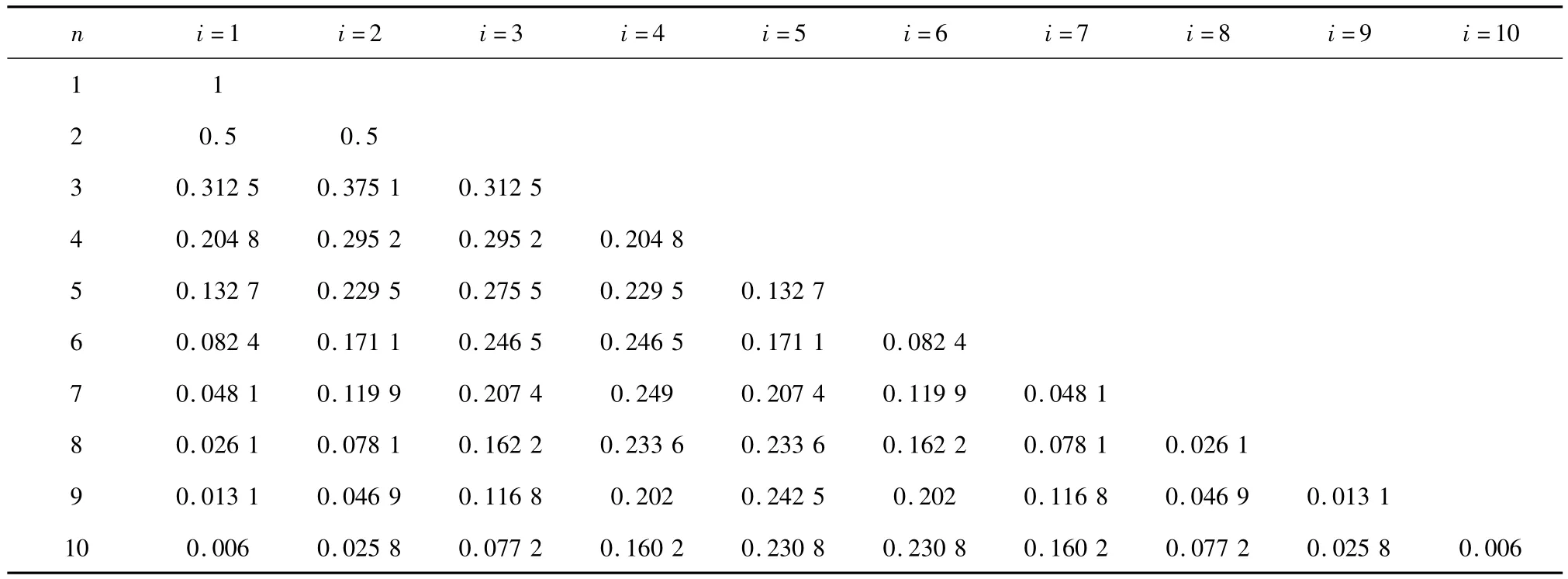
表1 当分段数不同时最优布置方案Tab.1 Optimal ground scheme in different segments

图1 不等间距分布接地网图Fig.1 Unequally spaced grounding grid

1.2 结果分析

增加每边上导体的数量，调整导体的位置，假设每个网孔的最大接触电压为，记录下每个网孔相等时候的每段所占百分比如表1所示。定义第i段所占比为Mi，经过拟合得到：

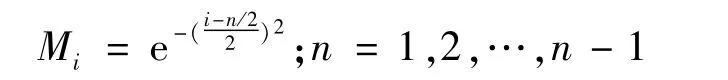
当改变接地网面积和均压带的数量时，进行拟合，发现公式中只有指数幂位置中的分母变化，所以假设最优拟合公式为：

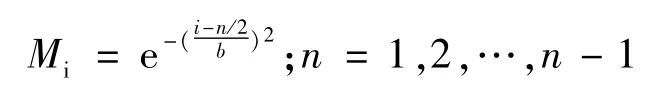
可以将b视为为参数，只要得到最优的b值，就可得到接地网的最优的布置方案。

2 各种因素对最优系数的影响

2.1 上层土壤厚度

最优参数值与上层土壤厚度h及反射系数k的关系如图2所示。

图2 L=100时下b-h的曲线Fig.2 b-h curveswhen L=100

由图2可以看出：反射系数k为定值且大于零时，b随土壤厚度h的增大而增大，当h达到一定值时（约为9 m）时b达到最大值，然后随h的增大而减小；反射系数k为定值且小于零时，b随土壤厚度h的增大而减小，当h达到一定值时（约为7 m）时b达到最大值，然后随h的增大而减小；当反射系数趋近于零时，最优b值受上层土壤厚度h的影响越小。

2.2 反射系数

由图3最优b值与双层土壤的反射系数关系图可以看出：当上层土壤厚度h一定时，b值随k的增大而减小，即土壤上层厚度为定值时，下层土壤电阻率越大；接地网水平接地体当k为负数时总比k为正数时均匀，即下层土壤电阻率小于上层土壤电阻率时的水平接地体布置比下层土壤电阻率大于上层土壤电阻率时的水平接地体布置均匀。

图3 L=100 m时b和k曲线Fig.3 b-k curveswhen L=100 m

2.3 接地网面积

反射系数时，最优b值与接地网边长L的关系如图4所示。

图4 k=-0.3时的b-L曲线Fig.4 b-L curveswhen k=-0.3

由图4中可以看出，上层土壤厚度在大于10 m和小于10 m的时候b-L曲线呈现不同变化趋势。

当上层土壤厚度小于10 m时，随着边长的增大，b的值随之减小，当边长增大到180 m时，最优b值趋于稳定；当上层土壤厚度大于10 m时，随着边长的增大，最优b值随之减小，当增大到180 m时，最优b值随之稳定。

根据上述结果，在拟合最优b值的公式时应当分为h＜10 m和h≥10 m两种情况讨论。

2.4 计算最优b值的拟合公式

由于优化参数和土壤厚度，反射系数和接地网面积有关，所以利用神经网络拟合方法，将三个参数设为自变量，将每个数据看成一个三维坐标点，设函数为 b=f（h，k，L）进行拟合，以确定最优值。得到：

针对不同接地网土壤厚度边长对应的各系数如表2所示。

表2 拟合公式中的系数取值Tab.2 Coefficient values of fitting formula

2.5 优化效果校验

以一个尺寸为100 m×100 m的接地网为例，采用封闭型接地网，中间铺设水平垂直各七根均压带，整体埋深0.5 m，接地体半径为0.08 m，电导率为S/m，上层土壤电阻率为185.714Ωm，厚度为2 m，下层土壤电阻率为100Ωm，入地电流为1 kA。分别利用最优压缩比优化方法（方法一）和拟合函数法（方法二）进行布置。

从图5中可以看出，虽然利用函数方法使边缘网孔的接触电压值升高，但是降低了中心网孔的接触电压值，从而极大的降低了接触电压的峰值。并且从图中可以看出各个网孔的接触电压峰值和增减趋势更一致，使地表的接触电压分布更均匀。

图5 非均匀土壤下拟合函数与最优压缩比布置方法对角线接触电压分布Fig.5 Touch voltage distribution on diagonal of fitting function and optimal compression ratio in non-uniform area

3 优化公式在矩形接地网中的应用

3.1 长方形接地网各边分段数确定

长为100 m宽为60 m的矩形接地网，均压带布置由上述拟合公式确定，长边的分段数固定为8，宽边的分段数从1开始增加到8，得到结果如表3所示。

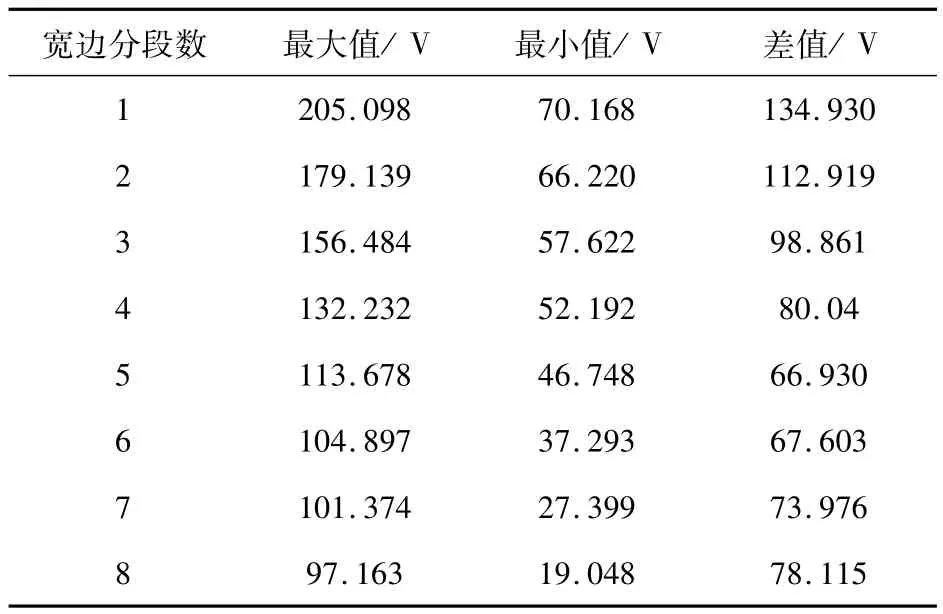
表3 矩形宽长度不同时的接触电压Tab.3 Max value，min value and D-value in rectangle

当每个网孔的最大接触电压最大值和最小值相差最小时，既是优化效果最好时。从表中可以看出，当宽边分段数为5时最大值与最小值的差值最小。当改变接地网宽度时，结果如表4所示，即横纵比与分段数之比接近时，优化效果最好。

表4 矩形宽不同时最佳分段数Tab.4 Divided method of width in different rectangles

3.2 应用效果检验

以一个尺寸为长为120 m，宽为80 m的矩形接地网为例，采用封闭型接地网，中间铺设水平五根，竖直八根均压带，土壤条件与2.5节中一致。

由于没有针对非均匀土壤环境下的矩形接地网优化方法，所以按照通用的指数分布优化接地网作为比较对象。分别按照最优压缩比方法（方法一）与拟合函数方法（方法二）的接地网布置方式如图6所示。

图6 拟合函数和最优压缩比布置接地网Fig.6 Grounding grid with fitting function and optimal compression ratio

由图6可以看出，相较于方法一，方法二布置的接地网减小了边缘网孔的尺寸，增大了中心网孔的尺寸。两种布置方法对角线接触电压分布计算结果如图7所示。

经过拟合，利用最优压缩比布置接地网的最大接触电压为155 V，利用拟合公式布置接地网的最大接触电压为138 V，降低了12.1%。由图8及图9可得两种方法全站接触电压分布图，拟合公式方法布置接地网全站接触电压整体效果优于最优压缩比方法。

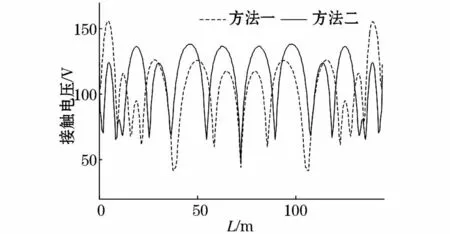
图7 均匀土壤下拟合函数与最优压缩比布置方法对角线接触电压分布Fig.7 Touch voltage distribution on diagonal of fitting function and optimal compression ratio in non-uniform area

图8 拟合公式方法布置接地网全站接触电压Fig.8 Distribution of touch voltage in method of fitting function

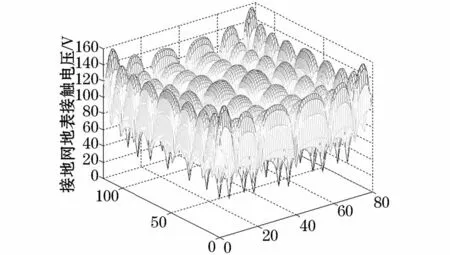
图9 最优压缩比方法布置接地网全站接触电压Fig.9 Distribution of touch voltage in methods of optimal compression ratio

4 结束语

本文通过分析接地网导体的不同布置方案，分析导体间距的变化与接触电压的影响，得出导体间距满足一定的曲线规律，通过推导得出此拟合函数，计算结果表明：

（1）对于双层土壤，针对不同的反射系数k，上层土壤厚度h，接地网面积L，分析得到接地网最优布置的计算公式；

（2）在矩形接地网中，经实验仿真发现当平行于长和宽的水平接地体数量之比接近与长宽的长度之比时，优化效果最好；

（3）研究得出在非均匀土壤环境下，针对矩形接地网，此公式同样适用，最大接触电压降低12%左右。