燃料电池系统宽范围输入电压变换器设计

吕耀文，赵耀

（1.包头职业技术学院，内蒙古包头014030；2.内蒙古电力勘测设计院有限责任公司，呼和浩特010020）

0 引 言

近年来新能源被广泛运用，其中氢能以其清洁性、高效性和资源充足性，成为了符合要求的新能源之一，而燃料电池是其最佳应用平台。因此，世界各国越来越重视燃料电池供电系统的研究。

燃料电池供电系统的通用结构由燃料电池、单向DC-DC变换器、负载端变换器和储能装置及其相应的双向DC-DC变换器组成。其最核心的部分是单向DC/DC变换器模块，但由于燃料电池的输出特性较软，易受负载的影响使其输出电压变化范围较大（一般在200 V～400 V之间），因此单向DC/DC变换器面临宽范围输入电压问题。传统的单向DC/DC变换器主要有Buck、Boost、Flyback、单管正激以及双管正激变换器等，其中传统的Buck/Boost变换器在面对宽范围输入电压时其使用受到很大地限制；而传统的单管Buck-Boost变换器可升压降压特性使其在面对宽范围输入电压时虽具有较强的适用性，但由于其开关管电压应力过高不适合在大功率场合的应用［1］。类似地，宽范围输入电压使得Flyback变换器具有同样地问题，并且其输出电压还存在尖峰，不适用于对输出电压质量要求较高的场合。单管正激变换器以及双管正激变换器对于宽范围输入电压的适应性则比上述变换器更差［2-3］。因此，目前大多数燃料电池供电系统的单向DC/DC变换器采用全桥变换器结构，该结构具有开关管电压应力低、软开关技术应用成熟等优点，在大功率场合得到广泛应用，但其在宽范围输入电压场合的优势不明显，且对于宽范围输入电压造成的器件应力变化和电路环流亦没有较好的解决方法。此外，该结构所使用开关器件过多，因而整体变换器体积也较大。

目前已有不少文献对宽范围输入电压变换器进行了较为深入的研究。文献［4］提出了一种全桥组合式直流变换器以用于较宽输入电压范围场合，但由于其采用了多个变压器使得变换器体积偏大且其功率密度较低。同时，其控制策略也较为复杂［5-8］不利于工程实际应用。此外，为了满足煤矿井下设备对开关电源的特殊要求，文献［9］所提设计方案将普通开关电源和自适应交流调压电源相结合，使得所设计电源具有较强的耐电压、电流冲击能力并且不产生热污染，但该开关电源直接与85V～825V交流电压相连接，当传输较大功率时其变压器体积必须设计得很大［10］。还有文献对PFC电路（即由单管Buck电路和单管Boost电路级联组合而成，以下简称双管Buck-Boost变换器）进行了研究，表明该变换器在宽范围输入电压场合中有较好的适用性［11］，能够根据输入电压的大小自动切换电路工作模式，其电路结构简单，使用器件较少，因此变换器体积小，功率密度高。此外该电路能有效解决传统单管Buck-Boost电路开关管电压应力过高的问题，减小了变换器开关损耗并提高了其效率，但该文献仅从宽范围输入电压时双管Buck-Boost变换器的适用性角度进行了研究，并未从整个系统的控制角度进行分析，无法为后级变换器提高稳定电压。

结合双管Buck-Boost级联电路在宽范围输入电压场合良好的适用性以及诸多的优点，本文对其设计了基于平均电流控制的电压、电流双闭环控制环路，在该控制方式下双管Buck-Boost级联电路能够在宽范围输入电压下获得稳定的输出电压，从而降低了燃料电池系统后级变换器设计和优化的难度。此外，针对双管Buck-Boost变换器在升、降压两种工作模式的切换点振荡问题提出了一种简单有效的解决方案。最后，通过PSIM仿真软件平台下的仿真分析以及小功率实验样机的实验研究验证了所提采用双闭环控制环路双管Buck-Boost变换器在宽范围输入电压场合的优越性能。

1 双管Buck-Boost变换器的工作原理

图1为双管Buck-Boost变换器的拓扑结构图，它有三种工作模式：Buck工作模式、Boost工作模式和临界工作模式。通过对输入、输出电压关系的判断即可决定电路工作模式，任一时刻仅有一个开关管动作，整个电路始终工作于单管动作状态。

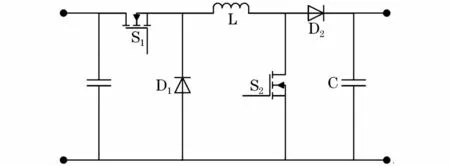
图1 双管Buck-Boost变换器拓扑结构Fig.1 Topological graph of dual switch Buck-Boost converter

第一种工作模式为Buck电路模式如图2（a）所示，此时该变换器的输出电压小于其输入电压，电路降压由S1控制开关管的通断实现并且S2开关管被控制为一直关断状态；第二种工作模式为Boost电路模式如为图2（b），此时该变换器的输出电压大于输入电压，电路升压由S2控制开关管的通断实现并且S1开关管被控制为一直导通状态。此外，第三种工作模式为Buck电路和Boost电路的临界状态，即通过以上两种变换器工作模式的互补运行实现将宽范围的输入电压转换成稳定的输出电压，此时S1开关管被控制为常导通状态而S2开关管被控制为常关断状态，能量通过电感L直接传递到输出侧，其等效电路如图2（c）所示。

2 控制环路设计以及切换点振荡抑制方法

为避免双管Buck-Boost变换器采用单电压环控制导致较大幅度的系统输出电压波动，甚至造成系统不稳定运行，本文基于平均电流控制策略设计了电压、电流双闭环控制环路，以期实现双管Buck-Boost变换器在宽范围输入电压下获得稳定的输出电压。平均电流控制通过引入电感电流来构建电流内环，通过电流内环更快的反映输入电压的波动，使得系统在遇到输入电压波动时能迅速自调节恢复至稳态［12］。控制环路设计时采用直接串联电阻方法对电感电流进行采样以得到反映电感电流的电压信号VRs，VRs与电压外环输出的输出电压误差信号进行比较产生电流内环输出信号VCA，整个控制系统拓扑结构以及系统设计参数详见图3以及表1。

图2 双管BuckBoost电路三种工作模式等效电路Fig.2 Three workingmodes equivalent circuits of dual switch Buck-Boost circuit

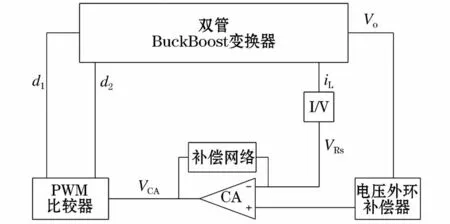
图3 工作模式切换的平均电流控制环路原理图Fig.3 Schematic diagram of average current control with the automatic variation of workingmodes

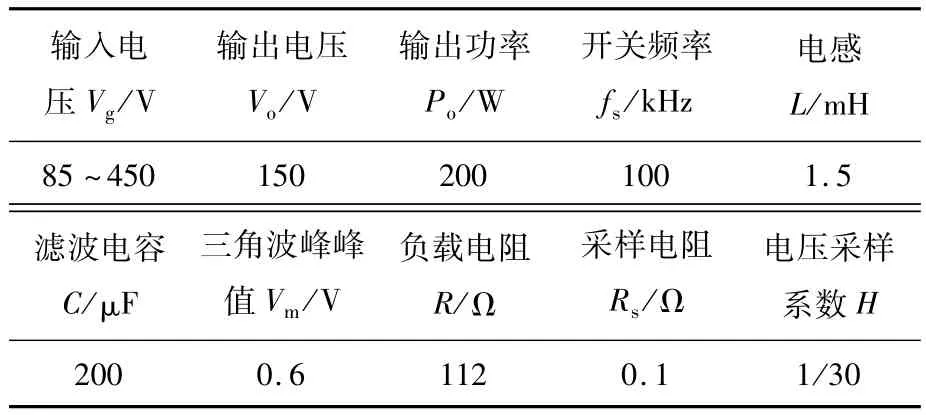
表1 系统设计参数Tab.1 System design parameters

2.1 电流环设计

本文采用单零点-单极点补偿网络来设计电路的电流控制环，补偿网络结构如图4所示。当输入电压为150 V时变换器电路工作于Buck、Boost模式切换的临界状态，即其输入电压和输出电压相等。此外，在该输入电压下基于Buck变换器电路模型的电流内环补偿网络也同样适用于其他输入电压。

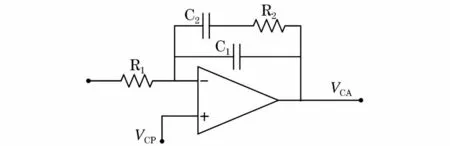
图4 单零点单极点补偿器Fig.4 Single-zero single-pole compensator

可得基于Buck变换器电流补偿网络输出到电流采样电阻Rs两端电压的传递函数为［12］：

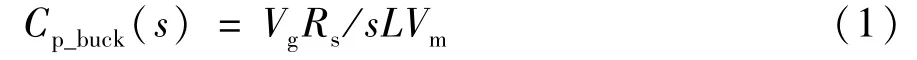
本文所设计的电流补偿器相关参数如表2所示。

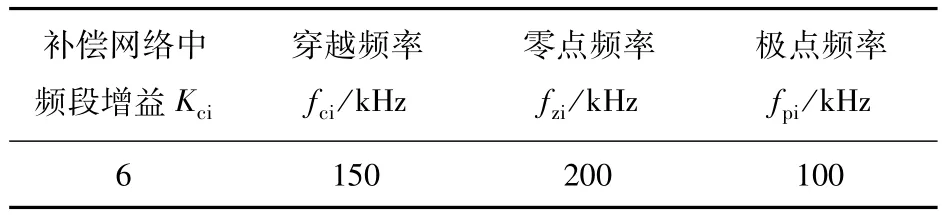
表2 电流补偿器设计参数Tab.2 Design parameters of current compensator

最终可得所设计的单零极点电流内环补偿器如式（2），且其幅相特性如图5所示。

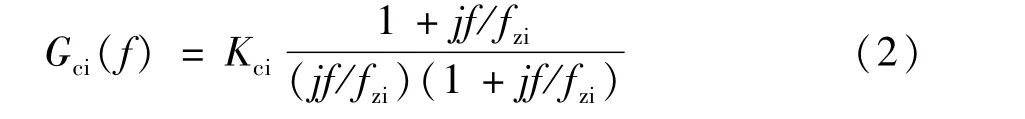
补偿后Buck变换器的开环传递函数为：

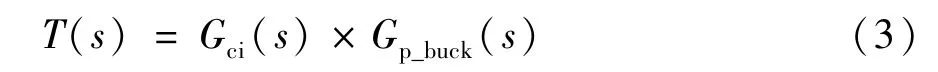
图6为其开环传递函数的幅频、相频特性。由该图不难看出，该系统具有下降频率为-40 dB/dec的高频段从而实现了其迅速衰减，同时具有-20 dB/dec穿越0 dB线的中频段，其相角裕量约为55.3°且截止频率为17 kHz。综上所述本文所设计的电流补偿器达到了预期补偿效果。

2.2 宽范围输入电压下电流控制器适用性验证

上节在输入电压Vg=150 V条件下以Buck电路为模型设计了电流内环补偿器，但是还需进一步验证在高于150 V时的Buck电路和低于150 V时的Boost电路下该电流补偿器是否适用。因此，本节将进行深入分析和验证在85 V～450 V的输入电压范围下该电流补偿器的适用性。

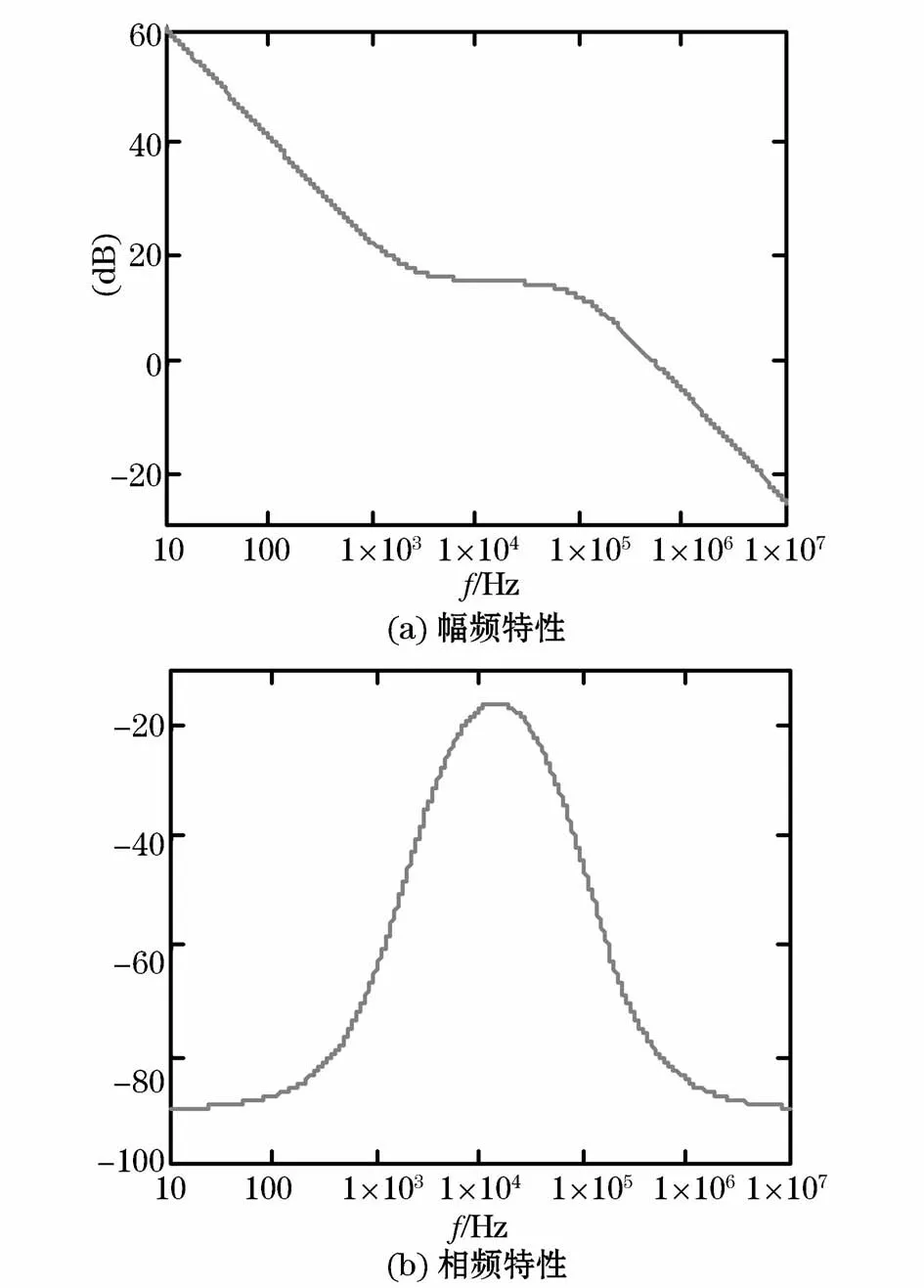
图5 电流补偿器的幅相特性Fig.5 Frequency characteristics of current compensator

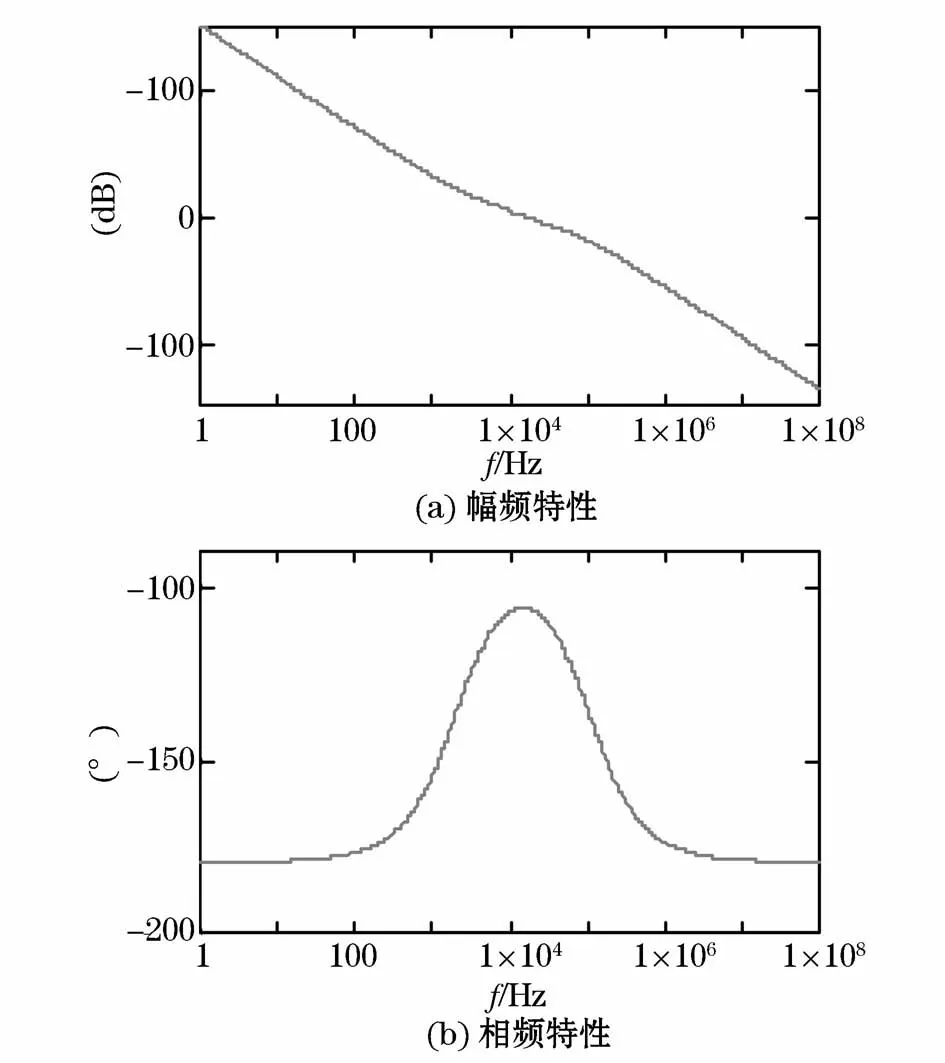
图6 补偿后Buck变换器开环传递函数幅相特性Fig.6 Frequency characteristics of open-loop transfer function in Buck converter after compensation

8个输入电压值Vg1～Vg8分别为85 V、100 V、150 V、200 V、250 V、350 V、400 V和 450 V，并且对这8个不同的输入电压均采用第2.1节所设计电流内环补偿器进行补偿，则补偿后电流控制系统的开环传递函数为：

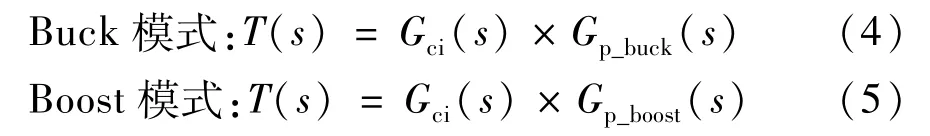
式中Gp_boost（s）为Boost变换器电流内环控制对象的传递函数，其表达式为：

输入电压为Vg1～Vg3时电路工作于Boost模式，输入电压为Vg4～Vg8时电路工作于Buck模式。图7为所设计的含有电流补偿器的电流控制系统在这8个不同输入电压下的开环幅相特性。从图7不难看出，不同输入电压下经电流补偿网络补偿后的电路具有为一簇相互平行曲线的幅频特性，该幅频特性具有可迅速衰减的下降率为-40 dB/dec的高频段，并且其中频段还以-20 dB/dec穿越0 dB线，而如图8所示其相频特性曲线几乎是重合的。

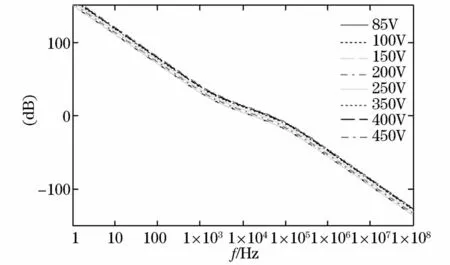
图7 补偿后的电路的开环传递函数幅频特性Fig.7 Amplitude-frequency characteristics of circuit open-loop transfer function after compensation

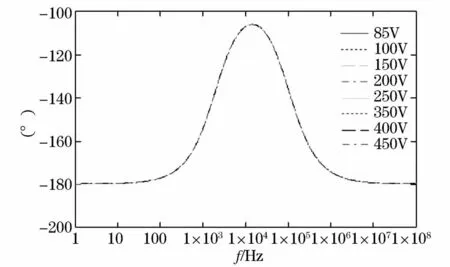
图8 补偿后电路开环传递函数的相频特性Fig.8 Frequency characteristics of compensating circuit open loop transfer function

通过电流补偿网络补偿后的电路开环传递函数的幅频特性在不同输入电压下的穿越频率以及相位裕量对比详见表3。由表3可知所设计的电流补偿网络在85 V～450 V的输入电压范围内是合理的，能够使系统获得良好的高频抗干扰能力和动静态特性。

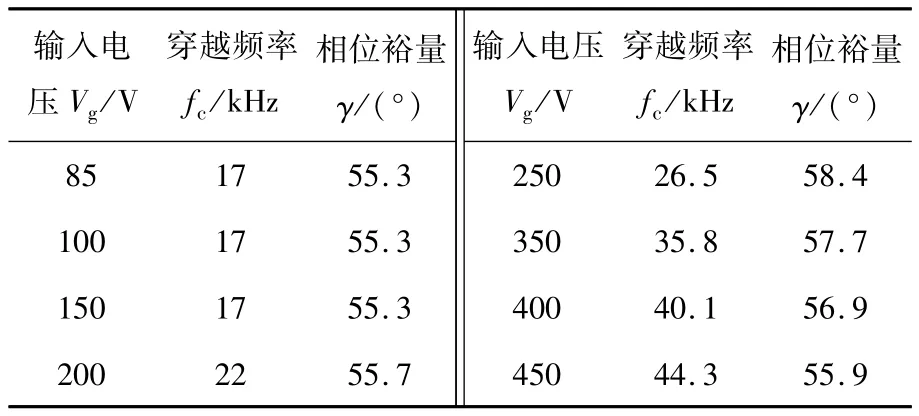
表3 不同输入电压下系统开环参数对比Tab.3 comparisons of system open-loop parameters with different input voltage

2.3 电压外环设计

本节将2.1节和2.2节所设计的电流控制内环视为控制对象的一个环节，从而对电压外环控制器进行设计。图9为等效单电压外环控制系统框图，其中Ap（s）为等效功率级传递函数以及 Gcv（s）为电压补偿网络传递函数。

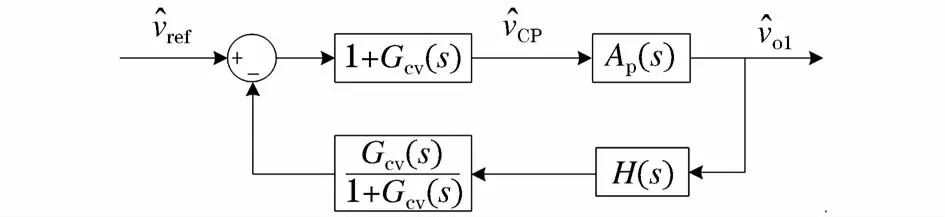
图9 等效单电压环控制系统框图Fig.9 Block diagram of equivalent single voltage loop control system

图10为由电流控制环及负载组成的等效功率级图。其中，电压控制器的输出电压是该等效功率级的输入信号，变换器的输出电压是该等效功率级的输出信号，而Z（s）为电流控制环的负载等效阻抗以及Aif（s）为电流控制环的闭环传递函数。

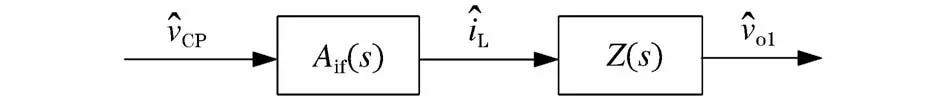
图10 等效功率级图Fig.10 Diagram of equivalent power stage

图11为由输出电容和负载电阻组成的Buck、Boost变换器的电流内环负载等效阻抗。由于燃料电池中铝电解电容的等效串联电阻Resr与电容值C的乘积近似为常数50×10-6～80×10-6。因此在本文设定其乘积为50×10-6且所设定的电容C为200μF的条件下可计算出Resr为0.25Ω。

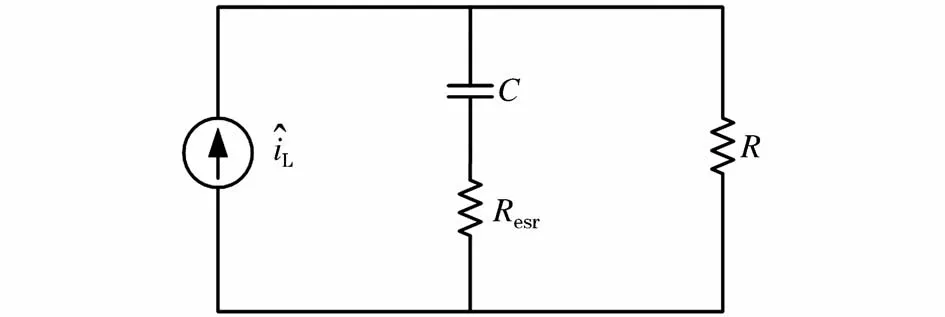
图11 电流控制环的负载等效阻抗Fig.11 Equivalent load impedance of current control loop

则所设计的电流控制环的负载等效阻抗为：

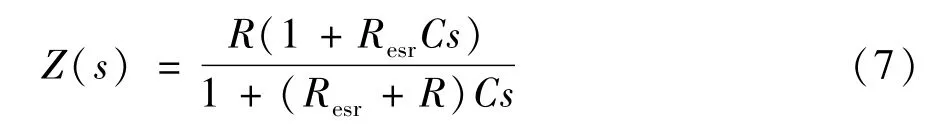
则负载等效阻抗的零点和极点频率分别为：

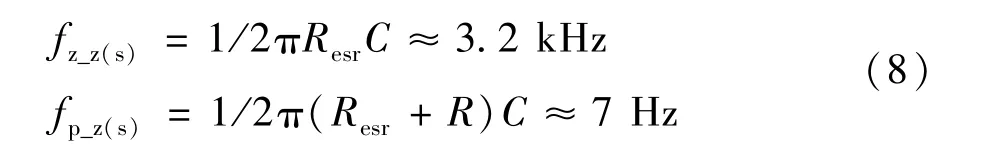
电流控制环的闭环传递函数Aif（s）可用双极点模型近似逼近：

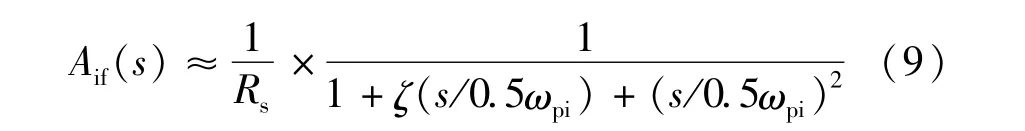
式（9）中ωpi为电流控制环极点角频率，ζ为电流控制环的阻尼比，其取值范围为1～1.5。取ζ=1时，等效功率级传递函数为：

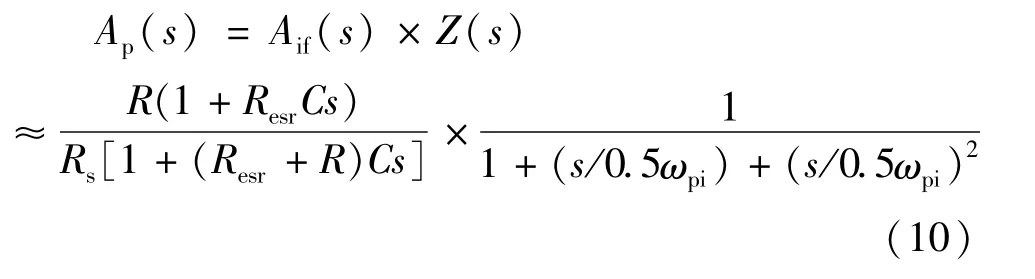
由式（10）可知电压控制系统需要增加两个零点才能抵消具有一个零点和三个极点的等效功率级的全部极点，因此本文的电压外环控制器采用双零点-双极点补偿网络。由上式计算可知fpv1=fz_z（s）=3.2 kHz，因此将第一个零点fzv1设置于负载极点附近从而使其抵消等效功率级的ESR零点；同理可计算出fpv2=fs=100 kHz，因此将第二个零点fzv2设置于开关频率附近以减小电流环的极点fzv2=fpi/2=50 kHz对系统的影响。考虑到所连燃料电池系统后级变换器的负载特性，本文将截止频率设定为fcv=fs/4=4kHz作为截止频率，此时可得到Kcv=15的补偿网络增益。综上所述所设计的电压补偿网络如式（11）为：

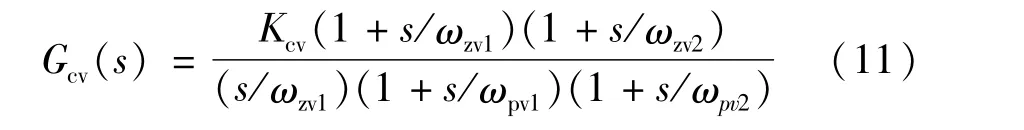
可得补偿后变换器电路的开环传递函数为：

图12为补偿后系统的传递函数幅相特性曲线。由图可知，该传递函数高频段幅频特性具有-40 dB/dec的下降斜率，这说明系统具有较强的抗干扰能力；而中频段幅频特性具有-20 dB/dec的下降斜率，这说明系统有足够的相位裕度；同时其低频段幅频特性具有-20 dB/dec的下降斜率，这说明系统的稳态误差等于零，因此该传递函数的幅频特性分析可以证明所涉及的电压控制环是稳定的。

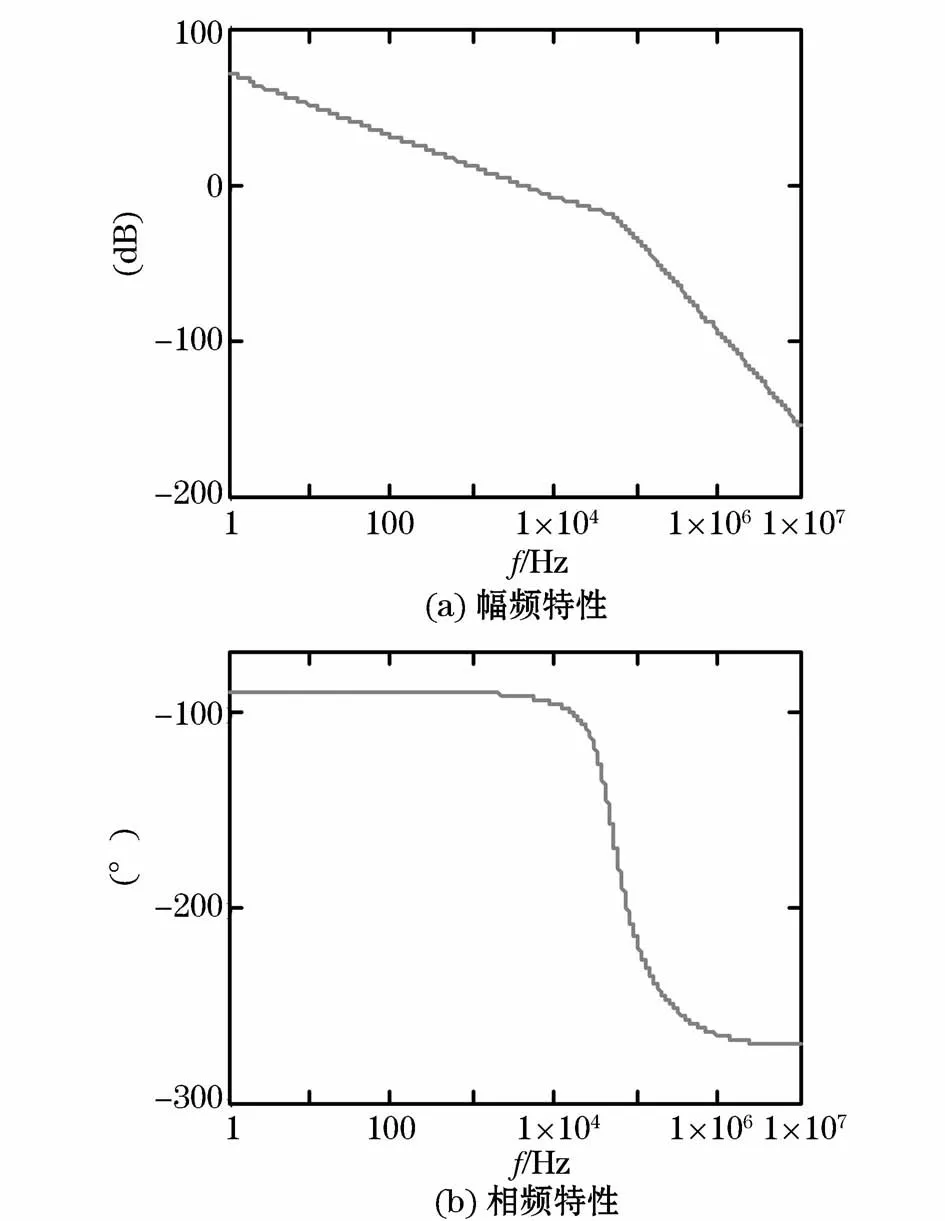
图12 补偿后的系统传递函数幅相特性Fig.12 Frequency characteristics of system transfer function after compensation

2.4 切换点振荡的抑制方法

本文通过控制两路峰峰值相同但幅值不同的同频率三角波产生两个不同的PWM开关信号，从而实现双管BuckBoost变换器在Buck、Boost两种工作模式之间的自动切换，如图13所示。

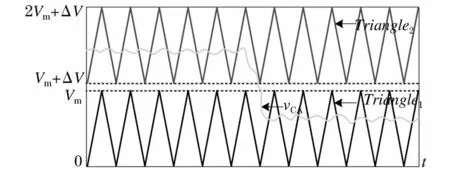
图13 工作模式自动切换原理图Fig.13 Schematic diagram of automatic variations ofworkingmodes

Triangle2与Triangle1的三角波的峰峰值和频率均相等，但 Triangle2幅值比 Triangle1大 Vm。通过Triangle1和Triangle2的三角波信号与电流环CA的输出信号VCA的交截状态进行判断并对变换器的工作模式进行自动切换：当处于VCA大于Vm的运行状态时由于VCA始终比三角波Triangle1大，这使得S1开关管将控制为一直导通，同时S2开关管的通断由Triangle2的三角波信号与VCA比较所产生的占空比信号来控制，此时所设计的变换器电路工作于Boost模式；当处于vCA小于Vm的运行状态时，同理，由于VCA始终比三角波Triangle2小，这使得S2开关管将控制为一直关断，同时S1开关管的通断由Triangle1的三角波信号与VCA比较所产生的占空比信号来控制，此时所设计的变换器电路工作于Buck模式。

值得注意的是，在两种工作模式切换点附近，当VCA信号出现小信号扰动时会使电路在切换点附近产生振荡，使得电路在Buck、Boost两种工作模式之间来回不停切换，从而影响电路的正常工作。为抑制切换点振荡，可将三角波Triangle2上移了一个ΔV的偏置，即扩大临界工作状态的范围，以牺牲输出电压纹波的代价来抑制变换器在切换点附近的振荡。

3 仿真分析

为验证所提采用基于平均电流控制的电压、电流双闭环控制环路的双管Buck-Boost变换器在宽范围输入电压场合的性能，在PSIM仿真软件中建立了仿真模型，系统仿真参数如表4所示。

表4 仿真参数Tab.4 Simulation parameters

仿真时设定输入电压起始值为85 V，在0.05 s时刻跳跃到450 V，仿真时间0.1 s。从图14可知，在输入电压阶跃时，电感电流出现了约为3 A的电流尖峰后迅速到达下一个稳态，而输出电压出现约为2.5 V的扰动尖峰后迅速自调节恢复至150 V，系统的输出电压具有良好的抗输入电压扰动特性。

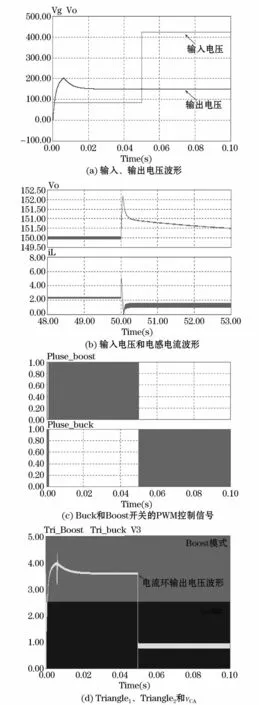
图14 仿真结果Fig.14 Simulation results

4 实验验证

由于实验室设备条件有限，仅在实验室搭建了小功率实验样机对上述理论分析以及所提方案进行实验验证。其中，由自藕调压器经三相整流桥整流后提供实验样机的电源输入电压，同时由20Ω的水泥电阻作为负载，并且，实验验证中通过调节自藕调压器以使输入电压在较宽范围内发生改变，从而实现对宽范围输入电压的模拟。

实验所得Buck、Boost两种工作模式下的PWM比较器所输出的PWM信号如图15（a）、（b）所示，所得实验结果与理论分析完全一致。实验所得输入、输出电压波形如图15（c）所示，当输入电压不断变化时，示波器所测得输出电压的峰峰值约为300 mV并且纹波较小，而其平均值约为15.4 V，因此该实验结果证明了所设计的变换器可在输入电压变化时维持其输出电压基本恒定不变。通过小功率原理样机的实验，验证了双管Buck-Boost变换器的双闭环控制环路设计的正确性。

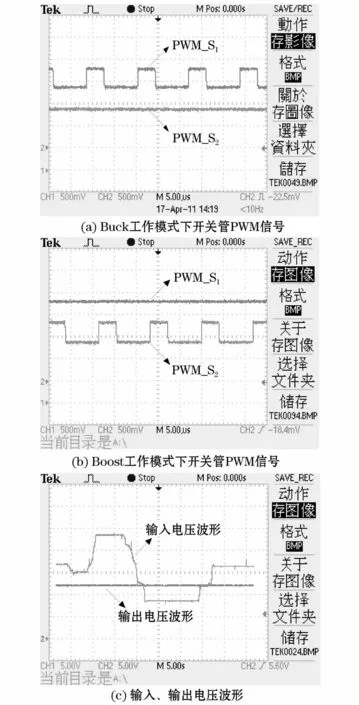
图15 实验结果Fig.15 Experiment results

5 结束语

针对双管Buck-Boost级联电路在宽范围输入电压场合良好的适用性以及诸多的优点，本文对其设计了基于平均电流控制的电压、电流双闭环控制环路，该控制方案可为该级联电路在燃料电池中的应用奠定一定的理论基础。主要有以下结论：

（1）采用基于平均电流控制的电压、电流双闭环控制环路的双管Buck-Boost级联电路能够在宽范围输入电压下获得低纹波、高稳定性的输出电压，可降低燃料电池系统后级变换器因输入电压不稳定而带来设计和优化的难度，并能有效提高整个燃料电池系统的供电稳定性；

（2）针对双管Buck-Boost变换器在升、降压两种工作模式的切换点振荡问题提出了一种简单有效的解决方案，该方案以牺牲输出电压纹波的代价来抑制变换器在切换点附近的振荡，可有效改善电路在切换点的工作性能。