基于模糊神经网络的光伏发电系统功率控制方法

陆畅，智勇军，周志锋

（国网河南省电力公司平顶山供电公司，河南平顶山467001）

0 引 言

大量光伏发电系统接入电网，由于电网故障而快速将光伏发电系统切出电网的方法目前已不能满足要求，突然将大容量光伏切出系统会对电网系统造成严重冲击，甚至导致电网崩溃［1-4］。为了保证光伏发电系统在故障时不脱离电网，需要光伏发电系统具有低电压穿越（Low Voltage Ride-Through，LVRT）能力［5-6］。电网电压正常运行状况下，光伏并网逆变器通常采用传统电压/电流双闭环控制策略实现光伏发电系统并网运行。当电网电压发生三相对称跌落时，采用传统的双环控制和 LVRT控制策略相互切换来实现光伏发电系统的低电压穿越的控制目标［7-8］。

由于电网电压对称跌落不含负序分量，只需抑制并网逆变器出口电流，防止过流保护动作，实现其在电网电压对称跌落时的低电压穿越［9-10］。然而，在电网实际运行中，绝大多数故障为不对称故障，包括单相接地、两相接地故障等，若采用传统三相电压对称的低电压穿越控制策略，由于负序电流存在，并网逆变器的并网功率与光伏阵列发出功率不平衡，并网逆变器直流侧电压降大幅度波动，影响光伏发电系统的稳定运行，甚至导致其脱网，将不能满足国标和电网公司关于入网标准的要求［11-13］。

将模糊神经网络用于光伏发电系统功率控制的应用场合，在电网电压突变和跌落情况下能够快速地调整系统的工作模式，以适应光伏阵列最大输出功率和并网逆变器额定容量及最大输出电流的限制，具有稳定性强、跟踪速度快等优点。阐述了电网故障控制器运行模式切换策略，建立了模糊神经网络算法的模型，并在Matlab/Simulink平台下搭建了系统仿真模型，仿真结果验证了所提出控制策略的有效性和可行性。

1 光伏发电系统的拓扑结构

如图1所示，并网光伏发电系统的主电路包括光伏阵列、Boost升压斩波电路、三相逆变器、并网电抗器L、并网开关SSR、并网变压器和三相电网，光伏阵列依次通过Boost升压斩波电路、三相逆变器、并网电抗器L、并网开关SSR和并网变压器接入三相电网；CPV为光伏阵列输出端口并联电容，同时为Boost升压斩波电路提供输入电压；VPV和IPV分别为光伏阵列的输出电压与输出电流；直流电容Cdc接在Boost升压斩波电路输出端，Cdc同时作为三相逆变器的直流母线电容，其工作电压为Vdc；三相逆变器通过并网电抗器L、并网开关SSR和并网变压器接入三相交流电网。

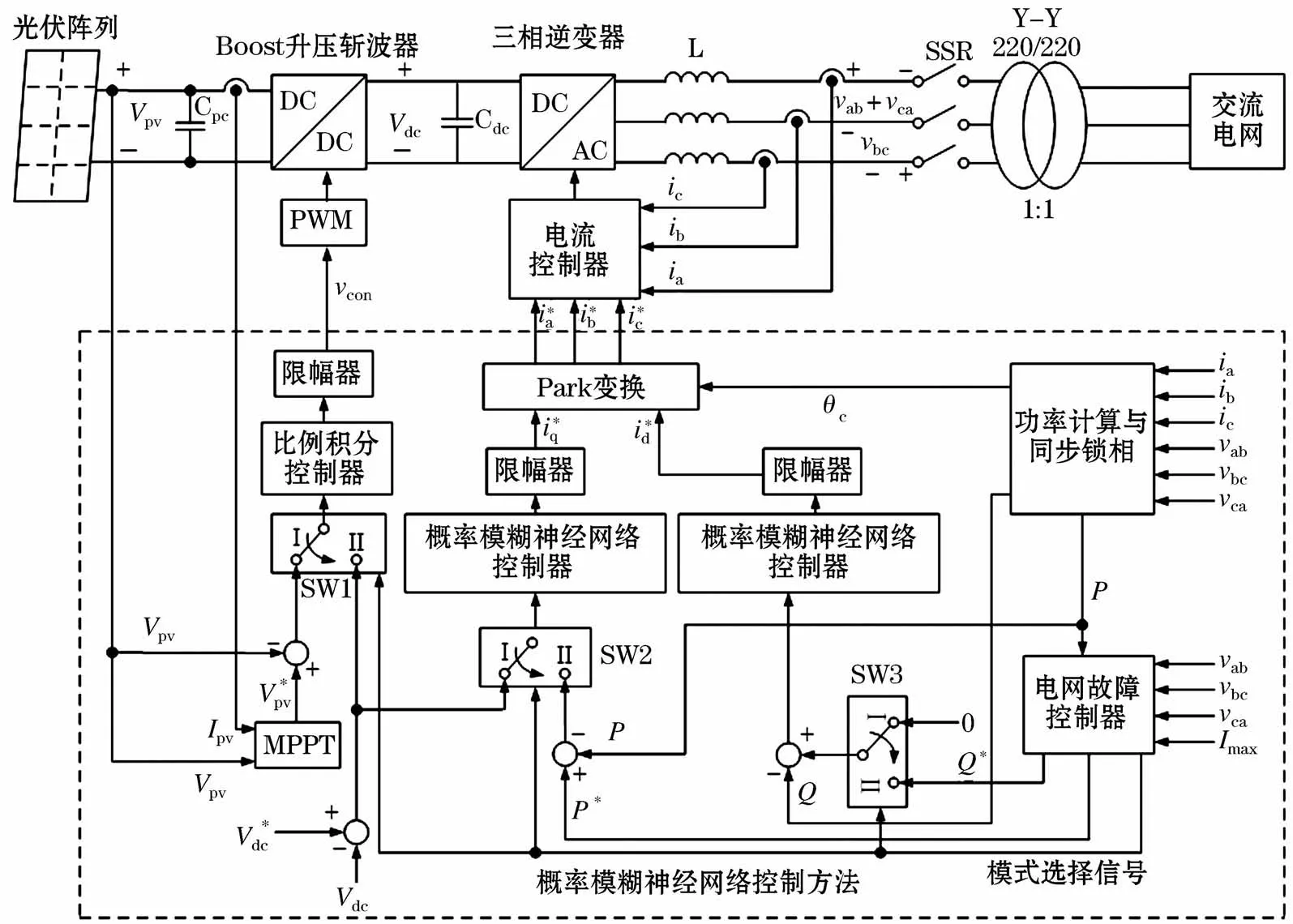
图1 光伏发电系统电路拓扑及其控制框图Fig.1 Circuit topology and its control block diagram of PV generation system

2 光伏发电系统的控制策略

2.1 有功功率和无功功率参考值计算

如图1所示，三相逆变器交流输出相电压和线电压的关系表示为：

式中 ［vab，vbc，vca］T为三相逆变器交流输出线电压，［va，vb，vc］T为三相逆变器交流输出相电压。对式（1）采用Clark变换，可得：

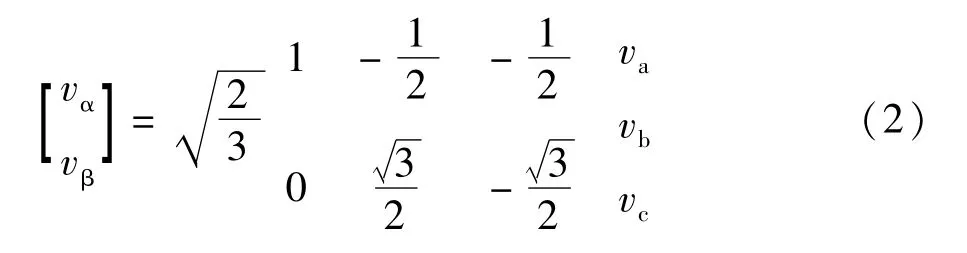
式中vα和vβ分别为三相逆变器输出电压在静止αβ坐标系统下α轴和β轴的分量。采用Park变换，将静止αβ坐标系统的输出电压［vα，vβ］T转换到同步旋转坐标系统，表示为：

式中vd和vq分别为三相逆变器输出电压在dq同步坐标系统下d轴和q轴的分量。采用Park变换，将三相逆变器输出电流［ia，ib，ic］T转换到dq同步坐标系统，表示为：

式中id和iq分别为dq同步坐标系统下d轴和q轴电网电流分量，iq分量用来控制光伏发电系统向电网注入的有功分量，id分量用来控制光伏发电系统向电网注入的无功分量。光伏发电系统向电网注入的瞬时有功功率P和瞬时无功功率Q分别表示为：

通过同步锁相（PLL）后，三相逆变器输出电压相量与电网电压相量同相位，即vd=0，则瞬时有功功率和瞬时无功功率分别表示为：

设Vsag表示电网电压跌落幅度的标幺值，其范围为［0，1］，则光伏发电系统需要注入电网的无功电流参考值表示为：

式中 Vbase为电压基值，当Vsag大于0.1 pu时，光伏发电系统对电网的无功功率支撑控制模式启动。为了满足光伏逆变器低电压穿越（LVRT）的要求，以及避免逆变器输出电流超过装置额定电流导致元器件损坏，三相逆变器视在功率最大值表示为：

式中Imax表示光伏发电系统注入电网电流的最大允许值。因此，有功功率和无功功率的最大允许值分别表示为：

上述有功功率和无功功率最大允许值P*、Q*将作为光伏发电系统向电网注入有功功率和无功功率的参考值，与光伏发电系统实际有功功率和无功功率P、Q分别求取偏差后，作为模糊神经网络控制器的输入信号。

2.2 电网故障控制器的模式选择方法

在上述分析基础上，建立光伏发电系统的电网故障控制器模型，根据有功功率、无功功率和三相逆变器电流的最大允许值，建立双模式切换控制策略，动态地调整Boost升压斩波电路的工作模式和三相逆变器的概率模糊神经网络控制输入参考信号。电网故障情况下，光伏发电系统的双模式切换的控制策略如下：

模式I：当P*大于光伏阵列的有功功率率PPV时，通过控制三相逆变器的直流母线电压，将光伏阵列的有功功率率PPV全部注入电网；三相逆变器电流可控制在Imax以内，Boost升压斩波电路工作在最大功率点跟踪模式（MPPT模式）；

模式II：当P*小于或等于光伏阵列的有功功率率PPV时，Boost升压斩波电路暂停最大功率点跟踪，并开始跟踪功率P*；Boost升压斩波电路与三相逆变器之间的功率不均衡问题通过控制三相逆变器直流母线电压来解决。

电网故障控制器通过开关SW3（如图1所示）选择工作模式。如图2所示，双模式切换控制策略的具体操作流程包括以下步骤：

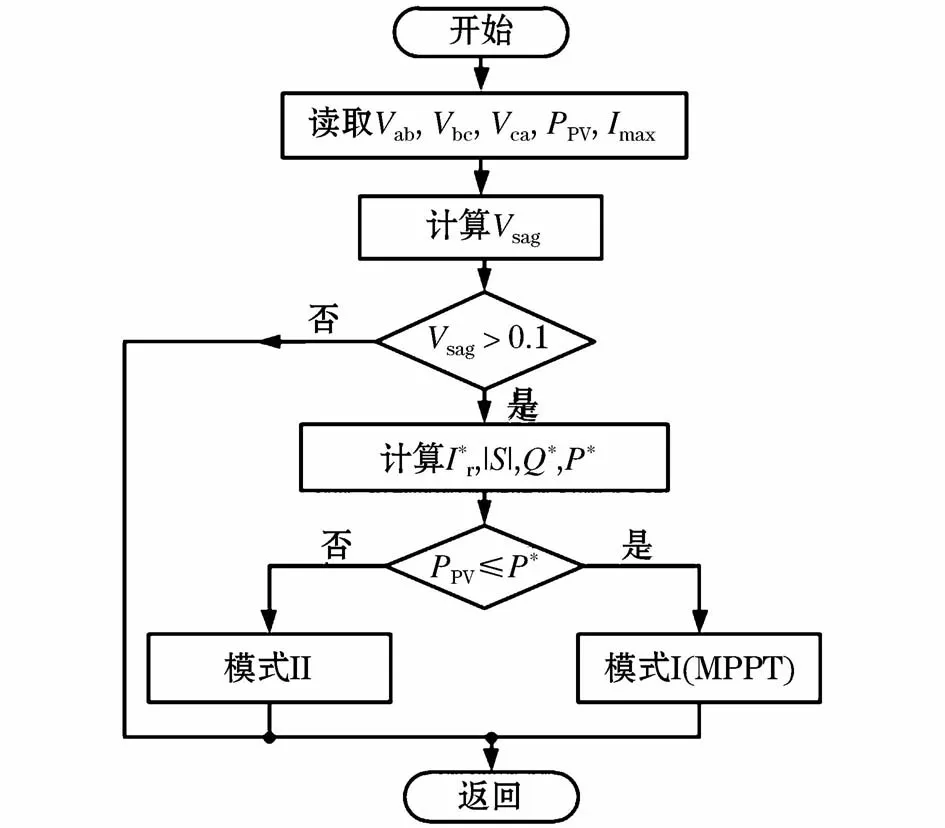
图2 光伏发电系统电网故障控制器的控制模式选择流程图Fig.2 Controlmode selection flow chart of grid fault controller in PV generation system

（1）读取三相逆变器交流输出线电压 vab，vbc，vca，光伏发电系统注入电网电流的最大允许值Imax，计算光伏阵列的有功功率率PPV，并计算Vsag；

（2）判断Vsag是否大于0.1，若是，光伏发电系统对电网的无功功率支撑控制模式启动，进行下一步，否则不操作；

（3）计算 Ir*，｜S｜，P*，Q*；

（4）判断PPV是否小于或等于P*，若是则进入模式I，否则进入模式II。

Boost升压斩波电路内环控制器采用比例积分控制器，比例积分控制器的输入信号通过开关SW1根据电网故障控制器的输出模式信号来选择输入信号，系统工作在模式 I时，将最大功率点跟踪模式（MPPT）下的输出信号VPV*与光伏阵列的实际输出信号VPV求偏差，将偏差信号作为Boost升压斩波电路内环控制的输入信号。

当系统工作在模式II时，将三相逆变器直流母线电压参考值Vdc*和实际值 Vdc求取偏差后作为Boost升压斩波电路内环控制的输入信号。Boost升压斩波电路内环控制器的输出信号与三角载波比较并形成Boost升压斩波电路开关器件的PWM脉冲控制信号。三相光伏逆变器内环电流控制器模型，采用比例积分控制，实现输出电流ia，ib，ic对参考信号的跟踪控制，将三相光伏逆变器内环电流控制器的输出信号与三角载波比较并形成三相逆变电路各开关器件PWM脉冲控制信号，从而实现光伏发电系统并网控制以及在电网故障情况下对电网动态无功功率支撑的目标。

3 模糊神经网络模型及算法流程

接下来建立概率模糊神经网络控制器，求取三相逆变器注入电网的有功和无功电流参考值。概率模糊神经网络控制器的计算流程如图3所示，概率模糊神经网络控制器包括6层网络结构：第1层为输入层、第2层为隶属度层、第3层为概率层、第4层为TSK模糊推理机制层、第5层为规则层、第6层为输出层；在隶属度层中，每个节点采用不对称高斯函数实现模糊化运算［14-15］。

图3 模糊神经网络控制器模型及算法流程Fig.3 Flow chart of themode of fuzzy neutral network controller and its algorithm

定义第j个模糊If-Then规则表示如下：

式中xi，i=1，2为概率模糊神经网络控制器的输入，M1j和M2j为模糊集，Tk为TSK模糊推理机制，cik为可调节的权系数；

第1层（输入层）：输入层的节点将输入变量xi，i=1，2，传递到第2层，输入层的节点输入信号和输出信号之间的关系如下：

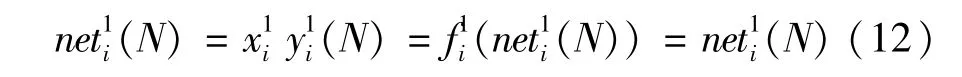
第2层（隶属度层）：本层每个节点采用不对称高斯函数实现模糊化运算，节点输入信号和输出信号之间的关系表示如下：

式中mj2为第i个输入变量第j项不对称高斯函数的均值和别为第i个输入变量第j项不对称高斯函数的左侧标准差和右侧标准差，yj2为第2层节点的输出变量；

第3层（概率层）：第3层的节点输入输出关系如下：

式中Pjp（N）对应于第j个输入变量第p个节点的输出信号，和分别对应于第j个输入变量第p个节点不对称高斯函数的均值和标准差；为了减小计算量，可以将和设置成常数，当p=1时，-1；当 p=2时，当 p=3时，

第4层（TSK模糊推理机制层）：本层中，输出信号为输入信号的线性组合，第k个节点的输出信号为［14］：

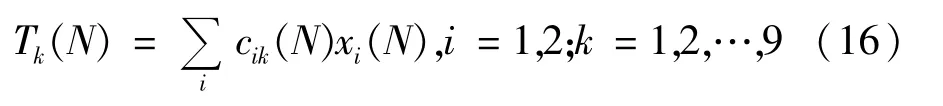
式中cik为可调节的权系数，xi为输入变量，N为迭代次数；

第5层（规则层）：本层第一部分为第2层和第3层节点输出信号yj2（N）和Pjp（N）的乘积，因此本层第一部分第k个节点的输出信号可表示为：

式中Sj（N）为第3层节点输出信号Pjp（N）的乘积，对应于第2层的第j个节点；

本层第二部分为第5层输出信号表达式，即为第一部分输出信号ykI（N）与第4层输出信号 Tk（N）的乘积，因此第k个节点的输出信号可表示为：

式中yko表示规则层第k个节点的输出信号；

第6层（输出层）：本层由一个节点O构成，计算所有上层节点输出信号的加权累加效应，其数学模型表示为：

式中wk6（N）表示第k个模糊化规则对第o个输出信号作用强度的权系数，yko（N）为第6层节点的第k个输入信号；yo6（N）=iq*为光伏逆变器注入的有功电流，yo6（N）=id*为光伏逆变器注入电网的无功电流。

在上述步骤基础上，建立概率模糊神经网络控制器的误差后向传播学习算法机制，构造一个梯度向量，使得其中每一个元素均为能量函数相对于算法参数的一阶微分，从而完成概率模糊神经网络的参数在线自整定。参数和初始值分别设置为0，1，1，1；参数初始值分别设置为 -1，0，1，-1，0，1；学习率 η1～η5初始值均为零［15］。

4 仿真与分析

4.1 模型

为了验证本文提出的基于模糊神经网络功率控制策略的有效性，在Matlab/Simulink平台搭建了如图1所示的并网型光伏发电系统仿真模型［14］。额定功率45 kW，额定电压有效值为220 V，逆变器直流母线电容电压为750 V，并网电感L=0.5mH，逆变器直流母线电容Cdc=1.2 mF，开关频率为10 kHz。

为了验证光伏发电系统在模式I和模式II情况下对电网故障的穿越特性，首先构造如图4所示的电网跌落工况。其中，在t＜0.1 s时，电网三相电压对称，在t=0.1 s时，电网B、C相同时发生0.3 pu的电压跌落，持续时间为0.25 s，随后电网电压恢复到额定值。图4给出了上述跌落工况的三相电压波形及其标幺值波形，下面根据光伏阵列出力大小分别给出模式I和模式II情况下光伏发电系统有功功率和无功功率出力波形。

4.2 模式I仿真

如图5所示，当光伏阵列输出功率为6 kW时，光伏阵列输出的有功功率小于逆变器允许的最大功率限制值Pmax。据前文理论分析得知，电网电压跌落0.3 pu时逆变器有功出力的限制值约为16 kW，因此可将光伏阵列的有功功率率全部注入电网。将三相逆变器电流控制在最大允许值Imax以内，Boost升压斩波电路工作在最大功率点跟踪模式（MPPT）。图5中瞬时无功功率波动由电网电压不对称引起，其平均值约为30 kVar，此部分无功功率可用于对电网的动态无功支撑，改善系统稳定性。当t＞0.35 s时，电网电压恢复到额定值，此时无功功率参考值和实际值降低到零。

图4 PCC点电网电压及其标幺值波形图Fig.4 Waveform diagram of PCC grid voltage and its PU

图5 模式I工况下光伏发电系统出力特性Fig.5 Output characteristic of PV generation system under the working conditions ofmode I

4.3 模式II仿真

如图6所示，当光伏阵列输出功率为26 kW时，光伏阵列输出的有功功率大于逆变器允许的最大功率限制值Pmax。据前文理论分析得知，电网电压跌落0.3 pu时逆变器有功出力的限制值约为16 kW，此时Boost升压斩波电路暂停最大功率点跟踪，并开始跟踪功率P*，Boost升压斩波电路与三相逆变器之间的功率不均衡问题通过控制三相逆变器直流母线电压来解决。在图6所示的电网发生0.3 pu两相跌落时，逆变器的有功出力被限制到最大允许值的16 kW，此时注入系统的瞬时无功功率在零上下波动，其平均值为零。实现了光伏发电系统的低电压穿越功能，同时保证了系统的安全稳定运行。当t＞0.35 s时，电网电压恢复到额定值，此时有功功率参考值和实际值恢复到光伏阵列的实际功率。

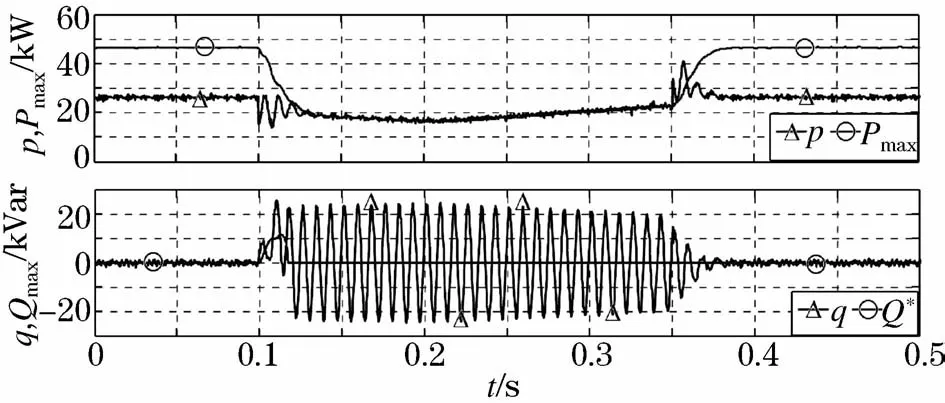
图6 模式II工况下光伏发电系统出力特性Fig.6 Output characteristic of PV generation system under the working conditions ofmode II

5 结束语

针对传统光伏发电系统在电网故障条件下穿越控制策略的不足，提出一种基于模糊神经网络的光伏发电系统功率控制方法。在电网电压突变和跌落情况下能够快速地调整光伏发电系统的工作模式，以适应光伏阵列最大输出功率和并网逆变器额定容量及最大输出电流的限制，具有稳定性强、跟踪速度快等优点。给出了控制策略总体架构，详细阐述了电网故障控制器运行模式切换策略，建立了模糊神经网络算法的数学模型和实现流程，并在Matlab/Simulink平台下搭建了仿真模型，最后在该模型上验证了所提出控制策略的有效性。