基于改进型软件锁相环的正负序分量分离新方法研究*
郭凯,程启明,程尹曼,黄伟,徐聪
(1.上海电力学院自动化工程学院,上海200090;2.上海电力公司市北供电分公司,上海200041)
0 引 言
随着新能源及柔性交流输电的应用和发展,电力电子变流器的应用也变得非常普及。三相变流器的控制需要检测电网的基波分量,在电网无故障稳态运行情况下,三相变流器可以很容易的控制,但在电网发生不对称故障或不平衡运行情况,能否快速而准确的提取电网的正负序的基波分量对三相变流器的正常运行和控制就变得尤为重要[1-4]。
在电网不平衡条件下的电力电子变流器的控制策略中,需要对电网电压和并网电流进行正负序分量检测,实现对正负序分量的独立控制[5-7]。目前,传统的正负序分量分离方法主要有低通滤波器法、T/4延时法[8]、dq变换法、延时信号消除(Delay Signal Cancellation,DSC)级联法、二阶广义积分器(Second Order Generalized Integrator,SOGI)法 等[9-10]。其中:低通滤波器法当截止频率较低时响应速度慢,而截止频率高时谐波又不能完全滤除,且滤波器会对控制系统参数造成一定的藕合影响;T/4延时法在电网电压有畸变或频率不稳定时,不能准确分离出正负序分量;dq变换法需在两个或更多的同步旋转坐标系下对被测量解藕,计算量较大,而且在电网有谐波的情况下,并不能准确分离;DSC级联法只能消除特定次数的谐波,当要完全消除谐波时,由于级联数太多而造成计算量太大;SOGI法对电网中低次谐波的滤除效果不是很理想。
提出一种基于改进型软件锁相环的正负序分量分离方法。这种方法中,采用SOGI消除高次谐波,采用正负序级联的DSC消除低次谐波,并结合软件锁相环(Software Phase-Locked Loop,SPLL)的锁相功能来提取电网中的正负序分量的方法。MATLAB/Simulink仿真结果验证了本文所提出的改进型SPLL法远优于常用的传统SPLL、T/4法、DSC法、SOGI法和SIGIDSC法。
1 常规的软件锁相环原理
常规软件锁相环(SPLL)的基本结构如图1所示[8]。当电网三相对称时,在电网电压定向情况下,通过αβ变换和dq变换,uq和给定信号经过PI调节得出为频率偏差,然后与给定频率相加后得到的就是电网电量的角频率,再经过积分环节,为电网的相位,最后将电网的频率和相位锁定。而当电网电网不平衡时,经过dq变换的q轴上的电压除了直流分量,还含有交流分量,因此传统SPLL在电网电压不平衡时,失去锁定电网电压基波的能力。
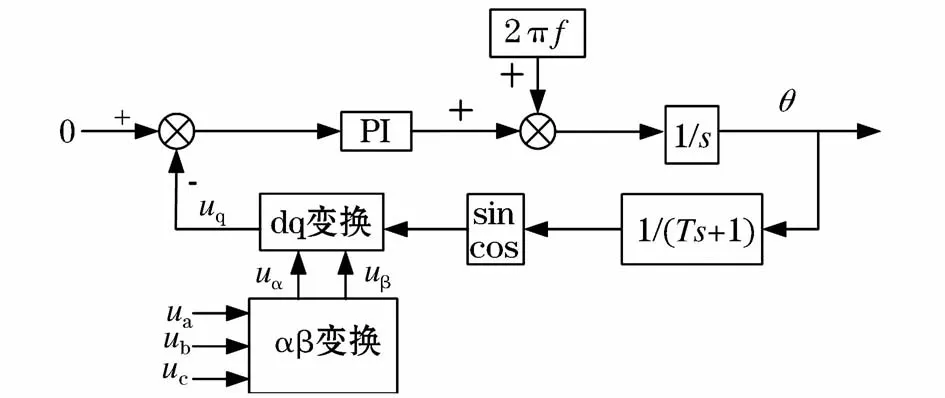
图1 常规软件锁相环(SPLL)的基本结构Fig.1 Basic structure of a conventional SPLL
图中,θ是电网电压旋转相量的相位角,αβ变换和dq变换分别为(忽略零序分量):
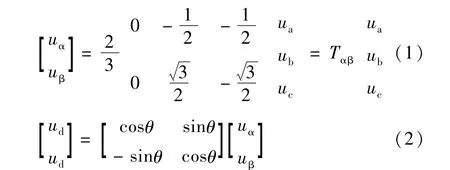
2 基于改进型软件锁相环的正负序分量分离方法
2.1 正负序分量分离的总体结构
在三相三线制情况下,零序分量为零,忽略不计,当电网出现不平衡运行情况时,实现电网电压正负序基波分量的分离。本文在αβ变换环节加入SOGI环节,在dq变换中加入正负序级联DSC环节,从而使改进后的SPLL可以准确锁定电网的频率和相位,进而得到电网的正负序分量。图2为提出的基于改进型SPLL的正负序分量分离原理框图。
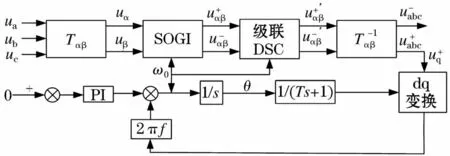
图2 基于改进型SPLL的正负序分量分离原理框图Fig.2 Block diagram of the separation of positive and negative sequence component based on improved SPLL
2.2 SOGI环节
图3为二阶广义积分器(SOGI)在改进型SPLL中的功能图。图中,上标“+、-”代表正负序分量,“α、β”代表经过坐标变换后α轴和β轴上的分量。
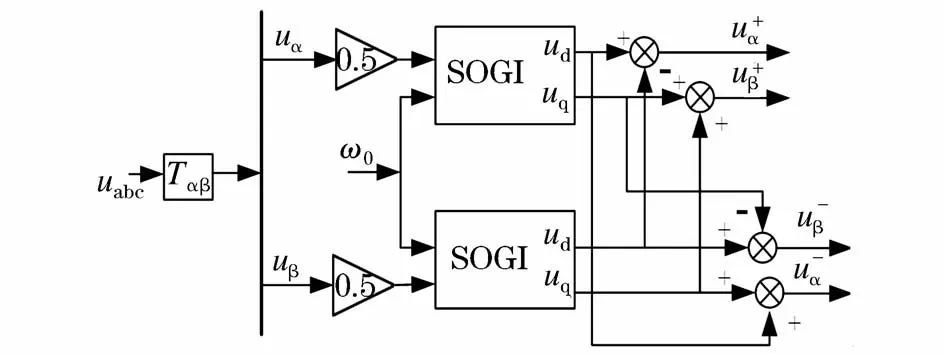
图3 SOGI在改进型SPLL中的功能框图Fig.3 Functional block diagram of SOGI in improved SPLL
由图3可得:

式中 q=ej90°,是通过SOGI实现90°的移相功能。
二阶广义积分器(SOGI)的电路结构如图4所示。图中k为阻尼比,ω0为无阻尼自然频率。
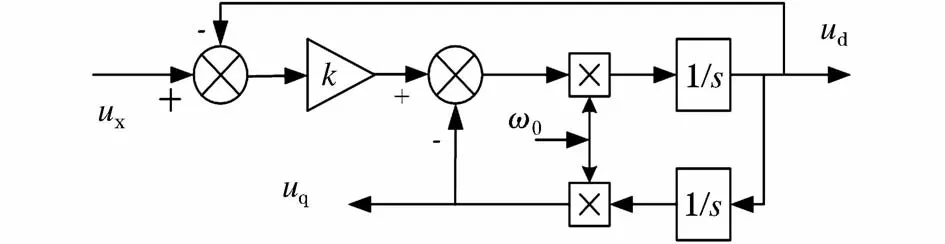
图4 二阶广义积分器(SOGI)的结构Fig.4 Structure of SOGI
由图4可得传递函数为:
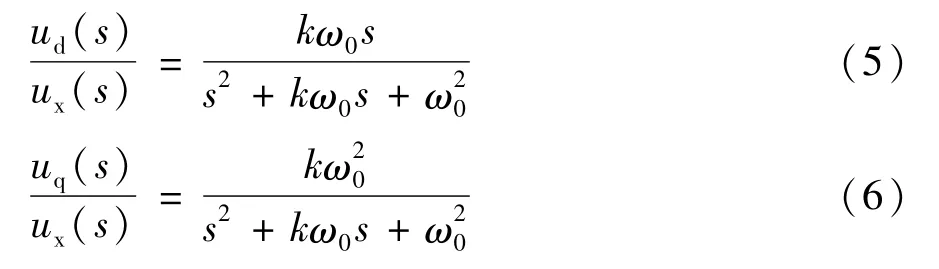
图5为SOGI的波特图,图5(a)对应式(5),图5(b)对应式(6)。由图可见,k值的大小影响着系统的带宽。综合系统的响应速度和滤波效果,k值可选为1.4。由相频特性图可见,在ω0(此时取50 Hz)为电网基波频率(即SPLL频率输出)时,输出ud与输入同相位,输出ud相差90°,且两者与输入频率相同。由幅频图可见,在基频以上,随着频率增加,输出幅值减小。因此,SOGI对低次谐波,输出幅值衰减较少,滤波效果并不理想;SOGI对高次谐波,幅值衰减较大,滤波效果较为理想。由于SOGI的频率输入为SPLL的锁定的电网电压的频率,因此当电网电压频率变化时,SOGI的滤波效果并不受无阻尼自然频率ω0变化的影响。
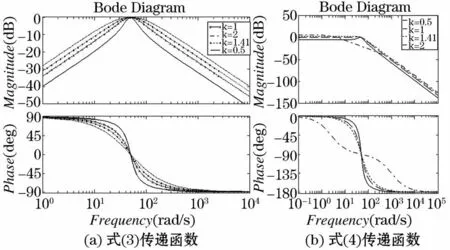
图5 SOGI的波特图Fig.5 Bode diagram of SOGI
2.3 正负序级联的DSC环节
由SOGI的波特图可见,SOGI具有滤除谐波的作用,尤其是对高次谐波作用特别有效,但是对低次谐波的滤除效果不是很好。由于电网中的谐波成分中5、7次谐波的含量最多,SOGI对5、7次谐波即低次谐波滤除效果不是很明显。因此,为了弥补SOGI这方面的不足,本文加入了正负级联的DSC环节进行改进,以滤除经过SOGI的没有完全消除的5、7次谐波。
在正序旋转坐标系中,正序分量为直流量、负序分量为二倍频的负序基波分量、n次谐波则变为n-1次谐波。在负序旋转坐标系中,负序分量则为直流量、正序分量为二倍频的正序基波分量、n次谐波则为n+1次谐波。因为旋转坐标系中的谐波仍然是正弦波,因此可以利用DSC进行消除谐波[15]。在dq+、dq-坐标系中,分别可得:
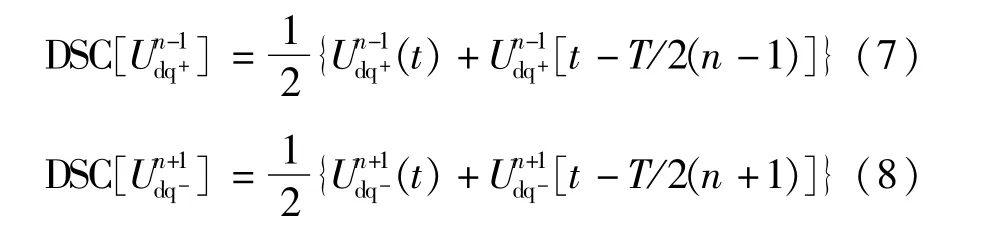
式中 T为基波分量周期;n为第n次谐波;下标d、q分别表示d轴、q轴坐标上的分量。
理论上利用正负序级联算法可以消除任意次谐波,本文利用级联的DSC算法消除系统中大量存在的5、7次谐波。考虑到延时对PLL系统的动态响应和稳定性的影响,将dq坐标系中的DSC级联算法转换到αβ坐标系中。在αβ坐标系中DSC算法为:
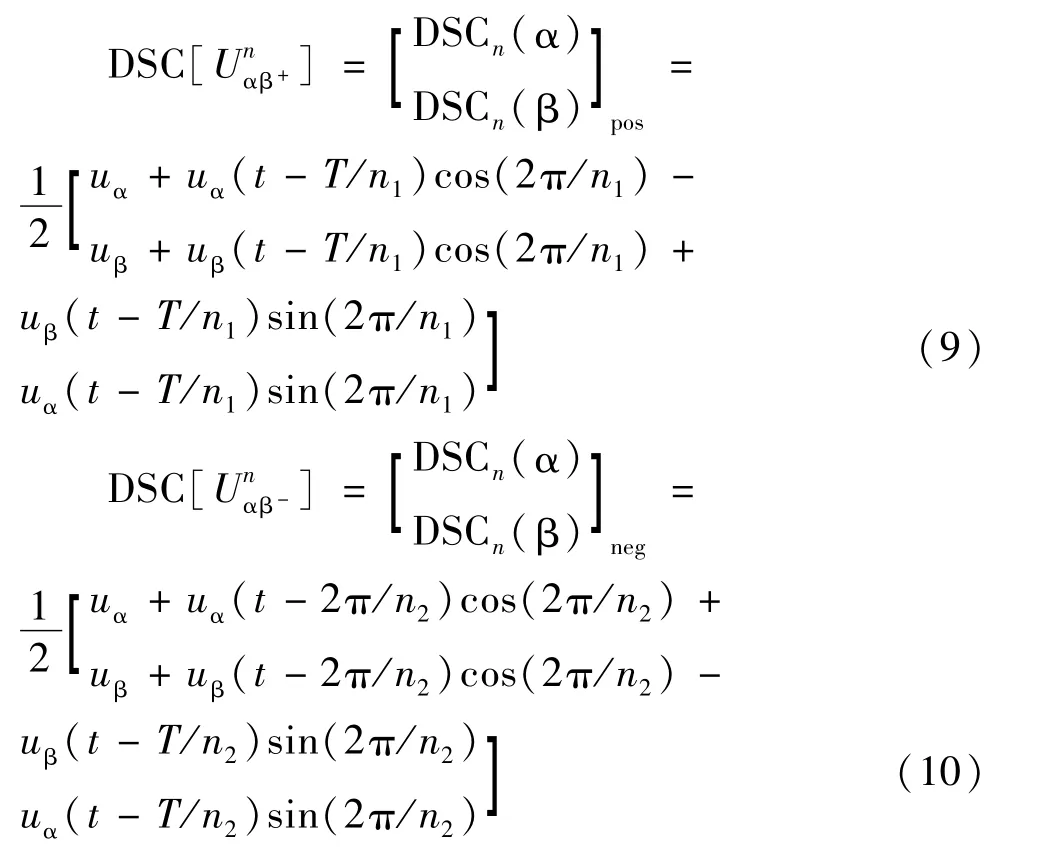
式中α、β为分别表示坐标轴α|β上的电压分量即uα、uβ;下标 pos、neg分别表示正、负序分量;分别取值为 n1=2(n-1)、n2=2(n+1)。本文为消除 SOGI滤波效果不理想的5、7次谐波,其中:为消除正序中的负序分量和5、7次谐波n1取4和8;为了消除负序中的正序分量和5、7次谐波,n2取4和16。图6为本文正负序级联DSC的原理框图,采用两级级联的DSC,其中第1级级联时消除5次谐波,第2级级联消除7次谐波,T是根据SPLL的得到实时的电网电压的基波周期。
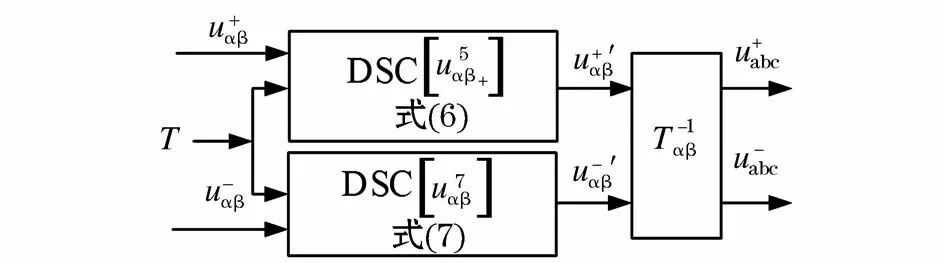
图6 正负序级联DSC的原理框图Fig.6 Block diagram of cascade DSC of positive and negative sequences
经过级联后的电压αβ轴上的正负序分量就完全分开来,其中正负序分量经过变换就得到了三相的正负序分量,αβ轴上的正序风量经过2s/2r变换后的q轴分量反馈给SPLL结构,由此来锁定电网电压的基波频率,从而由SPLL准确给SOGI和DSC提供实时的电网的基波频率保证SOGI和DSC进行正确的正负序分量的分离和谐波的消除。
其中两相静止坐标系到三相静止坐标系的变换公式为:
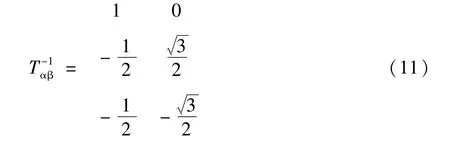
3 仿真实验与讨论
在MATLAB/Simulink仿真软件上对本文提出的新的正负序分离方法与传统SPLL法、T/4法SOGI法、DSC法和SOGIDSC法这5种常用方法进行仿真对比,以说明本文方法的优点。
下面在电网电压平衡、不平衡和频率变化等3种情况下进行仿真与讨论。仿真中,k取为1.4,SPLL中的f取为50 Hz,仿真时间取为0.1 s。由于基波正序和基波负序都是对称的,因此仅取a相电压曲线进行分析。
(1)情况1:电网电压情况时
这种情况下,电网工作于平衡情况且无谐波,频率为恒定50 Hz,其电压波形如图7所示。
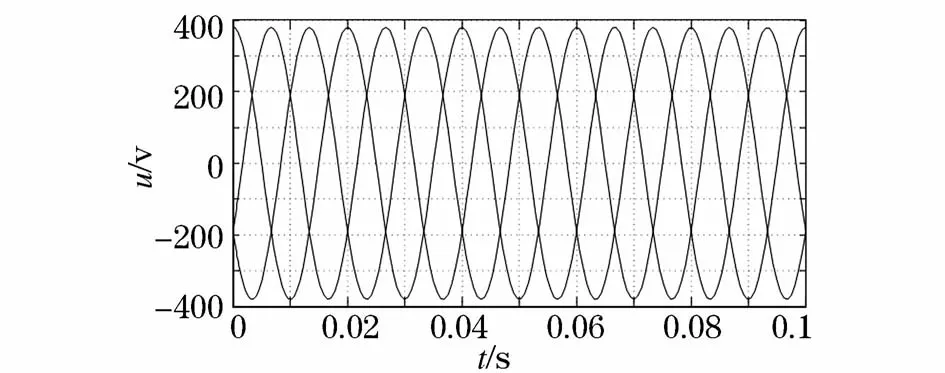
图7 电网平衡时电压波形Fig.7 Voltage waveform in balanced grid
此情况下仿真波形如图8所示。其中:图8(a)~图8(f)分别改进型 SPLL、传统 SPLL法、SOGIDSC法、T/4延时法、DSC法和SOGI法的基波电压波形,各子图上的实线、虚线分别为电网、锁定的基波电压波形。图8(a)、图 8(c)、图 8(d)、图 8(e)和图 8(f)的上、下子图分别对应正序、负序电压。
由图可见,在电网对称状况下,本文所提出的改进型SPLL和其它5种方法都可以锁定电网基波。从锁定时间长短来看,传统SPLL法、T/4延时法、改进型SPLL法、DSC法、SOGI法和SOGIDSC法依次由短到长。本文提出的改进型SPLL法从锁定效果和时间上来说,在6种方法中处于中上等。
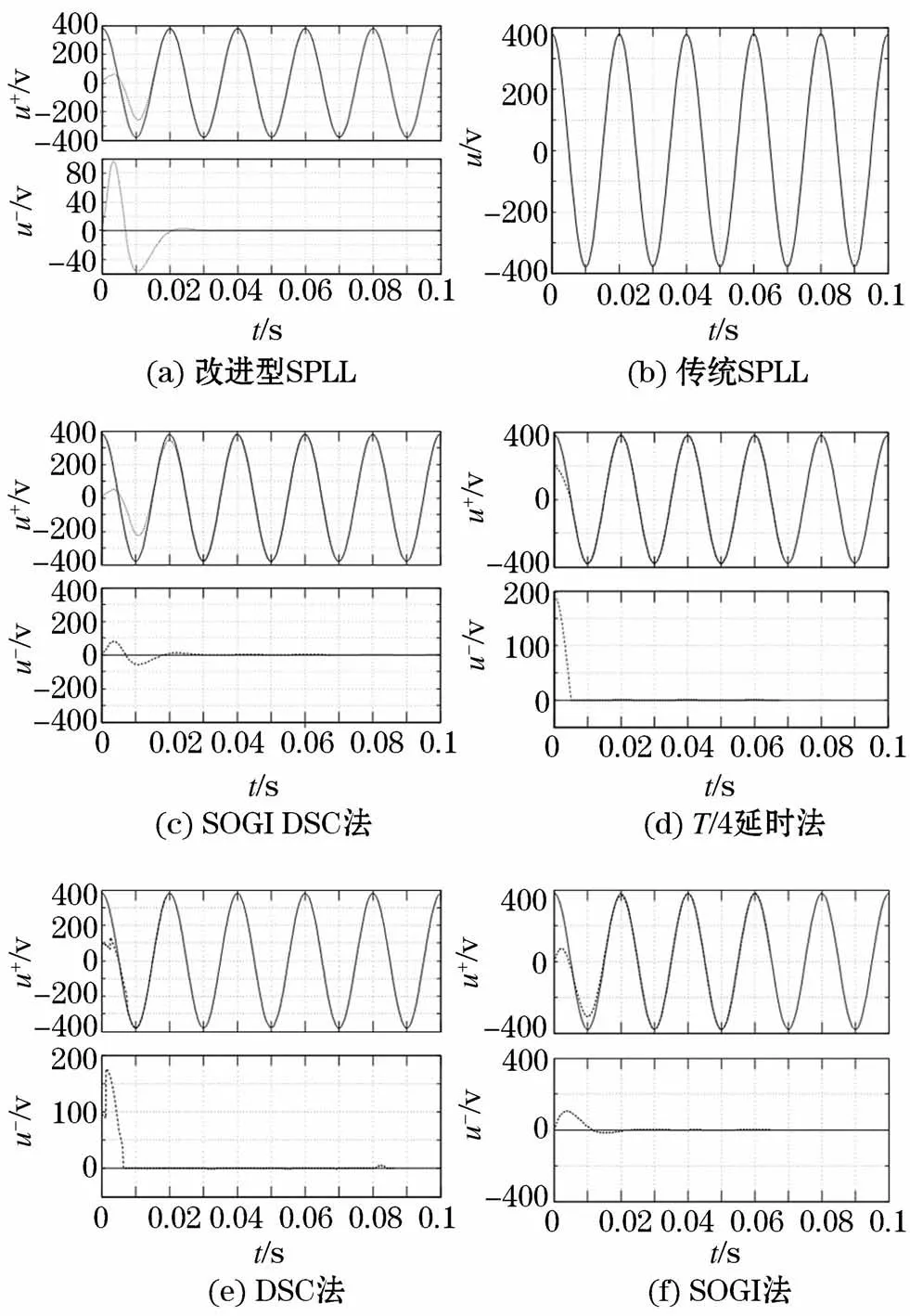
图8 电网电压对称时的仿真波形Fig.8 Simulation waveform when the grid voltage is symmetrical
(2)情况2:电网电压不平衡时
此种情况下,电网加入幅值为380 V的正序电压和幅值为380 V的负序电压,并加了5次、7次、9次、10次和20次数谐波,它可模拟电网电压不平衡及电压畸变时的状况,其电压波形如图9所示。
在不平衡情况下仿真波形如图10所示。其中:图10(a)~图10(f)分别改进型SPLL、传统SPLL法、SOGIDSC法、T/4延时法、DSC法和SOGI法的基波电压波形,各子图上的实线、虚线分别为电网、锁定的基波电压波形。图,10(a)、图 10(c)、图 10(d)、图10(e)和图 10(f)的上、下子图分别对应正序、负序电压。由图可见,只有本文所提出的改进型SPLL和SOGIDSC 2种方法可以很好的锁定电网正负序的基波风量,而其它4种方法已无法正确锁定电网基波风量。
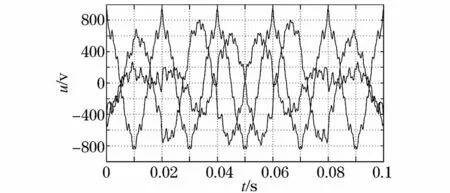
图9 电网电压不平衡时电压波形Fig.9 Voltage waveform in unbalanced grid voltage

图10 电网电压畸变时的仿真波形Fig.10 Simulation waveform when the grid voltage is unbalanced
(3)情况3:电网频率变化时
此种情况,设电网电压的基波频率为40 Hz,并加入负序分量和5次、7次、9次、10次和20次谐波。它可模拟电网频率发生变化的情况,其电网电压波形如图11所示。
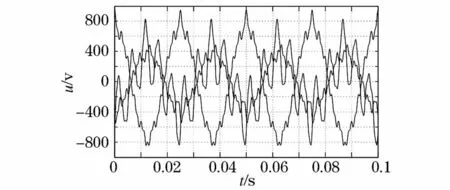
图11 频率变化时电压波形Fig.11 Voltage waveform when frequency changes
在频率情况下仿真波形如图12所示。其中:图12(a)~图 12(f)分别改进型 SPLL、传统 SPLL法、SOGIDSC法、T/4延时法、DSC法和SOGI法的基波电压波形,各子图上的实线、虚线分别为电网、锁定的基波电压波形。图12(a)、图12(c)、图12(d)、图12(e)和图 12(f)的上、下子图分别对应正序、负序电压。由图可见,在电网电压频率发生变化的情况下,本文提出的改进型的SPLL同样可以快速锁定电网的正、负序基波分量,但其它5种方法不能锁定电网的正、负序基波分量。

图12 电网电压频率变化时的仿真波形Fig.12 Simulation waveform when the frequency of grid voltage changes
总之,在电网平衡时,本文的改进型SPLL与其它5种方法都能锁定正、负序基波电压波形,只是改进型SPLL时间慢于SPLL法和和DSC法;在电网不平衡时,只有本文提出的改进型SPLL和SOGIDSC法锁定电网基波分量,而其它4种方法不能锁定电网基波分量。在频率变化时只有本文提出的改进型SPLL能锁定电网基波分量,而其它5种方法不能锁定电网基波分量。因此,提出的改进型SPLL的总体性能远优于其5种方法。
4 结束语
利用SOGI较好的高次谐波滤波以及移相功能,并加入正负序级联的DSC来弥补SOGI对低次谐波滤波效果不理想的缺点,来改进传统的SPLL,进而实现电网正负序分量的分离。本文提出的改进型SPLL在电网平衡、不平衡以及频率变化的情况下,都可以很好的锁定电网的基波分量,分离出电网的正、负序基波分量,MATLAB/Simulink仿真结果验证了本文提出的改进型SPLL方法远优于常用的传统SPLL法、T/4延时法、DSC法、SOGI法和SOGIDSC法等5种方法,它能快速、准确地分离出电网的正、负序基波分量。

