单相无桥Cuk功率因数校正器分析与设计*
刘陈琼,周群
(四川大学电气信息学院,成都610064)
0 引 言
随着电力电子装置的广泛应用,电网中的谐波污染日趋严重,最有效的解决办法就是对用电设备进行功率因数校正。为了满足相应的国际标准(如IEC 61000-3-2)[1],有源功率因数校正器(active power-factor correction,APFC)在电力电子领域中被广泛应用[2-7]。
与其他变换器相比,Cuk变换器是通过电容传递能量,具有输入输出电流连续,输入输出电流纹波小以及很宽范围的输出电压等优点,因此,Cuk变换器应用于APFC变换器中是一种很好的拓扑结构。传统Cuk PFC变换器[8]存在前端二极管整流桥,增加了变换器电流导通路径的损耗,降低了变换器效率。为了提高PFC变换器的效率,文献[9-10]提出了无桥Cuk变换器,消除了传统Cuk PFC变换器中的二极管整流桥,减少了电流导通路径中功率器件数量,大大提高了变换器的效率。然而文献[9]中 Cuk PFC变换器工作于DICM模式(discontinuous inductor currentmode,DICM)具有开关管电流应力大,导通损耗高,输入电流纹波大等缺点,本文根据电感和电容的对偶性,分析了工作于不连续电容电压模式(discontinuous capacitor voltagemode,DCVM)的 Cuk PFC变换器的工作原理,对其工作特性进行了详细的分析,其次给出了无桥Cuk PFC变换器的电路参数设计,最后通过仿真分析验证了工作于DCVM模式的无桥Cuk PFC变换器的低开关电流应力,低输入电流纹波以及开关管的零电压关断和输出二极管零电压导通的性能。
1 无桥Cuk PFC变换器工作原理
1.1 稳态分析
图1为无桥Cuk PFC变换器[9],它由两个分别工作于输入电压正半周和输入电压负半周的Cuk变换器构成。开关管Q1和Q2采用同一个驱动信号,且不需要隔离驱动,控制电路简单,需要注意的是Cuk变换器是负极性输出电压。输入电压正半周时,Cuk PFC变换器由输入电感L1,电容C1,开关管Q1,输出电感Lo1,输出二极管Do1以及整流二极管Dp构成。输入Lo1电压负半周时,Cuk PFC变换器由输入电感 L2,电容 C2,开关管 Q2,输出电感 Lo2,输出二极管Do2以及整流二极管Dn构成。由于变换器的对称性,本文只重点分析输入电压正半周时Cuk PFC变换器的稳态特性,负半周与正半周类似,不再赘述。

图1 无桥Cuk PFC变换器的电路结构Fig.1 Circuit structure of bridgeless Cuk PFC converter
为了简化分析,变换器工作在稳定条件下假设:
(1)输入电压是单一频率的正弦信号,开关频率fS远远高于输入电压频率fL;
(2)电感L1和L2足够大以致于通过它们的电流在一个开关周期TS内被当作常数;
(3)输出滤波电容Co足够大,在输入电压的工频半周期TL/2内Vo为常数;
(4)电容C1和C2足够小使Cuk变换器工作于DCVM模式。
在一个开关周期Ts内,工作于DCVM模式的Cuk变换器有三种不同的工作状态,由工作状态分析可得输入电压Vac为正半周时在一个开关周期TS内的理论稳态波形,如图2所示。
状态Ⅰ:开关管Q1导通,由于电容C1上的电压极性下正上负,二极管Do1反向截止。电源Vac充电给电感L1和Lo1,电容C1放电给负载。当电容C1两端电压线性减小到零时,工作状态Ⅰ结束。

图2 一个开关周期T S内Cuk PFC变换器工作于DCVM模式的理论波形Fig.2 Theoretical DCVM waveforms during one switching period T S for Cuk PFC converter
状态Ⅱ:开关管Q1仍导通,二极管Do1开始导通,电源Vac继续充电给电感L1,电感Lo1放电给负载,这一过程持续到开关管Q1关断。
状态Ⅲ:开关管Q1关断,二极管Do1仍处于导通状态,电流iL1充电给电容C1,电容两端电压由零线性增加,在一个开关周期结束时,电容C1的电压达到最大值VCM。
由图2的DCVM Cuk变换器的理论工作波形可以得到在一个开关周期Ts内电容C1的电压vC1为:

其中IL1和ILo1为电感L1和Lo1的平均电流,D1为电容C1的归一化放电时间,D为开关管 Q1的占空比。
由式(1)可得电容C1两端的最大电压VCM为:

稳态工作时,在一个开关周期TS内,电容C1的平均电流IC1为零,可得D1和D的关系式为:

稳态工作时,在一个开关周期TS内,电感L1和电感Lo1两端的平均电压为零,可得:

由式(2)和式(4)可得DCVM Cuk PFC电路的等效输入电阻Re为:

由式(6)可知,对于给定的占空比D和开关频率fS,等效输入电阻Re是恒定的。
假设输入电压Vac为理想的正弦信号,即:

式中Vm是输入电压的最大幅值;ω是输入电压的角频率。
由式(6)和式(7)可得半个工频周期TL/2输入电感电流iL1为:

由式(8)可知,当占空比D和开关频率fS固定时,输入电感电流随输入电压呈正弦变化,因此,DCVM Cuk电路具有自动PFC功能。
1.2 DCVM实现条件
定义d1(t)是归一化放电时间D1的变化量,根据式(4)、式(5)和式(7)可得 d1(t)与时间 t的关系式为:

由式(9)可知,当输出直流电压Vo和占空比D一定时,归一化放电时间d1(t)变量随输入电压Vac的变化而变化。
根据输入和输出能量平衡[11]Eout=ηEin可得占空比D为:

其中增益M为输出电压Vo和Vm之比,η为转换效率,定义无量纲参数K为:

由式(11)可知,当输出电压,转换效率以及参数K确定后即可算出占空比D。
Cuk变换器工作于DCVM模式,满足的条件是d1(t)<D,将式(9)和式(10)整理后可得临界连续电容电压模式(CCVM)的参数Kc和断续电容电压模式(DCVM)的参数K的关系式为:


DCVM Cuk变换器由于输入电感的电感值很大,当开关管在关断瞬间开关管两端会产生很高的电压应力,由图2可知开关管的电压应力等于中间储能电容C1两端的最大电压VCM,即:

由式(13)可知,参数K值越小,所对应的开关管电压应力越高,因此,参数K和开关管的参数选择根据实际电路进行合理选择。
图3是不同电压增益M条件下,参数Kc与ωt的关系图。式(12)表明当增益M确定时,参数Kc随时间t在一定范围内变化;当参数K<Kc时,Cuk变换器工作于DCVM,K值越趋近于Kc,变换器越容易进入CCVM。因此,在进行实际电路参数设计时,当确定变换器的增益后就可以对参数K在相应范围内进行合理取值。

图3 参数K c与ωt的关系曲线Fig.3 Relation curve of K c and duty cycleωt
2 电路参数设计和仿真分析
2.1 电路参数设计
为了验证工作于DCVM模式的无桥Cuk PFC变换器的可行性,设计变换器工作条件为110 V/50 Hz交流输入电压,输出电压Vo=-48 V,开关频率fS=50 kHz,输出功率115W(RL=20Ω),转换效率η=90%。
由式(11)可以得到C1(C2)需要满足的条件是:

由输出电压和输入电压可得增益M=0.3,根据图3可取参数K=0.04,此时开关管两端电压应力约为490 V,选取开关管型号为 IPW60R045CP:650 V,60 A,RDS-ON=45 mΩ。由式(10)可以计算出占空比D为39%。由式(14)可以计算出电容C1为40 nF,设计时可取39 nF/630 V的金属化薄膜电容。
DCVM Cuk PFC变换器中当开关管Q1截止时,电感L1和电容C1容易发生串联谐振,当发生串联谐振时电感L1和电容C1两端相阻抗最小,接近短路,这种情况对于输入电压源Vac是不允许发生的,因此,电感L1和电容C1发生谐振周期要远远大于开关管截止时间,则满足条件的关系式为:
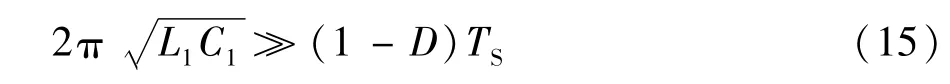
电感参数设计中还需要考虑电感本身存在电抗,为了减小对功率因数的影响,电感L1本身的电抗要远远小于输入等效电阻Re,则满足条件的关系式为:

将式(6)代入式(16)中,整理式(15)和式(16)可得输入电感L1需要满足的条件为:

将参数C1、占空比D以及输入电压频率和开关频率代入式(17)中,最后输入电感参数设计为L1=L2=9.3 mH。
同理,在开关管Q1导通时间内,电容C1和等效电感Le(Le=L1//Lo1)容易产生并联谐振,这样电容和电感两端电压会升高,当电压升高到超过电容C1的耐压值后会发生爆炸。为了避免谐振的产生[9],其谐振频率必须远远小于开关频率fS,等效电感Le满足的条件是:

将已知的参数值代入式(18)中,最后输出电感参数设计为Lo1=Lo2=300μH。
输出滤波电容Co足够大来保证输入功率随时间变化中能够为负载提供恒定的输出功率。定义低频输出电压峰-峰值纹波 Δvo[9]为:

其中Io为输出电流的平均值,由输出电压纹波<5%从而得到最后输出滤波电容Co参数设计为6 600μF。
2.2 仿真分析
采用PSIM仿真软件对无桥DCVM Cuk PFC变换器进行仿真分析,结果如图4~图7所示。图4为交流输入电压、输入电流和输出电压的仿真波形,图5为电容C1和C2两端电压波形,图6为驱动脉冲,输出二极管电流和电压,开关管电流和电压以及电容电压vC1的波形,图7为输入电流iac的谐波分析图,由图7可知,输入电流的各次谐波都远远小于IEC 61000-3-2 class C规定的谐波最大值限定标准,且THD为1.02%。
由图4~图7可知,无桥DCVM Cuk PFC变换器输入电流与输入电压同相,实现了单位功率因数,而且输入电流纹波小。电容C1和C2分别工作于正负半周,工作原理一致,电容两端最大值电压等于开关管电压应力,约为490 V,与理论计算一致,验证了理论设计的正确性。开关管和二极管具有低电流应力,并实现了开关管的零电压关断和输出二极管零电压导通,电容C1工作于电压不连续模式。

图4 输入电压V ac、输入电流i ac和输出电压V o的波形Fig.4 Waveform of input voltage V ac,input current iac and output voltage V o

图5 电容电压v c1、v c2的波形Fig.5 Waveform of capacitor voltage v c1 and v c2
由图4~图7可知,无桥DCVM Cuk PFC变换器输入电流与输入电压同相,实现了单位功率因数,而且输入电流纹波小。电容C1和C2分别工作于正负半周,工作原理一致,而且电容两端最大值电压为开关管电压应力约为490 V,与理论计算一致,验证了理论设计的正确性。开关管和二极管具有低电流应力,而且实现了开关管的零电压关断和输出二极管零电压导通,电容C1工作于电压不连续模式。

图6 变换器的主要工作波形Fig.6 Main operating waveform of converter

图7 输入电流i ac的谐波分析图Fig.7 Harmonic analysis diagram of input current i ac
3 结束语
本文研究了工作于不连续电容电压模式的无桥Cuk PFC变换器,详细分析了它的稳态过程和DCVM模式实现条件,并给出了DCVM模式下变换器的参数设计。分析结果表明,该变换器具有自动PFC功能,可实现单位功率因数。最后,通过仿真证实了理论分析的正确性和参数设计的可行性。同时,仿真结果显示了DCVM模式下的变换器输入电流总谐波畸变小,且可实现开关管的零电压关断和二极管零电压导通,提高了变换器的效率。

