不平衡电网电压下MMC的比例降阶谐振控制策略*
宋平岗,吴继珍,邹欢
(华东交通大学电气与电子工程学院,南昌330013)
0 引 言
基于电压源型换流器(voltage source converter,VSC)的高压直流输电(high voltage direct current,HVDC)技术凭借其可同时独立调节有功和无功功率,具有向无源网络供电以及不存在换相失败问题等技术优势,近些年在新能源并网、海上作业平台供电以及异步互联的不同供电城所中得到了广泛应用[1-2]。但传统的VSC-HVDC系统也存在电压等级过低和容量偏小等约束,模块化多电平换流器(modularmultilevel converter,MMC)的出现很好地解决了上述技术缺陷,使得HVDC技术得到了迅速发展;西门子公司所设计的“trans bay cable”和我国南汇风电场的示范工程均是MMC-HVDC实际工程[3-4]。
在MMC-HVDC实际运行中,电网电压可能出现不对称故障,此时将引起交流电流增大、直流电压出现二倍频波动、MMC子模块电容电压波动更为剧烈以及桥臂出现零序环流等问题,影响着HVDC工程电能的传输质量,严重时将是整个HVDC系统损坏崩溃[5]。传统的VSC-HVDC在电网电压不平衡时主要有抑制负序交流电流和抑制交流有功功率二倍频波动两个控制目标,而对于MMC由于储能电容分布于各子模块中,即使实现了这两控制目标,内部依然存在零序环流,零序环流进入直流侧将引起直流电压二倍频波动。文献[6-9]分别建立电网电压不平衡时MMC的相关数学模型,提出了在dq坐标系下的正、负序双电流环的控制策略,但双电流环增加了控制器的复杂程度和调试难度;文献[10]基于比例谐振调节器设计了交流系统不对称时的控制系统和零序环流抑制控制器。文献[5]利用反馈线性化理论设计相关非线性控制器,但仍是双电流环控制。
为了保证MMC-HVDC系统在电网电压不平衡时依然正常运行,文章提出一种基于比例-降阶谐振(proportional reduced-order resonant,P-ROR)调节器的MMC不平衡控制策略,在αβ坐标下分别针对两种控制目标设计相关控制系统将传统双电流环控制器个数降低为一个;同时利用该调节器器设计环流抑制控制器以抑制零序环流,最后在PSCAD/EMTDC中搭建仿真模型验证所提出的控制策略。
1 MMC数学模型
如图1所示为MMC单相等效基本电路,三相MMC由三个相单元组成,每个相单元分为上、下两个桥臂,其中桥臂由N个子模块和电感L串联而成,图1虚线框内为半桥型子模块拓扑图,R为桥臂等效损耗电阻。根据基尔霍夫定律和文献[6-10],可得MMC的相关数学方程:

式中 usj和 isj为 MMC第 j(j=a、b、c)相交流侧电压和电流,udc和idc为MMC直流侧电压和电流;ujp和ujn分别为j相上、下桥臂投入子模块电压总和,ijp和ijn为上、下桥臂电流;ej为MMC内部电动势;udiffj和idiffj为MMC内部不平衡电压和电流,其中idiffj由二倍频相间环流icirj和直流电流idc所组成。式(1)和式(2)分别为表示MMC桥臂电压和电流,式(3)表征着MMC交流侧和直流侧特性,式(4)表征着MMC相关内特性。
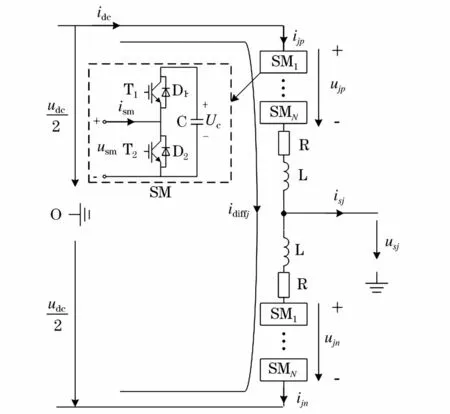
图1 MMC单相等效电路Fig.1 Single-phase equivalent circuit of MMC
2 电网电压不平衡相关分析
2.1 交流侧瞬时功率分析
当电网出现不平衡故障时,MMC交流输出电压和电流可以分解为正序、负序和零序分量;由于Y/Δ变压器隔断了零序分量的通路,故一般不考虑零序分量,因此将交流电压和电流表示为[10]:
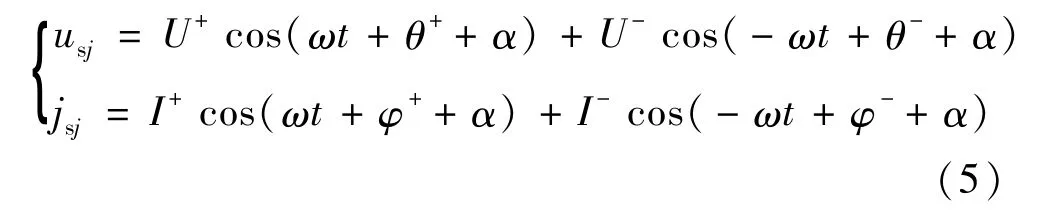
式中U+、U-、I+和I-分别正、负序电压的和电流幅值,θ+、θ-、φ+和φ-相应电压电流的初相角;ω为电网角频率;α为三相中电压与电压间、电流与电流间的相位差,A、B和C三相分别对应0°、-120°和120°。
将式(5)所表示的电压和电流方程在αβ坐标系下重新表示为:
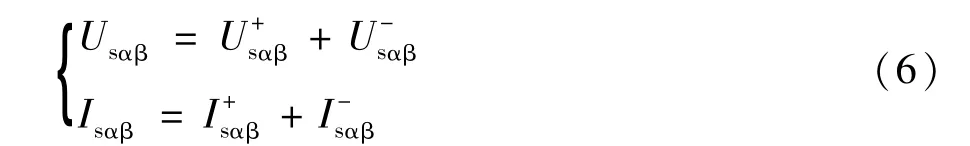
在αβ坐标系下MMC交流侧瞬时有功功率p和无功功率q可表示为:

将式(6)代入式(8)中,可得电网电压不平衡时的瞬时有功功率和无功功率:

式中p0和q0分别为有功功率和无功功率的直流分量;pc2和ps2为有功功率的二倍频波动分量;qc2和qs2为无功功率的二倍频波动分量。有功功率和无功功率各个分量由下式决定[11]:
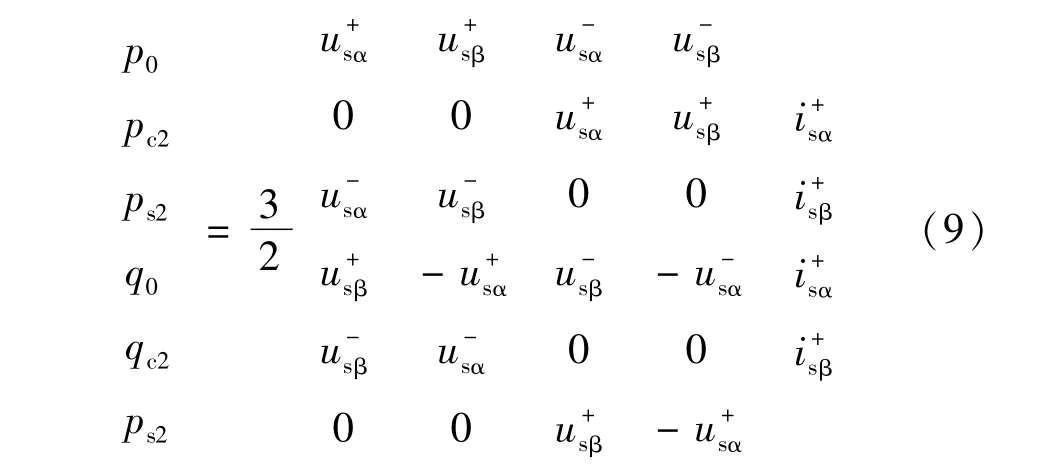
由式(9)和式(10)可知,当交流系统出现某一相电压跌落或故障接地时,由于电压和电流均存在负序分量,此时MMC输出有功功率和无功功率不再只是恒定值,均出现二倍频分量,此时为了保持额定功率的输送,交流系统将需要获取更大的电流,将引起MMC内部桥臂电流增大、子模块电容电压波动更为剧烈以及含有零序环流;MMC输出功率的二倍频波动,同时引起直流母线出现二倍频波动,因此必须采取合适的不平衡控制策略。
电网电压不平衡时,MMC有两个控制目标:
(1)控制目标1:抑制负序交流电流,保持MMC交流电流对称输出,此时 i-sα=i-sβ=0;
(2)控制目标2:抑制交流输出有功功率二倍频波动,消除直流电压的二倍频波动,此时pc2+ps2=0;
2.2 电网电压不平衡时MMC环流分析
在MMC运行过程中,由于电感的瞬时功率相对于整个相单元较小通常可以忽略不计,同时忽略MMC的内部损耗功率,且直流电压保持恒定,即udc=Udc;则无相关环流抑制策略运行时,MMC交、直流瞬时功率保持平衡[4]:

则不平衡电流idiffj可表示为:
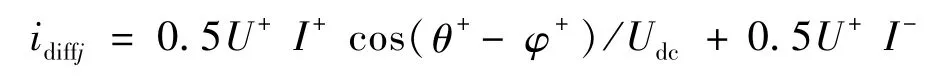
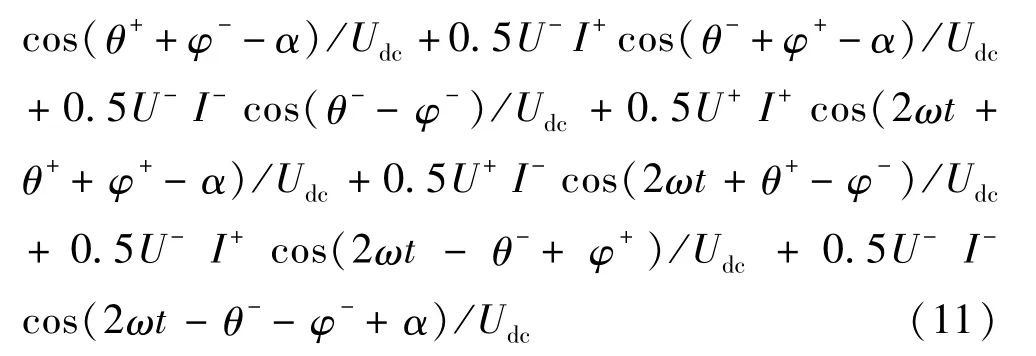
由式(12)可以发现,当电网电压不平衡时,MMC三相中的不平衡电流idiffj中直流分量不再相等,即直流电流在三相中不再均分;二倍频分量即环流icirj中包含正序、负序和零序分量,零序分量将进入直流侧引起直流侧二次波动。
当控制系统实现控制目标1时,由于负序电流被抑制,此时idiffj可以表示为:
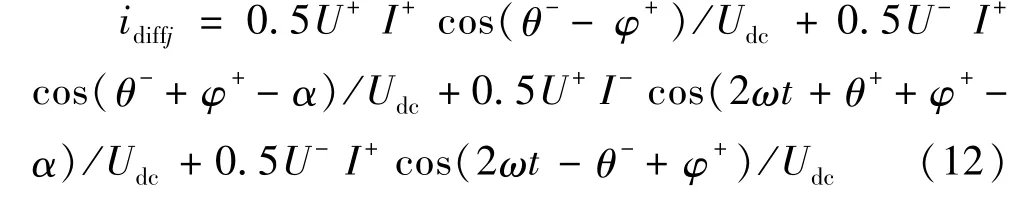
尽管不存在负序电流,但负序电压仍然存在,此时,直流电流在相单元不均分,环流中包含负序和零序分量。
当控制系统实现控制目标2时,交流输出有功功率二倍频波动被消除,此时idiffj可以表示为:
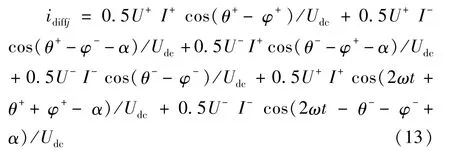
此时交流侧有功功率不存在零序分量,但直流电流在相单元仍然不均分;由文献[6]可知由于储能电容的分散布置,MMC三相中二倍频瞬时功率不对称时直流母线依然可能存在二倍频波动;即在控制目标2时,由于正序负序功率分量相叠加后,三相中必定有某一相二倍频功率幅值明显大于其他相时,此时直流母线就可能二倍频波动,该二倍频波动是由桥臂瞬时二倍频功率的正序和负序功率共同作用引起的,说明在控制目标2时环流中依然包含正序、负序和零序分量。
3 基于比例降阶谐振器的MMC不平衡控制系统
3.1 降阶谐振器
为了在αβ坐标系下设计电网电压不平衡下MMC的相关控制系统,文章引入降阶谐振(reduced order resonant,ROR)控制器对正弦信号进行调节,降阶谐振控制器的传递函数为[12-13]:式中ω为谐振频率,即为电网基波角频率。

实际中,为了增大ROR调节器在谐振频率处的带宽,通常引入一个截止频率ωc构成降阶准谐振reduced order quasi-resonant,ROQR)调节器,其传递函数表示为:

由于ROQR调节器存在复数j,不利于控制器的解藕设计,因此需要采用一定措施实现复数j。在αβ坐标系下,存在矢量 Xαβ=xα+j xβ满足:xα=j xβ、xβ=-j xα这一矢量关系为实现复数j提供了条件;假设矢量 Yαβ=yα+j yβ为矢量 Xαβ经 ROQR调节器的输出量,则:求得[14-15]:
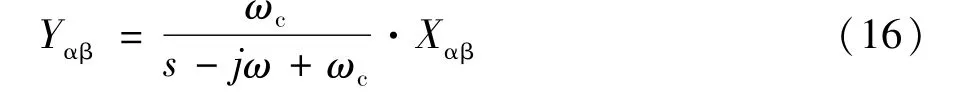
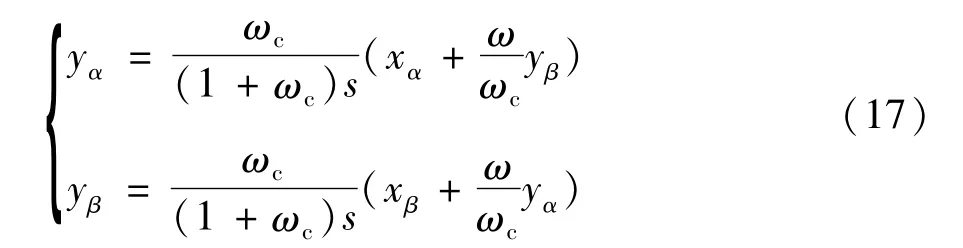
如图2所示为αβ坐标系下ROQR调节器的结构简图[12-13]。
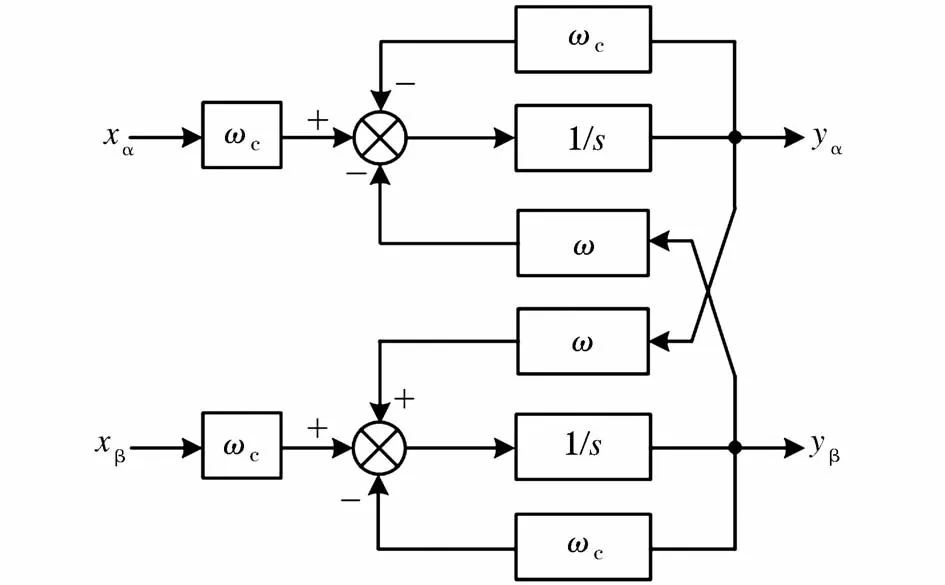
图2 降阶谐振调节器结构图Fig.2 Structure diagram of ROQR regulator
3.2 控制系统设计
为了保持MMC按照功率指令P*和Q*输出相应的功率,根据不同控制目标通过反解式(10)所表示的矩阵,可以得到相应的电流参考值[11,16]:
(1)控制目标1:
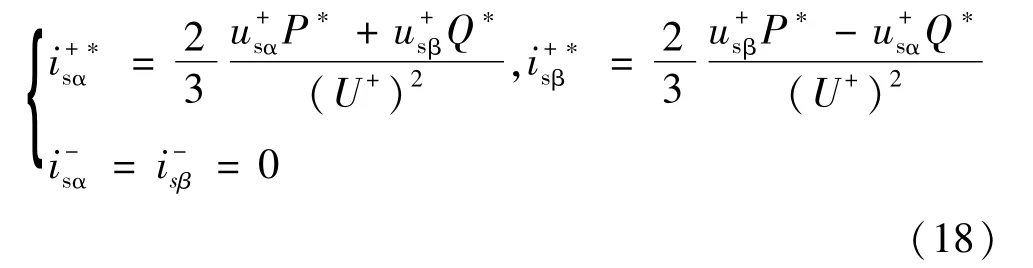
(2)控制目标2:

对于工作于定直流电压和定交流电压的MMC,可通过调节直流电压或交流电压获取相应的有功或无功功率指令。将式(3)所表示的MMC的交流特性方程在αβ坐标系下重新表述:
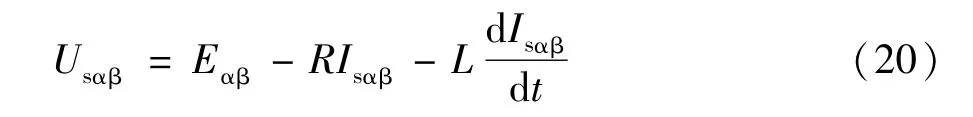
式中 Eαβ=[eα,eβ]T,Usαβ=[usα,usβ]T和 Isαβ=[isα,isβ]T为相应电气量在 αβ坐标系下的分量。
则根据式(19)~式(21)设计相关电流控制器即可获取电网电压不平衡时对MMC相应控制目标的内部电动势ej的参考值,从而实现相应的控制目标。
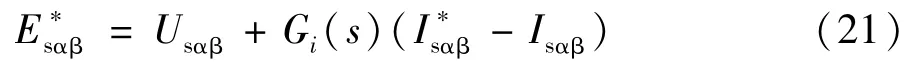
式中 上标带*的变量为相应电气量的参考值;Gi(s)为电流环控制器,利用比例和降阶谐振调节器构成,表示为:
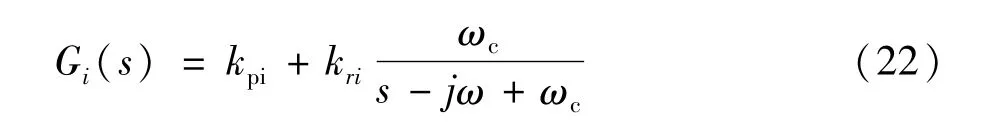
式中 kpi和kri分别为比例和谐振系数。
结合式(22)可以得到基于P-ROQR的不平衡电压时MMC电流控制系统框图,如图3所示。
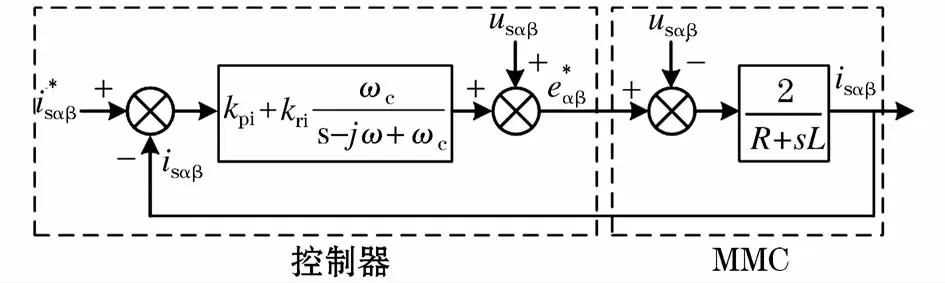
图3 电流环控制器框图Fig.3 Block diagram of current loop controller
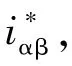
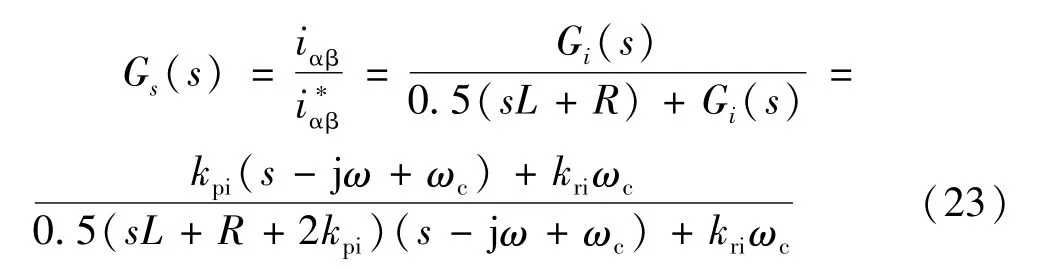
将 s=jω带入式(23)中,当 kpi>>R,kpi>>ωL,kri>>kpi时,|Gs(jω)|≈1;说明控制器在基波角频率ω处能够实现电流零稳态跟踪参考值。
3.3 环流抑制控制器设计
由第2.2小节分析可知,当电网电压不平衡时,MMC内部将可能流通着正序、负序和零序环流,因此需要设计相关环流抑制控制器。根据式(4)可以获取电网电压平衡时桥臂电流中的环流成分:

式中Idc为直流电流测量值idc低通滤波后的值。则由式(4)可知,环流的数学模型为[14]:

式中ucirj为相间环流icirj在桥臂电感和电阻中产生的电压;同理于电流环设计,可以得到MMC内部环流的控制方程:
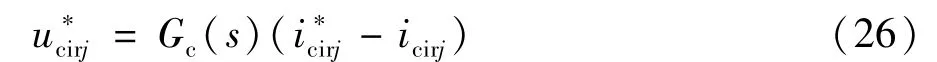
式中上标带*的变量为相应电气量的参考值;环流的参考值一般取0;Gc(s)为环流抑制控制器:
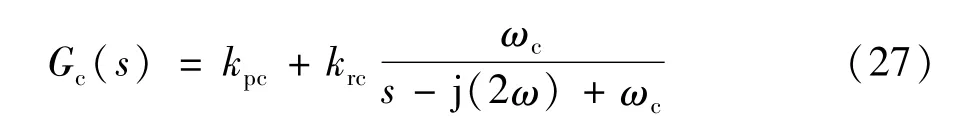
式中kpc和krc分别为环流抑制器的比例和谐振系数。
由于环流中包含正序、负序和零序分量,在αβ坐标系下需要将环流正序、负序和零序分量分离,且需要同时设计三个环流抑制控制器,增加控制系统的复杂性,为此文章在设计环流抑制控制器时不再将MMC三相环流转换至αβ坐标系下内设计系统,而是分桥臂设计,对单相桥臂而言并不存在正负序和零序问题,只要能够抑制100 Hz的正弦信号即可完全抑制环流的所有成分;但如何单相中实现ROR中复数j是系统设计的关键,文献[13]指出单相系统中可利用一阶全通滤波(all pass filter,APF)实现复数j,全通滤波器的传递函数为:

综上所述,可得环流抑制的控制原理图,如图4所示。
4 仿真分析
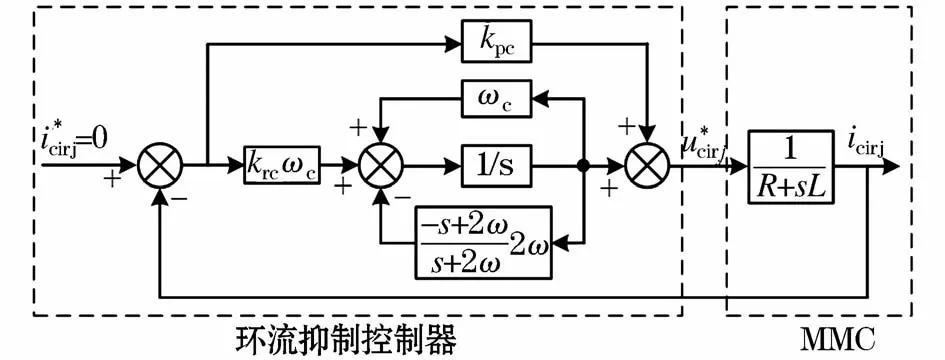
图4 环流抑制控制器Fig.4 Circulating current suppressing controller
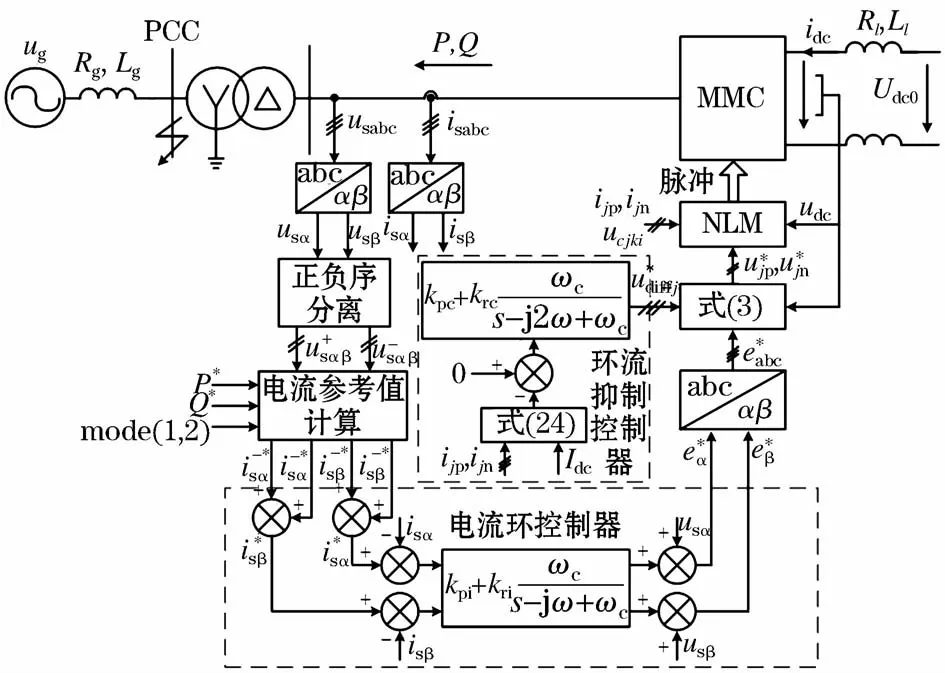
图5 仿真控制系统框图Fig.5 Block diagram of simulation control system
在PSCAD/EMTDC仿真环境中如图5所示的51电平MMC-HVDC仿真模型与控制系统,一端采用文章所提出的控制策略,一端稳定直流电压Udc为60 kV,直流线路使用集中参数等效,等效电阻Rl=0.5 Ω,等效电感Ll=0.32 mH。其他相关仿真系统参数如下:交流电网额定电压ug=110 kV,变压器变压比110 kV/35 kV,漏抗为0.1 pu;子模块电容值C=10 mF,桥臂串联电感L为10 mH,桥臂等效损耗电阻R=0.5Ω。
如图6所示为电网电压不平衡时两种控制目标的仿真结果,图6(a)为控制目标1的仿真结果,图6(b)为控制目标2的仿真结果。MMC向交流电网注入有功功率30 MW、无功功率为15 MVar;在0.5 s时PCC处A相出现故障接地,故障维持0.2 s后被清除,环流抑制控制器在0.6 s时启动。
观察图6可知,在电网出现不平衡故障时,文章所设计的控制系统能够很好的实现控制目标,对于控制目标1能够保持交流输出电流的对称,但此时功率则出现了二倍频波动,分别如图6(a)(2)和图6(a)(3)所示;对于控制目标2而言,当有功功率的二倍频波动被消除之后,MMC交流输出电流明显增加且并不对称输出,分别如图 6(b)(2)和图 6(b)(3)所示;对于两种控制目标下,不平衡故障时直流电压和直流电流均出现了二倍频波动,如图6(4)和图6(5)所示,相比之下控制目标1时直流电压/电流的波动明显大于控制目标2,当在0.6 s时环流抑制控制器启动后直流电压/电流的二倍频波动均被抑制,主要是由于零序环流此时被抑制。
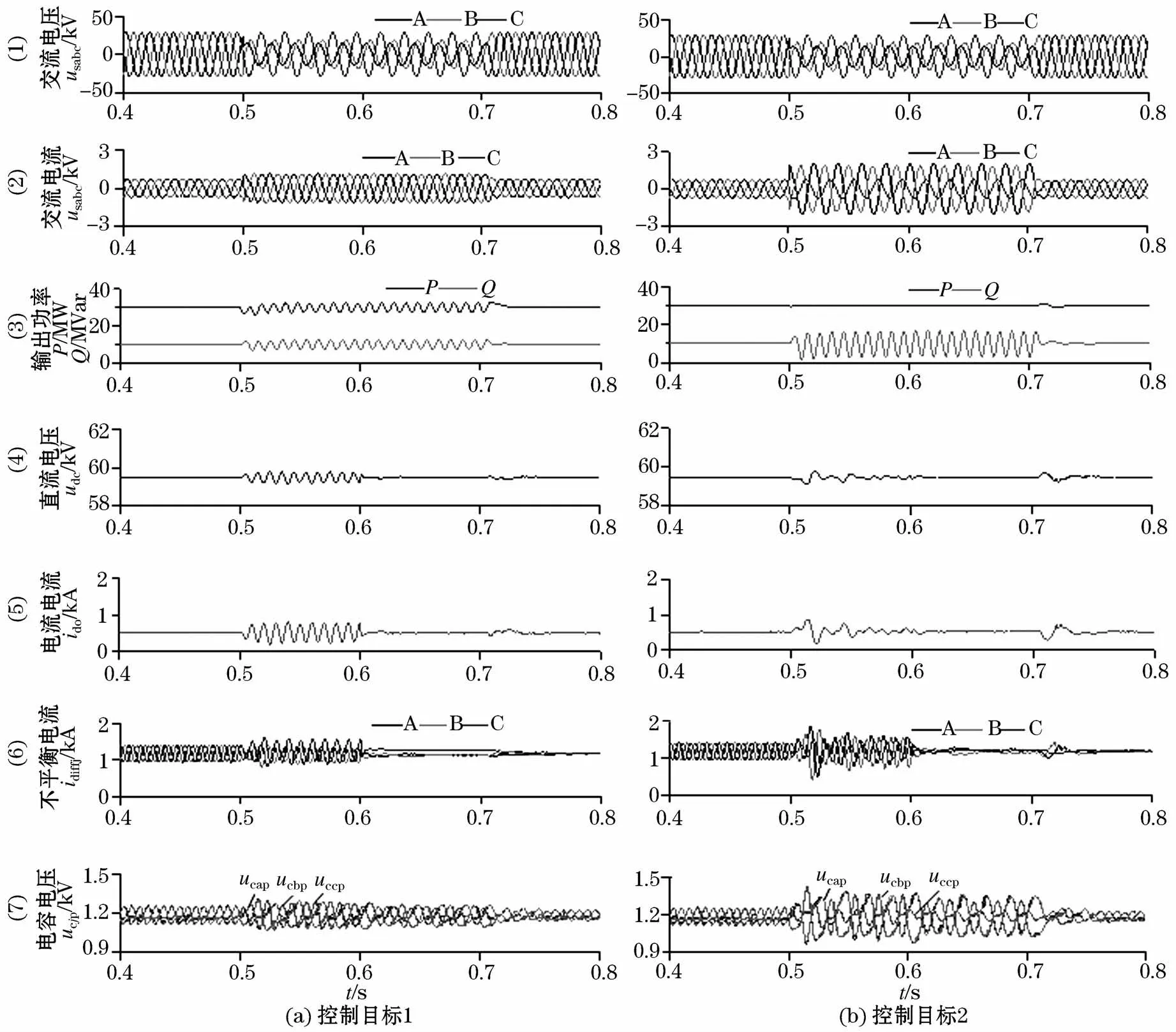
图6 两种不平控制目标的仿真结果Fig.6 Simulation results of two kinds of unbalanced control targets
当电网电压出现不平衡时,在两种控制目标下,MMC内部相间环流增大且不对称,在环流抑制启动后,内部不平衡电流idiffj中的直流成分依然在三相中不均分,如图6(a)(6)和图6(b)(6)所示;此时 MMC各个相单元的子模块电容电压明显比平衡工况下波动更剧烈,如图 6(a)(7)和图 5(b)(7)所示;对比两种控制目标,控制目标2的波动程度明显大于控制目标1,且三相间的不对称度更为明显,A、B两相的电容电压波动程度显然大于C相。电网电压不平衡时,交流电流增大,MMC桥臂电流也将增大,各个子模块所承载的电流将增大,应该采取相应的过电流保护措施,防止换流阀器件被损坏。
图7和图8分别为控制目标1、2时文章提出的控制策略与传统的双电流PI调节方法的结果对比图。如图所示,当MMC运行在平衡和不平衡的稳态时,两种控制策略的效果无论是交流电流还是功率基本相同,并没有太大的区别;但是在暂态过程中,明显文章提出的PROR控制策略下的交流电流和功率波形过渡的更为平滑、系统响应更快,PI控制器下MMC交流电流波形在状态切换的过程中两种目标下均出现了一定超调,功率波形波动更为明显;主要PI控制器的设计需要锁相环完成,在电压在平衡与不平衡状态切换过程中,锁相环将受到一定影响,从而影响PI控制器的相应速度。因此,相比于传统的正、负序电流PI控制策略,文章所提出的控制策略具有一定的优越性。

图7 控制目标1是PROR和PI波形对比Fig.7 Waveform comparison of PROR with PIwhen control target1

图8 控制目标2是PROR和PI波形对比Fig.8 Waveform comparison of PROR with PIwhen control target2
5 结束语
(1)当电网电压出现不平衡故障时,MMC交流系统不再保持对称运行,此时交流输出电流增大、直流侧出现二倍频波动,将影响MMC-HVDC系统的电能传输质量;
(2)MMC内部桥臂电流增大、子模块电容电压波动更为剧烈、相间环流包含正序、负序和零序环流,零序环流进入直流侧引起直流电压/电流二倍频波动,直流电流在三相中不再均分;
(3)在αβ坐标系下建立电网电压不平衡MMC控制系统,引入比例降阶谐振控制器设计电流环和环流抑制控制器;对比与传统的矢量控制策略无需对电流进行正、负序分离,动态响应速度快,且系统无需锁相环,控制系统相对简单,仿真结果验证了所提出的控制策略的有效性。

