低雷诺数下二维翼型层流分离颤振特性
李国俊,白俊强, *,唐长红,刘南,乔磊
1.西北工业大学 航空学院,西安 710072 2.航空工业空气动力研究院,沈阳 110034
低雷诺数下二维翼型层流分离颤振特性
李国俊1,白俊强1, *,唐长红1,刘南2,乔磊1
1.西北工业大学 航空学院,西安 710072 2.航空工业空气动力研究院,沈阳 110034
低雷诺数;转捩;层流分离颤振;湍流;尾涡脱落;非线性
自然界中的飞行生物通过漫长的进化和自然选择过程,形成了各具特色的空中飞行能力,能够在复杂的环境中猎取食物、逃避敌害、生殖繁衍和聚集活动。从古至今,人类从未放弃对飞行的研究,而生物飞行的高机动性、推进高效性、远距离迁徙、低噪声以及飞行的高升阻比等,均是现在人造飞行器所无法比拟的[1]。当前国内外兴起的微小型飞行器研究热潮,正是不断从昆虫、鸟类以及蝙蝠等中小型飞行动物的高效飞行模式中探寻新的设计概念,来提升此类飞行器的飞行性能。大部分的鸟类、昆虫以及微小型飞行器具有体积小、飞行速度低等特点,从而会在低雷诺数条件下飞行。在低雷诺数流动范围内,气体出现复杂的黏性流动现象,例如涡脱落、边界层转捩以及由层流分离和湍流再附形成的分离泡等,这些现象会显著地改变飞行器的气动性能,增强气动力的非线性[2]。同时,研究人员针对转捩流动的动态演化过程进行了深入的研究[3],其复杂的物理机理无疑增加了流固耦合问题分析的难度。此外,部分飞行生物的翅膀和微小型飞行器的机翼具有较大的柔性,容易在气动载荷作用下发生变形,而这种变形又会影响翼面流动,从而形成复杂的流固耦合现象。
早在20世纪50年代,Vooren和Lambourne[4-5]等通过实验发现在低雷诺数范围内存在小振幅的俯仰极限环振荡(LCO)现象,研究结果表明转捩及层流分离流动对该类型振荡的产生至关重要,这与由动态失速导致的失速颤振明显不同,但是缺乏对其诱发机理的深入分析。Shyy等[6]于2008年在其著作中回顾了近几十年来对低雷诺数范围内的复杂流动及流固耦合现象的研究,并指出转捩及层流分离等现象对飞行生物以及人造飞行器的气动性能和飞行稳定性有较为显著的影响,在类似的研究中应对转捩和层流分离等现象加以考虑。
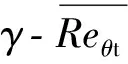
1 流场求解
1.1 非定常气动力求解
本文采用课题组自研的CFD代码——TeAM求解非定常气动力,其控制方程是三维非定常积分形式的Navier-Stokes方程,其直角坐标系的守恒形式积分方程为
(1)
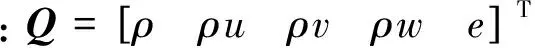
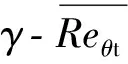
转捩的触发与转捩区发展的预测主要在间歇因子输运方程中完成。该方程由Menter等[16]在2004年提出,Langtry[17]在2006年进行了一些改进,解决了转捩区过短、驻点间歇因子生成项过大等问题。Langtry在2006年给出的间歇因子输运方程为
(2)
式中:γ为间歇因子;ui为当地速度;t为时间;Pγ为生成项;Eγ为耗散项;μ为层流黏性系数;μt为湍流黏性系数;σγ为扩散项系数。若“当地转捩”的判据满足,Pγ启动即γ开始增长,Eγ保证在层流边界层中γ趋近于0,这也为预测再层流化现象提供了条件。
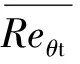
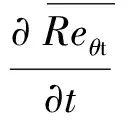
(3)
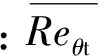
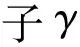
γeff=max(γsep,γ)
(4)
转捩模型通过γeff控制k-ωSST模型中k方程的生成项和耗散项,即
(5)
式中:Pk和Dk分别为原始k方程的生成项和耗散项。
2 结构运动方程
具有俯仰单自由度的二维翼型结构运动方程为
(6)
式中:Iq为二维翼型对刚心的质量惯性矩;Dq为俯仰阻尼;Kq为翼型关于刚心的俯仰刚度;MEA为俯仰力矩;q为俯仰角。
针对上述二维单自由度翼型的结构运动方程,进行无量纲化可得
(7)
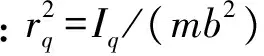
无量纲速度定义为
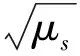
(8)
式中:U∞为自由来流速度;μs=m/(πρ∞b2)为质量比,ρ∞为自由来流密度。
3 气动弹性时域分析流程
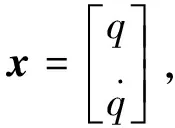
(9)
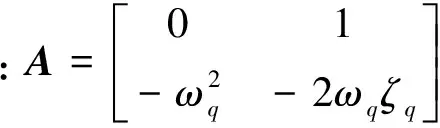
本文采用基于预估-校正技术的四阶隐式Adams线性多步法[18]对式(9)进行时域推进求解,即
预估步:
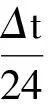
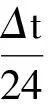
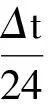
37B·Fn-2-9B·Fn-3)
(10)
校正步:
xn+1=xn+
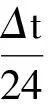
37B·Fn-2-9B·Fn-3)
(11)
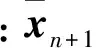
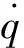
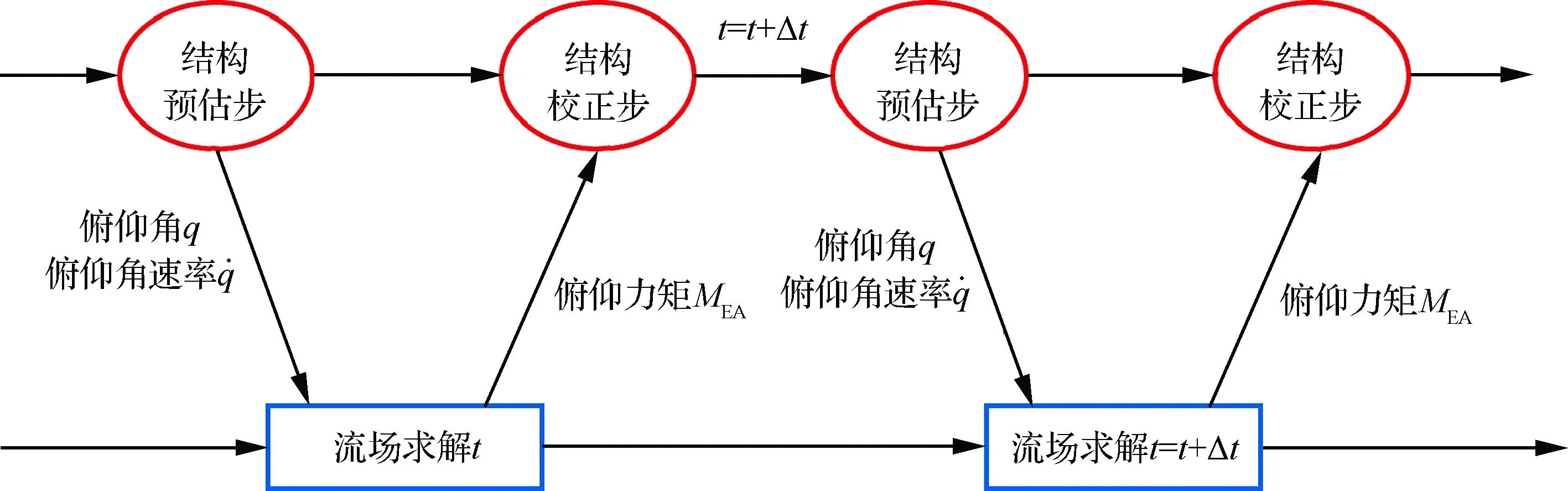
图1 气动弹性时域分析系统的时间推进和数据传递路线Fig.1 Time marching method and data transformation path of time domain aeroelastic analysis system
4 层流分离颤振数值模拟精度验证与分析
4.1 算例说明

图2 层流分离颤振试验[2]Fig.2 Test of laminar separation flutter[2]
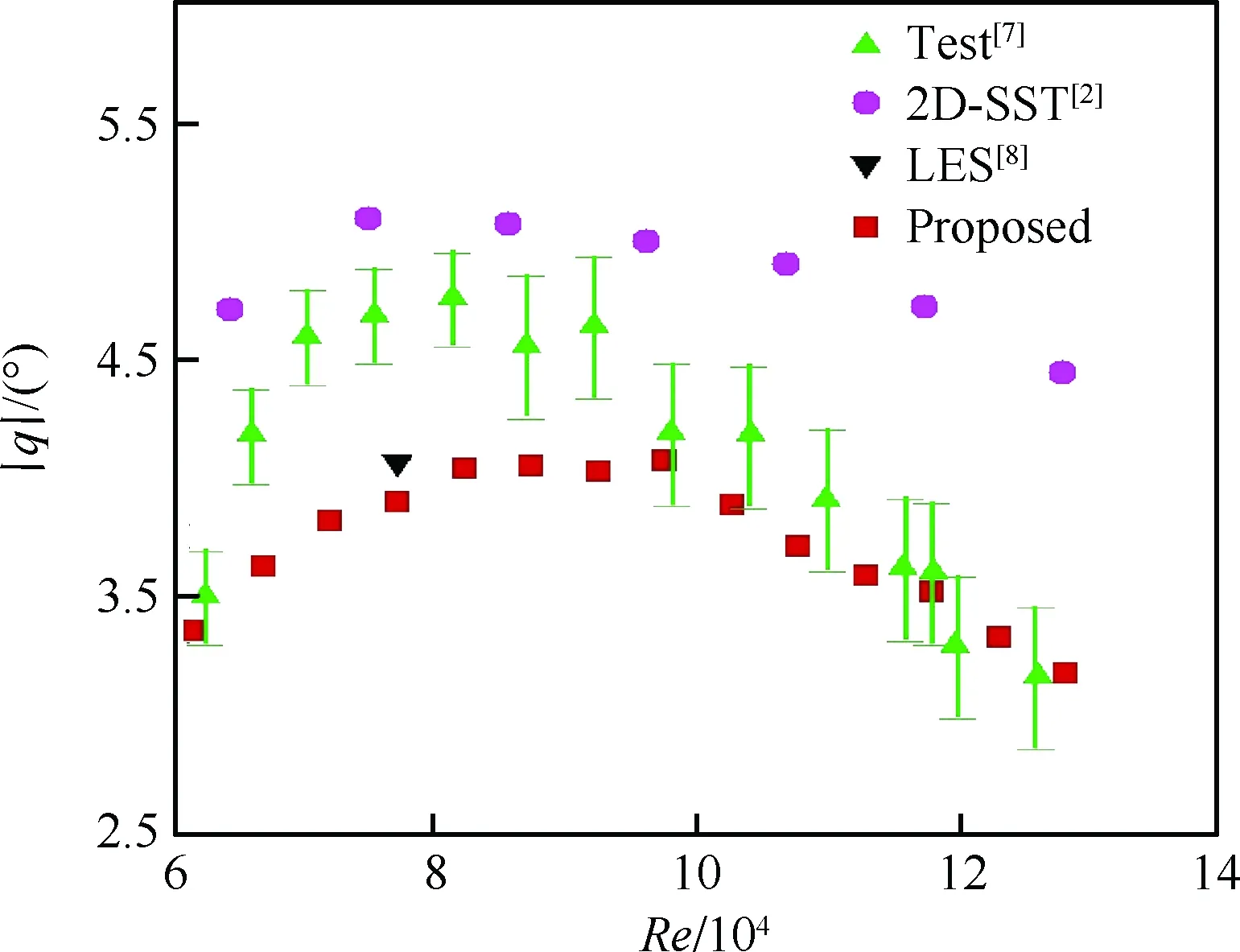
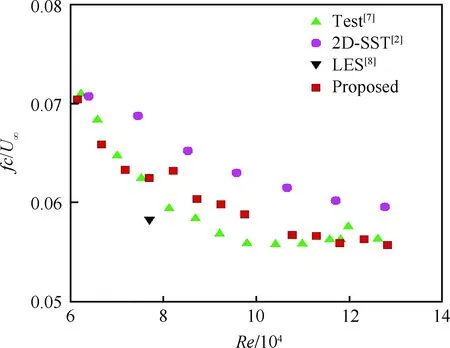
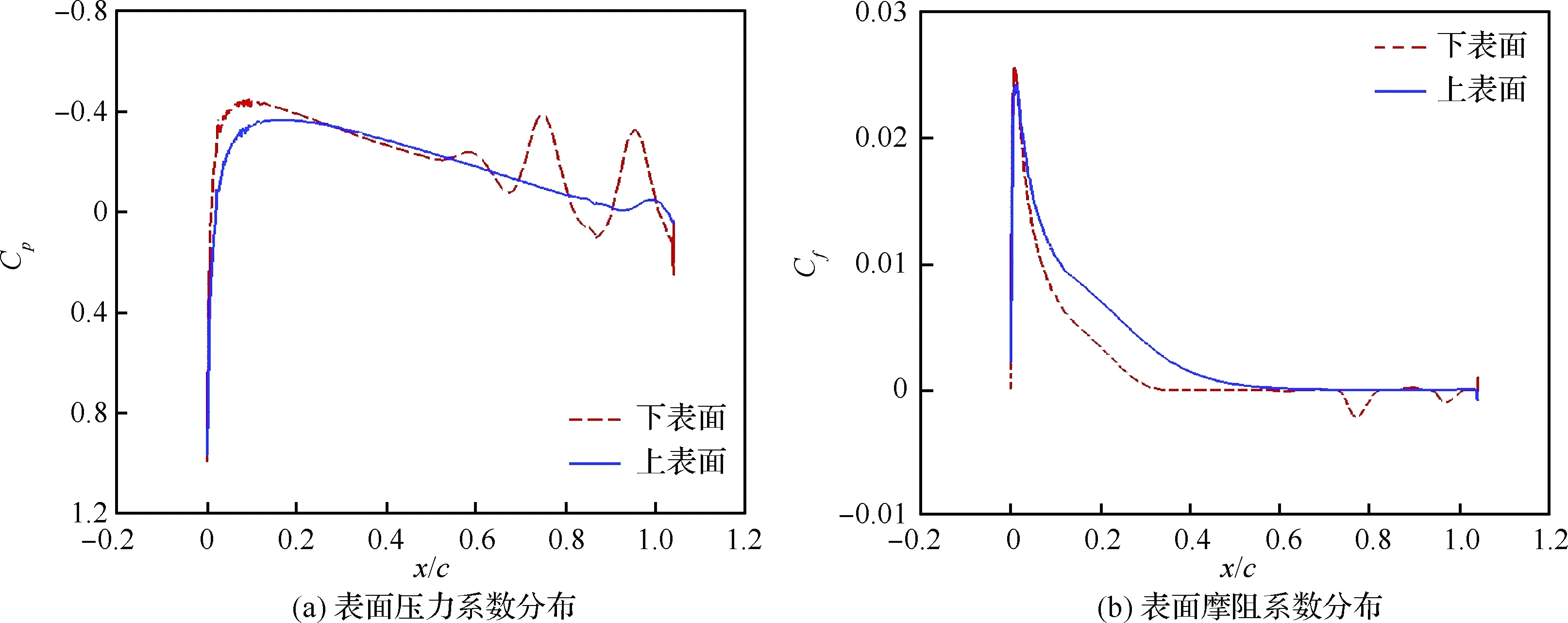
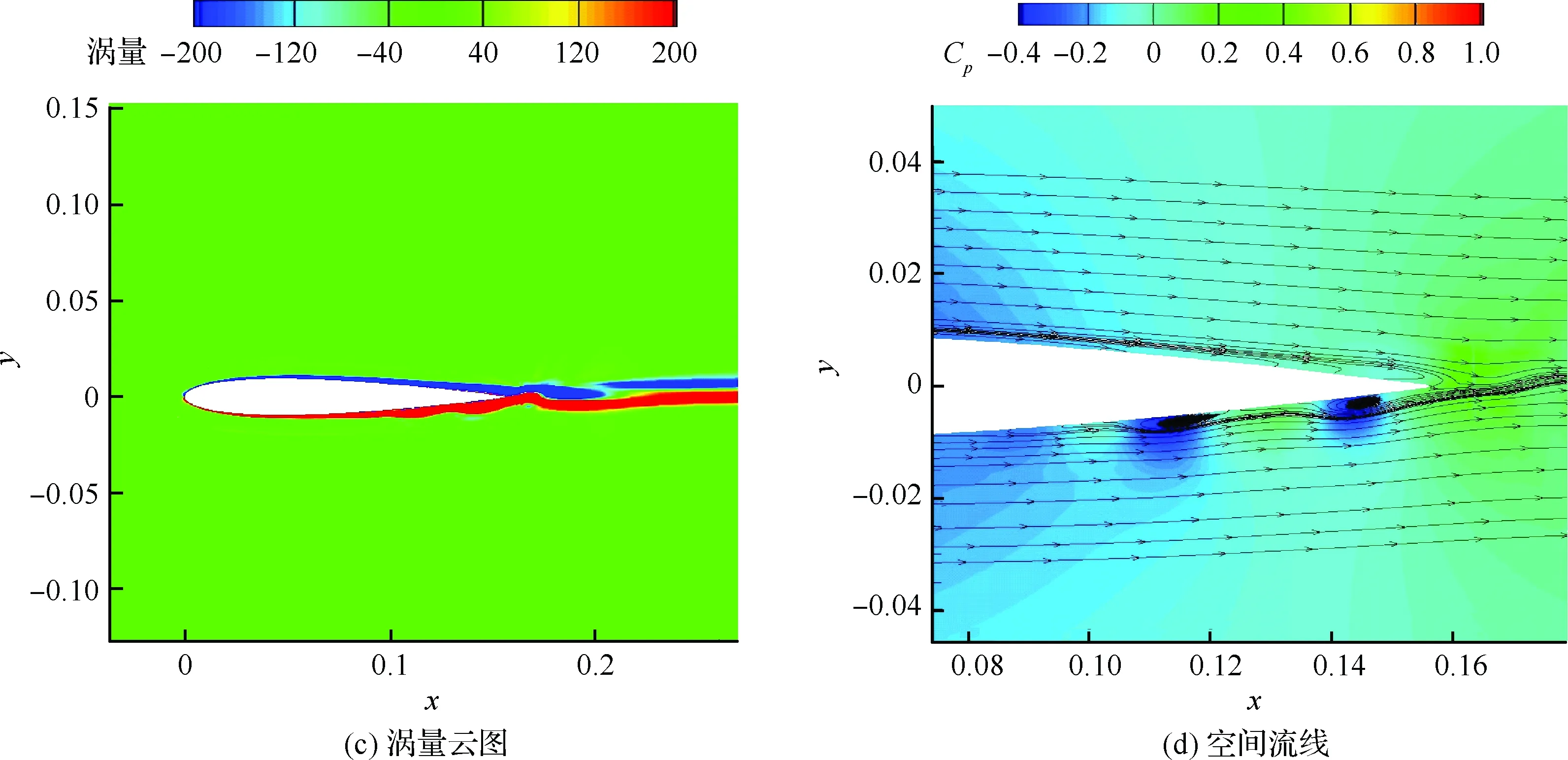
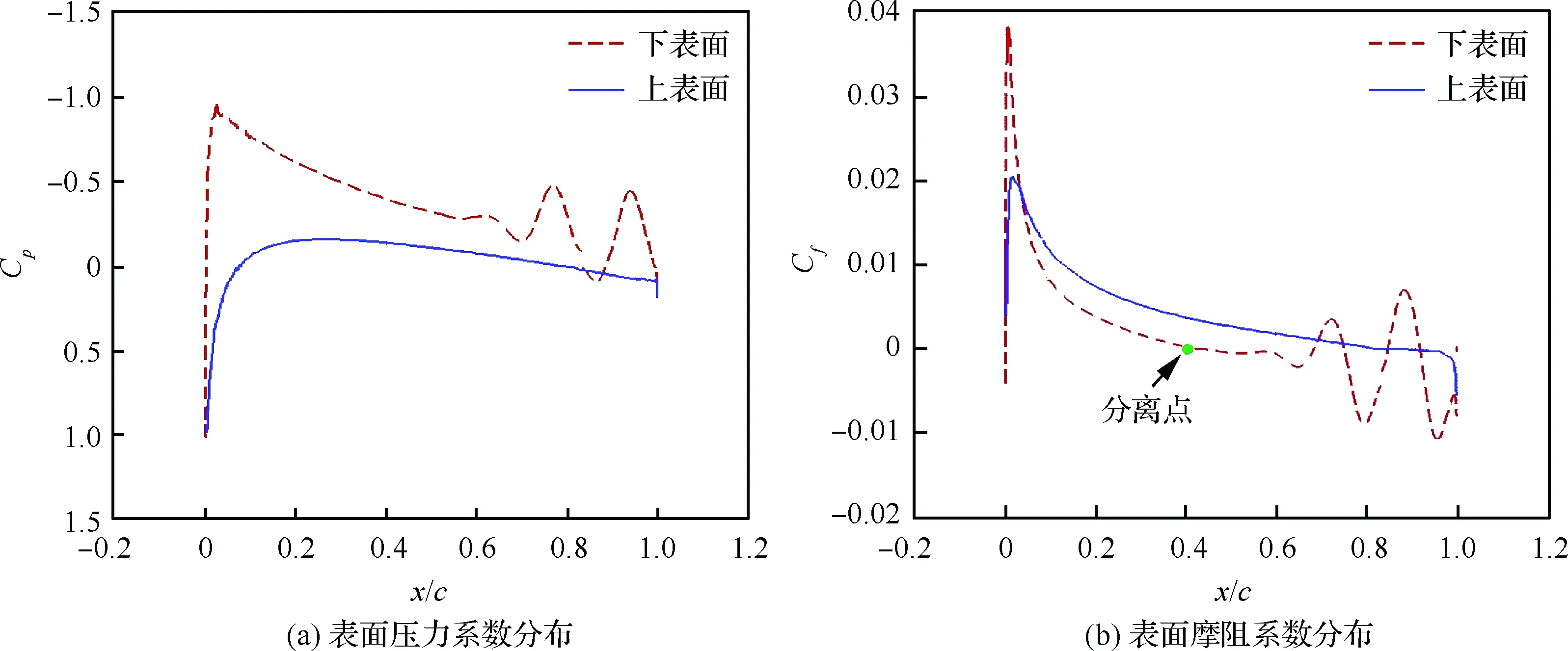
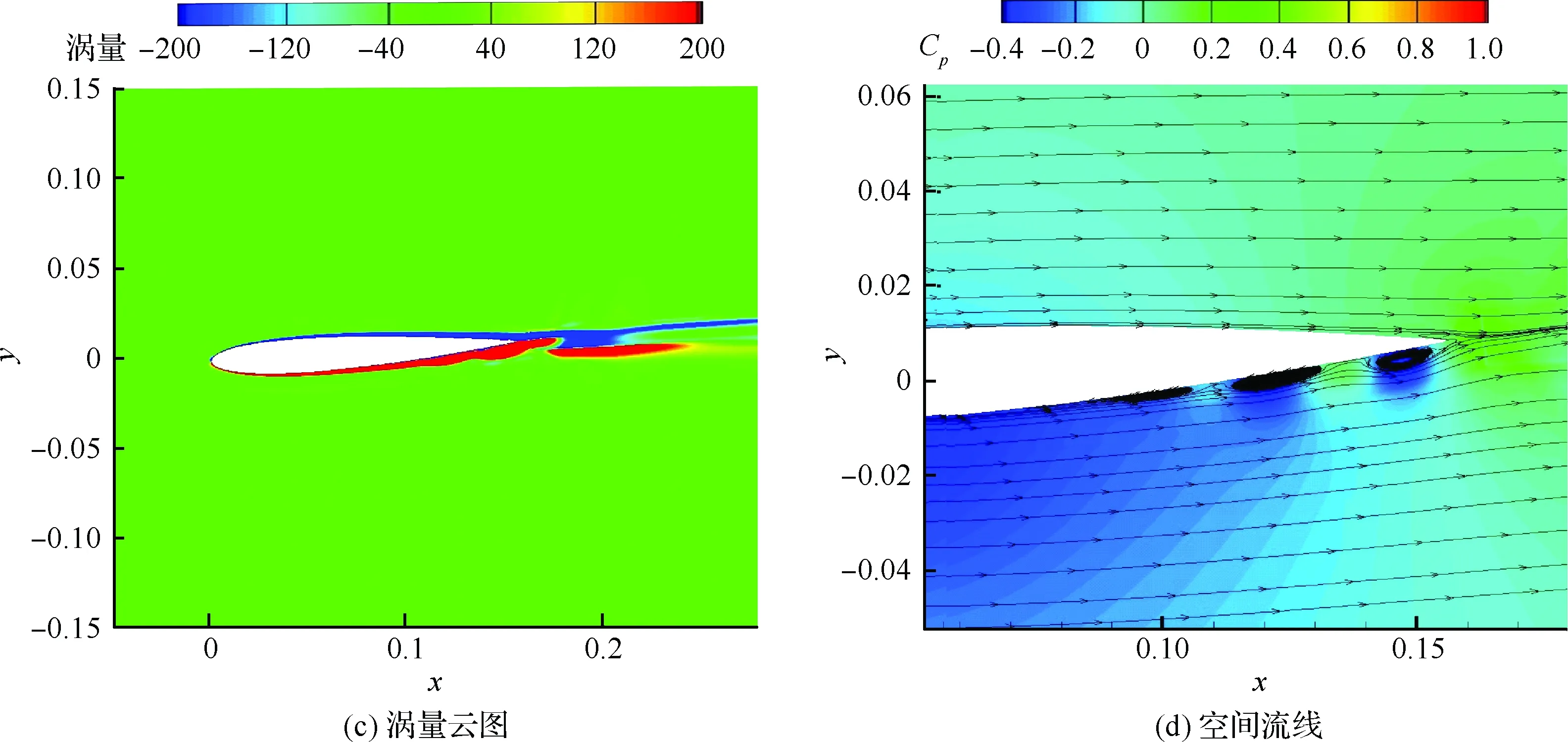
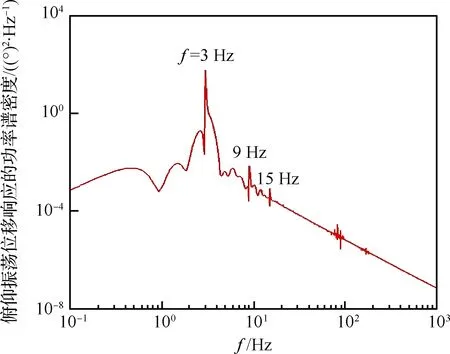
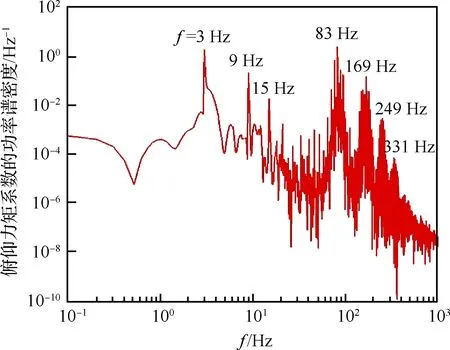
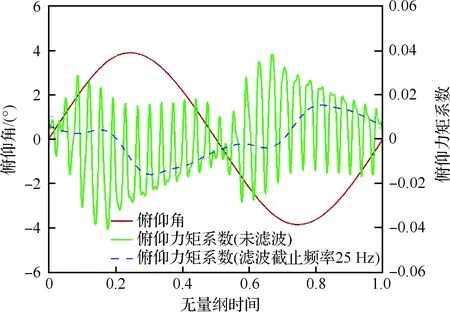
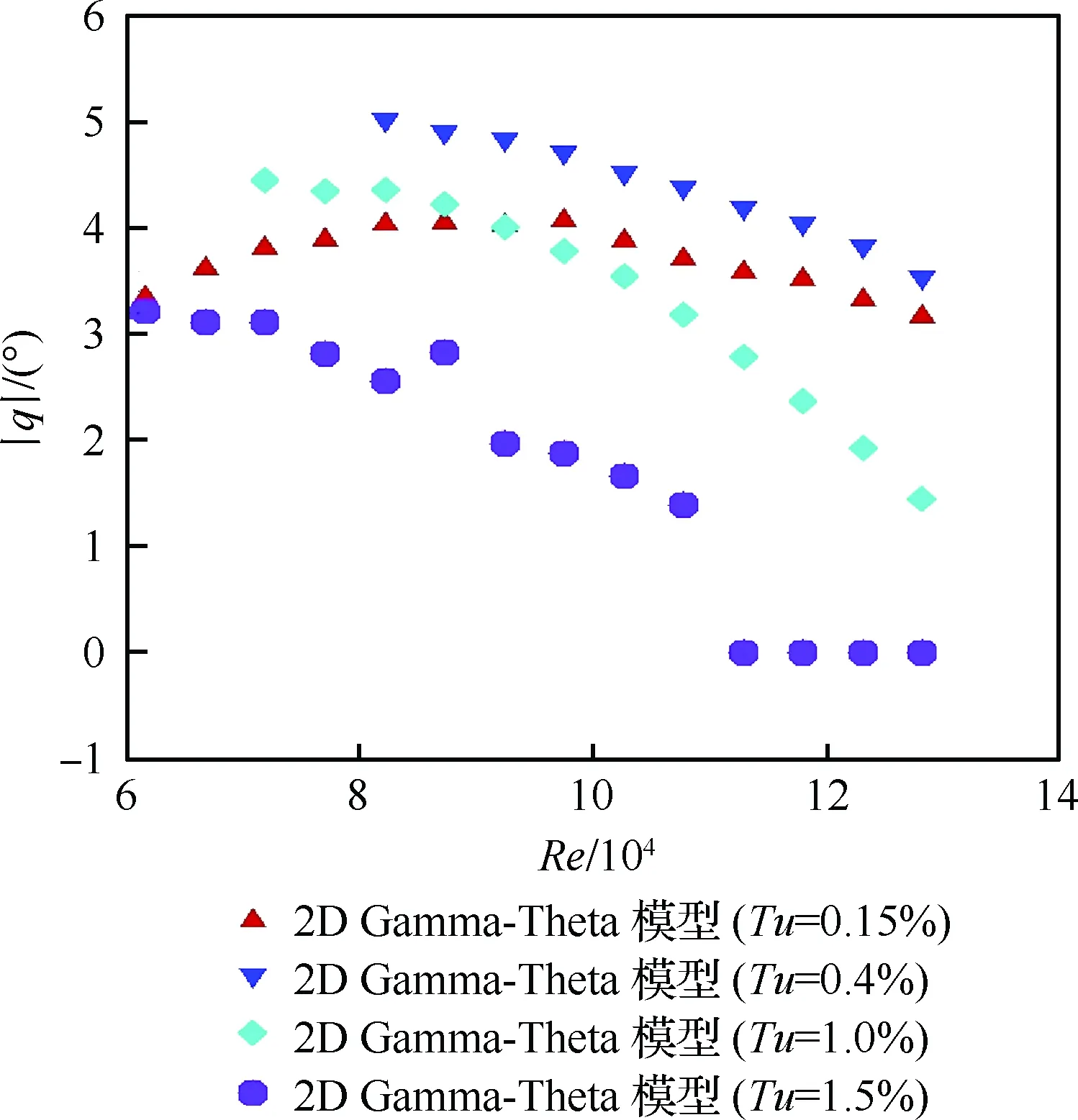
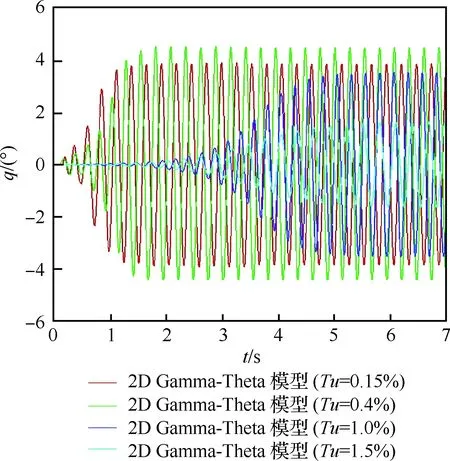
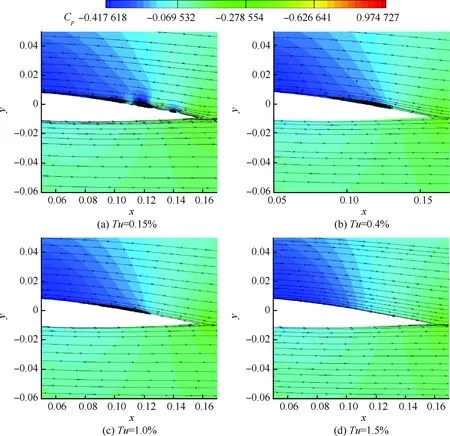
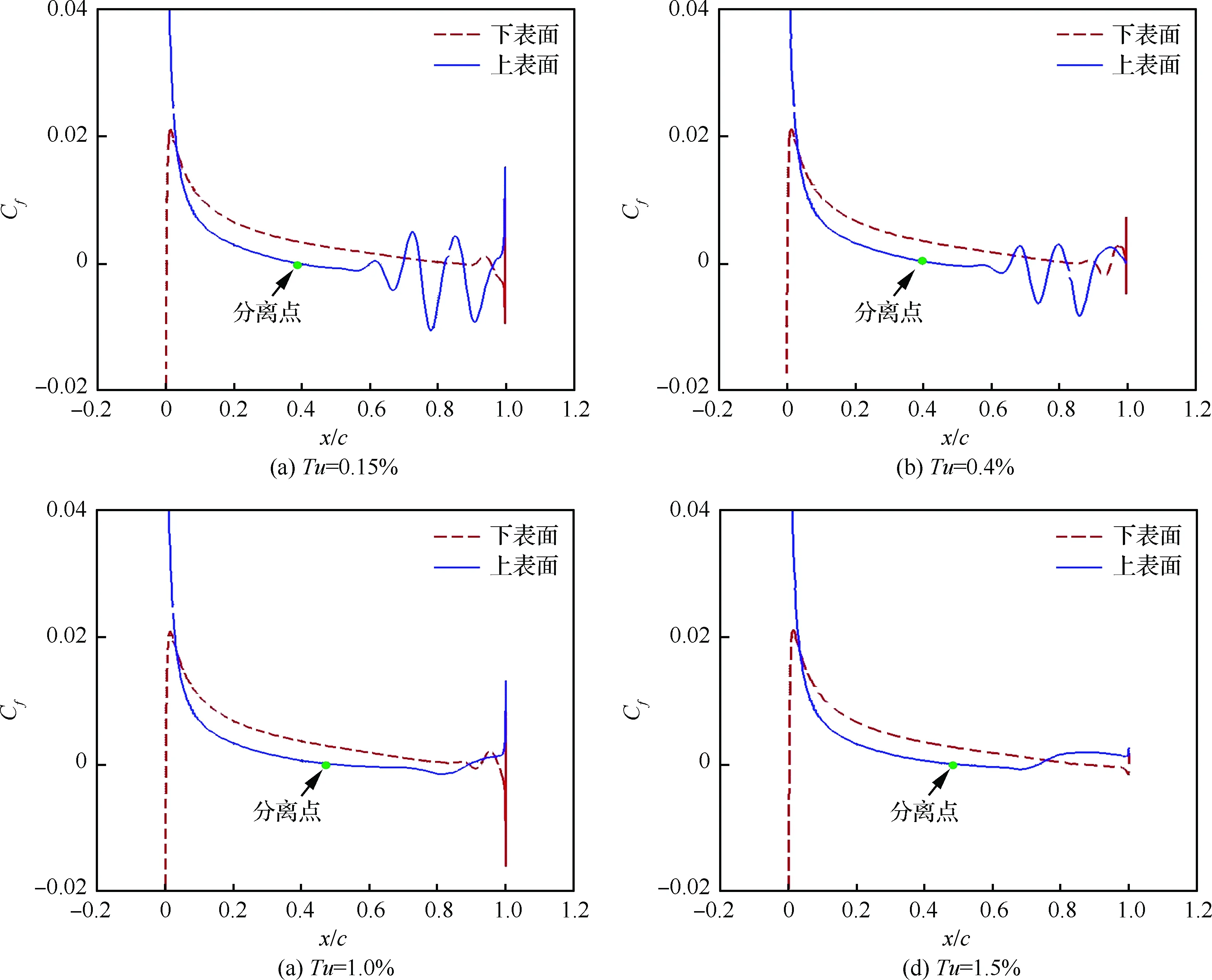
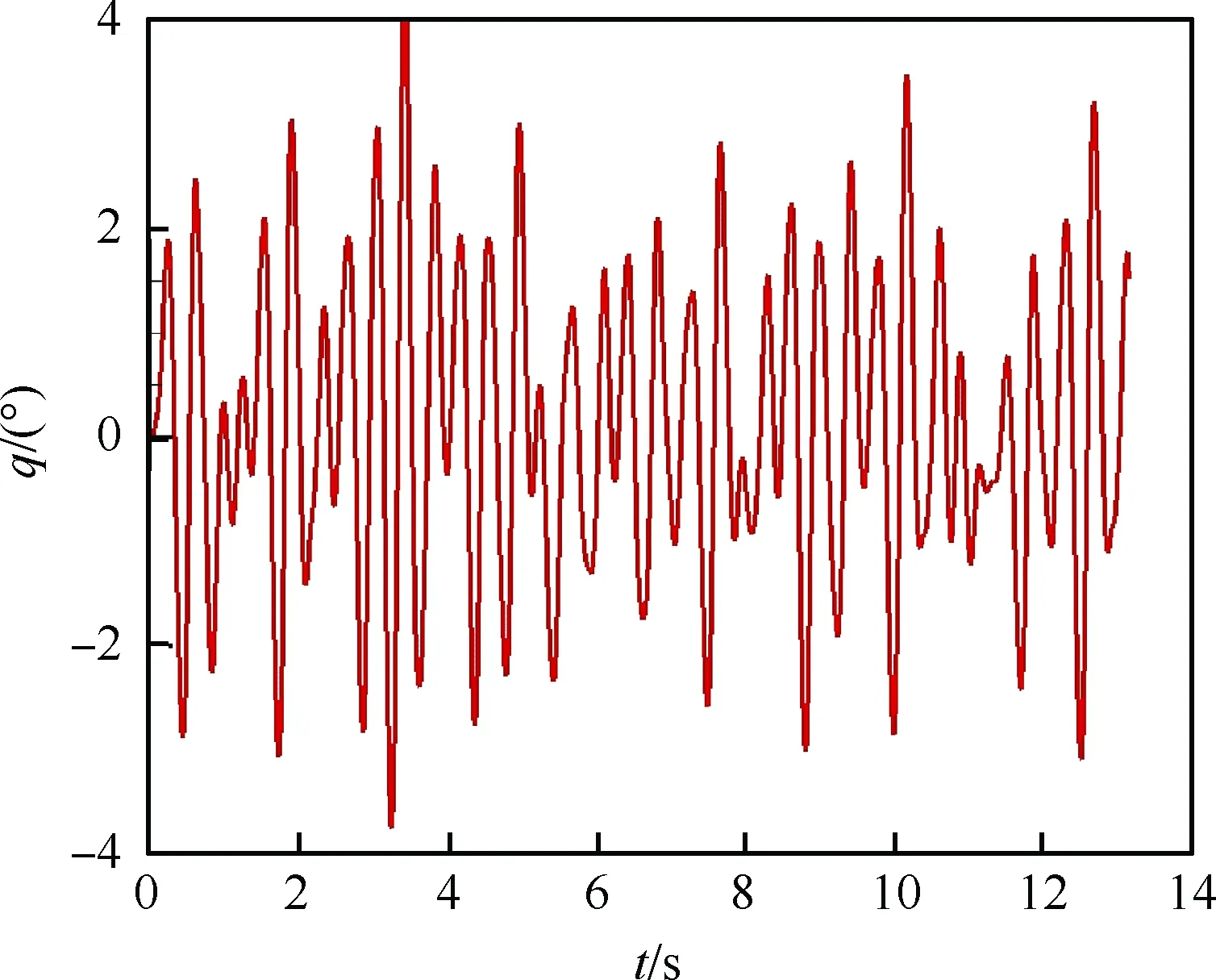
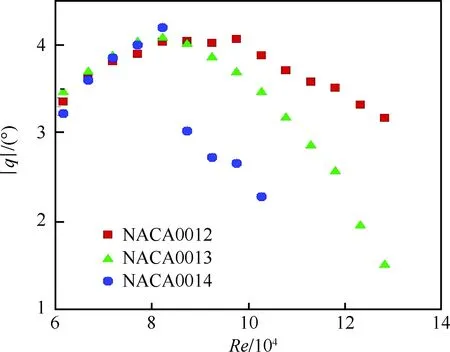
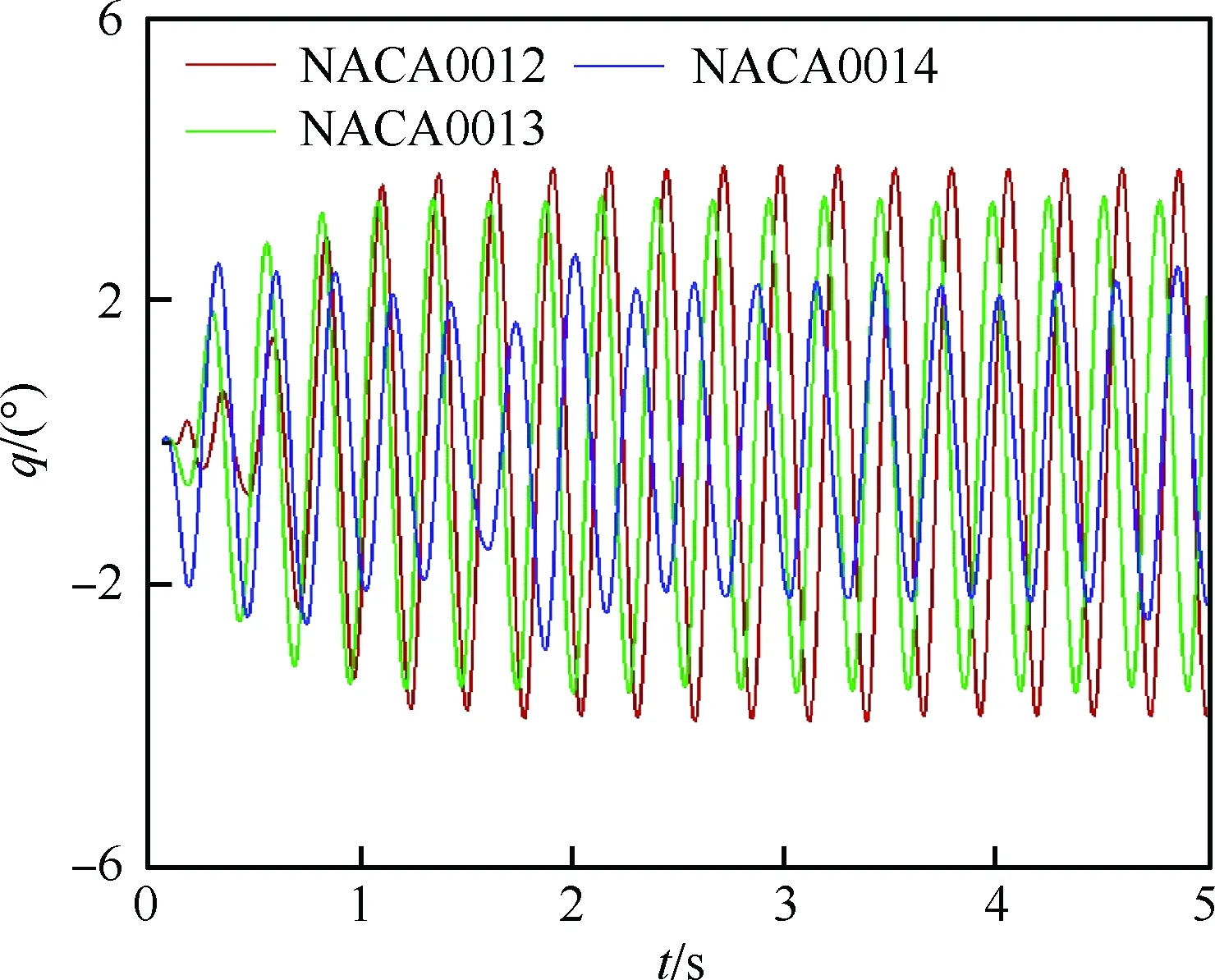
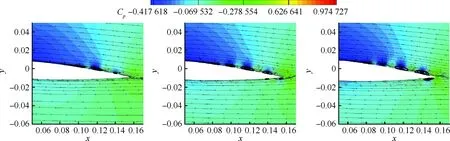
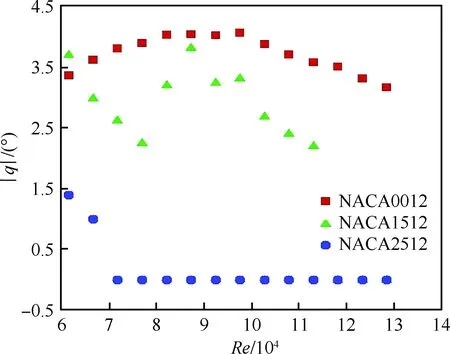
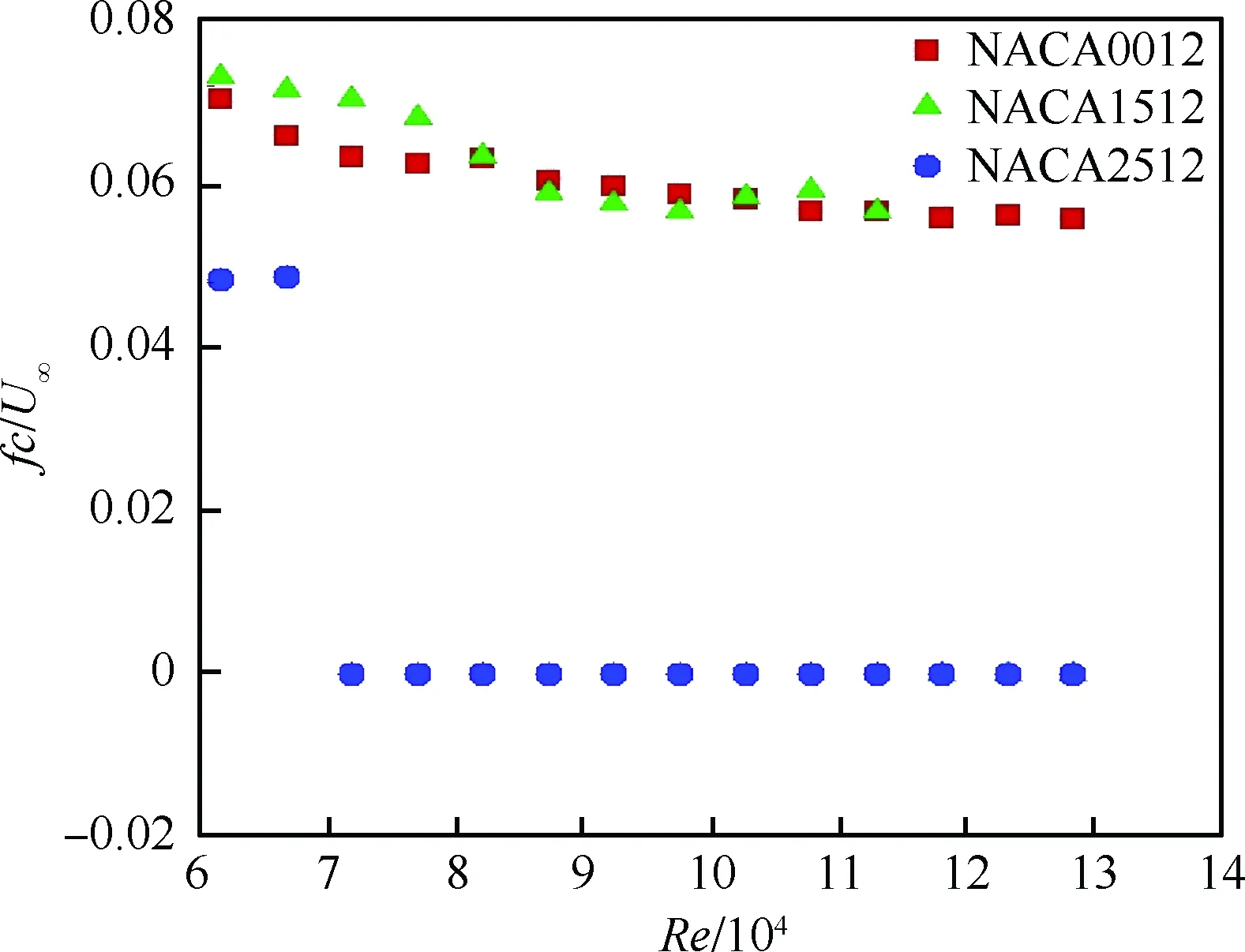
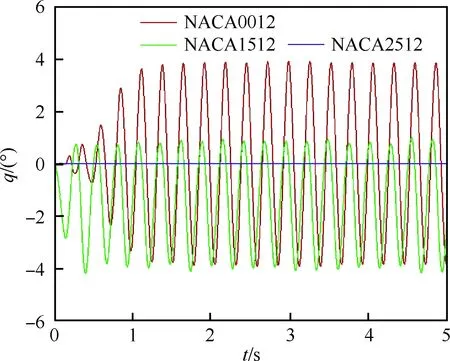
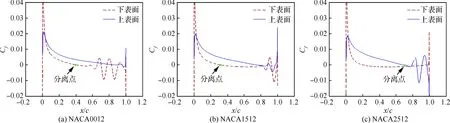
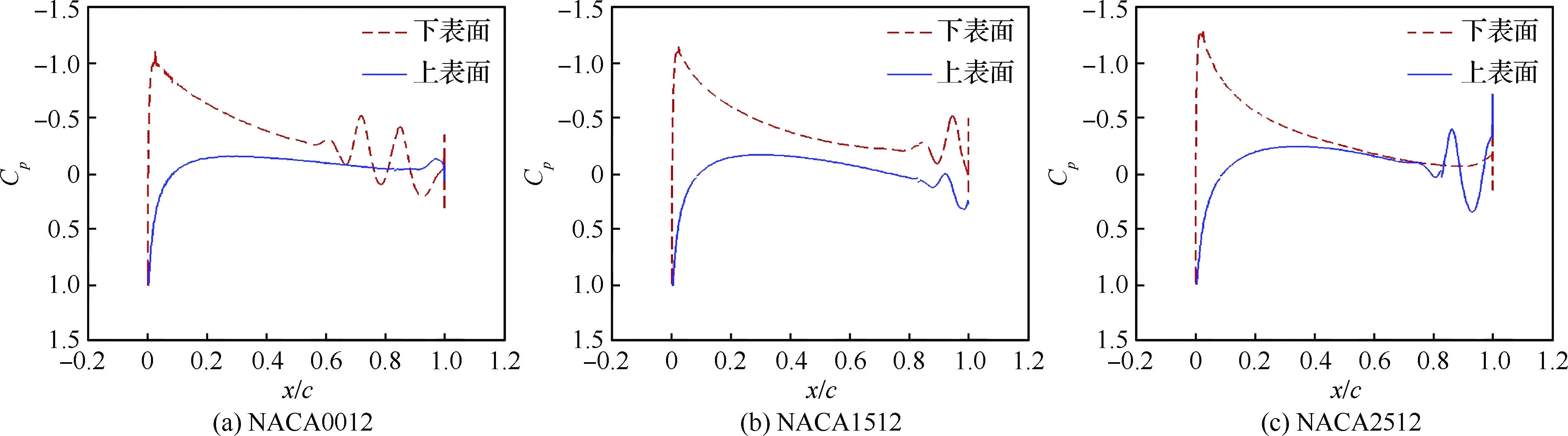
具有俯仰单自由度的NACA0012翼型的层流分离颤振试验[2]是在加拿大皇家军事学院(Royal Military College of Canada) Poirel教授的主持和参与下完成的。Poirel教授课题组对NACA0012翼型在低雷诺数范围内(5.0×104 图3 NACA0012翼型气动弹性模型简图Fig.3 Schematic of aeroelastic model of NACA0012 airfoil 图4 NACA0012翼型计算网格Fig.4 Computational grid of NACA0012 airfoil 图5 层流分离颤振的幅值Fig.5 Amplitudes of laminar separation flutter 图6 层流分离颤振的减缩频率Fig.6 Reduced frequencies of laminar separation flutter 图5和图6分别展示了本文计算得到的层流分离颤振的幅值|q|和减缩频率fc/U∞,并与试验结果[7]、SST湍流模型结合低雷诺数修正的计算结果[2]以及LES方法的数值模拟结果[8]进行对比。Poirel等[7]指出该试验的幅值结果具有一定的测量误差范围:Re<85 000时,误差范围是±0.2°;Re>85 000时,误差范围是±0.3°。图5中三角形两头的竖线表示该处试验值的测量误差范围。对比结果表明,当Re>100 000时,本文计算得到的幅值均处于测量误差范围内,相比于其他方法的计算结果更接近试验值;当Re<100 000时,本文计算得到的幅值小于试验结果,且处于测量误差范围外。值得注意的是,虽然本文计算得到的幅值在Re=77 000时与试验值有一定差别,但是与Wang等[8]采用LES方法计算得到的幅值十分接近。图6结果表明,本文计算得到的振动频率和试验结果吻合很好。 层流分离颤振伴随着边界层转捩、层流分离以及尾涡脱落等复杂黏性流动现象,这些现象会影响层流分离颤振的特性。为了探究上述复杂流动现象对颤振特性的影响,对Re=77 000时的颤振特性以及瞬时流场进行分析。图7和图8分别展示了NACA0012翼型俯仰振荡收敛历史和相平面图。图7结果表明,在无初始扰动的状态下,翼型经过1.5 s的过渡期后进入等幅振荡状态;图8的相平面结果表明,图中曲线存在“波纹”,并非光滑曲线。 图9~图12分别展示了一个完整周期T内在t/T=0,0.25,0.5,0.75时的瞬时流场结果。对比不同时刻翼型表面压力系数Cp分布和表面摩阻系数Cf分布,结合瞬时流场云图可以得知,翼型表面出现了转捩、分离流动、湍流再附以及由此形成的分离泡等复杂流动现象。例如在t/T=0.25时,从图10(b)可以得知在翼型上表面40%弦长处发生分离,随后出现湍流再附现象,并且在翼型表面靠近后缘位置形成多个大小不一的分离泡。 图7 层流分离颤振响应(Re=77 000)Fig.7 Response history of laminar separation flutter(Re=77 000) 图8 相平面图(Re=77 000)Fig.8 Phase plane (Re=77 000) 图9 t/T=0时的瞬时流场结果(Re=77 000)Fig.9 Instantaneous flow field results at t/T=0 (Re=77 000) 图10 t/T=0.25时的瞬时流场结果(Re=77 000)Fig.10 Instantaneous flow field results at t/T=0.25 (Re=77 000) 值得注意的是,在t/T=0和0.5两个时刻,即翼型处于初始平衡位置,从图9和图11可以看出,在对称翼型上下表面靠近后缘位置出现了多个大小不一并且非对称分布的分离泡。此处的压力分布出现了剧烈的抖动,这是由边界层分离导致的高频流动不稳定性引起的。虽然此时翼型处于平衡位置,但是由于此类位于翼型上下表面的非对称分布分离泡的出现以及随后的尾涡脱落,使得对称翼型在平衡位置的压力分布不再对称,导致翼型从平衡位置失稳, 从而诱发层流分离颤振现象。因此可以将这种分离泡的产生及尾涡脱落现象看成是一种扰动。这种扰动持续存在于流场中,所以即使在初始时刻不对对称翼型施加外来扰动,非对称的分离泡和尾涡脱落也可以促使翼型从平衡位置开始失稳振荡直至等幅状态。综合上述分析结果,层流分离是触发层流分离颤振的重要因素。 图11 t/T=0.5时的瞬时流场结果(Re=77 000)Fig.11 Instantaneous flow field results at t/T=0.5 (Re=77 000) 图12 t/T=0.75时的瞬时流场结果(Re=77 000)Fig.12 Instantaneous flow field results at t/T=0.75 (Re=77 000) 为了分析尾涡脱落对颤振特性的影响,对俯仰振荡位移响应和力矩系数响应进行处理,得到各自的功率谱密度(PSD)示意图,分别如图13和图14所示。从图中结果可以看出,翼型俯仰振荡响应和力矩系数响应的主频率为3 Hz,同时还存在许多高频振荡成分。结合图9~图12中的瞬时流场结果可以得知,这些高频振荡与翼型表面的压力分布抖动及高频尾涡脱落密切相关。结合图8中相平面的结果可以得知,曲线的波纹是由边界层分离导致的高频流动不稳定性以及尾涡脱落引起的。 图13 俯仰振荡响应功率谱密度(Re=77 000)Fig.13 PSD of pitching oscillation response (Re=77 000) 图14 力矩系数响应功率谱密度(Re=77 000)Fig.14 PSD of moment coefficients response (Re=77 000) 图15 一个完整周期内的俯仰角和力矩系数 响应曲线(Re=77 000)Fig.15 Pitching displacement and moment coefficient response curves for one cycle (Re=77 000) 图15展示了一个完整周期内的俯仰位移和力矩系数响应曲线(Re=77 000),其中滤波采用切比雪夫滤波器,目的是滤掉由尾涡脱落引起的高频振荡。图中结果表明,滤波前的力矩系数存在不规则的高频振荡,与图14结果一致,这意味着翼型的气动力存在很强的非线性。对一个周期内的翼型俯仰运动和力矩进行积分得到气动力做功,滤波前做功为0.000 449 N·m,滤波后做功为0.000 44 N·m。此时气动力做功为正功,表明翼型从气流中吸收能量。滤波前后气动力做功的对比结果表明,由尾涡脱落引起的力矩系数的高频振荡成分对翼型的气动力做功基本无影响,即高频的尾涡脱落不是维持层流分离颤振的主要因素,仅仅是作为一种对流场的扰动因素,增加了气动力的非线性。 图16 不同湍流度下的振荡幅值Fig.16 Oscillation amplitudes with different turbulent intensities 图17 不同湍流度下的振荡减缩频率Fig.17 Oscillation reduced frequencies with different turbulent intensities 为了探究层流分离和湍流流动对层流分离颤振的影响机制,通过改变来流湍流度Tu获得对应来流条件下的层流分离颤振响应并进行对比,结果如图16和图17所示。从图中结果可以得知,当湍流度从0.15%增加至0.4%时,俯仰振动的幅值略有增大,减缩频率基本无变化。当湍流度继续增大至1.0%时,幅值较0.4%时有所减小,减缩频率则略有增加,但是变化幅度不大。当湍流度增大至1.5%时,幅值随着湍流度的增加继续减小,并且在Re>113 000时不再发生层流分离颤振,幅值为0;减缩频率在Re≤80 000时和湍流度为1.0%的减缩频率基本无差别,当80 000 图18展示了Re=102 670时不同湍流度下的俯仰振荡位移响应,从图中可以看出,随着湍流度增加,俯仰振荡幅值在湍流度为0.4%时达到最大,随后幅值减小。 考虑到在相同的雷诺数下不同来流湍流度对应的俯仰振荡响应幅值不同,因此无法排除瞬时迎角大小对流场结果的影响。为了探究不同湍流度下层流分离以及湍流流动在层流分离颤振中的变化情况,需要对比不同湍流度下翼型的空间流场和表面摩阻系数分布。此处对NACA0012翼型采用相同的强迫运动规律进行研究,主要是为了保证系统仅具有单一的变量——湍流度,可以排除其他变量对流场结果的影响。强迫运动规律为:初始迎角为0°,振幅为4°, 振动频率为3.5 Hz。 图18 不同湍流度下的俯仰振荡响应(Re=102 670)Fig.18 Pitching oscillation response with different turbulent intensities (Re=102 670) 该运动规律接近湍流度为0.15%时在Re=102 670下的层流分离颤振响应。翼型的空间流线和表面摩阻系数分布对比分别如图19和图20所示,此时翼型处于正向最大俯仰位移处。 图19和图20中的结果表明,随着来流湍流度增大,翼型表面的分离泡数目减少,摩阻系数抖动减缓,因此由边界层分离导致的高频流动不稳定性减弱。结合图18的分析结果可以得知,由尾涡脱落带来的初始扰动减弱,使得俯仰振荡从启动至等幅振荡所用时间随着湍流度的增加而增加。另外,当来流湍流度为0.15%时,翼型上表面的层流分离点位于40%弦长处,随着湍流度不断增大,分离点向后缘移动。当湍流度增大至1.5%时,分离点推迟至50%弦长处。因此湍流度的增大可以在一定程度上减弱层流分离。 综合图16中不同湍流度下俯仰振荡响应的对比结果,以及上述分析结论可以得知,当Tu≥0.4%时, 随着湍流度增大, 由层流分离流动和尾涡脱落诱发的翼型表面压力振荡减弱,俯仰振荡幅值减小;当Tu=1.5%时,在部分雷诺数下翼型不再发生层流分离颤振现象;湍流度继续增大至2%以上或在全湍流动下,翼型表面不再出现层流分离,层流分离颤振现象也随之消失。这说明层流分离能够维持层流分离颤振;而湍流流动对俯仰振荡的幅值具有一定程度的抑制作用,对俯仰振荡的减缩频率并无显著影响。 图19 不同湍流度下的空间流线(Re=102 670)Fig.19 Space streamline with different turbulent intensities (Re=102 670) 图20 不同湍流度下的表面摩阻系数分布(Re=102 670)Fig.20 Distribution of surface friction coefficients with different turbulent intensities (Re=102 670) 部分飞行生物和微型飞行器具有主动改变翼型外形的能力,例如翼型的厚度和弯度等,以便适应复杂的飞行环境[19-21]。相应地,此时翼型的气动弹性特性也会发生改变,因此有必要研究翼型外形参数对层流分离颤振特性的影响。 目前Poirel等主要采用NACA0012翼型对层流分离颤振现象开展研究。虽然Yuan[9]对SD7003翼型也进行了数值模拟,但是仅研究了一个来流速度下的翼型振荡特性,缺乏系统性的对比分析。 本节研究了翼型厚度对层流分离颤振的影响,选取的翼型分别为NACA0009、 NACA0012、NACA0013、NACA0014、NACA0016和NACA0018,计算所用的气动参数和结构参数与4.1节中的参数一致。数值模拟结果表明,当翼型为NACA0009时,在初始无扰动情况下,不再发生层流分离颤振;在初始扰动足够大的情况下,翼型在Re=66 733时发生小幅极限环振荡,振幅约为0.5°。当翼型为NACA0016和NACA0018时,翼型在给定雷诺数范围内均发生无规则振荡,与NACA0012翼型的周期性振荡响应有明显区别。其中NACA0016翼型在Re=66 733时的俯仰振荡历史如图21所示。NACA0014翼型在部分雷诺数条件下也会发生类似的不规则振荡。 图21 NACA0016翼型的层流分离颤振 响应(Re=66 733)Fig.21 Response history of laminar separation flutter of NACA0016 airfoil (Re=66 733) 图22 不同厚度翼型的层流分离颤振幅值对比Fig.22 Comparison of amplitudes of laminar separation flutter of airfoils with different thicknesses 图23 不同厚度翼型的层流分离颤振减缩频率对比Fig.23 Comparison of reduced frequencies of laminar separation flutter of airfoils with different thicknesses 图22和图23仅展示了可以发生周期性等幅振荡的NACA0012、NACA0013和NACA0014翼型的振荡幅值和减缩频率。从图中对比结果可以看出,当Re<82 133时,3个翼型的振幅差别不大;当Re>82 133时,随着翼型厚度的增加,俯仰振幅减小。相比之下,3个翼型的减缩频率差别较小。 图24展示了NACA0012、NACA0013和NACA0014翼型在Re=102 670时的俯仰振荡响应,从图中可以看出,随着翼型厚度增加,俯仰振荡响应的幅值减小,但是从初始位置到达等幅振荡状态的过渡时间缩短。 图24 不同厚度翼型的俯仰振荡响应(Re=102 670)Fig.24 Pitching oscillate response of airfoils with different thicknesses (Re=102 670) 采用和5.1节相同的分析方法,对3个不同厚度的翼型给定相同的强迫运动规律,对比分析其在正向最大俯仰位移处的空间流线和表面摩阻系数分布,结果如图25和图26所示。从图中可以得知,随着翼型厚度增大,翼型表面的摩阻系数抖动略有增强,即初始扰动增强,导致过渡时间缩短。另外,翼型厚度增加,使得翼型表面靠近后缘处的流场发生改变,与结构发生耦合后,导致层流分离颤振特性改变。 本节研究了翼型弯度对层流分离颤振的影响,选取的翼型分别为NACA0012、NACA1512和NACA2512,气动参数和结构参数与4.1节中的参数一致。3个翼型的幅值和减缩频率对比分别如图27和图28所示。从图中的对比结果可以看出,随着翼型弯度增加,俯仰振荡幅值减小。对比3个翼型的减缩频率,NACA1512和NACA0012翼型的频率在Re<118 070时相差不大,而NACA2512翼型的减缩频率远小于其他两个翼型。值得注意的是,当Re≥118 070时,NACA1512翼型不再发生振荡;当Re≥71 867时,NACA2512翼型也不再发生振荡,此时这两个翼型的振幅和频率均为0。 图25 不同厚度翼型的空间流线(Re=102 670)Fig.25 Space streamline of airfoils with different thicknesses (Re=102 670) 图26 不同厚度翼型的表面摩阻系数分布(Re=102 670)Fig.26 Distribution of surface friction coefficients of airfoils with different thicknesses (Re=102 670) 图27 不同弯度翼型的层流分离颤振幅值对比Fig.27 Comparison of amplitudes of laminar separation flutter of airfoils with different cambers 图28 不同弯度翼型的层流分离颤振减缩频率对比Fig.28 Comparison of reduced frequencies of laminar separation flutter of airfoils with different cambers 图29展示了NACA0012、NACA1512和NACA2512翼型在Re=102 670时的俯仰振荡响应, 从图中可以看出,随着翼型弯度增加, 俯仰振荡响应的幅值减小,NACA2512此时不发生俯仰振荡。对比NACA0012和NACA1512的俯仰振荡响应,发现NACA1512从初始位置失稳后很快达到等幅振荡状态,所需过渡时间远小于NACA0012翼型,且因为弯度的影响,导致NACA1512的俯仰振荡响应不再以初始位置为基准呈现对称状态。 图29 不同弯度翼型的俯仰振荡响应(Re=102 670)Fig.29 Pitching response of airfoils with different cambers (Re=102 670) 采用和5.1节相同的分析方法,对3个不同弯度的翼型给定相同的强迫运动规律,对比分析其在正向和负向最大俯仰位移处的空间流线、表面摩阻系数分布和表面压力系数分布,结果如图30~图35所示。从图中结果可以得知:NACA0012翼型在正向最大俯仰位移处和负向最大俯仰位移处的空间流线基本是对称的,而NACA1512和NACA2512等带弯度翼型的流线结果明显呈现出非对称性,因此翼型受到的扰动是非对称的,导致其俯仰振荡响应不再对称;当翼型处于正向最大俯仰位移处,随着翼型弯度增加,翼型上表面靠近后缘位置的压力和摩阻系数抖动增强;当翼型处于负向最大俯仰位移处,随着翼型弯度增加,翼型下表面靠近后缘位置的压力和摩阻系数抖动减弱。值得注意的是,在负向最大俯仰位移处, NACA2512翼型下表面没有大的分离泡出现,而是转移到了上翼面,与NACA0012翼型的结果有明显区别。 图30 不同弯度翼型在正向最大俯仰位移处的空间流线(Re=102 670)Fig.30 Space streamline of airfoils with different cambers at the positive maximum pitching displacement (Re=102 670) 图31 不同弯度翼型在正向最大俯仰位移处的表面摩阻系数分布(Re=102 670)Fig.31 Surface friction coefficients of airfoils with different cambers at the positive maximum pitching displacement (Re=102 670) 图32 不同弯度翼型在正向最大俯仰位移处的表面压力系数分布(Re=102 670)Fig.32 Distributions of surface pressure coefficients of airfoils with different cambers at the positive maximum pitching displacement (Re=102 670) 图33 不同弯度翼型在负向最大俯仰位移处的空间流线(Re=102 670)Fig.33 Space streamline of airfoils with different cambers at the negative maximum pitching displacement (Re=102 670) 图34 不同弯度翼型在负向最大俯仰位移处的表面摩阻系数分布(Re=102 670)Fig.34 Distributions of surface friction coefficients of airfoils with different cambers at the negative maximum pitching displacement (Re=102 670) 图35 不同弯度翼型在负向最大俯仰位移处的表面压力系数分布(Re=102 670)Fig.35 Distribution of surface pressure coefficients of airfoils with different cambers at the negative maximum pitching displacement (Re=102 670) 1) 本文建立的具有转捩预测能力的时域气动弹性数值模拟方法可以准确地模拟NACA0012翼型的层流分离颤振现象。 2) 在翼型上下表面靠近后缘位置出现了多个非对称分布的分离泡,导致此处的翼型表面压力分布发生了剧烈的抖动。这种分离泡的产生及尾涡脱落现象相当于一种扰动,迫使翼型从平衡位置失稳,从而发生层流分离颤振现象。这些复杂黏性流动现象的出现与层流分离密切相关,因此层流分离是触发层流分离颤振的重要因素。 3) 通过滤波器过滤掉层流分离颤振中的高频振荡成分,发现滤波前后的气动力做功基本无变化,这说明高频的尾涡脱落不是维持层流分离颤振的主要因素,仅仅是作为一种对流场扰动的因素,增加了气动力的非线性。 4) 通过对不同湍流度下NACA0012翼型的层流分离颤振响应进行对比分析,发现层流分离能够维持层流分离颤振,而湍流对俯仰振荡幅值具有一定程度的抑制作用,对俯仰振荡的减缩频率并无显著影响。通过对具有不同厚度和弯度的翼型进行数值模拟,对比其层流分离颤振响应,发现适当地减小翼型厚度或者增大翼型弯度,可以完全避免层流分离颤振的发生;而增大翼型厚度,虽然其振荡幅值减小,但是难以完全避免层流分离颤振,甚至在部分工况下出现不规则振荡。 综上所述,转捩、层流分离、湍流流动以及分离泡等复杂黏性流动现象密切相关,从而会间接影响层流分离颤振特性。所以转捩和层流分离预测的精准与否在层流分离颤振研究中至关重要。为了达到抑制甚至消除层流分离颤振的目的,可以适当增大来流湍流度或者采用某种技术手段使机翼表面维持全湍流动,以便获得良好的飞行品质。对于某些飞行生物和具有主动变形能力的飞行器来说,可以通过适当地减小翼型厚度或者增大翼型弯度来避免层流分离颤振的发生,提高对飞行环境的适应能力。 [1] 田方宝. 模拟生物运动的流固耦合数值研究[D]. 合肥: 中国科学技术大学, 2011: 1-5. TIAN F B. Numerical investigation of bio-inspired flow-structure interaction[D]. Hefei: University of Science and Technology of China, 2011: 1-5 (in Chinese). [2] POIREL D, METIVIER V, DUMAS G. Computational aeroelastic simulations of self-sustained pitch oscillations of a NACA0012 at transitional Reynolds numbers[J]. Journal of Fluids and Structures, 2011, 27(8): 1262-1277. [3] LEE C B, WU J Z. Transition in wall-bounded flows[J]. Applied Mechanics Reviews, 2008, 61(3): 1-21. [4] VAN DE VOOREN A I, BERGH H. Spontaneous oscillations of an aerofoil due to instability of the laminar boundary layer[R]. Amsterdam: National Luchtvaart Laboratorium, 1951. [5] LAMBOURNE N C. An experimental investigation on the flutter characteristics of a model flying wing[R]. London: Her Majesty’s Stationery Office, 1952. [6] SHYY W, LIAN Y S, TANG J, et al. Aerodynamics of low Reynolds number flyers[M]. Cambridge: Cambridge University Press, 2008: 29-45. [7] POIREL D, HARRIS Y, BENAISSA A. Self-sustained aeroelastic oscillations of a NACA0012 airfoil at low-to-moderate Reynolds numbers[J]. Journal of Fluids and Structures, 2008, 24(5):700-719. [8] WANG B Y, POIREL D, YUAN W X, et al. Numerical simulation of self-sustained oscillations of an airfoil at a transitional Reynolds number using high-order schemes:AIAA-2011-2139[R]. Reston, VA: AIAA, 2011. [9] YUAN W X, POIREL D, WANG B Y, et al. Simulation of airfoil limit-cycle oscillations of transitional Reynolds numbers: AIAA-2012-0041[R]. Reston, VA: AIAA, 2012. [10] YUAN W X, POIREL D, WANG B Y. Simulations of pitch-heave limit-cycle oscillations at a transitional Reynolds number[J]. AIAA Journal, 2013, 51(7): 1-17. [11] METIVIER V, DUMAS G, POIREL D. Aeroelastic dynamics of a NACA 0012 airfoil at transitional Reynolds numbers[C]∥AIAA Fluid Dynamics Conference. Reston, VA: AIAA, 2013. [12] LAPOINTE S, DUMAS G. Improved numerical simulations of self-sustained oscillations of a NACA0012 with transition modeling[C]∥AIAA Fluid Dynamics Conference & Exhibit. Reston, VA: AIAA, 2013. [13] 吴钦,王国玉,黄彪. 绕振荡水翼流动及其转捩特性的数值计算研究[J]. 力学学报, 2014, 46(1): 1-10. WU Q, WANG G Y, HUANG B. Numerical methods and transition investigation of transient flows around a pitching hydrofoil[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(1): 1-10 (in Chinese). [14] YUAN W X, POIREL D, WANG B Y, et al. Effect of freestream turbulence on airfoil limit-cycle oscillations at transitional Reynolds numbers[J]. Journal of Aircraft, 2015, 52(4): 1-12. [15] 乔磊. 考虑转捩判定的分离流动数值模拟研究[D]. 西安:西北工业大学,2013: 1-20. QIAO L. Numerical simualtion of separation flow incorporating transition modeling[D]. Xi’an: Northwestern Polytechnical University, 2013: 1-20 (in Chinese). [16] MENTER F R, LANGTRY R B, LIKKI S R, et al. Correlation-based transition model using local variables, Part I-Model Formulation[C]∥Proceedings of ASME Turbo Expo 2004, Power for Land, Sea, and Air. New York: ASME, 2004. [17] LANGTRY R B. A correlation-based transition model using local variables for unstructured parallelized CFD codes[D]. Stuttgart: University Stuttgart, 2006: 1-80. [18] 叶正寅, 张伟伟, 史爱明, 等. 流固耦合力学基础及其应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2010:171-173. YE Z Y, ZHANG W W, SHI A M, et al. Fundamentals of fluid-structure coupling and its application[M]. Harbin: Harbin Institute of Technology Press, 2010:171-173 (in Chinese). [19] MOHAMMED A A, WAQAR A, ERWIN S, et al. A review on aerodynamics of non-flapping bird wings[J]. Journal of Aerospace Technology & Management, 2016, 8(1): 8-17. [20] SHYY W, LIAN Y, TANG J, et al. Computational aerodynamics of low Reynolds number plunging, pitching and flexible wings for MAV applications[J]. Acta Mechanica Sinica, 2008, 24(4): 351-373. [21] 杨文青, 宋笔锋, 宋文萍, 等. 仿生微型扑翼飞行器中的空气动力学问题研究进展与挑战[J]. 实验流体力学, 2015, 29(3): 1-10. YANG W Q, SONG B F, SONG W P, et al. The progress and challenges of aerodynamics in the bionic flapping-wing micro air vehicle[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(3): 1-10 (in Chinese). Characteristicsoflaminarseparationflutteroftwo-dimensionalairfoilsatlowReynoldsnumbers LIGuojun1,BAIJunqiang1, *,TANGChanghong1,LIUNan2,QIAOLei1 1.SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.AVICAerodynamicsResearchInstitute,Shenyang110034,China lowReynoldsnumber;transition;laminarseparationflutter;turbulence;trailingvortexshedding;nonlinearity 2017-03-27;Revised2017-06-02;Accepted2017-06-19;Publishedonline2017-06-231024 URL:http://hkxb.buaa.edu.cn/CN/html/20171107.html NationalBasicResearchProgramofChina(2014CB744804) .E-mailjunqiang@nwpu.edu.cn http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2017.121280 V211.47 A 1000-6893(2017)11-121280-19 2017-03-27;退修日期2017-06-02;录用日期2017-06-19;< class="emphasis_bold">网络出版时间 时间:2017-06-231024 http://hkxb.buaa.edu.cn/CN/html/20171107.html 国家“973”计划(2014CB744804) .E-mailjunqiang@nwpu.edu.cn 李国俊,白俊强,唐长红,等.低雷诺数下二维翼型层流分离颤振特性J.航空学报,2017,38(11):121280.LIGJ,BAIJQ,TANGCH,etal.Characteristicsoflaminarseparationflutteroftwo-dimensionalairfoilsatlowReynoldsnumbersJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121280. (责任编辑:李明敏)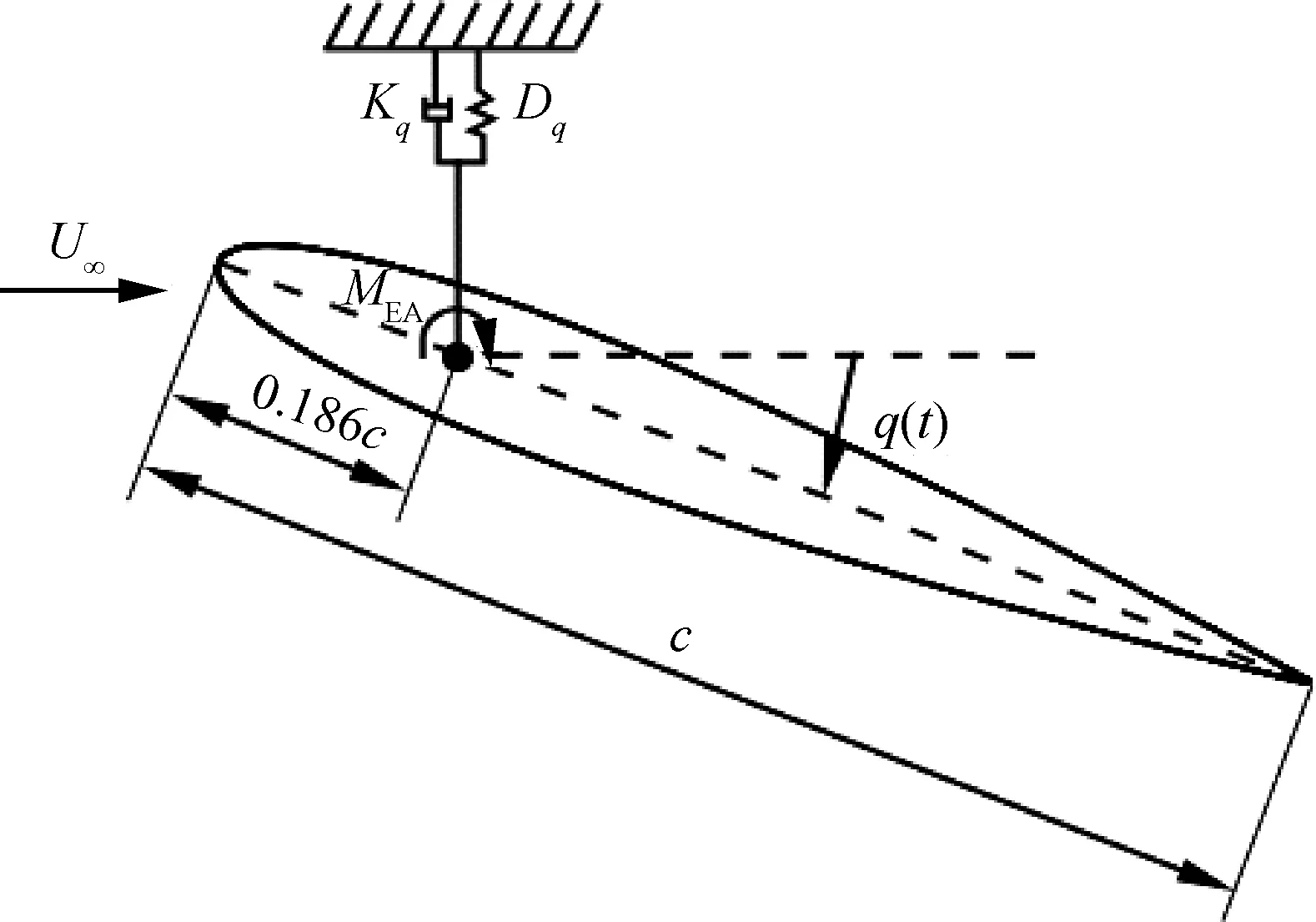
4.2 数值模拟精度验证
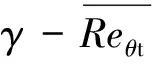
4.3 层流分离颤振特性分析

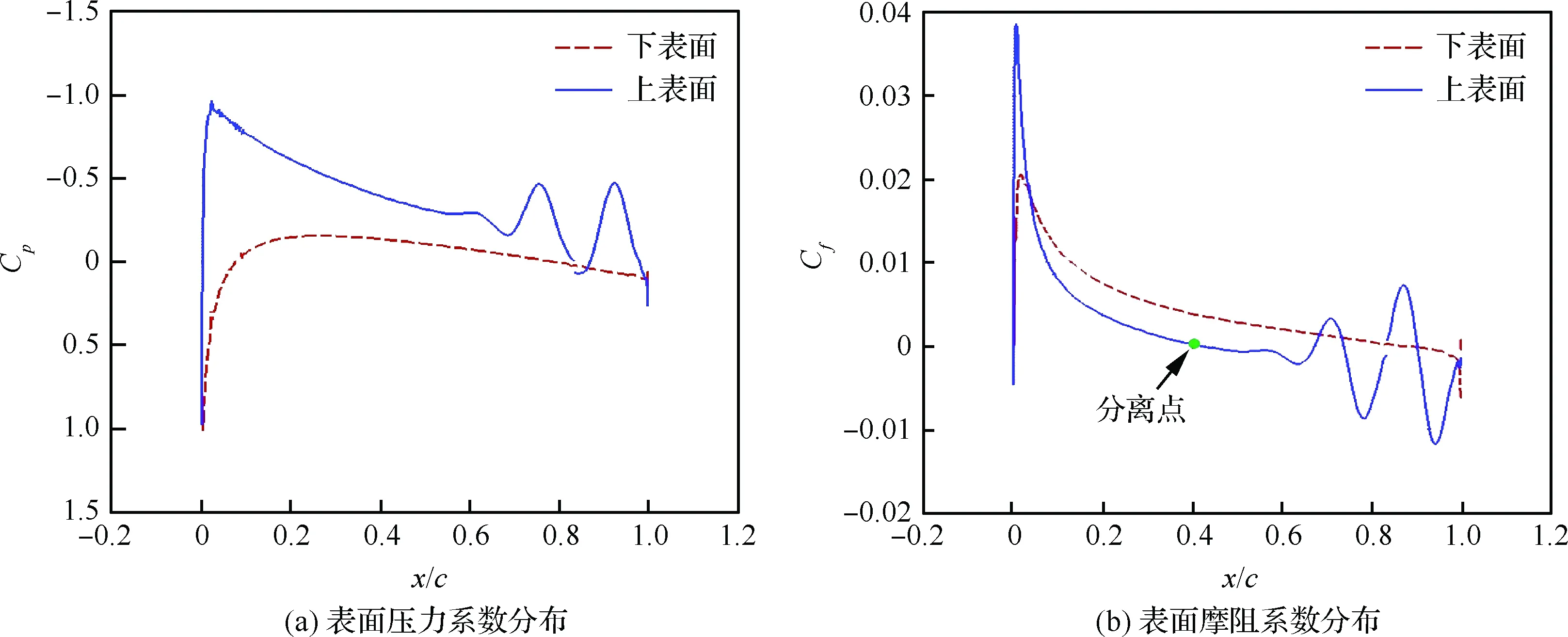
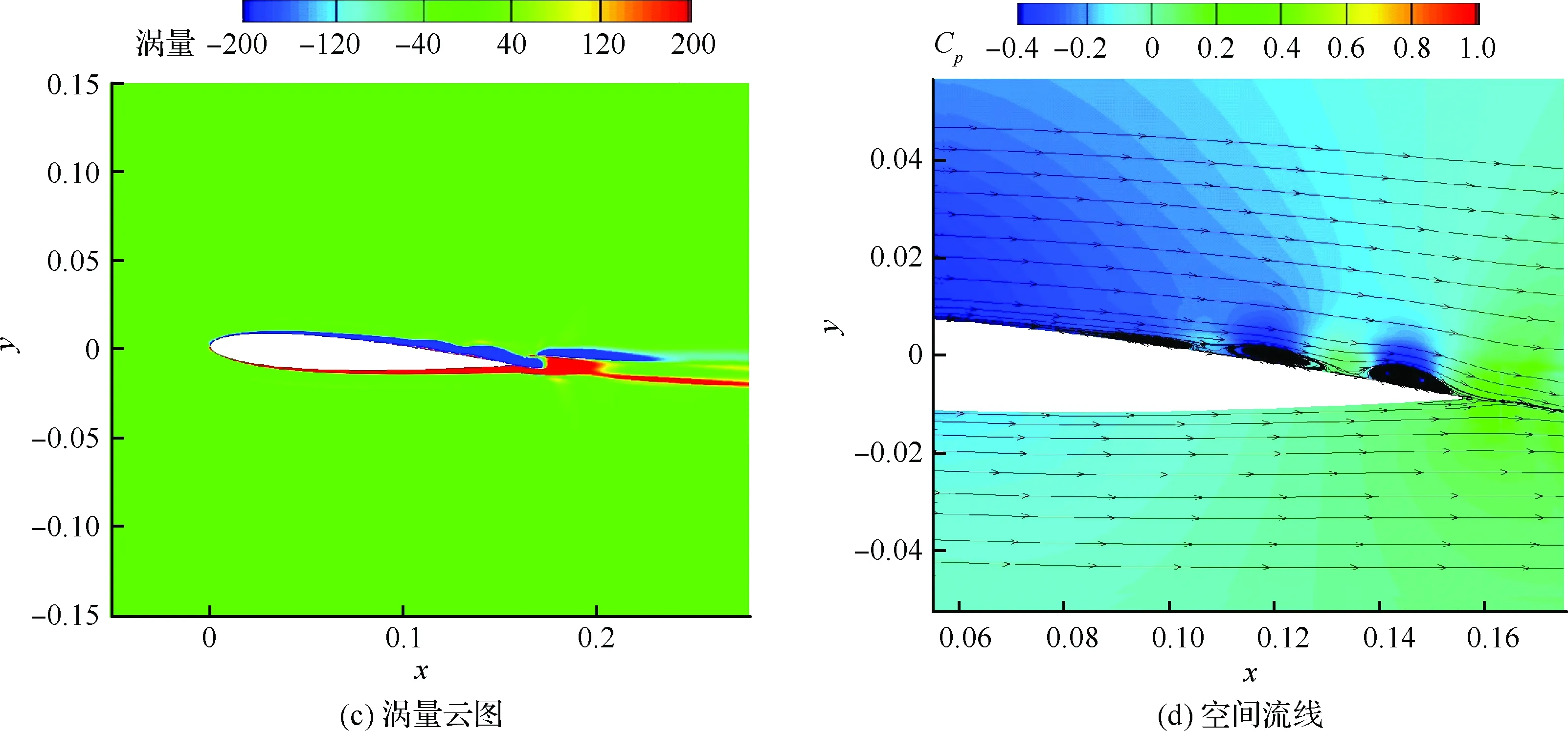
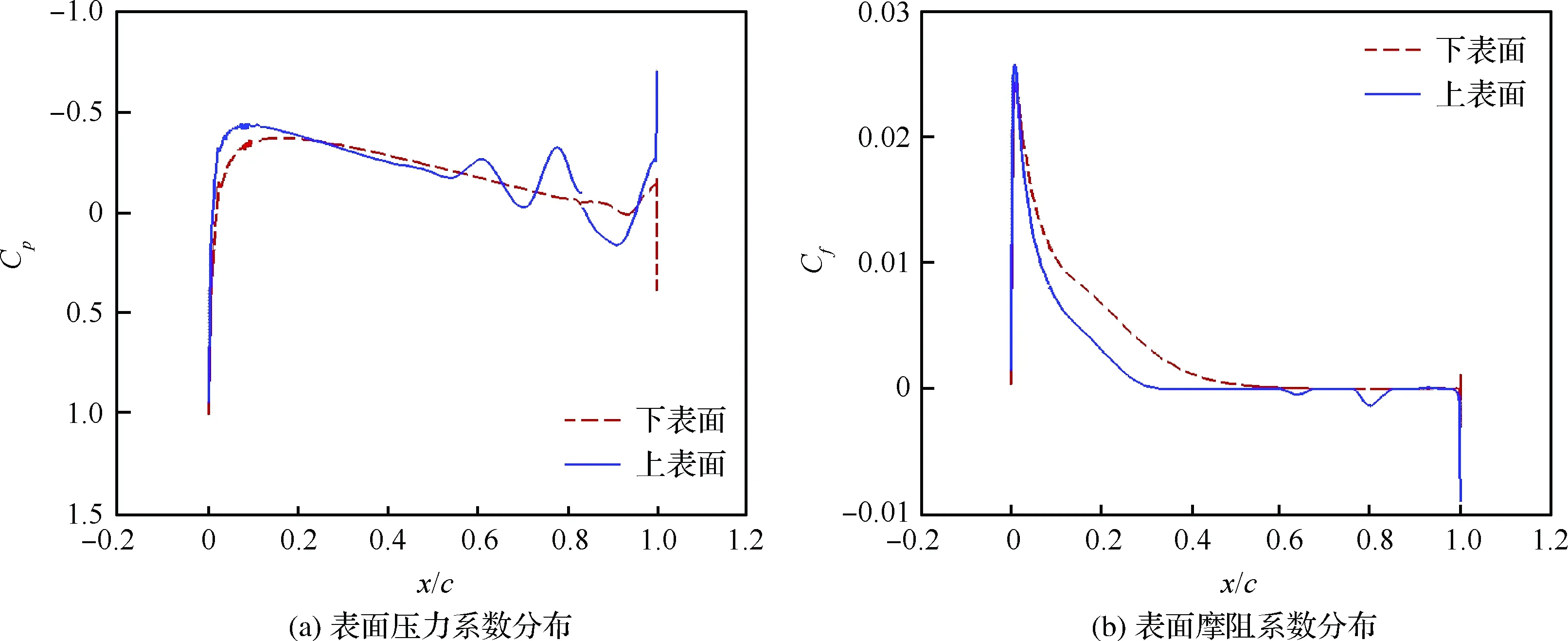
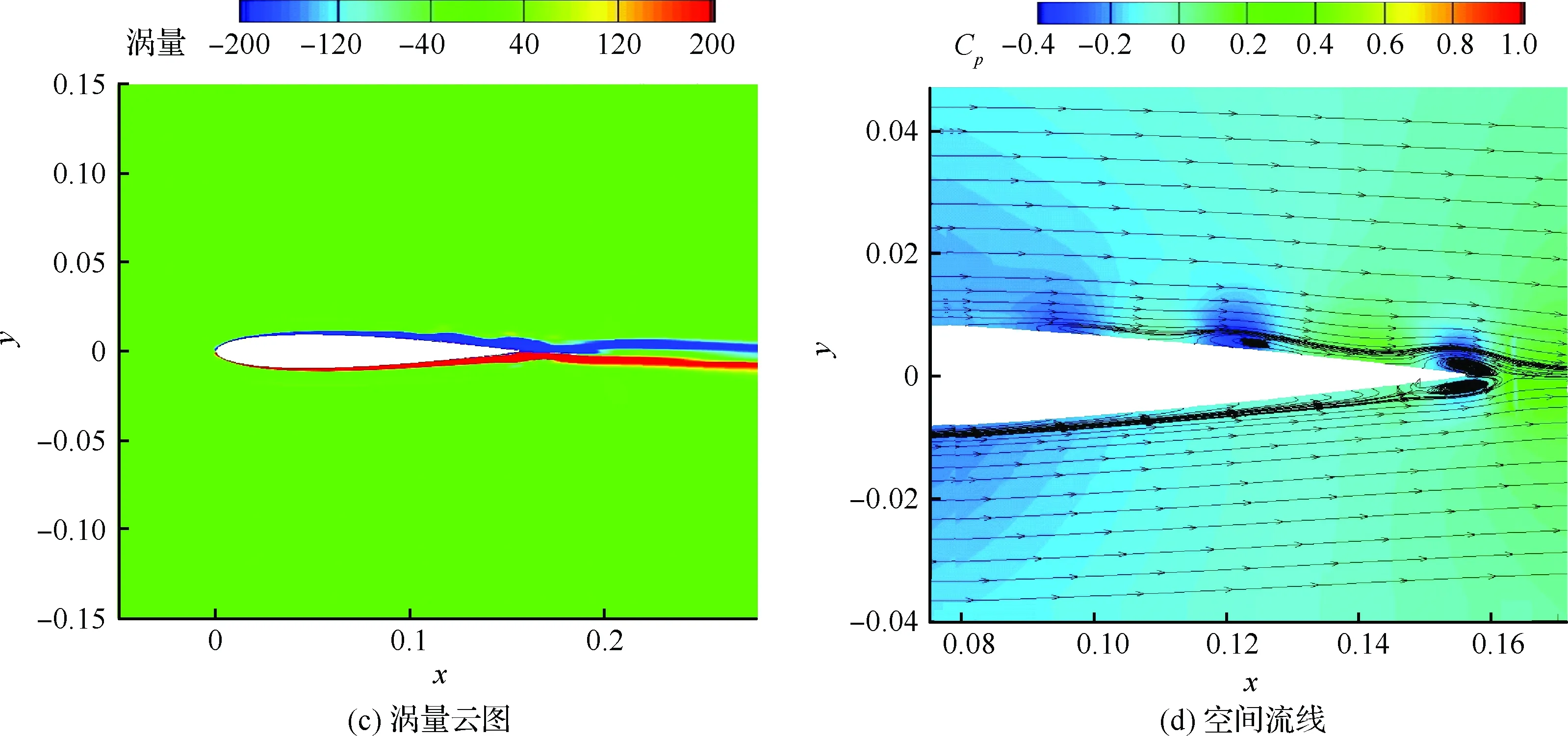
5 不同因素对层流分离颤振的影响
5.1 来流湍流度

5.2 翼型厚度
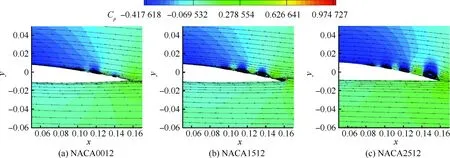
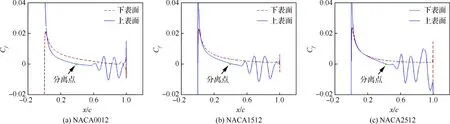
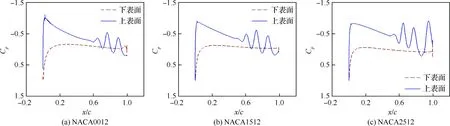
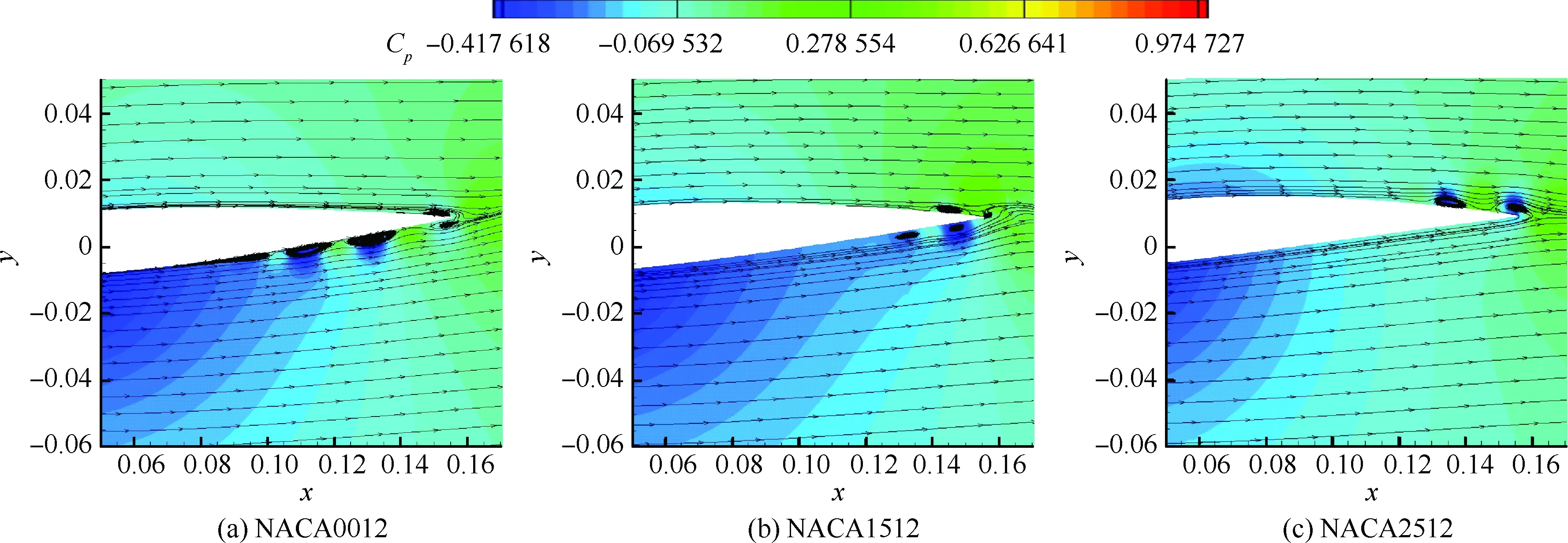
5.3 翼型弯度

6 结 论