可压缩流湍流度变热线过热比测量方法
杜钰锋,林俊,马护生,熊能
中国空气动力研究与发展中心,绵阳 621000
可压缩流湍流度变热线过热比测量方法
杜钰锋,林俊*,马护生,熊能
中国空气动力研究与发展中心,绵阳 621000
开展了可压缩流中湍流度测量技术的研究,以满足高速风洞高精度试验能力的需求。以对流换热规律为基础,从理论上对可压缩流中热线金属丝热平衡关系式进行了推导,以此为基础,详细推导了恒温热线风速仪的响应关系式,得到了质量流量和总温灵敏度系数的显式表达式,建立了可压缩流中湍流度的求解方法。在马赫数为0.3~0.6范围内进行了湍流度测量试验,以响应关系式为数学模型,利用双曲线拟合方法对试验数据进行了拟合分析,求解得到了马赫数在0.3~0.6范围内流场湍流度约为0.3%~0.6%。对热线输出电压进行了频谱分析,根据频谱特性,利用低通滤波对频域信号进行了处理,有效降低了时域信号脉冲尖峰对湍流度求解的影响,滤波后求解得到马赫数在0.3~0.6范围内流场湍流度约为0.1%~0.3%,与前期测量结果相符。试验结果证明了所建立理论方法的正确性及利用恒温热线风速仪变过热比方法测量可压缩流湍流度的可行性。
可压缩流;湍流度;恒温热线风速仪;过热比;响应关系式;双曲线拟合;低通滤波
风洞试验是对飞行器进行空气动力学研究最为有效的手段,是飞行器研制与开发过程中进行复杂气动特性研究不可或缺的环节[1]。随着飞行器性能的不断提升,对风洞试验的准确性要求越来越高,而优异的风洞流场品质是生产高质量数据的前提。
风洞流场湍流度作为一项重要的动态流场品质,一直以来并没有得到充分的重视,但随着对风洞扰动机理的深入探索,国外学者率先深刻认识到湍流度的重要性并开始注重对其的测量与研究。Dryden与Kuethe首次应用热线风速仪对低速风洞流场速度脉动进行测量,并改善了当时热线风速仪存在的响应频率过低的问题[2]。该团队应用热线风速仪对低速风洞中湍流尺度进行了测量,以圆球为对象,研究了湍流尺度对风洞试验模型阻力测量的影响,提出了与湍流度、湍流尺度、特征长度相关的无量纲参数[3-4]。从上述文献可总结出:第一,热线风速仪由于其分辨率高、响应频率高等优点,在风洞湍流度测量试验中得到了广泛的应用;第二,由于热线风速仪对于低速不可压缩流动的响应关系式较为明确[5],因此在湍流度测量技术研究的初期,低速风洞流场湍流度测量的难关率先被攻克,并逐渐形成了系统化、标准化的测量方法与流程[6]。然而,热线风速仪在可压缩流动中输出电压受到气体速度、密度、总温的耦合作用,其响应关系式并不明确[7],因此,以热线风速仪为基础的高速风洞流场湍流度测量技术的难度远高于低速风洞,且发展时间也晚于低速风洞。Horstman与Rose根据大量跨声速风洞湍流度测量试验数据,研究了热线风速仪对气体速度、密度、总温灵敏度系数的求解方法,得到了灵敏度系数与表征对流换热强度的努赛尔数Nu、雷诺数Re、马赫数Ma等无量纲系数之间的微分函数关系,并在此基础上求出了跨声速风洞流场湍流度。然而,该方法在求解过程中可能遇到方程系数矩阵条件数过高,导致矩阵近似奇异而难以求逆矩阵的问题,此时将无法准确求出湍流度[8]。Stainback与Johnson对亚声速风洞中可压缩流的湍流度测量进行了初步研究,通过热线风速仪校准试验,利用控制变量法分别求出了速度、密度、总温灵敏度系数,进而求解出湍流度。但该方法需要大量试验数据来对热线风速仪的灵敏度系数进行校准,对热线探针的使用寿命十分不利,且同样可能会遇到求解方程过程中系数矩阵近似奇异难以求逆矩阵的问题[9]。
与以上两篇文献类似,还有一些研究人员致力于通过校准试验对可压缩流中热线风速仪的灵敏度系数进行求解,进而求解湍流度,取得了一定的成果[10-13]。与以上方法稍有不同,Kovasznay利用热线风速仪对超声速风洞中流场湍流度进行了测量,由于超声速流中速度与密度灵敏度系数近似相等,因此作者利用大量试验数据,提出了质量流量与总温灵敏度系数的经验公式[14],利用脉动图对试验数据进行拟合,进而求解流场湍流度[15],该方法无需大量校准数据,极大提升了湍流度测量效率,但由于灵敏度系数为试验数据总结得到的经验公式,该方法缺乏一定的理论基础。
国内对于湍流度测量技术的研究起步较晚,自20世纪90年代开始,才逐渐有相关研究成果出现。何克敏与白存儒利用热线风速仪对翼型边界层中湍流度及雷诺应力进行了测量,并分析了湍流度对雷诺应力分布规律的影响[16]。王庶与米建春利用热膜探针对超低雷诺数下流场湍流度进行了测量,并研究了升力系数与阻力系数与湍流度的关系[17]。王晋军与兰世隆利用激光多普勒测速技术(LDV)对沟槽面边界层中湍流度分布进行了精细化测量,对沟槽面减阻作用进行了探索[18]。还有一些学者,如许宏庆和费维扬[19]、沈建平等[20],利用LDV对不同工况下流场湍流度进行了测量,取得了一定的成果。然而,由以上文献可以看出,国内湍流度测量技术研究大多集中在低速不可压缩流领域,且多为应用研究,可压缩流中的研究相对较少。
本文从理论上推导了可压缩流中恒温热线风速仪的响应关系式,利用双曲线对试验数据拟合,建立了湍流度的求解方法。在马赫数为0.3~0.6范围内进行了湍流度测量试验,利用低通滤波对热线输出电压信号进行了处理,求解得到流场湍流度,与前期试验结果相符,验证了所建立方法的可行性。
1 恒温热线风速仪响应关系式理论推导
1.1 热线金属丝热平衡关系式推导
热线探针作为热线风速仪的传感器,其敏感元件一般为直径5 μm、长度1.25 mm的钨、铂或其合金的金属丝,当其放置于流场当中时,热线金属丝与周围气体发生受迫对流传热,其传热关系式为[21]
Q=hA0ΔT
(1)
式中:Q为热线探针与气体单位时间对流传热量;h为对流传热系数;A0=πld为对流换热面积,l与d分别为热线金属丝的长度和直径;ΔT=Tw-Te为热线金属丝与气体的平均温度差,Tw为通电加热时热线金属丝的温度,Te为未通电加热时,热线金属丝受气体加热的温度,即为气体在热线金属丝表面滞止的平均温度,因此用Te代表此时气体温度更为合理。Te与气体总温T0很相近,且有
Te=ηT0
(2)
式中:η为温度恢复系数。在可压缩流中,η≈0.99[22]。
引入表示对流换热强度的无量纲数Nu,

(3)
式中:λ0为气体热导率。
综合式(1)~式(3)可得热线金属丝传热关系式为
Q=πlλ0(Tw-Te)Nu
(4)
根据King于1914年在文献[5]中的研究成果,热线风速仪在不可压缩流中的无量纲响应关系式(King公式)为
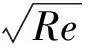
(5)
式中:A、B为校准系数。式(5)很好地描述了热线风速仪在不可压缩流中的无量纲响应关系式,至今仍被广泛使用。然而,在可压缩流中,式(5)不再适用。Kovasznay于1950年在文献[14]中,根据大量校准试验数据对式(5)进行了改进,提出了适用于可压缩流的无量纲响应关系式:
(6)
式中:C为校准系数。由于求解校准系数A、B与C需要大量校准试验数据,且式(6)中变量较多,Tw等温度变量不直观,难以直接测得,因此校准系数求解难度较大。考虑引入热线风速仪过热比,即
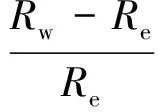
(7)
式中:Rw为热线金属丝在温度Tw时的电阻值;Re为热线金属丝在温度Te时的电阻值。根据电阻与温度的计算公式可得
Rw=R*[1+α*(Tw-T*)]
(8)
Re=R*[1+α*(Te-T*)]
(9)
式中:T*为参考温度;R*为热线金属丝在参考温度时的电阻值;α*为参考温度时的电阻温度系数。式(8)减去式(9)可得
Rw-Re=α*R*(Tw-Te)
(10)
整理式(7)、式(10)可得

(11)
将式(11)代入式(6)可得
(12)
风洞试验来流条件固定时,C、Re、α*、R*与T0均为常数,因此可用标准系数k对式(12)中的常数项进行替换,即
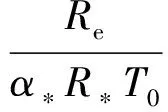
(13)
将式(13)代入式(12)中可得热线风速仪在可压缩流中的无量纲响应关系式为
(14)
将式(14)代入式(4)可得热线金属丝传热关系式为
(15)
由恒温热线风速仪原理可知,为保持热线金属丝温度不变,其电产热量应与对流换热量保持相等[23],可得热线金属丝热平衡关系式为
(16)
式中:E为热线金属丝两端电压;I为通过热线金属丝的电流。
1.2 恒温热线风速仪响应关系式推导
流场湍流度Tu定义为
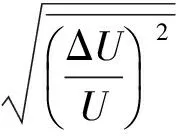
(17)
式中:U为气体速度;ΔU为气体瞬时速度与速度均值的差值,即为速度脉动。由式(17)可知,若想求得湍流度,需求得速度脉动与速度均值的比值。因此,对式(16)进行先取自然对数,再求偏导数的处理(后文简称∂ln处理),可得
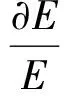
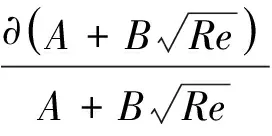
(18)
对式(18)各项逐项处理,以期得到仅包含电路和流场基本量的形式,进而求解湍流度。
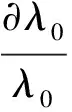
由于空气的热导率以及动力黏度随总温的升高而升高,且通过对实测数据分析,存在以下关系式[24]:
(19)
式中:μ0为空气的动力黏度;下标*表示在参考温度下变量的值。对式(19)进行∂ln处理,可得
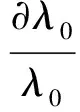
(20)
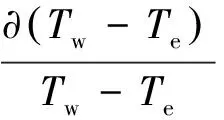
对式(8)进行∂ln处理,可得

(21)
整理式(21)以获得∂Tw,可得
(22)
对式(2)进行求偏导数的处理,可得
∂Te=η∂T0
(23)
由式(11)可得
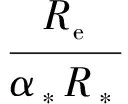
(2)驱动参数。胶带与滚筒的摩擦系数取0.3,Ⅰ号驱动滚筒直径为Φ1 450 mm,围包角167°;Ⅱ号驱动滚筒直径为Φ1 450 mm,围包角184°;改向滚筒直径为Φ1 000 mm;电动机功率800 kW,电压10 kV,共3台;功率配比Ⅰ∶Ⅱ=2∶1;CST型号:CST1120kV,i=25.0345,共3台。
(24)
整理式(7)、式(22)~式(24)可得

(25)
导体的电阻R符合电阻公式

(26)
式中:ρ0为导体的电阻率;L为导线长度;S为导线横截面积。对于参考温度下的热线金属丝,电阻率为常数,式(26)可退化为
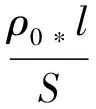
(27)
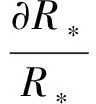
(28)
对圆形面积公式S=πd2/4进行∂ln处理,可得
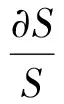
(29)
引入热线金属丝的泊松比μ,
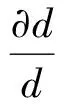
(30)
整理式(28)~式(30),可得
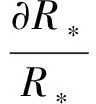
(31)
将式(31)代入式(25),可得

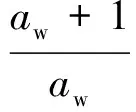
(32)
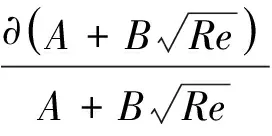
雷诺数Re定义为
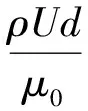
(33)
式中:ρ为气体密度。
对式(33)进行∂ln处理,可得

(34)
整理式(20)、式(30)和式(34)可得

(35)
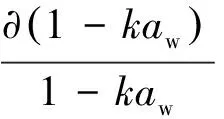
对式(7)进行∂ln处理,可得
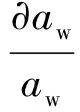
(36)
整理式(7)和式(36),可得
(37)
对式(9)进行∂ln处理,可得
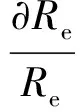
(38)
整理式(9)、式(23)、式(31)和式(38),可得
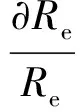
(39)
整理式(37)和式(39),可得
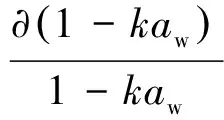
(40)
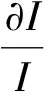
热线金属丝两端电压与通过的电流符合欧姆定律:
E=IRw
(41)
对式(41)进行∂ln处理,可得
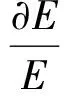
(42)
与式(31)类似,

(43)
将式(20)、式(32)、式(35)、式(40)、式(42)和式(43)代入式(18),并用Δ代替∂(均为小量),整理可得
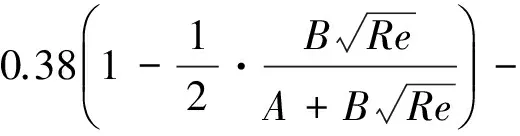
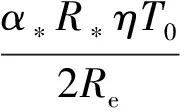
(44)
由于热线探针在制造过程中,热线金属丝留有一定的松弛度,且整个测量系统需保证一定的刚度要求,因此在湍流度测量试验中,可忽略热线金属丝的应变效应[25],式(44)可退化为
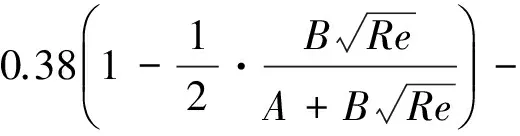
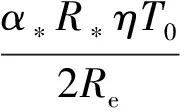
(45)
式(45)即为恒温热线风速仪响应关系式。
1.3 校准系数k求解方法推导
式(45)中,除了根据流场及电路条件确定的已知量及待求量外,还有校准系数A、B和k未知。其中,A、B为根据式(5)对热线风速仪进行不可压缩流校准获得的系数,k的求解方法为
将式(7)、式(11)和式(41)代入式(16),可得
(46)
2 数据分析方法
2.1 双曲线拟合方法的建立
在获得恒温热线风速仪响应关系式后,需考虑如何对变过热比湍流度测量试验数据进行处理。参考文献[15],利用式(45)恒温热线风速仪响应关系式,建立适用于高速风洞可压缩流中的双曲线拟合方法。
对式(45)进行变形:

(47)
式(47)中各变量含义为
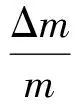
(48)
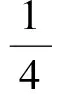
(49)
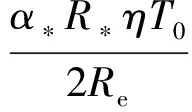
0.38(1-2FCTA)
(50)
式中:m为气体质量流量;FCTA为恒温热线风速仪质量流量灵敏度系数;GCTA为恒温热线风速仪总温灵敏度系数。
式(47)左右同时除以GCTA,可得
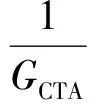
(51)

(52)
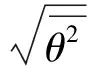

(53)
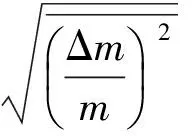
(54)
2.2 湍流度求解方法的建立
由式(48)可知,若想求出湍流度,需从质量流量脉动中将速度脉动分离出来。
考虑一维等熵流的能量方程:

(55)
式中:cp为气体定压比热容;T为气体静温。
完全气体状态方程:
p=ρRT
(56)
式中:p为气体静压;R为气体常数。
定压比热容与气体常数有如下关系:

(57)
式中:γ为气体比热比。
将式(56)和式(57)代入式(55)可得

(58)
对式(58)进行求偏导数的处理,可得

(59)
声速及马赫数定义为
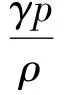
(60)

(61)
式中:c为声速。
将式(55)、式(60)和式(61)代入式(59),并用Δ代替∂(均为小量),整理可得
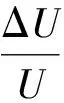
(62)
根据文献中利用LDV进行可压缩流湍流度测量试验数据,在可压缩流中,压力脉动相比其余项可忽略[26],因此式(62)可退化为
(63)
联立式(48)和式(63),可以解得湍流度
(64)
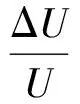
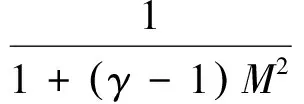
(65)
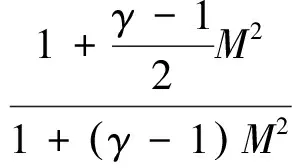
(66)
3 湍流度测量试验
3.1 探针校准风洞
为发展内流测试技术,建设了探针校准风洞,以期实现总压探针、五孔探针等气动探针的校准。为评估探针校准精度,对探针校准风洞开展了湍流度测量试验。该风洞采用直吹射流式布局,其主要技术参数为:马赫数调节范围为0.05~1.0,总压调节范围为0.05~0.25 MPa,总温调节范围为278~330 K,其结构示意图如图1所示。
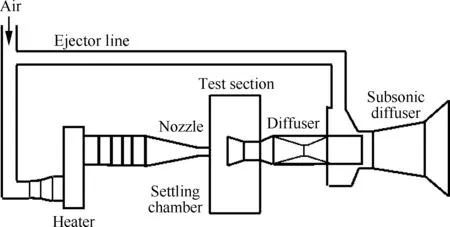
图1 探针校准风洞示意图Fig.1 Schematic of probe calibration wind tunnel
3.2 恒温热线风速仪
本次湍流度测量试验使用的是IFA300型恒温热线风速仪及一支TSI单丝热线探针。恒温热线风速仪原理为:将热线电阻接入惠斯通电桥的一臂,利用电桥与运算放大器组成反馈系统,以保证热线电阻温度(电阻值)不变,通过记录热线风速仪输出电压信号来对流场信息进行分析。所使用的TSI热线探针材料为铂,其尺寸参数为:d=50.8 μm,l=1.02 mm;其电阻参数为:参考温度T*=273 K 时,α*=0.002 4/K,R*=5.65 Ω,Re=5.84 Ω。
3.3 湍流度测量试验结果
在前文所述的探针校准风洞中进行湍流度测量试验。为避免热线金属丝被高速气流中携带的微小颗粒撞断,目前仅在马赫数范围Ma=0.3~0.6的可压缩流中进行试验,过热比设定范围为0.04~0.30。
利用式(46)对不同试验状态下校准系数k进行拟合求解,k及拟合优度G2结果如表1所示。

表1 校准系数k求解结果Table 1 Calculation results of calibration coefficient k

以式(52)为数学模型,对表2~表5中的计算结果进行双曲线拟合,结果如图2所示。
图2(a)~图2(d)中,散点为表2中的数据点,虚线为其渐近线,实线为对数据点进行拟合的双曲线,拟合优度结果如表6所示。根据式(54),对图中渐近线斜率进行计算,可得质量流量脉动与其均值比值的均方根值,利用式(64)~式(66)可计算得到湍流度Tu,结果如表6所示。
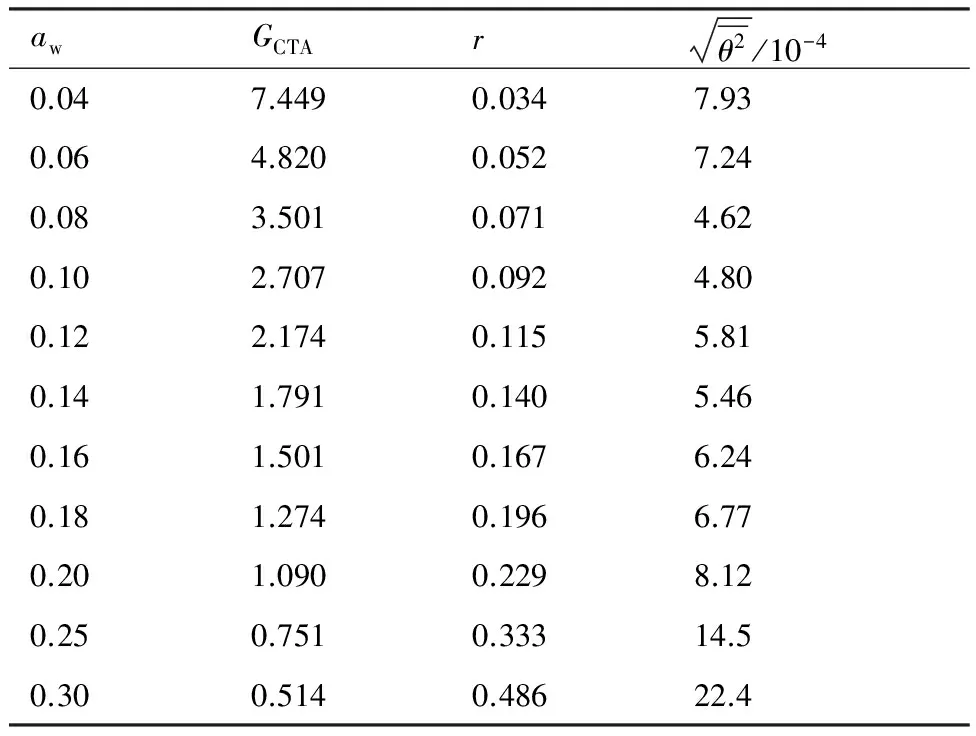
表2 式(45)中参数求解结果(Ma=0.330,T0=276.5 K)
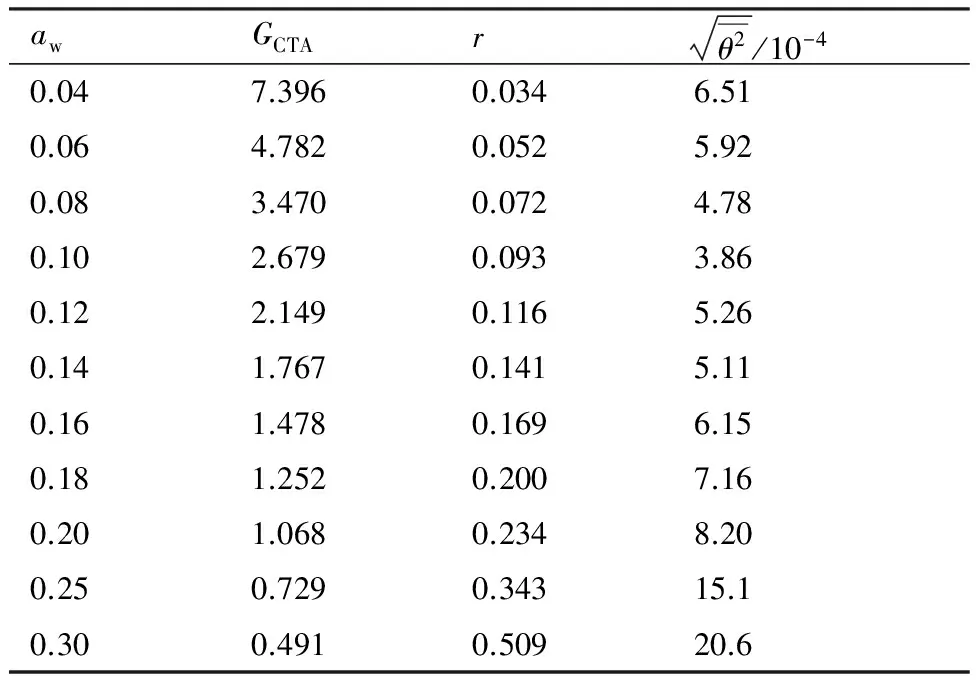
表3 式(45)中参数求解结果(Ma=0.420,T0=275 K)

表4 式(45)中参数求解结果(Ma=0.525,T0=277.5 K)

表5 式(45)中参数求解结果(Ma=0.627,T0=278 K)

图2 双曲线拟合结果Fig.2 Results of hyperbola fitting
表6 湍流度计算结果Table 6 Calculation results of turbulence level

MaG2Δmm()2%Tu/%0.3300.9957 0.590.640.4200.9816 0.470.470.5250.9748 0.360.350.6270.9804 0.320.32
由表6中拟合优度数据可知,双曲线拟合方法对试验数据拟合效果较好。由于总温脉动与其均值比值的均方根值远小于质量流量脉动与其均值比值的均方根值,且式(64)中H、J量值相当,因此求得的湍流度与质量流量脉动与其均值比值的均方根值量值相近,且与预期量级相符。
在Ma=0.3~0.6范围内,湍流度随马赫数提高而降低,根据国外高速风洞流场品质数据显示,在亚声速范围内,湍流度随马赫数变化并无明显规律可循,而是与风洞结构、流场条件、运行方式等诸多因素有关[27-29]。
对热线输出电压进行傅里叶变换,以分析其频谱特性,由于热线测试系统已经预设高频空间电磁辐射、市电工频抗干扰措施(如仪器金属外壳、屏蔽线等电磁屏蔽装置),因此可忽略高频空间电磁辐射、市电工频对热线输出电压的影响。对频域进行滤波处理,而后再对湍流度进行求解。由于输出电压数据组数过多(4个马赫数状态,每个马赫数下11个过热比,共44组数据),因此文中仅选其二为代表进行说明。
由热线风速仪记录的输出电压脉动E随时间t的变化如图3所示。

图3 热线输出电压脉动Fig.3 Hot-wire output voltage fluctuation
图4 傅里叶变换后的单边幅频谱Fig.4 Single-sided amplitude spectrum after Fourier transform
傅里叶变换后单边幅频谱图如图4所示,图中纵轴|Y(f)|为信号经傅里叶变换后的幅频强度,f为频率。由图4可以看出,热线输出电压信号能量主要集中在10 kHz以下的频段内,10 kHz以上的高频信号即对应图3中的输出电压脉冲尖峰。以10 kHz为阈值,采用低通滤波对输出电压脉动信号进行滤波,并通过傅里叶逆变换将滤波后的频域信号转换为时域信号,结果如图5所示。
对比图3、图5可知,经过低通滤波后,热线输出电压信号均值不变,脉冲尖峰明显减弱,滤波效果较好。
重复进行上述湍流度求解过程,对滤波后的热线输出电压信号进行湍流度求解(由于内容重复,不再赘述),可求得各马赫数下湍流度如表7所示。
图5 滤波后电压脉动Fig.5 Voltage fluctuation after filtering
表7 滤波后湍流度计算结果
Table 7 Calculation results of turbulence levelafter filtering
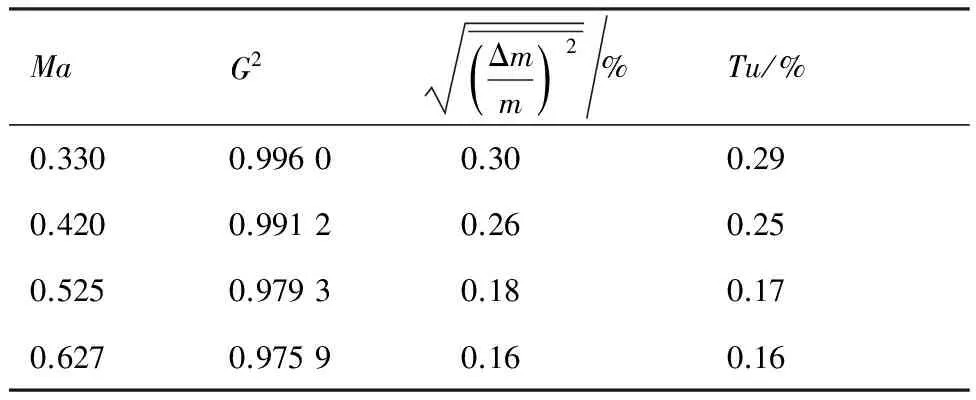
MaG2Δmm()2%Tu/%0.3300.9960 0.300.290.4200.9912 0.260.250.5250.9793 0.180.170.6270.9759 0.160.16
由表7中拟合优度数据可知,双曲线拟合方法对滤波后试验数据拟合效果较好。对比表6、表7中数据,可作滤波前后湍流度对比图,如图6所示。
由图6可知:在滤除热线输出电压脉冲尖峰后,湍流度测量值明显降低,说明脉冲尖峰对湍流度计算影响较大。在Ma=0.3~0.6时,湍流度水平为0.1%~0.3%左右,与前期热线校准试验湍流度测量值相符[13],验证了所建立的可压缩流中热线响应关系式及双曲线拟合方法的有效性及应用恒温热线风速仪测量可压缩流湍流度的可行性。

图6 滤波前后湍流度对比Fig.6 Contrast of turbulence level before and after filtering
4 结 论
1) 推导了恒温热线风速仪在可压缩流中的响应关系式,以该关系式为数学模型,建立了变热线风速仪过热比湍流度测量试验数据的双曲线拟合方法。
2) 在Ma=0.3~0.6范围内进行了可压缩流湍流度测量试验,利用所建立的方法对流场湍流度进行了求解,对热线输出电压进行了频谱分析,利用低通滤波对输出电压中存在的脉冲尖峰进行了处理,进而求解出滤波处理后的流场湍流度,其量值合理,与前期测量结果相符,验证了所建立的方法的有效性。
3) 变热线过热比测量湍流度的方法无需对热线风速仪进行校准,极大地缩短了试验中热线探针的工作时间,对寿命有限的探针起到了有效的保护,且提高了湍流度测量试验的效率。
[1] ZAKS H A. 实验空气动力学原理[M]. 詹承禹, 译. 北京: 国防工业出版社, 1956: 42-44.
ZAKS H A. Experimental aerodynamics[M]. ZHAN C Y, translated. Beijing: National Defense Industry Press, 1956: 42-44 (in Chinese).
[2] DRYDEN H L, KUETHE A M. The measurement of fluctuations of air speed by the hot-wire anemometer: NACA-REPORT-320[R]. Washington,D. C.: NACA, 1930.
[3] DRYDEN H L, KUETHE A M. Effect of turbulence in wind tunnel measurements: NACA-REPORT-342[R]. Washington, D. C.: NACA, 1931.
[4] DRYDEN H L, SCHUBAUER G B, MOCK W C, et al. Measurements of intensity and scale of wind-tunnel turbulence and their relation to the critical Reynolds number of spheres: NACA-REPORT-581[R]. Washington, D. C.: NACA, 1937.
[5] KING L V. On the convection of heat from small cylinders in a stream of fluid: Determination of the convection constants of small platinum wires with application to hot-wire anemometry[J]. Philosophical Transactions of the Royal Society A—Mathematical Physical and Engineering Science, 1914, 214: 373-432.
[6] RESHOTKO E, SARIC W S, NAGIB H M. Flow quality issues for large wind tunnel: AIAA-1997-0225[R]. Reston, VA: AIAA, 1997.
[7] BRUUN H H. Hot-wire anemometry: Principles and signal analysis[M]. New York: Oxford University Press, 1995: 304-316.
[8] HORSTMAN C C, ROSE W C. Hot-wire anemometry in transonic flow: NASA-TM-X-62495[R]. Washington, D.C.: NASA, 1976.
[9] STAINBACK P C, JOHNSON C B. Preliminary measurements of velocity, density and total temperature fluctuations in compressible subsonic flow: AIAA-1983-0384[R]. Reston, VA: AIAA, 1983.
[10] JONES G S, STAINBACK P C, HARRIES C D, et al. Flow quality measurements for the Langley 8-foot transonic pressure tunnel LFC experiment: AIAA-1989-0150 [R]. Reston, VA: AIAA, 1989.
[11] JONES G S, STAINBACK P C, NAGABUSHANA K A. A comparison of calibration techniques for hot-wires operated in subsonic compressible slip flows: AIAA-1992-4007[R]. Reston, VA: AIAA, 1992.
[12] NAGABUSHANA K A, STAINBACK P C, JONES G S. A rational technique for calibrating hot-wire probes in subsonic to supersonic speeds: AIAA-1994-2536[R]. Reston, VA: AIAA, 1994.
[13] 杜钰锋, 林俊, 马护生, 等. 可压缩流体恒温热线风速仪校准方法[J]. 航空学报, 2017, 38(6): 120600.
DU Y F, LIN J, MA H S, et al. Calibration method for constant temperature hot-wire anemometer for compressible fluid[J]. Acta Aeronautics et Astronautics Sinica, 2017, 38(6): 120600 (in Chinese).
[14] KOVASZNAY L S G. The hot-wire anemometer in supersonic flow[J]. Journal of the Aeronautical Sciences, 1950, 17(9): 565-572.
[15] KOVASZNAY L S G. Turbulence in supersonic flow[J]. Journal of the Aeronautical Sciences, 1953, 20(10): 657-682.
[16] 何克敏, 白存儒. 极低湍流度下翼型近场尾流雷诺切应力的分布[J]. 应用力学学报, 1997, 14(2): 19-26.
HE K M, BAI C R. The Reynolds shear stress distribution in the near wake of an airfoil at very low turbulence level[J]. Chinese Journal of Applied Mechanics, 1997, 14(2): 19-26 (in Chinese).
[17] 王庶, 米建春. 大湍流度对超低雷诺数下翼型受力及绕流的影响[J]. 航空学报, 2011, 32(1): 41-48.
WANG S, MI J C. Effect of large turbulence intensity on airfoil load and flow[J]. Acta Aeronautics et Astronautics Sinica, 2011, 32(1): 41-48 (in Chinese).
[18] 王晋军, 兰世隆. 沟槽面湍流边界层湍流度分布[J]. 北京航空航天大学学报, 1998, 24(2): 178-180.
WANG J J, LAN S L. Turbulence intensities distributions over a riblets surface[J]. Journal of Beijing University of Aeronautics and Astronautics, 1998, 24(2): 178-180 (in Chinese).
[19] 许宏庆, 费维扬. 用LDV系统测量转盘萃取塔内流场[J]. 实验力学, 1995, 10(4): 316-322.
XU H Q, FEI W Y. The measurement of flow field in a rotating disc contactor with LDV[J]. Journal of Experimental Mechanics, 1995, 10(4): 316-322 (in Chinese).
[20] 沈建平, 吴承雄, 朱隆碧, 等. 用LDV研究柴油机不同燃烧室对缸内湍流场的影响[J]. 内燃机学报, 1995, 13(1): 19-27.
SHEN J P, WU C X, ZHU L B, et al. Investigation on effects of different piston-bowl structures on in-cylinder turbulent flow field of diesel engine by LDV[J]. Transactions of CSICE, 1995, 13(1): 19-27 (in Chinese).
[21] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006: 197-202.
YANG S M, TAO W Q. Heat transfer[M]. Beijing: Higher Education Press, 2006: 197-202 (in Chinese).
[22] BALDWIN L V, SANDBORN V A, LAURENCE J C. Heat transfer from transverse and yawed cylinders in continuum, slip, and free molecule air flows[J]. Journal of Heat Transfer, 1960, 82(2): 77-86.
[23] JANSSEN J M L, ENSING L, VAN ERP J B. A constant-temperature-operation hot-wire anemometer[J]. Proceedings of the IRE, 1959, 46(4): 555-567.
[24] INCROPERA F P, DEWITT D P, BERGMAN T L, 等. 传热和传质基本原理[M]. 葛新石, 叶宏, 译. 北京: 化学工业出版社, 2009: 36-41, 572.
INCROPERA F P, DEWITT D P, BERGMAN T L, et al. Fundamentals of heat and mass transfer[M]. GE X S, YE H, translated. Beijing: Chemical Industry Press, 2009: 36-41, 572 (in Chinese).
[25] 盛森芝. 热线热膜流速计[M]. 北京: 中国科学技术出版社, 2003: 17-22.
SHENG S Z. Hot wire/film anemometer[M]. Beijing: Science and Technology of China Press, 2003: 17-22 (in Chinese).
[26] ROSE W C, MCDAID E P. Turbulence measurement in transonic flow[J]. AIAA Journal, 1977, 15(9): 1368-1370.
[27] BOBBITT C, EVERHART J, FOSTER J, et al. National transonic facility characterization status: AIAA-2000-0293[R]. Reston, VA: AIAA, 2000.
[28] AMAYA M A, MURTHY S V. Flow quality measurements in the NASA Ames upgraded 11-by 11-foot transonic wind tunnel: AIAA-2000-2681[R]. Reston, VA: AIAA, 2000.
[29] KRYNYTZKY A J, HERGERT D W. Boeing transonic wind tunnel upgrade assessment: AIAA-2002-2782[R]. Reston, VA: AIAA, 2002.
Measurementtechniqueforturbulencelevelincompressiblefluidbychangingoverheatratioofhot-wire
DUYufeng,LINJun*,MAHusheng,XIONGNeng
ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China
Turbulencelevelisimportantinhighspeedwindtunnelexperiments.Researchonmeasurementtechniquesforturbulencelevelincompressiblefluidiscarriedouttosatisfytheneedoftestswithhighaccuracyinhighspeedwindtunnel.Basedonthelawofheatconvection,responsefunctionofconstanttemperaturehot-wireanemometerisderivedindetail.Sensitivitiesofmassfluxandtotaltemperatureareobtained,andthealgorithmfortheturbulencelevelincompressiblefluidisbuilt.TurbulencelevelmeasurementtestsarecarriedoutwithMachnumbervaryingfrom0.3to0.6.Usingtheresponsefunctionproposedaboveasamathematicalmodel,thedataarefittedbasedonthehyperbolafittingmethod.Theturbulencelevelisaround0.3%-0.6%whentheMachnumbervariesfrom0.3to0.6.Thefrequencyspectrumofthehot-wireoutputvoltageisanalyzed.Accordingtothecharacteristicsofthefrequencyspectrum,thesignalisprocessedusinglow-passfiltering,andtheeffectofvoltagespikeinthetimedomainonthesolutionforturbulencelevelisreducedeffectively.Theturbulencelevelisaround0.1%-0.3%afterfilteringwithMachnumberrangingfrom0.3to0.6,andtheresultsarealmostthesamewithresultsobtainedpreviously.Theresultsvalidatecorrectnessofthesolutionforturbulencelevelandfeasibilityofapplicationofthetechniqueofchangingtheoverheatratiooftheconstanttemperaturehot-wireanemometerforturbulencelevelincompressiblefluid.
compressiblefluid;turbulencelevel;constanttemperaturehot-wireanemometer;overheatratio;responsefunction;hyperbolafitting;lowpassfiltering
2017-03-13;Revised2017-05-02;Accepted2017-06-11;Publishedonline2017-06-131318
URL:http://hkxb.buaa.edu.cn/CN/html/20171106.html
.E-mail1415776643@qq.com
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2017.121236
V211.71
A
1000-6893(2017)11-121236-12
2017-03-13;退修日期2017-05-02;录用日期2017-06-11;< class="emphasis_bold">网络出版时间
时间:2017-06-131318
http://hkxb.buaa.edu.cn/CN/html/20171106.html
.E-mail1415776643@qq.com
杜钰锋,林俊,马护生,等.可压缩流湍流度变热线过热比测量方法J. 航空学报,2017,38(11):121236.DUYF,LINJ,MAHS,etal.Measurementtechniqueforturbulencelevelincompressiblefluidbychangingoverheatratioofhot-wireanemometerJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121236.
(责任编辑:鲍亚平,蔡斐)
———重庆建成世界一流汽车风洞

