区间值决策表的决策风险最小化属性约简

徐菲菲

(上海电力学院 计算机科学与技术学院, 上海 200090)

区间值决策表的决策风险最小化属性约简

徐菲菲

(上海电力学院 计算机科学与技术学院, 上海 200090)

针对目前海量数据分析较多情况下从传统的单条记录转变为一个区间对象,将决策粗糙集中风险的概念引入至区间值决策表中,给出了区间值决策表决策风险的定义,并提出了决策风险最小化的属性约简方法.该方法可以保证所得到的约简集合相对于决策属性具有较强的分类能力,同时保证约简集合的决策风险最小.区间值决策表的决策风险最小化约简使得定义的约简具有更强的理论性和可解释性.

区间值决策表; 决策粗糙集; 风险最小化; 属性约简

现实生活中获得的数据集通常复杂多样,特别对于很多测量值数据,大多表现为一定范围内的连续值.对于这类数据来说,如果需要构建某种分类模型,仅依靠某一条数据判定其类别信息,不仅物理意义难以解释,而且耗费大量的时间.处理这类数据应主要考虑时间段内的整体数据特征,将一条数据单独作为一个对象的传统数据处理方式已不适合用来处理这类数据.有学者提出采用均匀时间段内的最大值和最小值来近似替代该连续区间中的所有对象,将整个数据集转换成区间值形式.

经典粗糙集理论是PAWLAK Z[1]于1982年提出的一种处理不精确、不一致、不完整数据的数学工具,已在人工智能、机器学习、模式识别等领域得到广泛应用,并获得普遍认可,成为研究热点.然而PAWLAK Z粗糙集模型所要求的条件过于严格,导致容错能力较差,并不能处理复杂的实际问题.因此,有学者将严格的等价关系变成概率包含关系,提出了概率粗糙集模型[2-6].变精度粗糙集[2](Variable Pawlak Rough Sets,VPRS)作为概率粗糙集的典型代表之一,受到了众多学者的关注.VPRS通过调整参数,大大提高了分类精度.然而对VPRS参数的语义缺乏合理的解释.YAO Y Y引入了Bayes风险理论,通过Bayes风险理论对VPRS的参数进行了解释,并给出相应的推导方法,从而提出了决策粗糙集(Decision-Theoretic Rough Sets,DTRS)模型[3].

属性约简是粗糙集理论所要研究的核心内容之一.YAO Y Y等人[7]最早对DTRS的属性约简进行了探讨,得出了DTRS约简过程中正域、负域和边界域均不具备单调性的结论;JIA X Y等人[8]指出DTRS应以风险代价作为约简的启发式因子;LI H X等人[9]定义了一种新的α-正域约简,指出约简前后的正域只需要保持非减性;MA X A等人[10]研究了决策粗糙集的多类问题;CHEBROLU S和SANJEEVI S G[11]将遗传算法引入到DTRS中,通过优化算法得到参数值;LIU J B等人[12]提出了测试代价最优下的正域属性约简算法.

上述所有的研究和方法都是基于传统的数据.而在实际生活中存在大量的区间值数据,本文将DTRS理论引入至区间值决策表中,构建区间值决策表下的DTRS模型,继而给出区间值决策表中风险损失的计算方法以及约简的定义,最后以风险损失最小化作为启发式信息提出其相应的属性约简方法.

1 区间值决策表的相关概念和性质

对于大多数区间值数据集,类别信息通常都是离散的.因此,本文讨论的是条件属性为区间值、而决策属性为离散值的情况.

定义1设有区间值决策表[13]DT=,其中C∪D表示非空有限属性集合,包括条件属性集C={a1,a2,a3,…,am}和决策属性集D={d}两部分;V=VC∪VD,其中VC表示条件属性值集合,VD表示决策属性值集合;f:U×C→VC是区间值映射,f:U×D→VD为单值映射.

表1 区间值决策

在区间值决策表中,如果采用经典粗糙集的严格等价关系,很难对论域形成合理的划分,完全取值相同的区间最大最小值才能形成一个等价类,由此得到的等价关系过于苛刻.因此,我们将相似度的概念引入区间值决策表中,用来度量区间之间的相似程度,从而采用相似关系替代严格的等价关系,增强模型的实际应用能力.

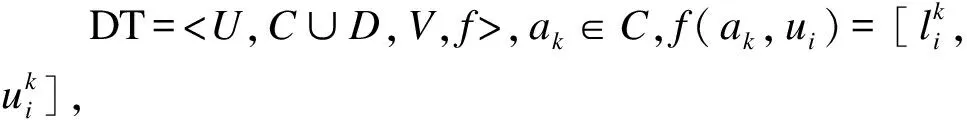
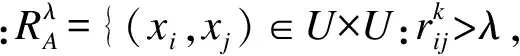
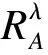
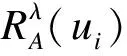
2 区间值决策表下的决策粗糙集

有了上述区间值决策表的基本概念和性质,我们可以将决策粗糙集引入至区间值决策表中,给出区间值决策表的上下近似概念.

定义4设有区间值决策表DT=,给定一参数水平λ∈[0,1],任意属性子集A⊆C,X⊆U,定义X关于A的粗糙上、下近似为:

⊄};

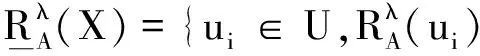
根据区间值决策表上下近似的概念,我们可以定义区间值对象子集X关于任意属性子集A的正域、负域、边界域.

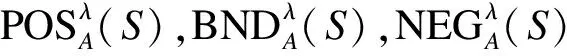
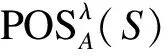
λPP≤λBP<λNP,且λNN≤λBN<λPN

(1)

令:

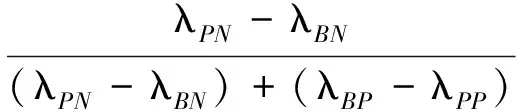
(2)

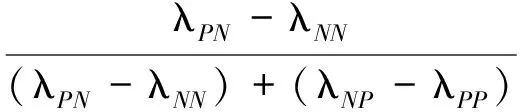
(3)

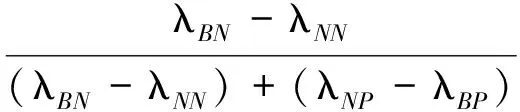
(4)

由于损失函数满足式(1)的关系,根据YAO Y Y的三支决策语义规则[3],可以推导出α∈(0,1],γ∈(0,1),β∈[0,1).

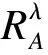
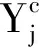
(5)

因此,我们可以推导出如下决策规则:

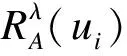
定义6设有区间值决策表DT=,给定一参数水平λ∈[0,1],对属性子集A⊆C的决策风险定义为:

由于正确分类的风险为零,即λPP=λNN=0,则有:

定义6表示区间值决策表中的决策风险应该是每个区间值对象ul在参数水平λ下根据规则划分到相应区域产生的所有风险的总和.

定义7设有区间值决策表DT=,给定一参数水平λ∈[0,1],属性子集A⊆C是C的一个决策风险最小化约简,当且仅当:

(1)A=arg(minA⊆C(CostA));

(2) ∀A′⊆A,CostA′>CostA.

在经典粗糙集下,我们对属性约简的定义基本都保持整个决策表正域不变.实际上,保持正域不变,而负域又为空集,也就相当于保证了整个决策表的边界域不变,即3个区域均不变.而在决策粗糙集中,无论正域、边界域还是负域在属性增减过程中的变化都是非单调的.通过分析发现,决策粗糙集中,每一个对象被划分的区域应该由风险决定.划分到哪一个区域的风险最小,就将该对象划到相应的区域.因此,我们应该依据风险最小化原则进行决策.同样,在区间值决策表中研究约简问题,也应以风险最小化原则为基准,计算约简时不必关注约简前后区域的变化,而应考虑区域变化后所带来的决策风险是否减小.即添加一个属性使得整个区间值决策表的决策风险总和减少,则认为该属性属于约简子集.

3 区间值决策表属性约简方法

3.1 属性重要度

条件属性子集相对于决策属性的分类能力可以通过属性重要度反映,属性重要度越高,条件属性子集对决策属性的分类能力应该越强,反之亦然.已有学者基于风险最小提出了决策粗糙集的属性约简算法.如文献[8]给出了决策风险最小化的定义,并以此作为启发式算子提出了相应的约简算法,然而该定义并没有考虑所选属性的分类能力,仅考虑了决策风险因子.文献[15]在文献[8]的基础上增加了属性重要度的概念,考虑风险代价的同时考虑到所选属性的分类能力,然而该方法仅仅考虑单个属性的重要性,并没有考虑到属性之间的强相关性.两个具有强分类能力的属性在一起并不一定能增加其分类能力.文献[16]给出了联合属性重要度的定义.以上研究均是针对传统的决策粗糙集模型,无法直接用于区间值决策表.因此,本文给出区间值决策表下的属性重要度定义.

(6)

P(u)反映的是在条件属性子集A下的λ-相容类对决策属性分类能力的大小.式(6)中取最大值是希望确定性程度最大,这样取值符合概率统计的实际意义.

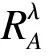
j=1,2,3,…,v,l=1,2,3,…,n

(7)

定义8表明区间值决策表中的属性重要度的计算是通过求论域中所有区间值对象的λ-相容类相对于决策的分类能力总和.即考察的对象是整个论域U,因此对每个区间值对象的条件概率P(ul)求和.

3.2 区间值决策表的决策风险最小化启发式约简算法

在现实应用中,计算约简往往采用启发式属性约简算法.相比于差别矩阵方法,虽然启发式约简只能得到一个约简结果,但可以大大地提高约简效率.启发式约简主要有前向添加,后向删除,以及两者结合3种方法.当条件属性较多时,采用后向删除法耗费大量的时间.因此,本文采用前向添加属性的方法,提出了一种区间值决策表的决策风险最小化属性约简算法(Attribute Reduction Based on Minimum Decision Cost in Interval-Valued Decision Tables).算法的主要思想是:首先根据定义8,选择属性重要度最大的一个条件属性添加到约简子集中,计算决策表的风险代价总和.在该属性基础上,计算每个属性联合该属性的整体重要度,选出重要度最大的联合属性子集,计算代价.如果添加后决策表的风险代价比未添加前的小,说明此属性可以帮助减小决策表的风险代价,同时该属性对决策具有强分类能力.反之,算法结束,得到的属性子集即为约简结果.算法描述如下.

输入:区间值决策表DT=,参数α,β,λ.

输出:属性约简集合A.

步骤1 置A=Ø.

步骤2 根据定义8和输入的λ,先计算单个条件属性ak∈C的重要度SGF({ak}),k=1,2,3,…,m,将SGF({ak})值最大的条件属性ak添加到约简集合A中(若存在多个区间值属性同时达到最大值,则选λ-相容类个数最少的属性作为ak).

步骤3 计算CostA:

(1) 计算论域U中的每个区间值对象ul的P(ul)值,l=1,2,3,…,n;

(2) 根据决策规则以及输入的α和β值将区间值对象ul划分到正域,边界域,负域中;

(3) 根据式(6)计算CostA.

步骤4 对区间值条件属性集C-A重复:

(1) 对每个区间值条件属性ak∈C-A,计算联合重要度SGF(A∪{ak});

(2) 选择SGF(A∪{ak})值最大的条件属性ak(若存在多个条件属性同时达到最大值,则将λ-相容类个数最少的属性作为ak);

(3) 令A′=A∪{ak},计算CostA′;

(4) 如果CostA′≤CostA,则A=A′;否则终止.

步骤5 最后得到的A就是区间值条件属性C相对于D的一个决策风险最小化约简.

该算法从空集开始,逐个添加区间值条件属性至约简集合中.在添加区间值条件属性时,同时考虑到已有的约简子集,保证每次添加的属性都是在现有约简子集条件下最重要的,并且保证添加该条件属性后该决策表的风险代价比未添加前的要小,即该属性的添加不会增加决策表的风险代价;否则算法结束,得到的条件属性子集A即为最终的约简结果.

4 结 论

(1) 本文给出了区间值决策表下的属性重要度计算方法,通过对每个区间值对象的条件概率P(ul)求和,得到论域中所有区间值对象的λ-相容类相对于决策的分类能力总和,符合概率统计的实际意义.

(2) 本文所提方法不仅可以保证所得到的约简集合相对于决策属性具有较强的分类能力,同时保证约简集合的决策风险最小.区间值决策表的决策风险最小化约简使得定义的约简具有更强的理论性和可解释性.

[1] PAWLAK Z.Rough sets[J].International Journal of Computer & Information Sciences,1982,11(5):341-356.

[2] ZIAKO W.Variable precision rough set mode[J].Journal of Computer and System Sciences,1993,46(1):39-59.

[3] YAO Y Y.Decision-theoretic rough set models[C]//Proceedings of the 2th International Conference on Rough Sets and Knowledge Technology.LNAI.Heidelberg:Springrt,2007:1-12.

[4] HU Q H,ZHANG L,CHEN D G,etal.Gaussian kernel based fuzzy rough sets:model,uncertainty measures and applications[J].International Journal of Approximate Reasoning,2010,51(4):453-471.

[5] SLZAK D.Rough sets and bayes factor[M]//SKOWRONA P J F.Transactions on Rough Sets.Berlin:Springer,2005:202-229.

[6] HERBERT J P,YAO J T.Game-theoretic risk analysis in decision-theoretic rough sets[C]//Proceedings of the 3th International Conference on Rough Sets and Knowledge Technology,Chengdu,China,2008:132-139.

[7] YAO Y Y,ZHAO Y.Attribute reduction in decision-theoretic roughset models[J].Information Sciences,2008,178(17):3 356-3 373.

[8] JIA X Y,LIAO W H,TANG Z M,etal.Minimum cost attributereduction in decision-theoretic rough set models[J].Information Sciences,2013,219(1):151-167.

[9] LI H X,ZHOU X Z,ZHAO J B,etal.Attribute reduction in decision-theoretic rough set model:a further investigation[C]//Proceedings of the 6th International Conference on Rough Sets and Knowledge Technology,Banff,Canada,2011:466-475.

[10] MA X A,WANG G Y,YU H,etal.Decision region distribution preservation reduction in decision-theoretic rough set model[J].Information Sciences,2014,278(10):614-640.

[11] CHEBROLU S,SANJEEVI S G.Attribute reduction in decision-theoretic rough set models using genetic algorithm[C]//Proceedings of the 2th International Conference on the Swarm Evolutionary and Memetic Computing,Visakhapatnam,India,2011:307-314.

[12] LIU J B,MIN F,LIAO S J,etal.Minimal test cost feature selection with positive region constraint[C]//Proceedings of the 8thInternational Conference on Rough Sets and Current Trends in Computing,Chengdu,China,2012:259-266.

[13] 徐菲菲,雷景生,毕忠勤,等.大数据环境下多决策表的区间值全局近似约简[J].软件学报,2014,25(9):2 119-2 135.

[14] 郭庆,刘文军,焦贤发,等.一种基于模糊聚类的区间值属性约简算法[J].模糊系统与数学.2013,27(1):149-153.

[15] 徐菲菲,毕忠勤,雷景生.基于联合属性重要度的决策风险最小化属性约简[J].计算机科学,2016,43(s1):40-43.

[16] 于洪,姚园,赵军.一种有效的基于风险最小化的属性约简算法[J].南京大学学报(自科科学版),2013,49(2):133-141.

AttributeReductionBasedonMinimumDecisionRiskinInterval-ValuedDecisionTables

XU Feifei

(SchoolofComputerScienceandTechnology,ShanghaiUniversityofElectricPower,Shanghai200090,China)

It is found that it is more reasonable when the study objects are treated as intervals than as single records in many circumstances.An attribute reduction method in interval-valued decision tables is proposed.The concept of risk in decision-theoretic rough sets is introduced into interval-valued decision tables,and the definition of decision risk is given.The corresponding reduction method is also proposed,which can not only guarantee that the obtained reduction set has stronger classification ability relative to the decision attributes,but also make sure the minimum decision risk.The defined reduction of decision risk in interval-valued decision tables is more theore-tical and interpretable.

interval-valued decision tables; decision-theoretic rough sets; minimum risk; attribute reduction

10.3969/j.issn.1006-4729.2017.05.012

2017-03-09

徐菲菲(1983-),女,博士,副教授,江西南昌人.主要研究方向为粗糙集,数据挖掘,大数据等.E-mail:xufeifei1983@hotmail.com.

国家自然科学基金(61272437,61305094);上海市教育发展基金会和上海市教育委员会“晨光计划”(13CG58);上海市自然科学基金(13ZR1417500).

TP18;TP273.24

A

1006-4729(2017)05-0471-06

(编辑 桂金星)