具有随机扰动项和混合时滞的神经网络在有限时间内的控制同步

蒲 浩, 蒋海军, 胡 成

(1. 遵义师范学院数学学院, 贵州 遵义 563006； 2. 新疆大学数学与系统科学学院, 新疆 乌鲁木齐 830046)

具有随机扰动项和混合时滞的神经网络在有限时间内的控制同步

蒲 浩1, 蒋海军2, 胡 成2

(1. 遵义师范学院数学学院, 贵州 遵义 563006； 2. 新疆大学数学与系统科学学院, 新疆 乌鲁木齐 830046)

研究一类具有随机扰动项和混合时滞的神经网络在有限时间内的控制同步. 通过李雅普诺夫稳定性理论、 随机微分方程理论、 伊藤公式以及一些不等式方法， 在p-范数下得到了新的有限时间内同步的充分条件.

随机扰动项； 伊藤公式； 神经网络； 混合时滞； 有限时间内同步；p-范数

0 引言

自从RYAN[3]提出神经网络在有限时间内稳定的理论以来， 研究者对有关神经网络在有限时间内的稳定性问题和同步问题进行了广泛的研究， 得到了很多有效的理论(详见文献[4-5]). 然而生物神经网络系统和人工神经网络系统都易受到外界的扰动， 因此研究者对具有随机扰动项的神经网络系统的稳定性问题和同步问题进行了广泛的研究[6-7]. 但是， 对于具有随机扰动项和混合时滞的神经网络在有限时间内的同步问题研究的较少.

受此启发， 本研究对具有随机扰动项和混合时滞的神经网络在有限时间内的控制同步问题进行了探讨， 通过构造一个恰当的外部控制输入Ui(t)， 得到了神经网络在有限时间内同步的充分条件. 相对于没有考虑随机扰动对神经网络在有限时间内同步影响的文章， 本研究结论更具普遍性.

1 模型和预备知识

考虑如下的具有随机扰动项和混合时滞的神经网络模型

其中:i∈I={1, 2, …,n};fj(·)表示在t时刻第j个神经原的输出量;ui(t)表示第i个神经元在t时刻的状态变量;bij、cij分别表示第i个和j个神经元之间的连接强度;hij表示第i个和第j个神经元之间的扰动时滞连结强度;τi(t)和σi(t)分别表示t时刻神经网络中的变时滞和分布时滞且满足0≤τj(t)≤τj和 0≤σi(t)≤σi;Ii表示外界对神经网络的输入量.

系统 (1)的初值条件为

ui(s)=φi(s),s∈[-τ,0] (i∈I)

对于系统(1), 我们假设:

把系统 (1) 作为主驱动系统， 为了同步, 引入如下的响应系统：

响应系统 (3) 的初值条件是

vi(s)=φi(s),s∈[-τ, 0] (i∈I)

其中:

φ(s)=(φ1(s),φ2(s), …,φn(s))T∈C([-τ, 0],Rn)；ω(t)=[ω1(t),ω2(t), ...,ωn(t)]T表示定义在具有自然滤波(Ft≥0)的完备概率空间(Ω,Ft≥0,P)上的n维布朗运动, 且有E{dω(t)}=0,E{[dω(t)]2}=dt;σij(·)表示随机扰动强度.

本研究中要通过构造一个恰当的外部输入控制Ui(t), 实现驱动系统(1)和响应系统(3)在有限的时间内同步.

其中:

定义误差系统为ei(t)=vi(t)-ui(t), 根据系统(1)和系统(3)有

2 辅助引理

引理1[8]若常数p≥2,a>0,b>0, 则不等式pap-1b≤(p-1)ap+bp,pap-2b2≤(p-2)ap+2bp成立.

为了后面主要结论证明的需要, 由引理1经过计算可知

引理3[10]若x(t)是一个关于时间t(t≥0)的n维伊藤过程, 且满足随机微分方程dx(t)=g1(t)dt+g2(t)dω(t). 若V(t,x(t))∈C1, 2(R+×Rn;R+), 则V(t,x(t))是一个实数值的伊藤过程, 且满足随机微方程

dV(t,x(t))=LV(t,x(t))dt+Vx(t,x(t))g2(t)dω(t)

其中:

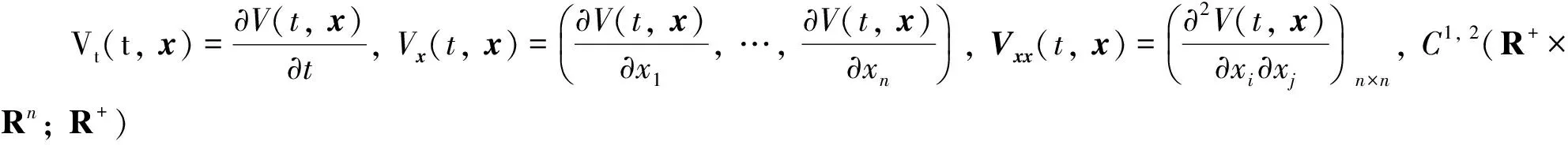
引理4如果存在实数r>0和0<λ<1, 正定连续函数V(t)满足LV(t)≤-r(V(t))λ,t≥t0则对任意给定的t0,V(t)满足下列不等式

(E(V(t)))1-λ≤V1-λ(t0)-r(1-λ)(t-t0) (t0≤t≤T)

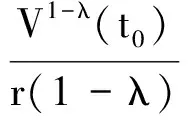
3 主要结果

证明 构造如下形式的 Lyapunov 函数

根据假设(H1)～(H2), 结合式(6)～(10), 利用引理2～4可以得到下面的式子

由引理4可知

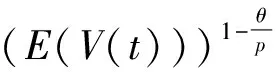
(13)

其中:

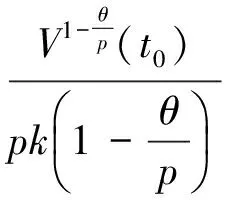
由

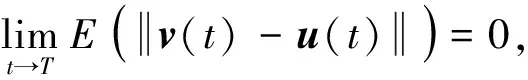
对于系统随机扰动项中的σij(t,ej(t),ej(t-τj(t)))=0时, 神经网络在有限时间内的同步问题已经被研究, 如在文[11]中作者研究了时滞神经网络在有限时间内的滞后同步. 而在本研究中考虑了随机扰动对系统在有限时间内同步的影响, 该结论更具一般性.

[1 ] LI X D, MARTIN B. Exponential synchronization of chaotic neural networks with mixed delays and impulsive effects via output coupling with delay feedback[J]. Mathematical and Computer Modelling, 2010, 52(6): 643-653.

[2] YU J, HU C, JIANG H J. Exponential synchronization of Cohen-Grossberg neural networks via periodically intermittent control[J]. Neurocomputing, 2011, 74(10): 1 776-1 782.

[3] RYAN E E. Finite-time stabilization of uncertain nonlinear planar systems[J]. Dynamics and Control, 1991, 1(1): 83-94.

[4] ABDURAHMAN A, JIANG H, TENG Z. Finite-time synchronization for memristor-based neural networks with time-varying delays[J]. Neural Networks, 2015, 69(4): 20-28.

[5] HU C, YU J, JIANG H J. Finite-time synchronization of delayed neural networks with Cohen-Grossberg type based on delayed feedback control[J]. Neurocomputing, 2014, 143(16): 90-96.

[6] DU Y H, ZHONG S M, ZHOU N,etal. Exponential stability for stochastic Cohen-Grossberg BAM neural networks with discrete and distributed time-varying delays[J]. Neurocomputing, 2014, 127(3): 44-151.

[7] GAN Q T, YANG Y Z, FAN S L,etal. Synchronization of stochastic fuzzy cellular neural networks with leakage delay based on adaptive control[J]. Differential Equations and Dynamical Systems, 2014, 22(3): 319-326.

[8] CAO J D, LIANG J L. Boundedness and stability for Cohen-Grossberg neural network with time-varying delays[J]. Journal of Mathematical Analysis and Applications, 2004, 296(2): 665-685.

[9] JIANG N, LIU X Y, YU W W. Finite-time stochastic synchronization of genetic regulatory networks[J]. Neurocomputing, 2015, 167(C): 314-321.

[10] LIU X Y, JIANG N, CAO J D,etal. Finite-time stochastic stabilization for BAM neural networks with uncertainties[J]. Journal of the Franklin Institute, 2013, 350(8): 2 109-2 123.

[11] HUANG J J, LI C D, HUANG T W,etal. Finite-time lag synchronization of delayed neural networks[J]. Neurocomputing, 2014, 139: 145-149.

Finitetimesynchronizationofneuralnetworkswithstochasticperturbationtermandmixedtimedelays

PU Hao1, JIANG Haijun2, HU Cheng2

(1. School of Mathematics, Zunyi Normal College, Zunyi, Guizhou 563006, China;2. College of Mathematics and System Sciences, Xinjiang University, Urumqi, Xinjiang 830046, China)

10.7631/issn.1000-2243.2017.05.0623

1000-2243(2017)05-0623-05

O175.1

A

2016-05-20

蒲浩(1986-)， 讲师， 主要从事微分方程研究， puhao2100@163.com

国家自然科学基金资助项目(71461027)； 贵州省科技计划课题资助项目( [2015]7053)

(责任编辑： 林晓)