不同长度基线的电离层处理策略

周 颖，满小三，李 郴

(1.61287部队，云南 昆明 650033;2.信息工程大学，河南 郑州 450001; 3.中铁四局五公司，江西 九江 332000 )



不同长度基线的电离层处理策略

周 颖1，满小三2，李 郴3

(1.61287部队，云南 昆明 650033;2.信息工程大学，河南 郑州 450001; 3.中铁四局五公司，江西 九江 332000 )

针对不同长度的基线，受双差之后电离层延迟影响不同，提出一种新的电离层处理策略。对短、中、长基线处理分别采用3种不同的数学模型：电离层固定模型，电离层加权模型，电离层浮点模型。通过3组不同长度基线实测数据处理表明，对应不同长度的基线，文中策略可以有效地提高模糊度固定率及定位精度。

电离层固定模型；电离层加权模型；电离层浮点模型；模糊度固定率

载波相位相对定位采用两台及以上的接收机进行同步观测，获取基线两端测站同步的载波相位观测值，通过组单差、双差的方法，消除大部分误差，求取载波相位观测值的整周模糊度，从而获取高精度的测量距离，使相对定位的精度可以达到厘米级至毫米级[1-4]。

对于不同长度的基线，双差之后大气延迟误差的消除程度也是不一样的，即载波相位相对定位的数学模型也不一样。如果没有采取正确的数学模型，将会导致模糊度难以固定，定位精度低。因此，必须对不同长度基线采取不同的数学模型，对流层延迟通过模型可以得到很好的改正，但是电离层难以通过模型改正，故对此有必要进行研究。对于短基线，基线长度小于15 km，双差之后电离层延迟基本被完全消除，其数学模型可以忽略电离层延迟的参数，即电离层固定模型；对于中基线，基线长度为15～100 km，但是对其双差之后电离层延迟消除的程度不确定，但是作为一个与基线长度有关的函数模型[5]，即电离层加权模型；对于长基线，基线长度大于100 km，双差差之后电离层延迟难以消除，必须作为参数实数估计及估计天顶对流层延迟，即电离层浮点模型。

本文针对不同长度基线提出3种不同的电离层延迟处理策略，采用模糊度固定率及定位精度(与已知坐标进行比较)来评估3种电离层处理策略的有效性及可靠性。

1 数学模型

1.1 函数模型

GNSS常用的双差观测方程可以表示为

(1)

GNSS码伪距与载波相对定位的双差观测方程表示为

(3)

假定基站与流动站某一历元共同观测了n颗可见卫星，选取第一颗卫星为参考卫星，且令

e=[1,1,…,1].

双差观测方程的矩阵形式

通过扩展kalman滤波估计参数X，在采用LAMBDA方法[6]解算双差整周模糊度N，获取固定解。

1.2 随机模型

Q=DRDT.

(5)

式中:R为站间单差观测量的协方差矩阵，假定选第一颗卫星为参考卫星，D为单差转双差的转换矩阵。

1.3 电离层处理策略

在进行双差之前，对对流层进行模型改正，可以很好地消除对流层延迟的影响。因此,双差之后的残留电离层延迟是主要的系统误差，影响着整周模糊度的解算及定位精度。对于不同长度基线，双差之后电离层延迟误差的消除程度也是不一样的。因此，对于不同长度的基线，考虑采用不同的电离层处理策略。

1.3.1 电离层固定模型

其随机模型没有变化。

1.3.2 电离层加权模型

对于长度为15～100 km的基线，即中基线，双差之后电离层延迟消除程度难以确定，因此，可以采用加权的方式对其进行估计。则中基线双差观测方程可以表示为

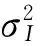
σI=l×0.99mm.

(11)

式中，l为基线的长度。

双差观测方程的协方差矩阵可以表示为

Q=DRDT.

(12)

式中:

1.3.3 电离层浮点模型

对于长度大于100 km的基线，即长基线，双差之后电离层延迟根本无法消除，因此，作为变化的参数与其他参数一起进行实时估计。则长基线双差观测方程可以表示为

其随机模型与1.3.1的随机模型一样。

1.4 模糊度固定率

整周模糊度解算是否正确直接影响相对定位的精度。而模糊度固定的性能可以通过模糊度固定率来体现，即模糊度固定率可以表示为[10]

其中:NCF表示固定的历元个数，NT表示解算的整个历元总数。因此，模糊度固定失败率为PfE=1-PSE。

2 实验分析

本文通过3组不同长度(短，中，长)基线的BDS/GPS组合相对定位来验证提出电离层处理策略，采用GPS/BDS两系统四频率兼容接收机实测长度分别为13 km，31 km，110 km的3组基线，采样间隔1 s。本文采用LAMBDA方法解算模糊度，并用Ratio值来确定模糊度的固定，设置Ratio=2。

通过图1、图2可以看出，在短基线的相对定位中，采用电离层固定模型的定位精度明显优于其余两种电离层处理策略。结合表1可以得出，采用电离层固定模型的定位精度为2～3 mm，模糊度固定率为100%，而采用其余两种电离层处理策略，定位精度反而显著降低，定位精度为7 cm左右，且模糊度固定率仅为24.1%(电离层加权模型)、26.6%(电离层浮点模型)。

图1 短基线中3种电离层处理模型定位误差的比较

图2 短基线中3种电离层处理模型Ratio值序列的比较

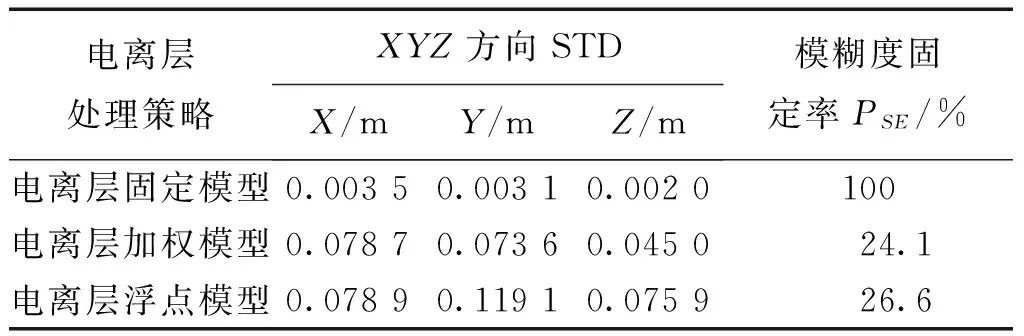
电离层处理策略XYZ方向STDX/mY/mZ/m模糊度固定率PSE/%电离层固定模型0.00350.00310.0020100电离层加权模型0.07870.07360.045024.1电离层浮点模型0.07890.11910.075926.6

在中基线的相对定位中，仅对电离层加权模型与电离层固定模型进行对比分析。通过图3、图4可以看出，对于中基线的相对定位而言，采用电离层加权模型的定位精度优于电离层固定模型。结合表2可以看出，采用前者的定位精度为7 mm左右，模糊度固定成功率为99.3%；而采用后者的定位精度为3 cm左右，模糊度固定成功率为90.4%。

图3 中基线中电离层加权模型与电离层固定模型定位误差的比较

图4 中基线中电离层加权模型与电离层固定模型Ratio值序列的比较

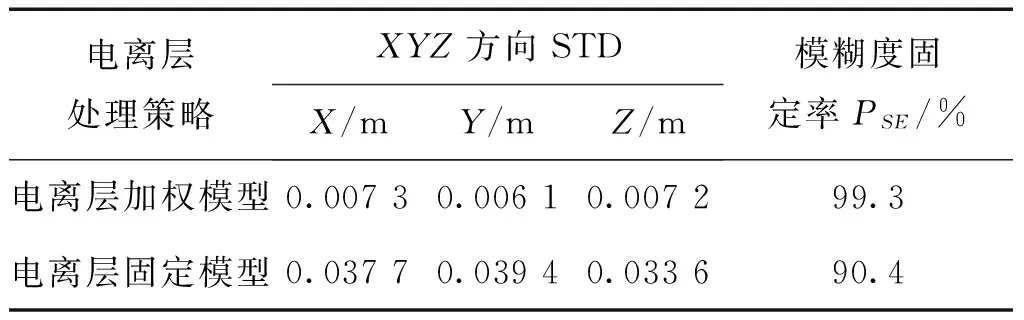
电离层处理策略XYZ方向STDX/mY/mZ/m模糊度固定率PSE/%电离层加权模型0.00730.00610.007299.3电离层固定模型0.03770.03940.033690.4

在长基线的相对定位中，同样地仅对电离层浮点模型与电离层固定模型进行对比分析。通过图5、图6可以看出，对于中基线的相对定位而言，采用电离层浮点模型的定位精度优于电离层固定模型。结合表3可以看出，采用前者的定位精度为5 cm左右，模糊度固定成功率为41.9%；而采用后者的定位精度为22 cm左右，模糊度固定成功率为23.8%。

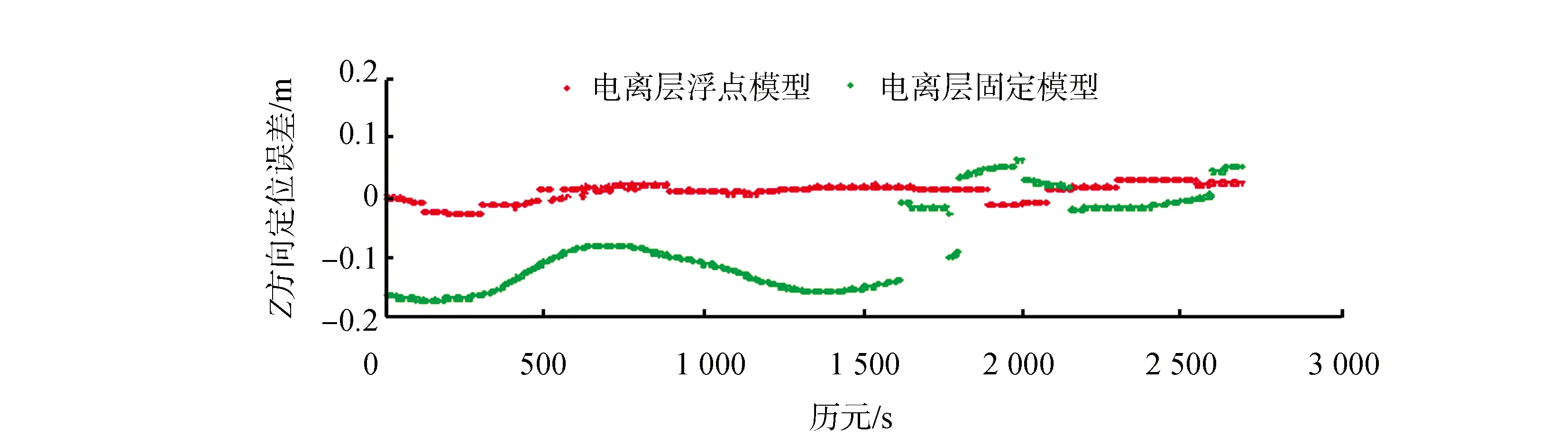
图5 长基线中电离层浮点模型与电离层固定模型定位误差的比较

图6 长基线中电离层浮点模型与电离层固定模型Ratio值序列的比较

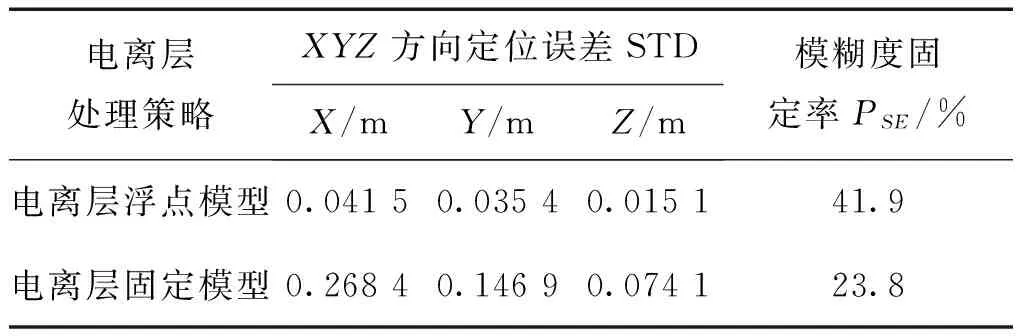
电离层处理策略XYZ方向定位误差STDX/mY/mZ/m模糊度固定率PSE/%电离层浮点模型0.04150.03540.015141.9电离层固定模型0.26840.14690.074123.8

3 结束语

对不同长度的基线受双差之后电离层残差影响的不同，对此，本文提出一种新的电离层处理策略，并推导了相关的数学模型。通过实验表明：对于短基线，采用电离层固定模型是最优的，其模糊度固定率及定位精度分别为100.00%和2 mm；对于中基线，采用电离层加权模型是最优的，其模糊度固定率及定位精度分别为99.3%和7 mm；对于长基线，采用电离层浮点模型是最优的，其模糊度固定率及定位精度分别为41.9%和5 cm。由此可知，该电离层处理策略对不同长度的基线处理效果是非常有效的，并且得出主要结论：不同长度的基线对应不同的数学模型，如果对不同长度基线采取合理的数学模型处理时，可以有效地提高模糊度固定率及定位精度。同时，如果没有采取合理的数学模型处理时，也可能会降低模糊度固定率及定位精度。

[1] 李征航，黄劲松.GPS测量与数据处理[M].武汉：武汉大学出版社，2010.

[2] 李征航，张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉：武汉大学出版社，2009.

[3] 刘基余.GPS卫星导航定位原理与方法[M].2版.北京：科学出版社，2008.

[4] 王世进,秘金钟，谷守周，等.BDS/GPS组合相对定位方法及精度分析[J].测绘通报，2014(5):1-4.

[5] ODIJK D.Fast precise GPS positioning in the presence of ionospheric delays[D].Publications on Geodesy 52,Netherlands Geodetic Commission,2002:242.

[6] TEUNISSEN P J G.The least-squares ambiguity decorrelation adjustment:a method for fast GPS ambiguity estimation[J].J geod,1995,70:65-82.

[7] ODOLINSKI R.Multi-GNSS Integer Ambiguity Resolution Enabled Precise Position[D].Curtin University,2015.

[8] 李金龙.北斗/GPS多频实时精密定位理论与算法[D].郑州：信息工程大学，2014.

[9] SCHAFFRIN B,BOCK Y.A unified scheme for processing GPS dual-band phase observations Bull[M].Geod,1988.

[10] ODOLINSKI R,TEUNISSEN P J G.An analysis of combined COMPASS/BeiDou-2 and GPS single-and multiple-frequency RTK positioning[J].Proceeding of The Institute of Navigation PNT,2013.

[责任编辑：刘文霞]

The treatment strategy of ionosphere delay with difference-lengths baseline

ZHOU Ying1,MAN Xiaosan2,LI Chen3

(1.Troops 61287,Kunming 650033,China;2.Information Engineering University,Zhengzhou 450001,China; 3.Fifth Construction Co.of China Railway Fruoth Bureau Group,Jiujiang 332000,China)

As to different-lengths baseline,differently affected by double-difference ionosphere delay,a new treatment strategy of ionosphere is proposed.Three different mathematical models are used for short,medium and long baseline: ionosphere-fixed model,ionosphere-weighted model and ionosphere-float model.The three different-lengths baseline data measured show that: this strategy can improve the ambiguity-fixed rate and positioning accuracy for different-lengths baseline.

ionosphere-fixed model;ionospheric-weighted model;ionosphere-float model;ambiguity-fixed rate

引用著录：周颖，满小三，李郴.不同长度基线的电离层处理策略[J].测绘工程，2017，26(1)：21-25，31.

10.19349/j.cnki.issn1006-7949.2017.01.005

2016-01-02

周 颖(1988-)，男,助理工程师.

P228

A

1006-7949(2017)01-0021-05