基于半参数最小二乘核估计的卫星精密钟差预报方法
徐长海,许东升
(宿州学院,安徽 宿州 234000)
基于半参数最小二乘核估计的卫星精密钟差预报方法
徐长海,许东升
(宿州学院,安徽 宿州 234000)
研究半参数最小二乘核估计模型在精密钟差预报中的应用问题,提出一种基于时间自变量差值累加的窗宽参数计算模型,并通过实验验证该模型的有效性,讨论在不同预报时间长度和已知数据量的情况下模型预报精度。实验表明,与常规模型相比,半参数最小二乘核估计模型在预报精度与稳定性方面都取得较好的效果,可以满足精密单点定位对于精密钟差预报的精度要求。研究成果对于精密单点定位技术的推广普及具有一定的促进作用。
精密钟差;半参数;最小二乘核估计;钟差预报
在精密单点定位过程中,需要用到精密钟差产品,但是由于钟差发布具有一定的延迟,且钟差的密度一般只有5 min或30 s,因此在使用过程中必须根据已有的钟差产品进行加密和预报。目前,对于钟差的预报模型一般多为一些参数模型,如二次多项式模型,它将钟差表示为时间二阶多项式函数。这类参数模型结构简单,回归结果可以外推,使用方便,但是由于回归形式固定,往往回归效果不太理想[4-9]。
半参数回归模型是20世纪80年代发展起来的一种重要的统计模型,表达了与观测值有关系参数,与观测值关系目前尚不清楚的因素用非参数回归加以处理,既保证了模型的解释能力,又获得了较好的回归精度[1-3]。
本文首先用半参数回归模型计算出二次多项式模型的三个参数和模型误差,然后用半参数最小二乘核估计对预报钟差的模型误差进行回归计算,再将本文建立模型误差计算结果与常规模型计算出的参数回归结果相加,得到精密钟差的预报值。
1 半参数回归模型[2-3]

根据参考文献[3]和[4],补偿最小二乘模型的解为
式中:S=(P+αR)-1P,S被称为光滑矩阵;I是n×n阶单位矩阵;
H=B(BTPB)-1BTP.
半参数模型估计关键的因素在于如何确定正规化矩阵R与光滑参数α,在后面的计算过程中R取相邻三观测点模型误差之差的平方和。
对于光滑参数α的计算采用Hansen and O’Leary(1993)提出的L曲线法,即当L曲线上的点αD到原点的距离为最小时的α,满足
sn2(αD)+vn2(αD)=min.
(6)
2 最小二乘核估计[3]
要利用式(1)进行钟差的外延预测计算,必须解决任意时刻tk非参数s(tk)的估计问题,选定概率密度核函数K(·)以及相应的窗宽参数h(h>0),定义tk时刻的核权函数Wi(tk)为


(8)
对于概率密度核函数K(·)以及相应的窗宽参数h(h>0)的选择对核估计性能的好坏有很大影响,核函数的种类有很多种,文中计算所采用的核函数形式为
3 算例分析
由(1)式可得精密钟差预报计算式为
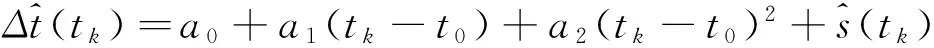
(10)
采用IGS发布的2015-09-01T00-00~2015-09-07T23 h55 min分采样密度为5 min的最终精密钟差,选择G02,G04,G14三颗卫星9月4日10时0分(为叙述方便,后面将此时刻称为边界时刻)之前的数据为已知钟差预报,9月4日10时0分之后的卫星钟差。
3.1 窗宽参数h的选择
在给定样本数据和概率密度核函数K(·)的情况下,核估计性能的好坏很大程度取决与窗宽参数的选择适当与否,窗宽参数过大或过小都会导致核估计出现问题,在此,提出了一种基于时间自变量差值累加的窗宽参数计算模型:

(11)
式中:n为已知数据个数,m为未知数据个数,用边界时刻前2 h的钟差数据作为样本,预报边界时刻之后4 h钟差,此时根据提出模型计算的窗宽参数hs=21 900,为验证该窗宽参数计算模型的有效性,分别采用不同的窗宽参数对三颗卫星钟差预报的中误差进行计算,计算结果如表1所示。

表1 不同窗宽参数钟差预报中误差 ns
从表1中可以看出,当窗宽参数选择过小时,核估计就会失效;当窗宽参数足够大时,不同窗宽参数的计算结果相差不大;模型计算出的窗宽参数有效。
3.2 预报精度与预报时长的关系
使用G14号卫星边界时刻前2 h的已知精密钟差作为样本,预报未来1 h,2 h,4 h,8 h内的钟差,计算结果如图1所示。

(a)1 h预报误差
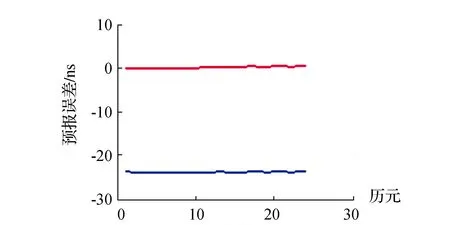
(b)2 h预报误差

(c)4 h预报误差
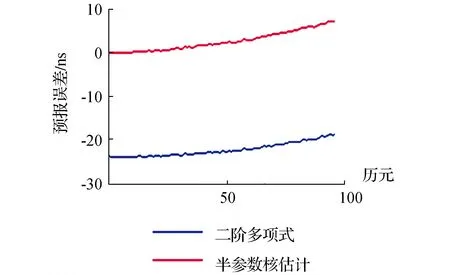
(d)8 h预报误差
从图1可以看出,二阶多项式钟差预报模型存在明显的系统误差,与之相比,半参数最小二乘核估计对于系统误差的消除效果较好,预报精度提高显著。不同预报时长计算结果如表2所示。

表2 不同预报时长计算结果 ns
从表2中的数据对比可以看出,半参数最小二乘核估计的预报精度大大高于二阶多项式,2 h内的预报精度可以达到亚纳秒级,可以满足精密单点定位对于钟差精度的要求。
3.3 预报精度与样本数据量的关系
分别采用G14号卫星边界时刻前2 h,4 h,6 h,8 h的已知精密钟差作为样本,预报未来2 h卫星钟差,计算结果如表3所示。

表3 不同已知钟差时长计算结果 ns
由表3中的计算结果可以看出,随着样本数据量的增加,两种模型的预报精度都会提高,当样本数据量增大到一定的时候,再增加样本数据量预报精度反而会下降;与二阶多项式预报模型相比,半参数核估计预报精度受样本数据量影响较小,预报精度稳定。
4 结 论
1)通过实验,文中提出的基于自变量差值累加的窗宽参数计算模型的可靠性与有效性得到了证明;
2)在小样本数据的情况下,基于半参数最小二乘核估计的钟差预报精度要高于二阶多项式预报模型;
3)基于半参数最小二乘核估计的钟差预报精度受样本数据量影响较小,预报精度稳定性好。
文中提出的窗宽参数计算模型性能只是通过实验的手段加以验证,并未从理论上证明,这是下一步需要继续研究的方向。
[1] 李政航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉: 武汉大学出版社,2009:1-24.
[2] 胡宏昌.半参数模型的估计方法及其应用[D].武汉:武汉大学,2004:7-27.
[3] 丁士俊.测量数据的建模与半参数估计[D].武汉:武汉大学,2005.
[4] 吴继忠,高俊强,李明峰.IGS精密星历和钟差插值方法的研究[J].工程勘察,2009(7):52-54,66.
[5] 潘宗鹏,柴洪洲,董冰泉,等.实时GPS精密卫星钟差估计及实时精密单点定位[J].海洋测绘,2015(5):12-15,19.
[6] 白文礼.卫星精密钟差实时确定算法研究[D].郑州:信息工程大学,2013.
[7] 陈志胜.精密卫星钟差的近实时估计[D].成都:西南交通大学,2014.
[8] 侯娟.基于半参数回归模型理论的钟差建模研究[D].北京:中国科学院研究生院(国家授时中心),2012.
[9] 冯义楷,刘焱雄,单瑞,等.GPS精密卫星钟差的计算模型研究[J].大地测量与地球动力学,2010(2):109-112.
[10] 雷雨,赵丹宁.IGS精密钟差文件的读取及加密方法[J].地理空间信息,2013(3):32-33,42.
[责任编辑:李铭娜]
Forecasting method of satellite precision clock difference based onsemi-parametric least square kernel estimating
XU Changhai,XU Dongsheng
(Suzhou University,Suzhou 234000,China)
This paper studies the application of semi-parametric least square kernel estimating model to the precision clock difference prediction,puts forward a calculation model of the window width parameter based on independent variable differential accumulation,of which the effectiveness of the proposed model is verified by experiment,and discusses the prediction accuracy cases of the different forecast time length and the amount of data given.The experimental results show that compared with the conventional model,the least square kernel estimating model is good in accuracy prediction and stability,which can meet the accuracy requirement of precise point positioning for the precision clock difference prediction.The research for the precise point positioning technologies has a certain reference.
precision clock offsets;semi-parameter;least square kernel estimating;clock difference prediction
引用著录:徐长海,许东升.基于半参数最小二乘核估计的卫星精密钟差预报方法[J].测绘工程,2017,26(1):61-63,68.
10.19349/j.cnki.issn1006-7949.2017.01.013
2016-01-05
安徽省教育厅自然科学资助项目(KJ2012Z392);宿州学院硕士科研启动基金资助项目(2010YSS07)
徐长海(1983-),男,硕士.
P228
A
1006-7949(2017)01-0061-03

