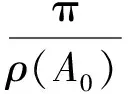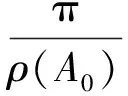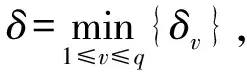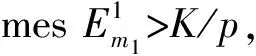一类复微分方程无穷级解的角域测度及Borel方向
王金莲,闵小花,易才凤
(1.江西师范大学学报杂志社,江西 南昌 330022;2.江西师范大学数学与信息科学学院,江西 南昌 330022)
一类复微分方程无穷级解的角域测度及Borel方向
王金莲1,闵小花2,易才凤2
(1.江西师范大学学报杂志社,江西 南昌 330022;2.江西师范大学数学与信息科学学院,江西 南昌 330022)
运用亚纯函数的Nevanlinna理论及整函数的相关理论,研究了复方程f(k)+Ak-1f(k-1)+…+A1f′+A0f=0的无穷级解的角域测度及Borel方向.
微分方程;无穷级;测度;亏值;Borel方向
0 引言和主要结果
本文采用亚纯函数Nevanlinna值分布理论的标准记号.[1-2]记亚纯函数f(z)在整个复平面上的增长级为ρ(f),此外,令0<β-α≤2π,记
Ω(α,β)={z|α
其增长级为
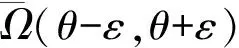
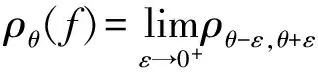
另外,应用文献[3]给出的如下定义:假设f(z)是ρ(0<ρ<∞)级整函数,对于某个固定的θ,若ρ(θ)=ρ,则称Lθ:argz=θ为f(z)的1条ρ级射线,且ρ级射线充满的角域称为f(z)的ρ级射线角域(由文献[3]可知f(z)的ρ级射线角域不会退化为1条射线).
G.G.Gunderson等人指出:若A(z)和B(z)为有限级整函数且满足ρ(A)<ρ(B),则2阶微分方程
f″+Af′+Bf=0
(1)
的每个非零解f均为无穷级.在此基础上,周志进等[4]考虑了当方程(1)的所有非零解f均为无穷级时,以原点为始点的无穷级射线角域问题,得到了:
定理A假设A(z)和B(z)是有限级整函数且ρ(A)<ρ(B)(1/2≤ρ(B)<∞),则使得方程(1)的每个非零解f为无穷级的θ,满足mes(θ|ρθ(f)=∞)≥π/ρ(B),其中θ是由原点出发的射线的辐角,即满足argz=θ(0≤θ<2π).
定理B假设A(z)和B(z)是有限级整函数且ρ(A)<ρ(B),其中B(z)具有有限条Borel方向和q个有穷亏值.则使得方程(1)的每个非零解f为无穷级的θ满足mes(θ|ρθ(f)=∞)≥qπ/ρ(B).
关于高阶微分方程
f(k)+Ak-1f(k-1)+…+A1f′+A0f=0,
(2)
陈宗煊等[5]证明了结果:若Ai(z)(i=0,1,…,k-1)是整函数且ρ(Ai)<ρ(A0),则方程(2)的所有非零解f均为无穷级.关于方程(2)的无穷级解的讨论还有不少结果,如文献[6-12]等.本文研究的问题是:当方程(2)的每个非零解f为无穷级时,以原点为始点无穷级射线的角域测度究竟有多大.另外,受文献[13-14]关于方程(1)的无穷级解的Borel方向研究的启发,还讨论了无穷级解的Borel方向,证明了下面2个定理.
定理1假设Ai(z)(i=0,1,…,k-1)是有限级整函数,且
ρ(Ai)<ρ(A0)(1/2<ρ(A0)<∞;i=1,2,…,k-1),
则使得方程(2)的每个非零解f为无穷级的θ(0≤θ<2π)满足
mes(θ|ρθ(f)=∞)≥π/ρ(A0),
并且对任意的θ0∈{θ|ρθ(f)=∞},由原点发出的射线Lθ0:argz=θ0均为f的无穷级Borel方向.
另外,当条件改为ρ(Ai)<ρ(A0)(0<ρ(A0)≤1/2;i=1,2,…,k-1),或者Ai(z)(i=1,…,k-1)是多项式,A0(z)是零级超越整函数时,则方程(2)的每个非零解f沿径向Lθ:argz=θ(∀θ∈[0,2π))的增长级ρθ(f)=∞,并且复平面内由原点发出的射线均为f的无穷级Borel方向.
定理2假设Ai(z)(i=0,1,…,k-1)是有限级整函数,
ρ(Ai)<ρ(A0)(i=1,…,k-1;1/2<ρ(A0)<∞),
并且A0(z)具有p(0 引理1[3]若f(z)是级为ρ(1/2≤ρ<∞)的整函数,那么f(z)至少存在1个ρ级射线角域,并且每个ρ级射线角域的开度不小于π/ρ. 注1若ρ=0.5,则至多除去一条例外,复平面内由原点发出的射线均是f(z)的ρ级射线. 的θ具有正测度,则方程(2)的每个非零解f满足ρα β(f)=∞. 引理3[7]设f(z)是复平面上的无穷级亚纯函数.则由原点出发的射线argz=θ为f(z)的1条无穷级Borel方向的充要条件是∀ε>0,都有ρθ-ε,θ+ε(f)=∞. 引理4[13]设f(z)为ρ(0<ρ<1/2)级整函数,则复平面内由原点发出的射线均为f(z)的ρ级射线. 成立的φ(0≤φ<2π)值构成的集合Ejv的测度mesEjv>K(δ,q,ρ)>0,这里K(δ,q,ρ)是仅依赖于δ,q,ρ的正数. log|f(Rjeiφ)-a0|<-ηU(Rj) 的φ(0≤φ<2π)构成的集合Ej的测度大于正数K′(不依赖于j),则对于充分小的正数α和大于1的正数Q(Q<1/4α),当j充分大时,在区域Dj:(Rj/Q≤|z|≤QRj)∩(φ1+10α≤argz≤φ2-10α)上,有 mesE{φ|φ1<φ<φ2,log|f(Rjeiφ)-a1|<-ηU(Rj)}>K′, mesE{φ|φ3<φ<φ4,log|f(Rjeiφ)-a2|<-ηU(Rj)}>K′ 成立,则φ3-φ2≥π/ρ,(φ1+2π)-φ4≥π/ρ. 引理8[3]若f(z)为ρ(0<ρ<∞)级整函数,Lθ:argz=θ是f(z)的任意ρ级射线角域的1条边界,则Lθ必为f(z)的1条ρ级Borel方向. 引理9[3]有穷正级整函数f(z)的ρ级Borel方向必位于f(z)的ρ级射线角域内部或边界上. 引理10[3]设整函数f(z)的级ρ>1/2,并且f(z)的某一ρ级射线角域G内没有ρ级Borel方向,则G的开度必为π/ρ. 由于ρ(Ai)<ρ(A0)(i=1,…,k-1),则∀K>0及∀θ∈(α,β),有 另外,若0<ρ(A0)≤1/2,则由注1及引理4,并运用类似于上面的证法以及整函数沿径向上的增长级的定义,即可知方程(2)的每个非零解f沿径向Lθ:argz=θ(∀θ∈[0,2π))的增长级ρθ(f)=∞. 若Ai(z)(i=1,…,k-1)是多项式,A0(z)是零级超越整函数,也用类似于上面的证法可得方程(2)的每个非零解f沿径向Lθ:argz=θ(∀θ∈[0,2π))的增长级ρθ(f)=∞. 由引理3知在以上2种情形下,复平面内由原点发出的射线均为f的无穷级Borel方向. 对A0(z),取α使得0<α 再次运用引理6, 则在弧段{Rjeiφ|φm2+10α≤φ≤φm2+1-10α}上有 且根据引理7知G1与G2不会相邻.类似于上面的证明, 在G1∪G2内, 下列集合 从而由最大模原理可知A0(z)在每个角域Gv内有界,再由引理7知,由上述q个角域Gv的边界所构成的另外的q个角域Ωv(v=1,2,…,q)的开度都不小于π/ρ(A0).由引理8和引理9,这q个角域Ωv(v=1,2,…,q)都是A0(z)的ρ(A0)级射线角域.再由ρ(Ai)<ρ(A0)(i=1,…,k-1),则在A0(z)的每个ρ(A0)级射线角域Ωv(v=1,2,…,q)内类似于定理1的证明并运用引理2,即可证明使得方程(2)的每个非零解f为无穷级的θ,满足mes(θ|ρθ(f)=∞)≥qπ/ρ(A0).特别地,当p=2q时,由引理10可知这q个角域Ωv(v=1,2,…,q)的开度都等于π/ρ(A0),所以在这种情形下上式取等号. 最后,由引理3可知,∀θ0∈{θ|ρθ(f)=∞},由原点发出的射线Lθ0:argz=θ0均为f的无穷级Borel方向. [1] HAYMAN W K.Meromorphic functions [M].Oxford:Clarendon Press,1964:1-190. [2] 杨乐.值分布及其新研究 [M].北京:中国科学出版社,1982:1-230. [3] 戴崇基,嵇善瑜.ρ级射线及其Borel方向分布间的关系 [J].上海师范大学学报(自然科学版),1980(2):16-24. [4] 周志进,伍鹏程,龙见仁.关于复微分方程f″+Af′+Bf=0具有无穷级解的角域测度 [J].贵州师范大学学报(自然科学版),2013(2):50-53. [5] CHEN ZONG XUAN,GAO SHI AN.The complex oscillation theory of certain non-homogeneous linear differential equations with transcendental entire coefficients [J].J Math App,1993,179:403-416. [6] 龚攀,肖丽鹏.某类高阶复微分方程解的增长性 [J].江西师范大学学报(自然科学版),2014,38(5):512-516. [7] 廖良文.非线性复微分方程研究的新进展 [J].江西师范大学学报(自然科学版),2015,39(4):331-339. [8] 徐俊峰,仪洪勋.高阶线性微分方程解的角域增长性 [J].系统科学与数学(自然科学版),2008,28(6):702-708. [9] 石磊,伍鹏程,龙见仁.亚纯函数的Borel方向 [J].贵州师范大学学报(自然科学版),2012,30(3)55-59. [10] 戴崇基.关于整函数ρ0阶射线的个数 [J].华东师范大学学报(自然科学版),1979(3):30-33. [11] 王金莲,艾丽娟,易才凤.一类线性微分方程解的增长性 [J].陕西师范大学学报(自然科学版),2016,44(6):14-18. [12] 涂鸿强,刘慧芳.一类2阶线性微分方程的增长性 [J].江西师范大学学报(自然科学版),2017,41(2):184-188. [13] 刘旭强,易才凤.方程f″+Af′+Bf=0的解在角域内的增长性及Borel方向 [J].江西师范大学学报(自然科学版),2013,37(1):1-5. [14] 胡军,易才凤.高阶非齐次线性微分方程解沿径向的振荡性质 [J].江西师范大学学报(自然科学版),2014,38(2):162-166. TheangularmeasureandBoreldirectionofinfiniteordersolutionsofaclasscomplexdifferentialequations WANG Jin-lian1,MIN Xiao-hua2,YI Cai-feng2 (1.Periodical Office of Journal,Jiangxi Normal University,Nanchang 330022,China;2.College of Mathematics and Informatics,Jiangxi Normal University,Nanchang 330022,China) It was investigated that the angular measure and Borel direction of infinite order solutions of linear differential equationsf(k)+Ak-1f(k-1)+…+A1f′+A0f=0 by using the Nevanlinna theory and the correlation theory of entire function. differential equation;infinite order;measure;deficient value;Borel direction 1000-1832(2017)04-0020-05 10.16163/j.cnki.22-1123/n.2017.04.005 2016-09-28 国家自然科学基金资助项目(11171170). 王金莲(1963—),编审,主要从事复分析和编辑学研究. O 174学科代码110·34 A (责任编辑:李亚军)1 几个引理
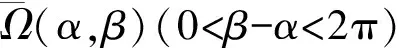
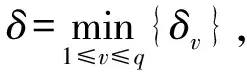
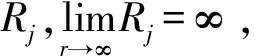
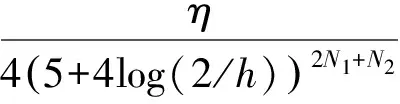
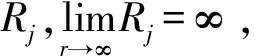
2 定理的证明