基于GLC30数据的斑块级别景观指标适用性及简化研究

张倩宁， 谭诗腾,2， 徐 柱,2,3， 黄泽纯,2

(1.西南交通大学地球科学与环境工程学院，成都 611756； 2.高速铁路运营安全空间信息技术国家地方联合工程实验室，成都 610031； 3.教育部轨道交通安全协同创新中心，成都 610031)

基于GLC30数据的斑块级别景观指标适用性及简化研究

张倩宁1， 谭诗腾1,2， 徐 柱1,2,3， 黄泽纯1,2

(1.西南交通大学地球科学与环境工程学院，成都 611756； 2.高速铁路运营安全空间信息技术国家地方联合工程实验室，成都 610031； 3.教育部轨道交通安全协同创新中心，成都 610031)

斑块是景观格局的基本组成单元，斑块级别指标是量化研究斑块形态的重要基础。目前斑块描述指标冗余纷杂,因此拟对现有的斑块级别指标进行分析，指出指标本身的适用性，并利用相关性分析和主成分分析方法实现斑块级别形态描述指标的综合和简化。在对11个斑块级别指标进行适用性分析的基础上，采用30 m空间分辨率全球地表覆盖类别数据(GLC30)进行实验，利用2种分析方法对除面积和周长外的9个复合指标进行了简化分析。实验结果表明，回旋半径和支撑半径这2个指标可以在较大程度上区分斑块形态。本文研究方法和实验结果为量化研究景观格局尺度效应积累了经验。

GLC30； 景观格局指标； 斑块； 主成分分析； 相关性分析

0 引言

景观生态学中景观格局指标是定量化研究景观格局的重要因素，景观格局指标能够高度浓缩景观格局信息，是反映景观结构组成以及空间配置特征的简单量化指标[1-5]。目前，景观格局指标的适用性及相关性、认识景观格局指标与景观格局之间的关系是研究景观格局多尺度表达的核心问题。当前景观格局分析中有上百个景观指数，且由于景观数据属性、指标本身性质以及应用场景等原因，景观格局指数在应用当中存在一定的局限性。如何根据研究目的和研究对象的特点正确选择景观指数是一个普遍存在、尚未完善、亟待解决的问题[6-9]。因此，开展此项研究具有重要的理论和现实意义。

Riitters等[10]分析了55个景观格局指标间的相关性，得出景观格局在很大程度上可由26个指标来表示，同时对这26个指标进行了主成分分析，最终简化为平均斑块紧凑度、纹理、平均斑块形状、斑块周长-面积尺度演变、属性类别数量和大斑块密度-面积尺度演变共6类指标，这6类指标相应地可简化为6个单变量指标来表示； 布仁仓等[11]分析了39个景观格局指数的相关性； 彭保发等[12]从景观类型组成、斑块特征和景观异质性3个方面分析了景观格局特征，其中斑块特征主要通过斑块规模、形状指数和分维度等来反映，并指出斑块形态对于景观格局稳定性有一定的影响； 彭建等[13]探讨了土地利用分类系统中的景观格局指数的分类，并根据景观格局指数对土地利用类型数目变化响应的可预测性，将其分为随土地利用变化可预测性强的指数、可预测性差的指数以及两者间无规律而言的指数3类； Lechner等[14]对景观格局指标与分类精度以及地理空间处理方法之间的关系进行了研究，指出景观格局指标受景观格局及处理方法的影响。综上所述，Riitters等从宏观角度上分析了景观格局指标，但并未针对某一特定类型的景观格局指标进行进一步研究； 而其他很多学者只是利用景观格局指标分析景观结构及发展进程。目前学者们仍缺乏对基于某一个类型的景观指标的研究。McGarigal等[15]认为景观格局可从斑块、类别和景观3个级别来进行描述和分析。斑块是组成景观格局的基本单元，本文拟对斑块级别景观指标进行解释和分析，为进一步研究类别和景观级别的景观格局尺度效应提供参考依据。

一般来说，在众多指标中，可以选取一组或者几组具有代表性且冗余程度低的指标来表示景观格局及结构[16]。同理，斑块信息也可由几个代表性指标来表达。针对以上问题，本研究的目标旨在描述斑块指标的适用性，进而选取一组或者多组具有代表性的斑块指标来描述斑块信息，以简化斑块指标的使用复杂度。研究主要解决以下3个问题： ①斑块级别景观格局指标的适用性及其局限性； ②最少需要几个指标在很大程度上实现斑块形态信息的描述及表达； ③优选指标或者指标组合来实现斑块形态信息的最佳表达。

1 研究方法

1.1 斑块级别指标适用性分析

根据指标是否具有空间属性，景观格局指标一般可分为合成指标和空间特征指标。其中合成指标主要用于描述类别、丰富度等非空间信息； 空间特征指标包含斑块面积、边缘长度、斑块形状复杂度、核心面积、斑块破碎度和斑块隔离度等指标。描述斑块信息的景观格局指标众多，本文的研究目标主要是对斑块形态指标进行多指标分析和评价。

根据McGarigal等[15]在景观格局分析软件Fragstats中对景观格局指标的描述，本文选取了7个和斑块形态有关的指标来做多指标综合评价，分别为斑块面积、斑块周长、回旋半径、周长-面积比率、形状指数、分形维数和关联外接圆。

景观格局分析中，学者通常还会采用其他指标描述斑块形态。本文还选取了填充度、面积-周长比率[17-20]和紧凑度[21]3个斑块形态指标参与多指标分析评价。

为了更好更全面地描述斑块的形态，本文提出了一个新的指标——支撑半径。支撑半径为与斑块周长和面积相同的矩形的宽度，该指标能够很好的刻画斑块的平均宽度，公式为

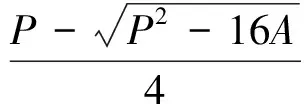
(1)

式中：Rs为斑块的支撑半径；P为斑块的周长；A为斑块的面积。

在斑块随尺度演变过程中，研究发现目标尺度下，斑块的存在与否和斑块的平均宽度即支撑半径有一定的关系，当斑块的支撑半径远远大于目标尺度下的分辨率时，斑块在尺度演变过程中将会被保留； 当支撑半径远远小于目标尺度下的分辨率时，斑块在尺度演变过程中会消失； 而当斑块的支撑半径与目标尺度的分辨率相当时，斑块在尺度演变过程中存在与否将变得不确定。

本文选取以上11个斑块级别空间形态指标进行多指标分析及评价。这11个斑块形态指标的详细描述、说明及局限性见表1。

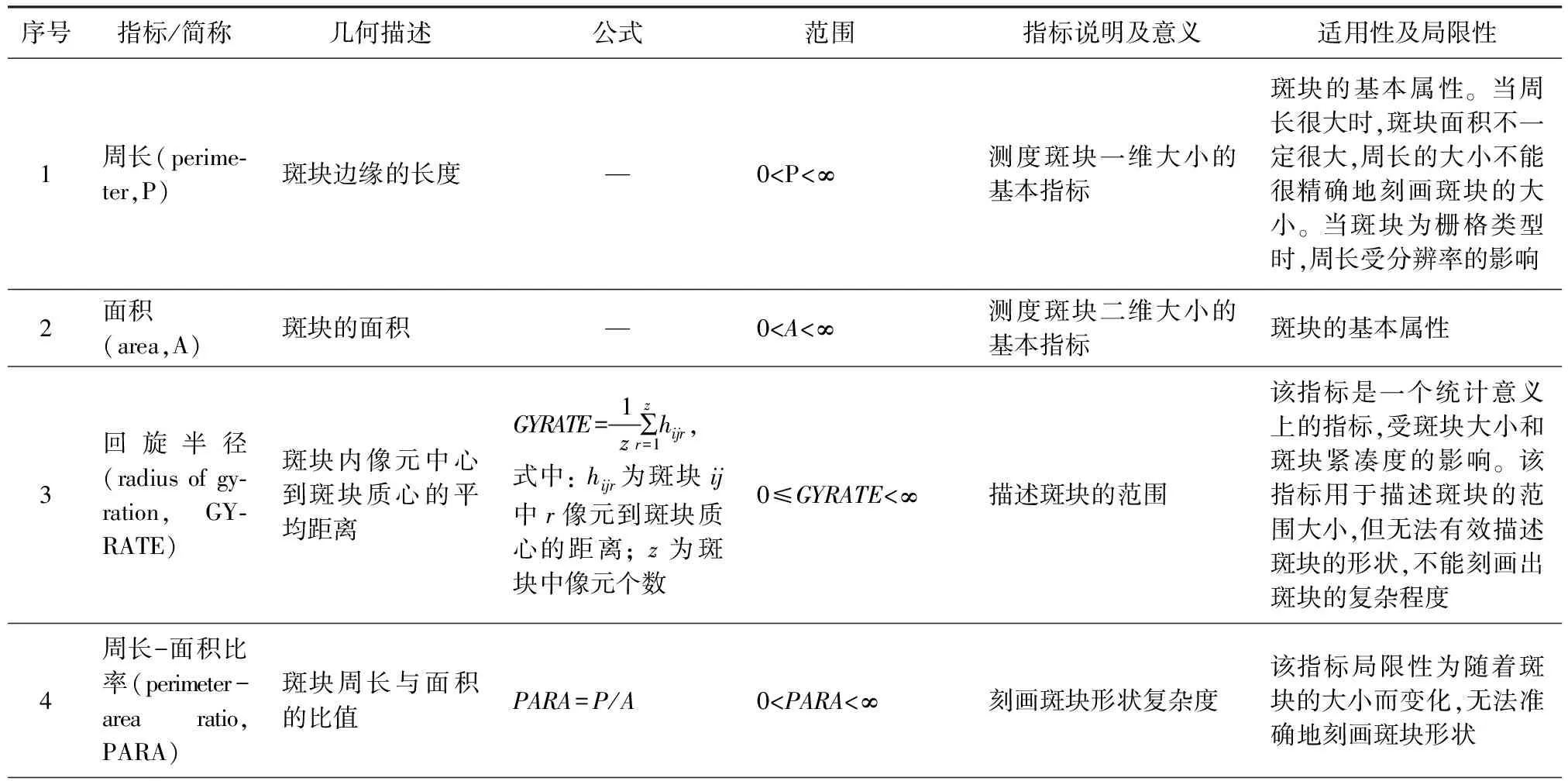
表1 斑块形态指标解释及局限性描述Tab.1 Description and explanation of the patch morphology metrics

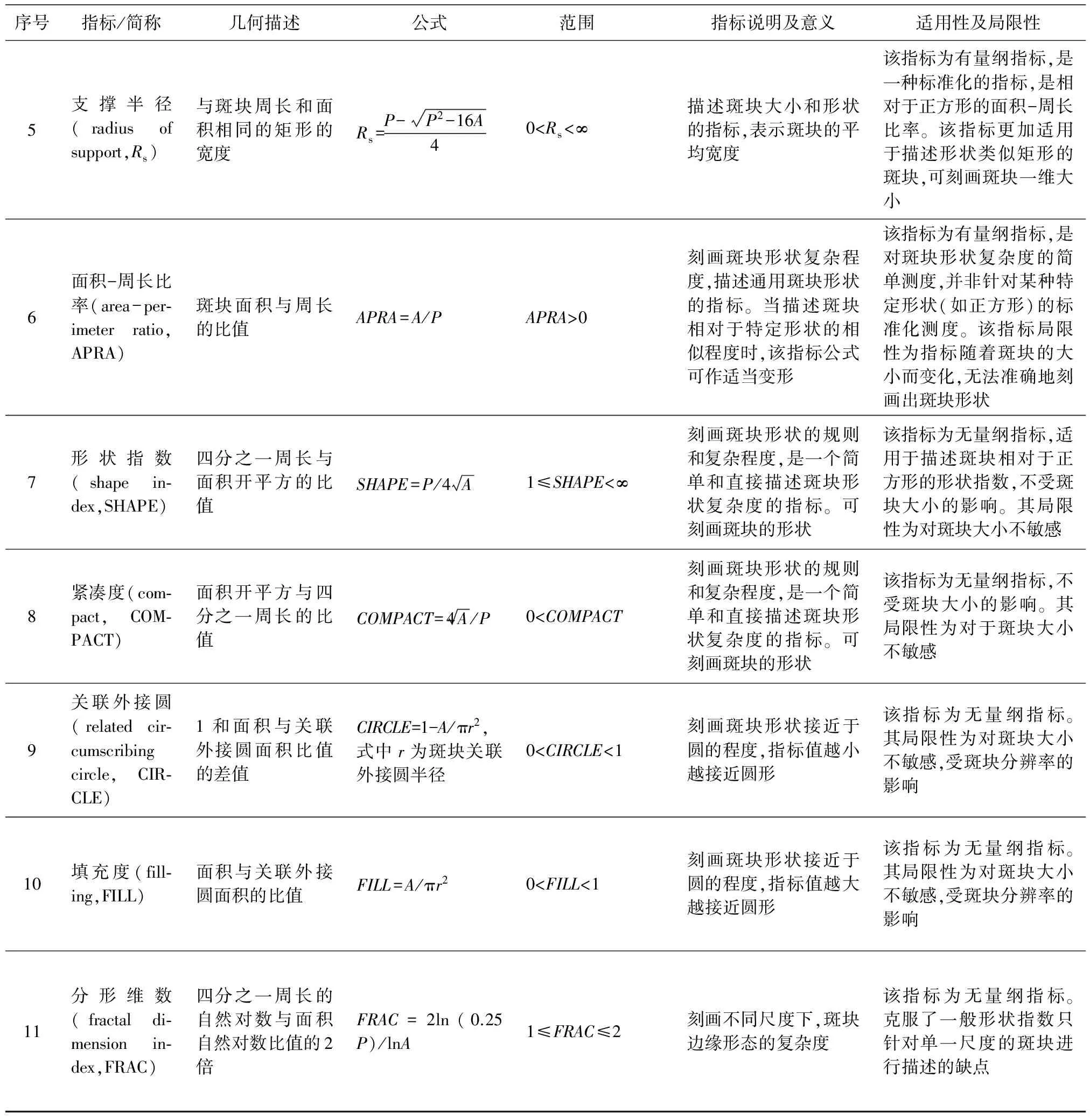
续表

1.2 分析方法

本文的研究目标是对斑块级别指标进行多指标综合评价。在统计学中，主成分分析法是一种对多指标综合评价的定量分析方法[22]。主成分分析方法的原理是对于最初参与分析的所有变量，在尽可能保持原有信息的基础上，将具有重复信息的变量去除，保留尽可能少的两两互不相关的新变量。然而在分析过程中，主成分分析方法对于数据中指标间的高度相关性及量纲十分敏感[22]。据1.1小节可知，这11个斑块级别指标的量纲是不一致的，同时指标间也可能存在一定的相关性，因此在进行分析之前，需对实验数据作相关性分析以及量纲统一化处理。

相关性分析是用来刻画指标间的相关程度，此处采用的是皮尔森相关系数r，该相关系数是一个用来反映2个变量线性相关程度的统计量，r的取值范围为(-1,1)，r的绝对值越接近1表示相关性越强。

标准化方法可根据数据自身的特点进行选择。常用的标准化方法有均值法[23]和Z-Score法[23-25]。采用Z-Score法对数据进行标准化后，各指标的均值为0，方差为1，这样会导致数据部分信息损失,即丢失各指标间变异系数上的差异； 而均值法可保持数据中各指标的变异系数不变[23]。因此本实验中采用均值法进行标准化，进一步采用协方差分析法开展主成分分析。其中，均值法标准化方法公式为

(2)

式中：Y为标准化后指标值；X为原始指标值；Xm为原始指标均值。

主成分分析中，某个主成分分量对应的特征值越大，说明该主成分分量包含的方差信息越多，对应该主成分分量的贡献率就越大。

本文采用OriginPro2015软件中的Statistics工具实现指标间的相关性分析及主成分分析。

1.3 验证方法

以斑块识别度(identification degree)作为评价斑块形态指标组合优劣的标准，验证本文选取斑块形态指标值的有效性。斑块识别度公式为

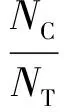
(3)

式中：I为斑块识别度；NC为所有斑块中不同斑块指标组合的数目；NT为所有斑块数目。

2 实验分析

2.1 实验设计

首先，获取全球30 m空间分辨率地表覆盖类别数据，选取面积相同但景观格局各异的实验区； 其次基于地表覆盖类别数据提取实验区的斑块数据，对斑块数据进行预处理，剔除像元数小于6个的斑块，此时得到符合要求的实验斑块数据。接下来，计算实验斑块数据的斑块形态指标值，对各指标进行主成分分析和指标间相关性分析，筛选出较大程度上能够描述和表示斑块形态的指标。实验设计如图1所示。

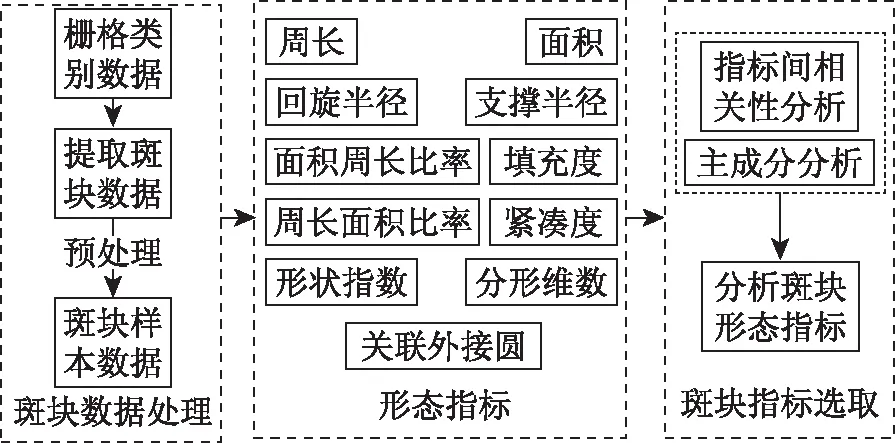
图1 实验设计图Fig.1 Experimental design char

2.2 实验结果及分析

2.2.1 实验数据

地表覆盖类别数据使用的是国家基础地理信息中心提供的30 m空间分辨率全球地表覆盖数据(GLC30，http: //www.globallandcover.com)，实验区范围为中国四川省。在实验区内选取了3个面积相同、形状一致，但景观格局各异的实验区域。在实验区域P1景观格局中，包含6种地表覆盖类别，分别为耕地、森林、草地、水体、湿地以及人造覆盖，其中森林、草地和水体3种类别所占面积较大； 从P1中共提取有效斑块1 464个，其斑块的面积较大。在实验区域P2景观格局中，包含7种地表覆盖类别，分别为耕地、森林、草地、灌丛地、水体、湿地以及人造覆盖，其中人造覆盖和耕地2种类别所占面积较大； 从P2中共提取有效斑块15 366个，其小斑块相对较多，斑块面积较小，斑块形态较复杂。在实验区域P3景观格局中，地表覆盖类别较多，包含了10种地表覆盖类别，分别为耕地、森林、草地、灌丛地、水体、湿地、苔原、人造覆盖、裸地以及多年积雪或冰； 从P3中共提取有效斑块29 861个，各类别斑块十分破碎，且覆盖面积很小。实验区域地表覆盖类别见图2。

2.2.2 斑块指标相关性分析

面积是最基本的景观指数,决定了景观总边界长度、斑块数和类型密度等基本指数,同时与多个指数有显著的相关关系(相关系数绝对值大于0.75)[7]，周长同理。于是在进行相关性分析和主成分分析时去除面积和周长指标，对余下的9个指标进行简化分析。实验首先对基于3个实验区域计算的9个斑块指标值进行相关性分析，相关性系数计算结果分别见表2—4。在进行主成分分析之前，先去除相关性较高的指标。当指标间相关系数大于0.9时，认为指标互相高度相关，此时在2个指标中选取其中一个作为主成分分析的分量。从表2—4中可以看出，FILL与CIRCLE完全负相关，由于FILL对于斑块的描述更加直观，当FILL值越小时，说明斑块形态越离散； 反之，斑块形态则聚集且更加偏向于圆形，因此选取FILL指标作为主成分分析的分量；Rs与APRA高度相关，APRA是斑块面积与周长比值的一般形式，并非相对于特定形状的描述指标，而Rs是斑块相对于规则形状矩形的描述指标，本研究中采用的数据是地表覆盖类别数据，地表覆盖类别数据的最小单元是正方形的像元，因而此处选用Rs以更加准确地刻画斑块形态；FRAC与COMPACT高度相关，由于指标COMPACT与SHAPE互为倒数，在一定程度上，可以用SHAPE来代替COMPACT，因而此处选取指标FRAC作为主成分分析的分量。综上，3个实验区域的主成分分析指标均为GYRATE,Rs,PARA,SHAPE,FILL和FRAC。

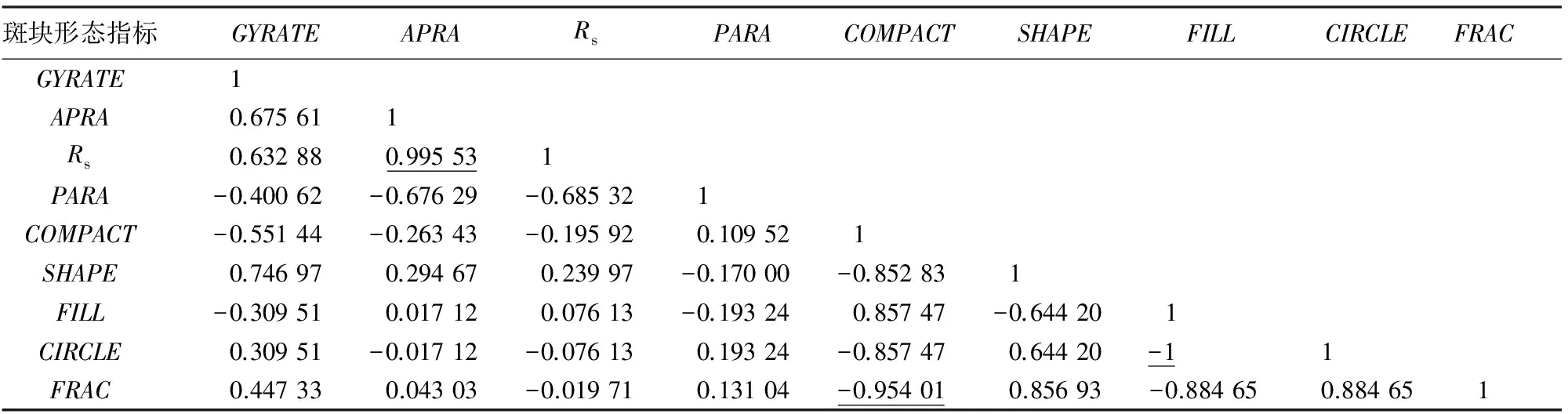
表2 实验区域P1斑块形态指标间相关系数Tab.2 Correlation coefficient of patch morphology metrics in experimental area P1

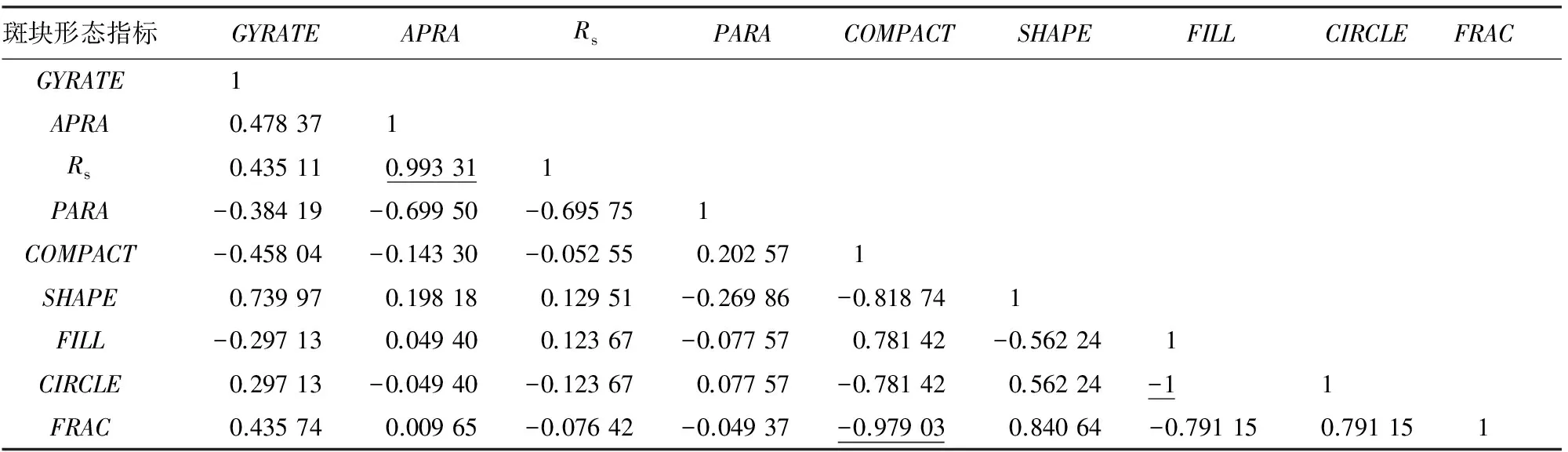
表3 实验区域P2斑块形态指标间相关系数Tab.3 Correlation coefficient of patch morphology metrics in experimental area P2

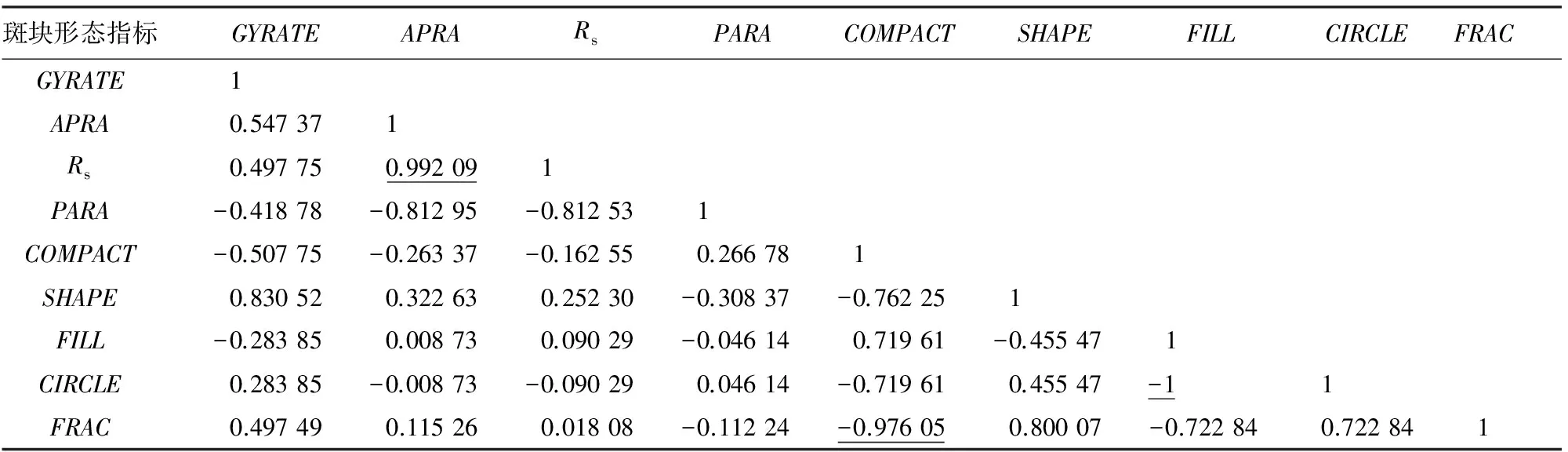
表4 实验区域P3斑块形态指标间相关系数Tab.4 Correlation coefficient of patch morphology metrics in experimental area P3

2.2.3 斑块指标主成分分析

基于GYRATE,Rs,PARA,SHAPE,FILL和FRAC这6个指标，对3个实验区域数据做主成分分析，筛选出能够有效表达斑块形态的指标个数以及最佳指标。

对去除相关性后的6个指标进行主成分分析，各主成分分量的特征值及累计贡献率见表5。当主成分分量的累积贡献率超过85%时，认为这几个主成分分量可以表示原始数据的大部分信息。从表5可以看出,实验区域P1，P2和P3数据的前2个主成分分量的累积贡献率分别为94.26%，94.50%和95.52%，累积贡献率均大于85%。由此说明，P1,P2和P3这3组斑块数据均可由前2个主成分分量来描述和表示。对去除相关性后的6个指标进行主成分分析，3个实验区域的各指标在主成分分量1和2中的系数见图3—5。

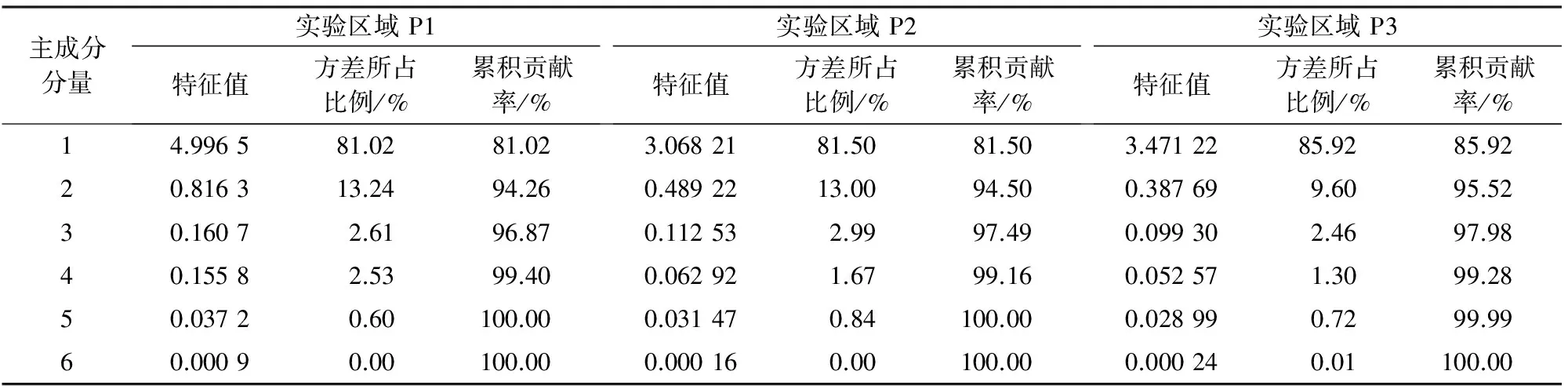
表5 实验区域主成分分量特征值及累计贡献率Tab.5 Principal component eigenvalues and cumulative contribution rate in experimental area

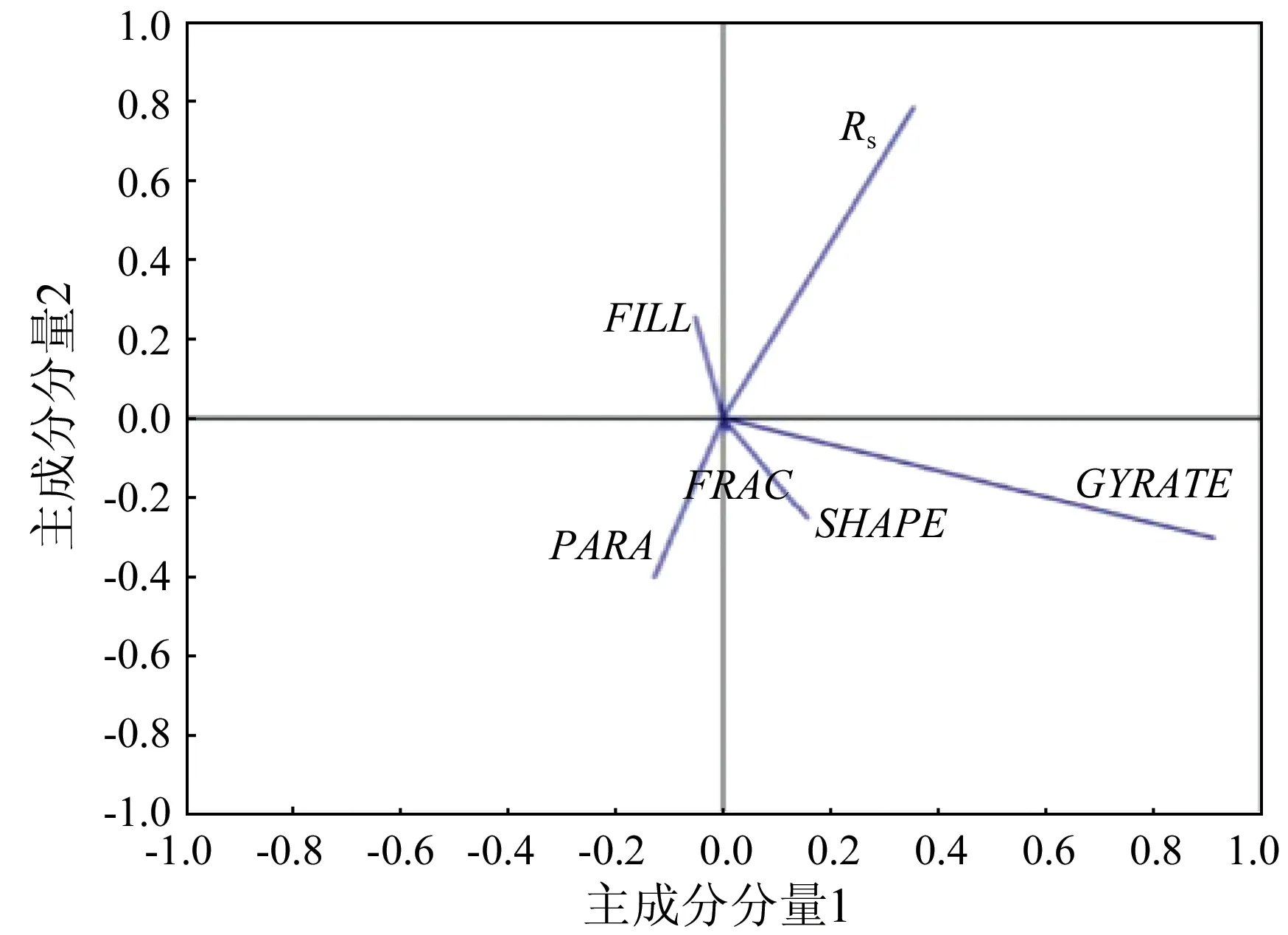
图3 实验区域P1各指标在前2个主成分的载荷图Fig.3 Loading plot of six metrics in P1

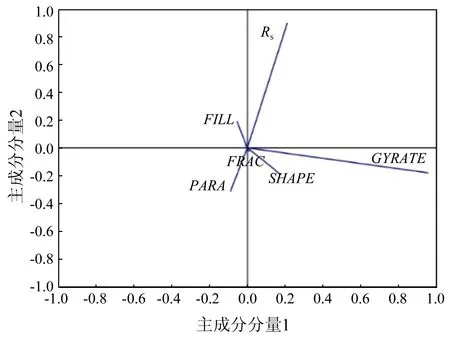
图4 实验区域P2各指标在前2个主成分的载荷图Fig.4 Loading plot of six metrics in P2

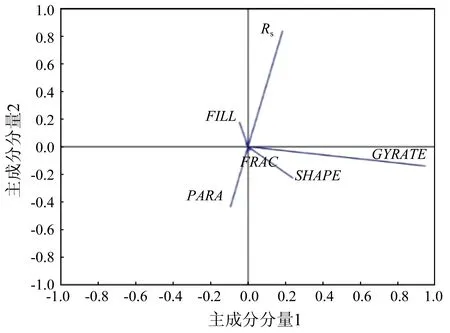
图5 实验区域P3各指标在前2个主成分的载荷图Fig.5 Loading plot of six metrics in P3

从图3可以看出，指标GYRATE在主成分分量1中的载荷系数超过0.90，紧随其后的是指标Rs，而其他指标的载荷系数都较小，指标GYRATE在主成分分量1中所占比例最大，故可将主成分分量1用指标GYRATE来表示。在主成分分量2中，指标Rs的载荷系数接近0.82，其他各指标的载荷系数都较小，指标Rs在主成分分量2中所占比重最大，故主成分分量2可用指标Rs来表示。同理，从图4和图5可以看出，在主成分分量1中，指标GYRATE的载荷系数均高达0.95，其他指标的载荷系数则较小，故主成分分量1可用指标GYRATE来表示。在主成分分量2中，指标Rs的系数分别接近0.90和0.85，Rs相对其他指标来说所占比重较大，故主成分分量2可用指标Rs来表示。由此可得，P1,P2和P3这3组斑块数据均可由GYRATE和Rs这2个指标来描述和表示。

2.3 实验验证

为验证斑块形态指标组合的有效性，本文基于3个实验区，对11个斑块形态指标进行两两组合，根据公式(3)计算其斑块识别度。由实验结果可知，采用双指标区分不同形态斑块时，3个实验区中，GYRATE和Rs组合对于不同形态斑块的识别程度都达到99%以上，这与2.2.3小节中分析结果保持一致。由此说明，GYRATE和Rs这个组合可以很好地描述和识别不同形态的斑块。

3 讨论与结论

本文选取11个斑块形态指标进行适用性描述及指标简化分析。通过对斑块指标定性描述及解释，明确了这些指标的适用范围及局限性。为了实现斑块形态指标的简化分析，实验采用GLC30数据，在四川省选取3个面积相同、形状一致，但景观格局不同的实验区域，基于实验区域栅格类别数据提取斑块，计算斑块级别指标值，并进行相关性和主成分分析，得到斑块形态指标简化结果，最后采用斑块识别度进行验证。由实验结果可知：

1)11个斑块形态指标可简化为2类指标，实现大部分不同形态斑块的描述和表达。

2)斑块形态可由回旋半径(GYRATE)和支撑半径(Rs)这2个指标来描述和表达。

本文选取主成分分析方法进行斑块形态指标分析，主成分分析方法对于样本数据具有一定的依赖性，当样本量足够大的时候，样本对于实验结果的影响可忽略不计。在以后的研究中，可尝试增加样本量进行分析，以进一步优化分析结果。

[1] 邬建国.景观生态学——格局、过程、尺度与等级[M].北京:高等教育出版社,2000.

Wu J G.Landscape Ecology:Pattern,Process,Scale and Hierarchy[M].Beijing:Higher Education Press,2000.

[2] 张秋菊,傅伯杰,陈利顶.关于景观格局演变研究的几个问题[J].地理科学,2003,23(3):264-270.

Zhang Q J,Fu B J,Chen L D.Several problems about landscape pattern change research[J].Scientia Geographica Sinica,2003,23(3):270-275.

[3] Cushman S A,McGarigal K,Neel M C.Parsimony in landscape metrics:Strength,universality,and consistency[J].Ecological Indicators,2008,8(5):691-703.

[4] 陈文波,肖笃宁,李秀珍.景观指数分类、应用及构建研究[J].应用生态学报,2002,13(1):121-125.

Chen W B,Xiao D N,Li X Z.Classification, application,and creation of landscape indices[J].Chinese Journal of Applied Ecology,2002,13(1):121-125.

[5] 龚建周,夏北成.景观格局指数间相关关系对植被覆盖度等级分类数的响应[J].生态学报,2007,27(10):4075-4085.

Gong J Z,Xia B C.Response to classification numbers of vegetation types on correlative coefficients among landscape metrics[J].Acta Ecologica Sinica,2007,27(10):4075-4085.

[6] 林孟龙,曹 宇,王 鑫.基于景观指数的景观格局分析方法的局限性:以台湾宜兰利泽简湿地为例[J].应用生态学报,2008,19(1):139-143.

Lin M L,Cao Y,Wang X.Limitations of landscape pattern analysis based on landscape indices:A case study of Lizejian wetland in Yilan of Taiwan Province,China[J].Chinese Journal of Applied Ecology,2008,19(1):139-143.

[7] 刘 宇,吕一河,傅伯杰.景观格局——土壤侵蚀研究中景观指数的意义解释及局限性[J].生态学报,2011,31(1):267-275.

Liu Y,Lyu Y H,Fu B J.Implication and limitation of landscape metrics in delineating relationship between landscape pattern and soil erosion[J].Acta Ecologica Sinica,2011,31(1):267-275.

[8] 刘小平,黎 夏,陈逸敏,等.景观扩张指数及其在城市扩展分析中的应用[J].地理学报,2009,64(12):1430-1438.

Liu X P,Li X,Chen Y M,et al.Landscape expansion index and its applications to quantitative analysis of urban expansion[J].Acta Geographica Sinica,2009,64(12):1430-1438.

[9] 张林艳,夏既胜,叶万辉.景观格局分析指数选取刍论[J].云南地理环境研究,2008,20(5):38-43.

Zhang L Y,Xia J S,Ye W H.Overview on choosing landscape indices in landscape pattern analysis[J].Yunnan Geographic Environment Research,2008,20(5):38-43.

[10] Riitters K H,O’Neill R V,Hunsaker C T,et al.A factor analysis of landscape pattern and structure metrics[J].Landscape Ecology,1995,10(1):23-39.

[11] 布仁仓,胡远满,常 禹,等.景观指数之间的相关分析[J].生态学报,2005,25(10):2764-2775.

Bu R C,Hu Y M,Chang Y,et al.A correlation analysis on landscape metrics[J].Acta Ecologica Sinica,2005,25(10):2764-2775.

[12] 彭保发,陈端吕,李文军,等.土地利用景观格局的稳定性研究——以常德市为例[J].地理科学,2013,33(12):1484-1488.

Peng B F,Chen D L,Li W J,et al.Stability of landscape pattern of land use:A case study of Changde[J].Scientia Geographica Sinica,2013,33(12):1484-1488.

[13] 彭 建,王仰麟,张 源,等.土地利用分类对景观格局指数的影响[J].地理学报,2006,61(2):157-168.

Peng J,Wang Y L,Zhang Y,et al.Research on the influence of land use classification on landscape metrics[J].Acta Geographica Sinica,2006,61(2):157-168.

[14] Lechner A M,Reinke K J,Wang Y,et al.Interactions between landcover pattern and geospatial processing methods:Effects on landscape metrics and classification accuracy[J].Ecological Complexity,2013,15:71-82.

[15] McGarigal K,Marks B J.FRAGSTATS:Spatial Analysis Program for Quantifying Landscape Structure[R].USDA Forest Service-General Technical Report PNW-GTR-351.Corvallis,OR,1995.

[16] EPA.Landscape Monitoring and Assessment Research Plan[R].EPA 620/R-94-009.Las Vegas,NV:Environmental Monitoring Systems Laboratory,1994.

[17] 陈 燕,齐清文,杨志平,等.数学形态学在黄土地貌单元分类学上的应用[J].山地学报,2005,23(1):96-100.

Chen Y,Qi Q W,Yang Z P,et al.Application of math-morphological features in relief taxonomy of Loess Plateau[J].Journal of Mountain Science,2005,23(1):96-100.

[18] 张春英,张春玲.植被景观指数随复合地形因子分异的变化规律[J].中国农学通报,2012,28(1):65-68.

Zhang C Y,Zhang C L.Law of landscape pattern indices responding to composite mountain factors spatial heterogeneity[J].Chinese Agricultural Science Bulletin,2012,28(1):65-68.

[19] 刘学录,董旺远,林慧龙.景观要素的形状指数与形状特征的关系[J].甘肃科学学报,2000,12(3):17-20.

Liu X L,Dong W Y,Lin H L.The relations between the shape index of the landscape elements and their shape features[J].Journal of Gansu Sciences,2000,12(3):17-20.

[20] 杨晓艳,闫东浩,程 锋.耕地整理的景观效应分析[J].自然资源学报,2005,20(4):572-581.

Yang X Y,Yan D H,Cheng F.Study on landscape effects from cultivated land consolidation[J].Journal of Natural Resources,2005,20(4):572-581.

[21] 毛 亮,李满春,刘永学,等.一种基于面积紧凑度的二维空间形状指数及其应用[J].地理与地理信息科学,2005,21(5):11-14.

Mao L,Li M C,Liu Y X,et al.A 2-dimensional shape index based on area compactness and its applications[J].Geography and Geo-Information Science,2005,21(5):11-14.

[22] 苏为华.多指标综合评价理论与方法问题研究[D].厦门:厦门大学,2000.

Su W H.Study on Comprehensive Evaluation Theory and Methodological Issues[D].Xiamen:Xiamen University,2000.

[23] Nankai S,Kawaguri M,Yoshioka T,et al.Quantitative analysis method and its system using a disposable sensor:U.S.,Patent 5266179[P].1993-11-30.

[24] 吴殿廷,吴 迪.用主成分分析法作多指标综合评价应该注意的问题[J].数学的实践与认识,2015,40(20):143-150.

Wu D T,Wu D.Some problems in comprehensive evaluation of the principal component analysis[J].Mathematics in Practice and Theory,2015,40(20):143-150.

[25] 陈述云,张崇甫.多指标综合评价方法及其优化选择研究[J].数理统计与管理,1994,13(3):18-21.

Chen S Y,Zhang C F.On methodology of multi-indicator composite evaluation[J].Application of Statistics and Management,1994,13(3):18-21.

ApplicabilityandsimplificationstudyofpatchlevellandscapemetricsbasedonGLC30

ZHANG Qianning1, TAN Shiteng1,2, XU Zhu1,2,3, HUANG Zechun1,2

(1.FacultyofGeosciencesandEnvironmentalEngineering,SouthwestJiaotongUniversity,Chengdu611756,China; 2.State-provinceJointEngineeringLaboratoryofSpatialInformationTechnologyforHigh-speedRailwaySafety,Chengdu610031,China; 3.CollaborativeInnovationCenterforRailTransportSafetyMinistryofEducationofthePeople’sRepulicofChina,Chengdu610031,China)

Patch is the basic unit in landscape pattern and patch metrics constitute an important basis for quantifying patch morphology. Presently there are many patch level metrics and most of them have certain redundancy. Therefore for the purpose of applying patch metrics reasonably, the objectives of this paper are the applicability analysis of patch morphological metrics, the multiple-index analysis based on the patch morphological metrics and reducing many patch metrics to several patch metrics to express different patches. by the correlation analysis and principal component analysis. The experiment is on the basis of applicability analysis about 11 patch morphological metrics with global land cover data (GLC30), and all the metrics except area and perimeter are simplified by the two analysis methods. The experiment result shows that the two patch metrics, radius of gyration and support radius, could express and describe the different morphological patches well. The experimental results could serve as an important reference for the quantitative study of the scale effect in the landscape pattern.

GLC30； landscape pattern metrics; patch; principal component analysis; correlation analysis

10.6046/gtzyyg.2017.04.15

张倩宁，谭诗腾，徐柱，等.基于GLC30数据的斑块级别景观指标适用性及简化研究[J].国土资源遥感,2017,29(4):98-105.(Zhang Q N,Tan S T,Xu Z,et al.Applicability and simplification study of patch level landscape metrics based on GLC30[J].Remote Sensing for Land and Resources,2017,29(4):98-105.)

TP 79

A

1001-070X(2017)04-0098-08

2016-05-18；

2016-07-25

测绘地理信息公益性行业科研专项项目“全球地表覆盖数据分析”(编号： 201512028)、教育部创新团队资助项目“高速铁路运营安全空间信息技术”(编号： IRT13092)和中央高校基本科研业务费专项资金项目“基于地统计模型的LiDAR点云数据生成DEM的精度分析”(编号： 2682014CX017)共同资助。

张倩宁(1992-)，女，博士研究生，主要研究方向为GIS时空数据多尺度建模与分析。Email: zhangqianning1020@163.com。

(责任编辑：张仙)