一种混沌萤火虫算法的WSN节点分布优化研究
董晓丹, 丁 力
(1.江苏信息职业技术学院,江苏 无锡 214153; 2. 南京航空航天大学,南京 210016)
一种混沌萤火虫算法的WSN节点分布优化研究
董晓丹1, 丁 力2
(1.江苏信息职业技术学院,江苏 无锡 214153; 2. 南京航空航天大学,南京 210016)
针对无线传感器网络节点分布优化问题,提出了一种有效的混沌萤火虫优化算法。在保证节点相互连通的前提下,建立了无线传感器网络对目标区域覆盖的数学模型,并将节点分布优化问题转换为求解函数最大值问题;利用萤火虫算法优越的寻优能力来实现最优的网络节点分布,并引入立方映射混沌算子来提高算法的局部搜索能力和保持种群的多样性。通过标准函数测试与无线网络覆盖优化仿真对所提算法进行了验证,结果表明:与其他算法相比,所提算法能够较好地跳出局部最优的束缚,具有优化效果佳、稳定性好、鲁棒性强的优点,能够满足无线传感器网络节点分布优化的要求。
无线传感器网络; 节点分布; 萤火虫算法; 混沌算子
0 引言
无线传感器网络(Wireless Sensor Networks,WSN)是由多个移动或静止的传感器节点以自组织形式构成的多跳无线网络。它能够在恶劣或特殊环境下感知、采集、处理与传输网络覆盖区域内被监测对象的信息,在军用与民用上有着广泛的应用前景,近年来一直是国内外研究的热点[1-2]。合理布置网络节点有助于提高WSN的工作效率,减少能量耗散。因此,研究如何对网络节点进行分布优化已成为WSN关键性技术之一。
针对WSN节点分布优化问题,国内外很多学者采用人工智能算法来进行处理。例如,文献[3]利用粒子群算法(Particle Swarm Optimization Algorithm,PSO)有效处理了WSN节点分布优化问题,但PSO算法迭代效率低、定向性差且易陷入局部最优值;在保证网络连通性的前提下;文献[4]通过遗传算法(Genetic Algorithm,GA)的优化机制,得到WSN区域覆盖所需的最优节点集,但仍未解决算法前期收敛过早、后期收敛速度变慢的问题。近期研究成果表明,利用改进算法进行优化计算更具优势,也是学者们研究的重点。文献[5]将差分进化算法(Different Evolution Algorihtm,DE)与人工蜂群算法(Artificial Bee Colony Algorithm,ABC)结合,提出了一种DABC算法来解决WSN节点分布优化问题;文献[6]采用数据聚合算子来改进蚁群算法(Ant Colony Algorithm,ACO),并极大化WSN有效覆盖面积的问题,提出了一种基于DAACO算法的WSN节点分布优化机制。
萤火虫算法是由KRISHNANAND[7]提出的一种新兴元启发式优化算法,已被成功应用于WSN节点分布优化。但是,和其他全局算法一样,基本的萤火虫算法也易于陷入局部最优值导致出现早熟和种群多样性降低的问题。本文利用立方映射混沌算子来改进传统的萤火虫算法,提出了一种混沌萤火虫算法(Chaotic Glowworm Swarm Optimization,CGSO)来解决WSN节点分布优化问题,该算法在萤火虫位置初始化过程中使用混沌序列,有效保证了种群的多样性而且避免了算法的早熟现象,同时,也给出了以网络覆盖率为目标函数的描述。最后,通过标准函数测试与WSN仿真算例对本文所提算法的性能进行了验证与分析。
1 问题描述
假定将一个二维平面区域A离散化为s×s的网格,每个网格的面积为1。整个区域内分布着n个无线传感器节点,每个节点都可通过某些特殊的方式或GPS来获取自身位置,并具有相同的感知半径R。因此,区域A上的所有WSN节点集可表示为
S={s1,s2,…,sn}
(1)
式中,si=(xi,yi),i=1,2,…,n,(xi,yi)为节点si在区域A内的坐标。对于任意网格点pj,j=1,2,…,m×n,其与节点si的距离为
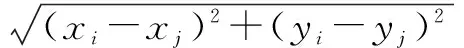
(2)
另外,本文采用文献[8]提出的概率测量模型来计算WSN的覆盖率。节点si对网格点pj的检测概率Cij可描述为
(3)
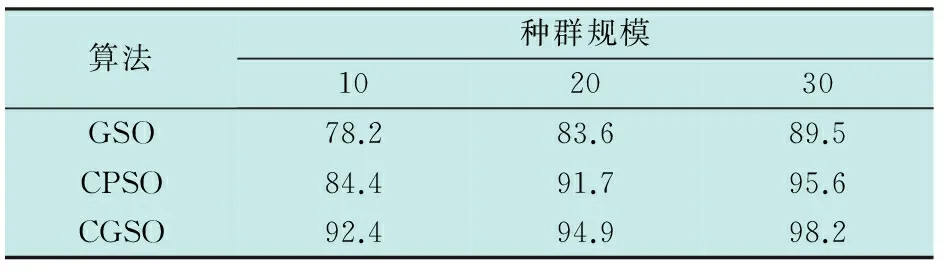
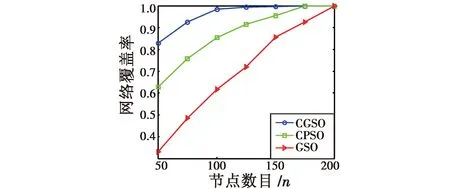
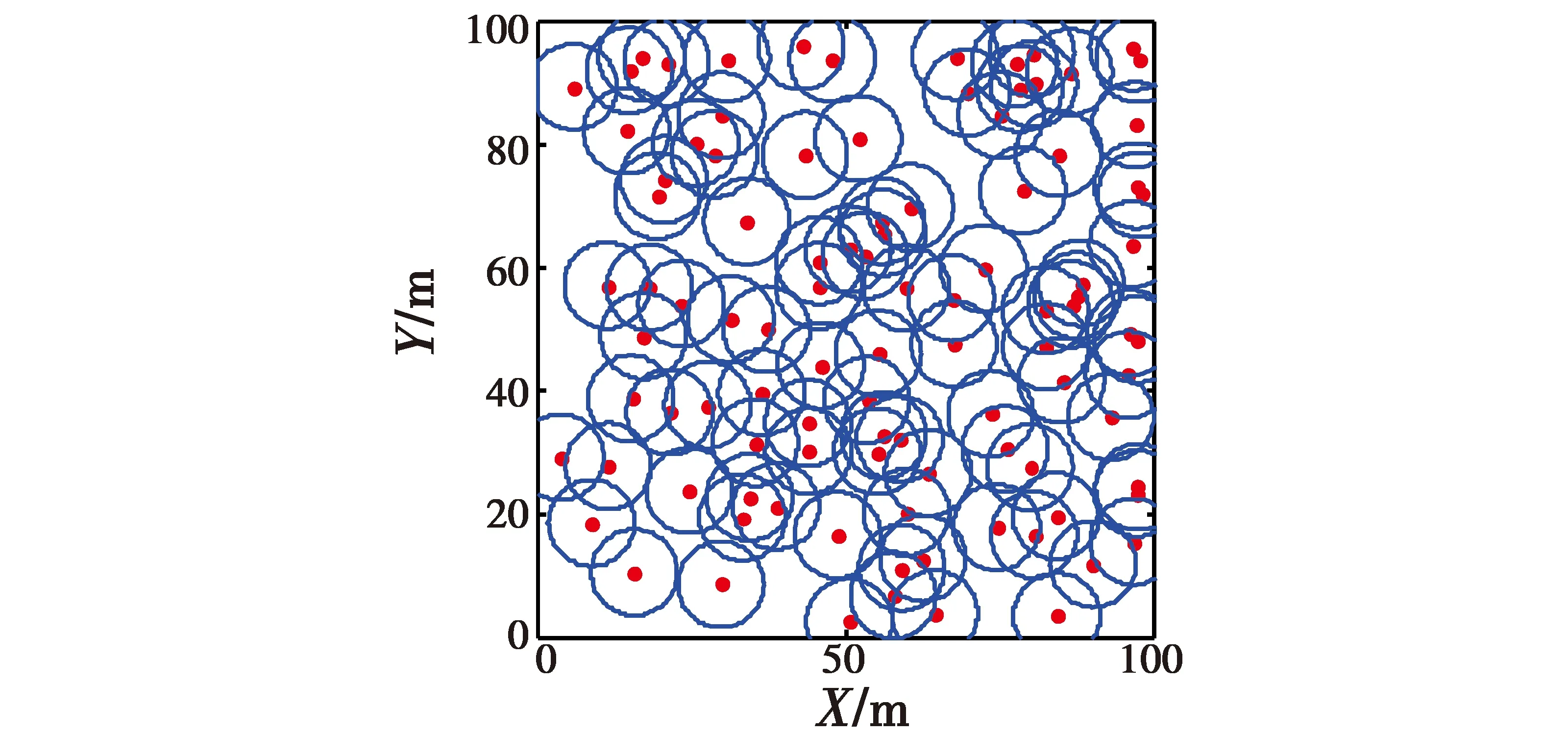
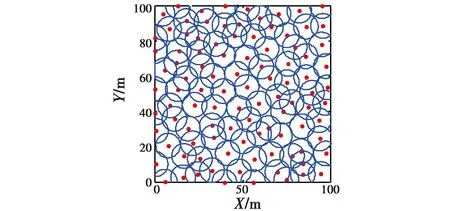
式中:Re(0 假定所有节点检测都是相互独立事件,那么由点pj被单个节点检测的概率可得其被所有节点同时检测到的综合概率为 (4) 式中:若Cj小于某个特定阈值Ct,则认为点pj不被检测;反之,若Cj大于或等于某个特定阈值Ct,则认为点pj被节点检测。本文取Ct=0.75。 然后,通过点pj被检测的综合概率来衡量每个网格的覆盖率,即根据式(4)计算每个网格点的检测概率,将被检测网格点的个数占网格总数的比例作为WSN的覆盖率。具体的数学描述为 (5) 因此,WSN节点分布优化问题可描述为目标区域A上的n个无线传感器节点通过优化算法达到对整个目标区域的覆盖。也就是,该问题可转换为式(5)的最大化问题,即 (6) GSO算法是对萤火虫之间互相吸引和位置更新的模拟。算法主要由4个部分构成,即初始化萤火虫、荧光素更新、位置更新和决策域更新[9]。在算法中,定义t时刻第i只萤火虫的位置和该处的荧光素值分别为xi(t),li(t),并且每个位置对应的一个目标函数值f(xi(t)),也就是WSN区域覆盖率。 算法初始时,萤火虫i的位置随机产生,即 xi(t)=L+rand(0,1)·(U-L)i=1,…,M (7) 式中:M为萤火虫种群总数;L和U分别是xij取值的下限和上限。 当每只萤火虫在其区域决策范围内向其邻域个体传递信息时,决策范围更新为 (8) 萤火虫i决策范围内的个体数量为 (9) 式中,xj(t)和lj(t)分别为萤火虫j的位置与荧光素值。 萤火虫i的运动方向由其邻域内各萤火虫的荧光素数量来决定,而萤火虫i向其邻域内萤火虫j移动的概率为 (10) 移动后,萤火虫i的新位置为 (11) 式中,s为移动步长。 荧光素值的大小由目标函数值f(xi(t))决定,当萤火虫i更新位置后,新的荧光素值重新计算为 li(t)=(1-ρ)li(t-1)+γf(xi(t)) (12) 式中:ρ∈(0,1)为常数,与荧光素挥发有关;γ为荧光素更新率。 在邻域集合中,当萤火虫i找到具有更高荧光素值的萤火虫j时,如果这两个体间的距离小于感知半径,则萤火虫i以概率Pij(t)选择萤火虫j,并向该方向移动;然后按式(11)更新位置,并计算新位置的目标函数值;最后,按式(12)对荧光素值进行更新;直至算法迭代次数达到Tmax,输出最优解。 为了克服GSO算法易陷入局部最优值和全局开采能力不足的缺点,本文利用混沌算子遍历性、规律性与随机性的特点进行优化搜索,并保持种群的多样性。混沌算子的形式有很多种,不同的混沌算子对混沌优化过程的影响不同。目前引用较多的是Logistic混沌算子,但算法的寻优速度易受Logistic遍历不均匀的影响而导致迭代效率降低。文献[10]通过严格的数学推理证明了立方混沌映射要比Logistic映射具有更快的收敛速度与更好的遍历均匀性,故本文采用立方混沌算子来改进GSO算法的位置初始化。产生混沌序列为 y(n+1)=4y(n)3-3y(n)n=0,1,…,M (13) 式中,y(n)∈[-1,1]。 将混沌序列映射到待优化变量的取值空间内,并实现对萤火虫初始位置的混沌搜索。详细步骤如下。 1) 对于D维空间内的M个个体,随机产生一个D维向量Y=(y1,…,yd)作为新个体,其中,yi∈[-1,1],1≤i≤d。 2) 利用式(13)对Y逐维进行M-1次迭代,这就产生了其余M-1个个体。 3) 将产生的混沌变量映射到解的搜索空间内,即 (14) 式中:xid为萤火虫i在第d维的位置;yid为利用式(13)产生的萤火虫i的第d维值。 根据分析可知,GSO算法的时间复杂度为O(M×Tmax)。由于增加了混沌搜索算子,CGSO算法的时间复杂度取决于混沌序列的长度K,故混沌搜索阶段的时间复杂度为O(K×Tmax)。但根据参数敏感性分析[11],种群大小M与混沌序列K呈线性关系,经过约减后CGSO算法的时间复杂度也为O(M×Tmax)。因此,两种算法的时间复杂度是相同的。 为了测试CGSO算法的性能,本文采用文献[12]提出的4个标准测试函数进行测试,并与CPSO算法、GSO算法比较。4个函数的理论全局最小值均为0,为了公平比较各算法的优化性能,设置各算法的种群规模为20,各测试函数的维数为30,迭代次数为1000次。然后,通过各算法分别对各测试函数进行50次独立测试,表1给出了测试的统计结果,包括平均值(Mean)和标准差(SD)。 表1 函数优化的结果 由表1可知,CGSO算法在Sphere,Rastrigin和Griewank函数上,无论是平均值还是标准差均优于GSO算法与CPSO算法,而且都有明显的数量级提升。虽然,CGSO算法在Ackley函数上性能要略低于CPSO算法,但它们的平均值和标准差仍处于同一数量级。这说明与其他两种算法相比,CGSO算法具有更强的寻优能力和更高的求解质量。 为了验证本文所提算法在处理WSN节点分布优化问题的有效性,假设WSN的监控范围为100 m×100 m的正方形区域,传感器节点的感知半径R为7 m。在监控范围内随机分布着100个WSN节点,通过GSO算法、CPSO算法和CGSO算法分别对其进行优化处理,各迭代1000代,重复操作50次,记录下其中的最优解。 3种算法的参数设置如下:在GSO算法和CGSO算法中,M=20,ρ=0.4,γ=0.6,β=0.1,nt=8,s=0.03;在CPSO算法中,种群大小为20,学习因子c1=c2=2,权重因子W=0.8[13]。 当算法运行结束后,统计各算法的最优覆盖率与平均覆盖率,相应结果如表2所示。从表中可以看出,经混沌算子改进后的GSO算法优化成功率得到了大大的提升。 表2 3种算法结果对比 图1给出了3种算法网络覆盖率最优解的迭代曲线。从图中可见,GSO算法与CPSO算法分别到了411次和197次迭代才开始收敛,而CGSO算法到了156次迭代便开始收敛。另外,本文算法获得的最优网络覆盖率为99.44%,而CPSO算法与GSO算法获得的分别为98.87%和98.13%。这表明CGSO算法收敛速度快,全局搜索能力强,能够摆脱局部最优的束缚。 图1 3种算法网络覆盖率最优解的迭代曲线Fig.1 Optimal iteration curves of three algorithms 另外,为了验证种群规模对算法性能的影响,设置种群大小分别为10, 20和30,运行500代。通过3种算法获得的网络覆盖率如表3所示。从表中可以看出,随着种群规模的扩大,CGSO算法的寻优精度要高于其他算法,这表明本文所提算法能够获取更多的搜索信息和保持种群的多样性。 表3 不同种群规模下各算法的优化结果比较 为了进一步验证CGSO算法的性能,设计了基于不同节点数目的网络覆盖率仿真。3种算法的网络覆盖率随节点密度的变化曲线如图2所示。从图中可以看出,要实现90%以上的覆盖率,GSO算法与CPSO算法各需要布置125和175个节点,而CGSO算法只需要布置75个节点,这说明CGSO算法对全局信息的开采速度快。 图2 网络覆盖率比较图Fig.2 Network coverage when node density changes 从图3与图4可以看出,初始状态杂乱无章的节点经CGSO算法优化布置后,分布比较均匀,重叠覆盖率相对较小。因此,本文提出的基于CGSO算法的WSN节点分布优化策略可以合理解决网络覆盖优化问题,并能有效提高网络覆盖率。 图3 初始节点分布图Fig.3 Initial node distribution 图4 经CGSO算法优化后的节点分布图Fig.4 Node distribution based on CGSO 本文针对无线传感器网络节点分布优化问题,提出了一种基于混沌萤火虫算法(CGSO)的节点分布优化方案。该算法利用立方映射混沌算子改进了GSO算法中萤火虫初始位置的更新策略,保持了种群的多样性,提高了算法的收敛速度与全局搜索能力。 与GSO算法和CPSO算法相比,CGSO算法在求解标准测试函数上有更高的求解质量与更快的收敛速度。 在优化WSN节点分布算例中,CGSO算法的最优网络覆盖率比CPSO算法和GSO算法分别提高了0.57%和1.31%。在获得同样网络覆盖率的条件下,CGSO算法所需的节点数量更少。 [1] ANTONIO P,GRIMACCIA F,MUSSETTA M.Architecture and methods for innovative heterogeneous wireless sensor network applications[J].Remote Sensing,2012,4(5):1146-1161. [2] ZHANG J,ZHANG M.Energy efficient dynamic mixed key management scheme based on virtual grid in wireless sensor netwoks[J].Journal of Convergence Information Technology,2011,6(7):111-118. [3] KUILA P,JANA P K.Energy efficient clustering and routing algorithms for wireless sensor networks:particle swarm optimization approach[J].Engineering Applications of Artificial Intelligence,2014(33):127-140. [4] HUSSAIN S,MATIN A W,ISLAM O.Genetic algorithm for hierarchical wireless sensor networks[J].Journal of Networks,2007,2(5):87-97. [5] 熊伟丽,刘欣,陈敏芳,等.基于差分蜂群算法的无线传感器网络节点分布优化[J].控制工程,2014,6(21):1036-1040. [6] LIN C,WU G,XIA F,et al.Energy efficient ant colony algorithms for data aggregation in wireless sensor networks[J].Journal of Computer and System Sciences,2012,78(6):1686-1702. [7] KRISHNANAND K N,GHOSE D.Glowworm swarm optimisation: a new method for optimising multi-modal functions[J].International Journal of Computational Intelligence Studies,2009,1(1):93-119. [8] ÖZTÜRK C,KARABOA D,GÖRKEMLB.Artificial bee colony algorithm for dynamic deployment of wireless sensor networks[J].Turkish Journal of Electrical Engineering & Computer Sciences,2012,20(2):255-262. [9] KRISHNANAND K N,GHOSE D.A glowworm swarm optimization based multi-robot system for signal source localization[M].Berlin:Springer Heidelberg,2009:49-68. [10] CHEN G,WU X D,ZHU X Q,et al.Efficient string mat-ching with wildcards and length constraints[J].Knowledge and Information Systems,2006,10(4):399-419. [11] 王翔,李志勇,许国艺,等.基于混沌局部搜索算子的人工蜂群算法[J].计算机应用,2012,32(4):1033-1036. [12] LEI L,SHIRU Q.Path planning for unmanned air vehicles using an improved artificial bee colony algorithm[C]//31st Chinese Control Conference (CCC),IEEE, 2012: 2486-2491. [13] 陈志敏,薄煜明,吴盘龙,等.混沌粒子群优化粒子滤波算法[J].电光与控制,2013,20(1):36-40. ChaoticGlowwormSwarmOptimizationAlgorithminSensorDeploymentforWirelessSensorNetworks DONG Xiao-dan1, DING Li2 (1.Jiangsu Vocational College of Information Technology,Wuxi 214153,China;2.Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China) Aiming at node deployment optimization in wireless sensor networks,an effective chaotic glowworm swarm optimization was proposed.On the premise that connectivity among nodes was guaranteed,we established a mathematical model to achieve the coverage of objective area with wireless sensor networks,and transformed the node-deployment optimization problem into finding the largest value of a function.The glowworm swarm optimization with the strong search performance was used to search the optimal node deployment.And the cubic mapping chaotic operator was introduced to enhance the ability of local search and robustness and to keep the diversity of population.Then,the proposed algorithm was verified through the numerical benchmark functions and coverage simulation.All the results showed that the proposed algorithm has the ability to jump out of local optimum and has good optimization results,nice stability and strong robustness.Hence,it can satisfy the requirement of optimal node deployment in wireless sensor networks. wireless sensor network; node deployment; glowworm swarm optimization; chaotic operator TP18 A 1671-637X(2017)03-0073-04 2016-05-05 2016-06-03 江苏省高校品牌专业建设工程资助项目 (PPZY2015B190) 董晓丹(1981 —),男,江苏无锡人,硕士,讲师,研究方向为通信技术、智能算法等。
2 混沌萤火虫算法
2.1 基本算法
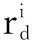
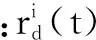
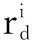
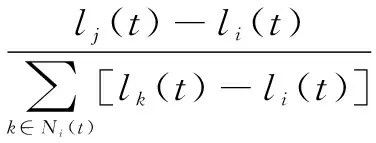
2.2 立方映射混沌算子
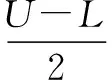
2.3 算法的时间复杂度分析
3 仿真分析
3.1 标准函数测试

3.2 WSN仿真实例


4 结束语

