大气传输及目标反射对圆偏振光特性影响研究
赵帧娜, 羊 毅, 王建洲, 滕云鹏, 李成杰, 沈兆国, 孙 军
(1.光电控制技术重点实验室,河南 洛阳 471000;2.中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000;3.西安重装渭南光电科技有限公司,陕西 渭南 714000; 4.南开大学物理科学学院,天津 300071)
大气传输及目标反射对圆偏振光特性影响研究
赵帧娜1,2, 羊 毅2, 王建洲3, 滕云鹏2, 李成杰2, 沈兆国2, 孙 军4
(1.光电控制技术重点实验室,河南 洛阳 471000;2.中国航空工业集团公司洛阳电光设备研究所,河南 洛阳 471000;3.西安重装渭南光电科技有限公司,陕西 渭南 714000; 4.南开大学物理科学学院,天津 300071)
主要对大气传输及目标反射对偏振光的特性影响进行研究,以蒙特卡罗方法为基础,采用斯托克斯-穆勒形式,依据Mie散射理论及偏振双向反射函数模型,追踪每个光子的偏振态变化,最后统计分析变化后偏振光的斯托克斯矢量和偏振信息。依据所建立的模型进行仿真,仿真结果表明,当能见度为23 km,距离为100 km,目标折射率为1.44+5.23i,表面粗糙度为0.1 mm时,大气传输对光偏振特性影响较小,而目标反射的影响较大,在接收端圆偏振光退偏为椭圆偏振光。
激光测距; 偏振特性; 大气传输; 目标反射; 斯托克斯矢量
0 引言
在机载激光测距系统中,小型载荷能够为系统提供更大的可用空间,而且风险相对较小、成本较低。利用光的偏振特性对激光测距机的光学接收和发射天线进行合置,可以减小光学天线的体积及重量,实现测距机系统的小型化。由于远程测距过程中光的偏振特性会发生变化,进而影响测距机性能,所以有必要对偏振辐射大气传输及典型目标的偏振特性进行研究。本文在前人单独研究大气、目标对光偏振特性影响的基础上[1-3],综合研究了二者对光偏振特性的影响。本文利用Monte Carlo方法仿真分析圆偏振光的偏振变化特性,研究结果不仅可为激光测距提供理论依据,同时可为日趋成熟的偏振探测成像、激光偏振通信等研究提供参考。
1 基本概念及模型理论
1.1 偏振光的Stokes矢量表示
Stokes矢量是用于描述光偏振状态的四元素向量[4],可用于表示自然光、完全偏振光及部分偏振光。对于完全偏振光可表示为

(1)
式中:I为光强度;χ为全偏振光的椭圆率角(表征椭圆率及旋转方向);ψ为全偏振光的方向角(表征偏振光偏振方向)。一些常见偏振光的Stokes参量如表1所示。
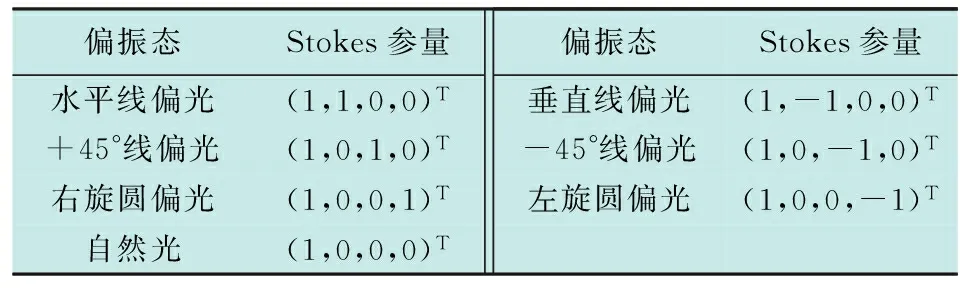
表1 常见偏振光的Stokes参量
邦加(Poincare)球是基于Stokes矢量的一种偏振态表示方法。如图1所示,将偏振态表示在坐标为(Q,U,V),半径为I的球面上。
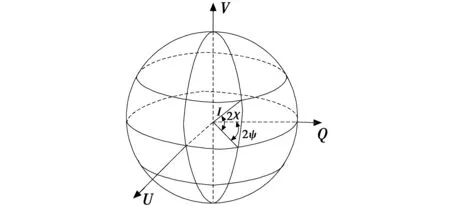
图1 邦加球Fig.1 Poincare globe
1.2 Mie散射理论
假设大气中的粒子为均匀各向同性的球形粒子,当沿Z轴传播的光子与单个球形粒子发生散射时,如图2所示。
设垂直和平行于散射面的电场分量分别为E⊥和E‖,如果发射光为椭圆偏振光,那么入射光的垂直分量仅产生散射光的垂直分量,入射光的水平分量也仅产生散射光的水平分量,则散射场可以表示为[5]
(2)
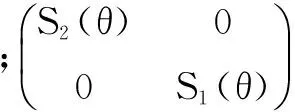
(3)
式中:an,bn为Mie散射系数;πn,τn为递推函数。其表达式为
(4)
式中:θ为散射角;x为散射球形粒子尺寸;m是粒子复折射率;ψn,ξn分别是贝塞尔函数和第一类汉克尔函数。

图2 入射光子与大气粒子散射示意图Fig.2 Definition of the geometry used to describe the scattering event of an incident photon by an atmospheric particle
设入射光Stokes矢量为Si,散射光Stokes矢量为Sr,则有
Sr=M(θ)Si
(5)
式中,M(θ)为根据Mie散射理论决定的单次散射Mueller矩阵,对于各向同性的球形粒子,其形式如式(6)所示,各元素数值如式(7)所示,S*为S的共轭。
(6)
(7)
由以上理论得,确定了粒子尺寸及散射角即可得到变化后偏振光的Stokes矢量。
1.3 偏振双向反射分布函数
偏振双向反射分布函数(pBRDF)是对表面反射偏振特性研究的典型模型之一[6],是由表面粗糙度参量、光学常数参量、方位角和散射角等多因素共同决定。图3为光子在目标表面发生反射的示意图。一般认为偏振双向反射分布函数包括偏振的镜面反射和非偏振的漫反射这两部分,其中,漫反射表示入射辐射经微面元多次反射,并认为其不具有偏振特性,所以忽略微面元间多次散射[7],Priest-Germer给出了pBRDF反射的一般表达式[8]为

M(θi,θr,φ)
(8)
式中:σ是表面粗糙度;α是微面元法线与粗糙面法线
之间的夹角;θi,θr是入射角及散射角;φ是散射方位角与入射方位角的差值φ=φr-φi。
M(θi,θr,φ)具体表达式需要由菲涅耳反射理论并考虑微面元坐标与目标表面坐标之间的转换推导得到。用琼斯矩阵T来表示入射和反射辐射s,p振动分量电场矢量的传输关系为[9-10]
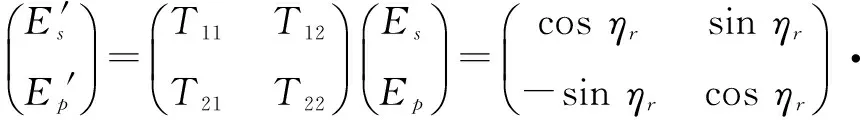
(9)
式中:rs,rp为菲涅尔反射系数;ηi,ηr分别表示入射和散射方向与目标表面法线和微面元法线组成的平面的夹角。
由琼斯矩阵T与穆勒矩阵M之间的转换关系,可得到M各元素的表达式[10],即
(10)
利用式(8)和式(10)得到偏振双向反射分布函数4×4矩阵形式,从而可以得到入射和反射Stokes矢量之间的传递关系S′=f(θi,θr,φ)S。

图3 目标表面反射示意图Fig.3 Sketch of target surface reflection
1.4 Monte Carlo方法
Monte Carlo方法不涉及求解辐射传输方程,是一种随机模拟方法,直接模拟辐射传输过程,即追踪每一个光子在传输过程中的行迹。它将大气散射过程当成是光子与大气中的粒子碰撞过程,将目标反射当成是光子与目标微面元碰撞过程。光子在大气中两次碰撞之间所走的距离与大气衰减系数有关,碰撞后光子将改变前进方向,散射角由相函数确定,碰撞后光子的Stokes矢量依据Mie散射理论得到,光子到达目标后根据pBRDF得到经目标反射后的Stokes矢量,再经由大气传输到达接收系统,最后对大量的光子“行为”跟踪并进行统计就可得到接收端偏振光的斯托克斯矢量和偏振信息。图4为Monte Carlo 方法流程图。

图4 Monte Carlo 方法流程图Fig.4 Flow chart of Monte Carlo method
2 仿真实验
仿真实验中,采用激光器波长为1.064 μm,发散角为0.2 mrad,出射光先经过水平线偏器,再经过快轴与水平夹角为45°的1/4波片,变为右旋圆偏振光,经过大气传输及目标反射回到接收面,如图5所示。初始Stokes矢量为(1,0,0,1)T,椭圆率角χ=45°,方向角ψ=0°。光子数为1 000 000,目标距离为100 km,高度为5 km,能见度为23 km,大气衰减系数为2.6×10-3/km[11]。

图5 光子传输示意图Fig.5 Sketch of photons transmission
依据上文中的模型,再确定了粒子尺寸、散射角目标表面粗糙度参量、光学常数参量就可以得到变化后偏振光的Stokes矢量。
2.1 粒子尺寸的选取
利用文献[12]中某地区(乡村型)的气溶胶谱分布模型,该模型使用4个对数正态分布的叠加来描述整个气溶胶尺寸谱分布, 即
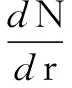
(11)
式中参数如表2所示[12],根据谱分布确定粒子半径。

表2 4个对数正态分布的参数
2.2 散射角的确定
采用经常使用的H-G函数(式12)近似表示散射相函数,即

(12)
式中,g为非对称因子。
由H-G函数可确定散射角θ的抽样函数为
(13)
式中,ξ为(0,1)上均匀分布的随机数,表示散射角取(0,θ)间的概率。
2.3 典型目标的选取
在机载应用场合,目标一般为高速运动、体积较小的飞行器,所以选铝合金为典型目标材质,折射率在波长1.064 μm处为1.44+5.23i,表面粗糙度为0.1 mm。
3 结果与分析
光子首先经大气传输到达目标后,偏振态如图6a所示;再经目标反射后,偏振态如图6b所示;最后到达接收面,偏振态如图6c所示。用邦加球表示各阶段光子的偏振态。

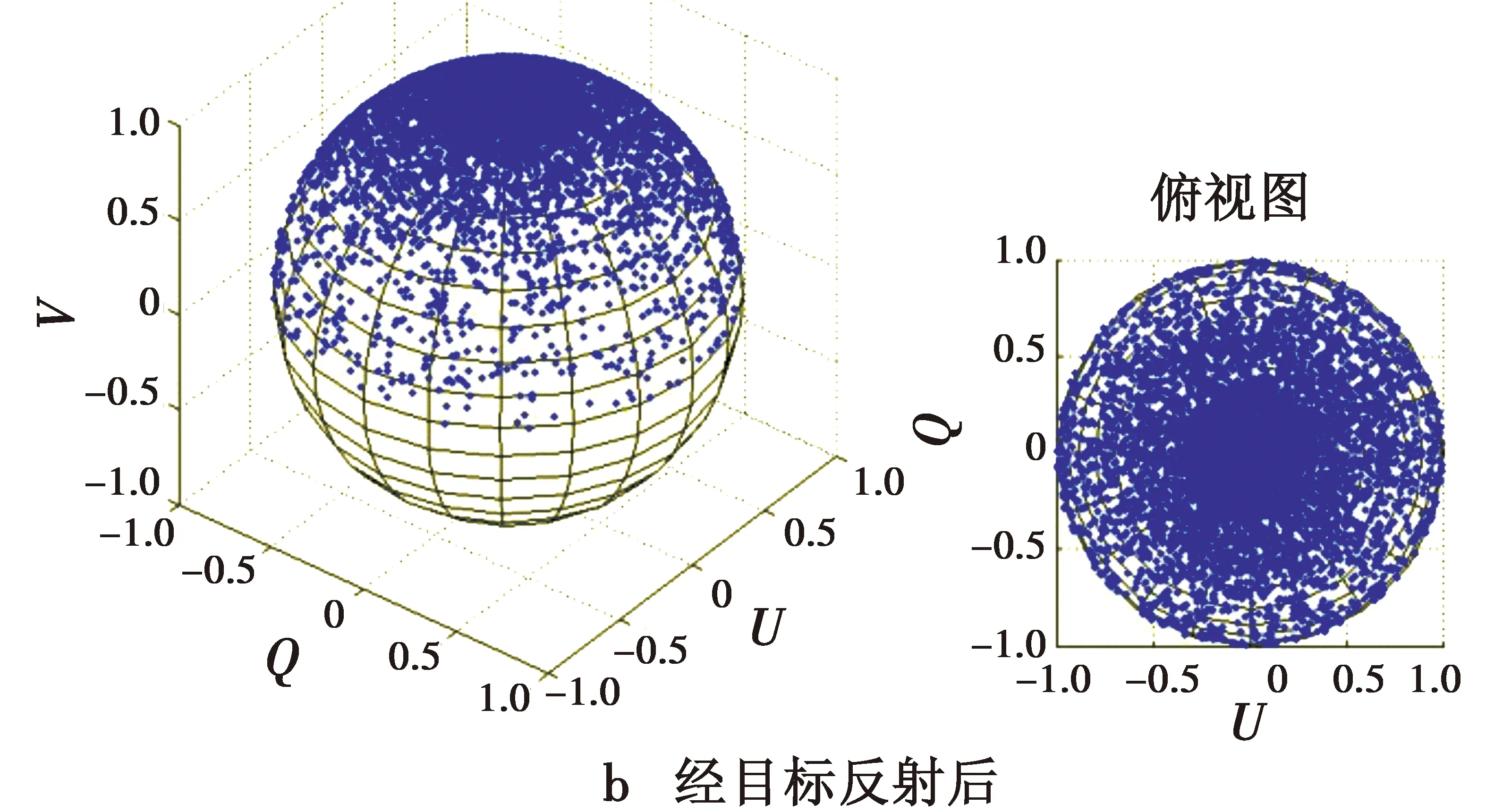

图6 光子Stokes矢量分布图Fig.6 Stokes vector distribution of photons
由图可以看出,图6a与原右旋圆偏振光所处的北极点相比较,变化不大,图6b较图6a变化程度大,图6c较图6b变化程度小,说明大气传输对光的偏振性改变不大,光子保偏性较好,目标对偏振特性影响较大,是决定性因素。
对仿真数据进行统计及归一化处理,则到达目标处、经目标反射后及接收面光子的方向角ψ和椭圆率角χ的分布图,如图7所示。
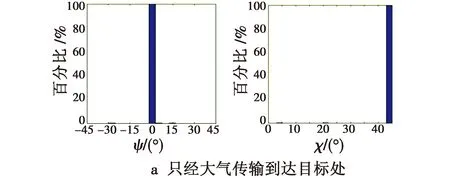
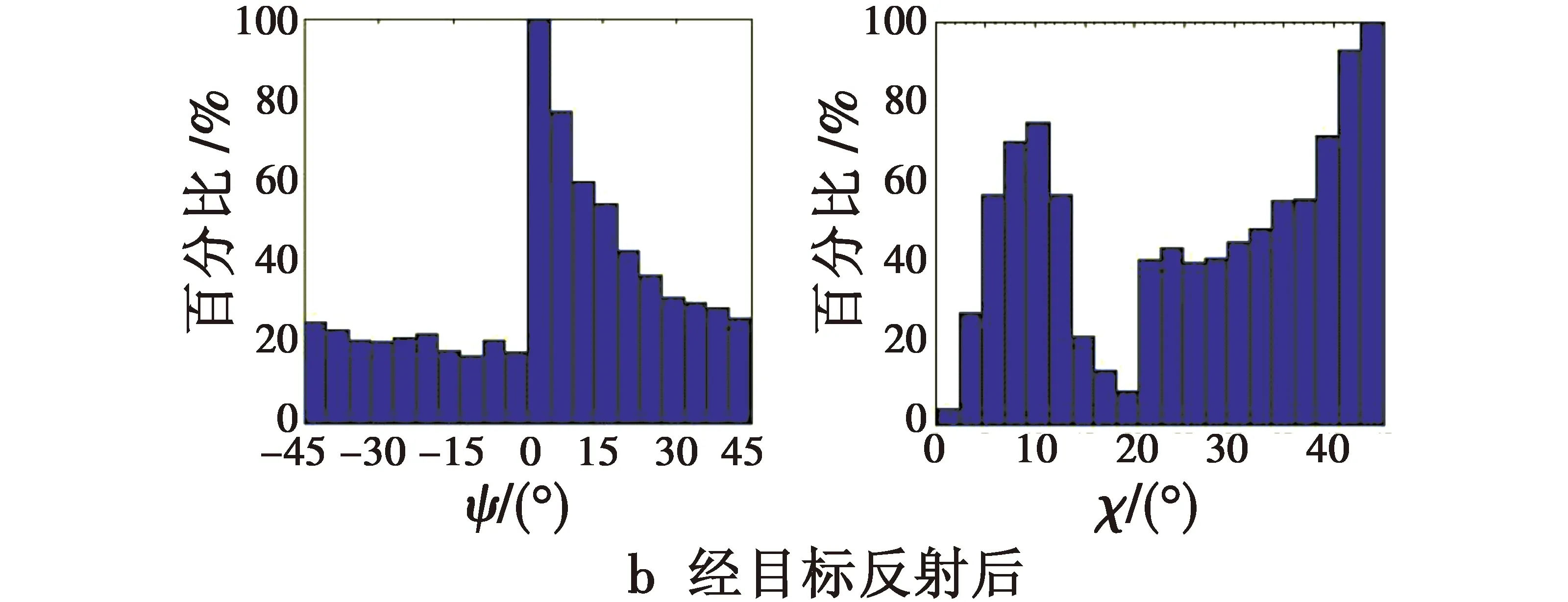
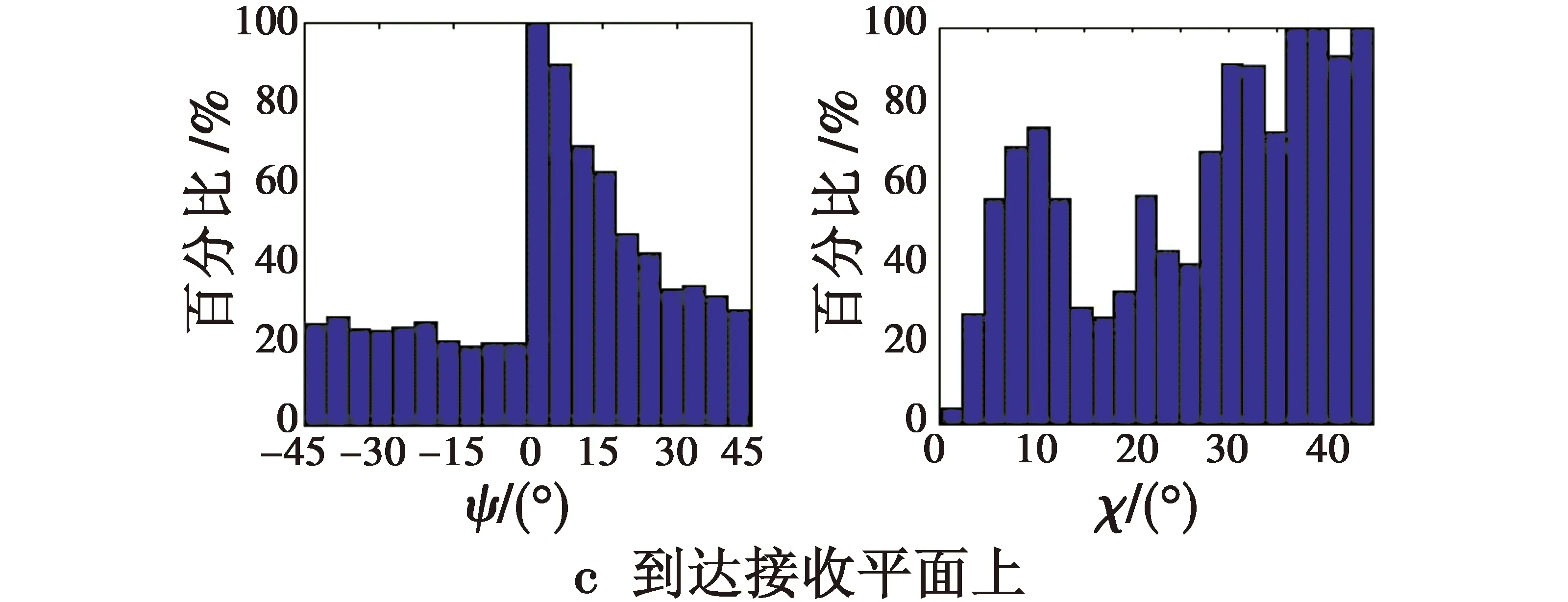
图7 光子ψ,χ角分布Fig.7 ψ and χ angular distribution of photons
对比图7中6个图可知,只经过大气传输,光子的保偏性能较好,通过统计计算,有0.99的概率方向角ψ的改变量不超过1°,有0.99的概率椭圆率角χ改变量不超过1°。说明在给定的大气环境下,大气传输对光偏振态影响较小;经目标反射后,光子的保偏性能较差,且随机性比较大,有0.322的概率方向角ψ的改变量不超过5°,有0.386的概率椭圆率角χ的改变量不超过5°,说明相对于大气传输,目标反射对光偏振态影响很大;到达接收面,有0.277概率方向角ψ的改变量不超过5°,有0.354的概率椭圆率角χ的改变量不超过5°。
为量化圆偏振光的退偏情况,在接收端加上快轴与水平夹角为45°的1/4波片,对光子通过1/4波片后的偏振态与原来的右旋偏振光进行对比。令t为光子垂直分量光强占总光强比例(右旋圆偏光经过该波片后,变为垂直线偏光,即t值为1)。对光子偏振态进行统计及归一化后,t值分布图如图8所示,进行统计计算后有57.88%的光子大于0.7,间接表明光的退偏程度。

图8 光子t值分布Fig.8 t values distribution of photons
4 结束语
本文建立了一种综合研究大气传输及目标反射对光偏振特性影响的模型,并应用模型针对典型大气环境及典型目标进行仿真,对各个阶段光子偏振态进行统计,结果表明,大气传输对光偏振特性影响较小,而目标反射的影响较大,在接收端圆偏振光退偏为椭圆偏振光,退偏程度与大气粒子及目标特性等有关。研究模型及结果不仅可为激光偏振测距提供理论依据,也为偏振成像等研究提供理论借鉴。
[1] CORNET C,C-LABONNOTE L,SZCZAP F.Three-dimensional polarized Monte Carlo atmospheric radiative transfer model (3DMCPOL):3D effects on polarized visible reflectances of a cirrus cloud[J].Journal of Quantitative Spectroscopy and Radiative Transfer,2010,111(1):174-186.
[2] 胡来归,向洲鹏,隋成华,等.蒙特卡罗方法对偏振光在大气中传输特性的研究[J].浙江工业大学学报,2015,43(4):416-419.
[3] 高明,宋冲,巩蕾.基于偏振双向反射分布函数的粗糙面光散射偏振特性研究[J].中国激光,2013,40(12):225-230.
[4] 王晓,石顺祥,马琳.部分偏振光的表示方法[J].电子科技,2009,22(6):78-80.
[5] 吴健,杨春平,刘建斌.大气中的光传输理论[M].北京:北京邮电大学出版社,2005.
[6] 杨铁恒,赵永强,潘全,等.一种新的偏振光谱二向反射测量方法[J].光子学报,2008,37(12):2520-2524.
[7] 王霞,邹晓风,金伟其.粗糙表面反射辐射偏振特性研究[J].北京理工大学学报,2011,31(11):1327-1331.
[8] HYDE M W,SCHMIDT J D,HAVRILLA M J.A geome-trical optics polarimetric bidirectional reflectance distribution function for dielectric and metallic surfaces[J].Optics Express,2009,17(24):22138-22152.
[9] 冯巍巍,魏庆农,汪世美,等.涂层表面偏振双向反射分布函数的模型研究[J].光学学报,2008,8(2):290-294.
[10] FLYNN D S,ALEXANDER C.Polarized surface scattering expressed in terms of a bidirectional reflectance distribution function matrix[J].Optical Engineering,1995,34(6):1646-1650.
[11] 李景镇.光学手册[M].西安:陕西科学技术出版社,2010:1749-1769.
[12] 李学彬,胡顺星,朱文越,等.合肥、岳西、厦门和北京气溶胶谱分布特征分析[J].大气与环境光学学报,2011,6(2):154-162.
InfluenceofAtmosphericTransmissionandObjectReflectiononPolarizationPropertiesofCircularlyPolarizedLaserBeam
ZHAO Zhen-na1,2, YANG Yi2, WANG Jian-zhou3, TENG Yun-peng2,LI Cheng-jie2, SHEN Zhao-guo2, SUN Jun4
(1.Science and Technology on Electro-Optical Control Laboratory,Luoyang 471000,China; 2.Luoyang Institute of Electro-Optical Equipment,AVIC,Luoyang 471000,China; 3.Weinan Optoelectronics Technology Co.Ltd,Xi’an Heavy Equipment Manufacturing Group,Weinan 714000,China; 4.Nankai University Physics School,Tianjin 300071,China)
The influence of atmospheric transmission and object reflection on polarization properties of circularly polarized laser beam was studied.Based on the Monte Carlo method and with Stokes-Mueller matrix form,we used Mie scattering theory and polarized bidirectional reflection function model to trace the polarization state of each photon,made statistics and analysis to Stokes vector and polarization information of the final polarized light.The result of simulation shows that:With visibility of 23 km,distance of 100 km,target refractive index of 1.44+5.23i and surface roughness of 0.1 mm,the atmosphere has less influence on the polarization properties,while the target reflection has greater influence on the polarization properties;and the circular polarized light turns into elliptical polarized light at the receiving end.
laser ranging; polarization properties; atmospheric transmission; object reflection; Stokes vector
O436.3
A
1671-637X(2017)03-0068-05
2016-07-28
2016-09-13
国家自然科学基金(61575099)
赵帧娜(1992 —),女,河南灵宝人,硕士生,研究方向为激光测距光学系统设计。

