对地打击武器-目标分配问题的粒子群算法

王顺宏， 杨奇松， 王然辉， 赵久奋， 王国江

(1.火箭军工程大学，西安 710025; 2.中国人民解放军61683部队，北京 100094)

对地打击武器-目标分配问题的粒子群算法

王顺宏1， 杨奇松1， 王然辉2， 赵久奋1， 王国江2

(1.火箭军工程大学，西安 710025; 2.中国人民解放军61683部队，北京 100094)

对地打击武器-目标分配问题(BTG-WTA)是现代战争中的重要问题；相比于一般武器-目标分配问题，其规模更大，复杂程度更高。提出使用粒子群算法解决BTG-WTA问题，改进了粒子初始化、惯性权重选择等关键问题使其适应BTG-WTA问题模型，并结合具体算例进行了仿真。仿真结果表明，粒子群算法比解决WTA问题的经典算法速度更快、结果更优，具有更强的实际应用价值。

武器目标分配； 粒子群； 优化； 对地攻击

0 引言

武器-目标分配(Weapon-Target Assignment,WTA)也称火力分配或者目标分配，主要研究平台防空体系如何在已知来袭武器对己方目标威胁等级、破坏概率、己方防御武器的杀伤概率和受保护资源的重要程度等因素的条件下，按一定的分配原则、因素和约束条件，设计合适的武器分配方案，使得敌方来袭武器受到最大程度的打击且使己方受防御资源得到最好的保护[1]。目前WTA问题的模型研究和算法研究已经取得了较多成果，文献[2]提出了贪心遗传算法解决WTA问题；文献[3]提出了模糊多目标规划方法；此外，还有学者提出了基于满意决策的目标分配算法、基于遗传算法的动态武器目标分配策略以及基于免疫记忆的蚁群算法等，这都是对WTA问题有益的探索[4]。

当前所研究的WTA问题背景始终是防空拦截武器-目标分配，也有许多学者使用粒子群算法解决该问题，但是以对地打击作战行动为背景的研究非常少见。对地打击武器-目标分配是现代战争中的重要问题，从美军近几场局部战争中可发现，赢得战争的重要手段是大量打击和毁伤对方地面目标，以达到削弱其作战力量和瘫痪相关设施的目的，进而快速赢得战争。在该背景下的武器-目标分配问题称为BTG-WTA问题。与其他WTA问题相关文献本质区别在于问题的背景与模型不同,相比于防空拦截武器-目标分配问题，对地打击问题可选用的武器弹药组合较多，目标多样，导致其规模更大、复杂程度更高。若不能合理分配武器弹药，不仅会造成资源浪费，还有可能造成战机贻误。针对对地打击武器-目标分配问题建立合理的模型，设计高效的算法，是一项十分必要且紧迫的任务[5-9]。

1 BTG-WTA问题模型

BTG-WTA问题模型的假设如下:

1) 武器对目标的毁伤概率为综合毁伤概率，考虑了武器的突防概率、命中概率和毁伤概率等；

2) 同类武器对同类目标的综合毁伤概率相同。

基于上述假设，简要描述BTG-WTA问题：有N型武器打击M类地面目标，使得M类目标的毁伤分别达到C1,C2,…,CM。其中，N型武器数量分别为N1,N2,…,NN，其价值分别为V1,V2,…,VN；M类目标数量分别为M1,M2,…,MM;第i型武器打击第j类目标的毁伤概率为pij(i=1,2,…,N;j=1,2,…,M)。武器-目标最佳分配目标是以最小武器价值消耗满足目标毁伤要求，设第i型武器作用于第j类第k个目标的数量为mijk(k=1,2,…,Mj)，武器消耗价值为V，则BTG-WTA问题模型为

2 基本粒子群算法

粒子群优化(Particle Swarm Optimization,PSO)算法是近年发展起来的一种新的进化算法(Evolutionary Algorithm,EA)，与遗传算法相似，它也是从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质。但是粒子群算法比遗传算法规则更为简单，收敛速度更快；且没有遗传算法的“交叉”和“变异”操作，通过追随当前搜索到的最优值来寻找全局最优解。粒子群算法的研究依然处于初期，虽然在实际应用中证明是有效的，但是问题依然很多，还没有关于其收敛性和收敛速度等方面的数学证明，其理论和数学基础的研究还不够[10]。

PSO初始化为一群随机粒子(随机解)，然后通过迭代找到最优解。在每一次迭代中，粒子通过两个“极值”来更新自己。第一个是粒子本身所找到的最优解，即个体极值pbest；另一个极值是整个种群目前找到的最优解，即全局极值gbest。在找到这两个极值之后，便

可根据下式更新粒子的速度和位置。

式中：vk为当前粒子的速度；ω是惯性权重;xk是当前粒子的位置;pbest,gbest如前定义;r1,r2是介于(0，1)之间的随机数[11];c1,c2为学习因子，通常c1=c2= 2。每一维粒子的速度都会被限定在固定的范围之内，如果某一维粒子更新后的速度vk+1超过用户设定的最大速度vmax，则该维速度被限定为vmax；反之，如果小于设定的最小速度vmin，则vk+1取值vmin，通常vmin=-vmax。

3 解BTG-WTA问题的粒子群算法

3.1 粒子的结构和表示形式

为便于BTG-WTA问题的求解，首先要设计解的表示形式与粒子的结构。为使模型求解的过程更加清晰，用矩阵X=(xijk)N×M×Mj表示粒子位置，为与位置对应，粒子的速度用V=(vijk)N×M×Mj表示；xijk代表第i种武器对第j类第k个目标分配xijk个武器，xijk与第1章中mijk表达的意义一致，需满足式(2)所示条件，那么矩阵X便可以表示粒子的位置。每个粒子作为整个种群的一部分，在每次寻优过程中应该携带该粒子的当前位置信息以及历史寻优信息，该信息通过粒子结构来体现，如图1所示。

图1 粒子结构Fig.1 Particle structure

3.2 惯性权重系数的选择

惯性权重系数ω可以有效调整算法的搜索范围，这对于搜索空间巨大且容易陷入局部极值的BTG-WTA问题至关重要。权重系数ω越大，算法的全局搜索能力越强；反之，局部搜索能力较强，搜索精度较高。权重系数ω一般是在算法开始前即设定ω的递减规律，但无法根据粒子位置的更新规律进行自主调节[12]。为适应BTG-WTA模型求解，本文以10次迭代为一个阶段，设定权重系数根据粒子位置及最优值的变化规律进行自主更新，流程如图2所示。

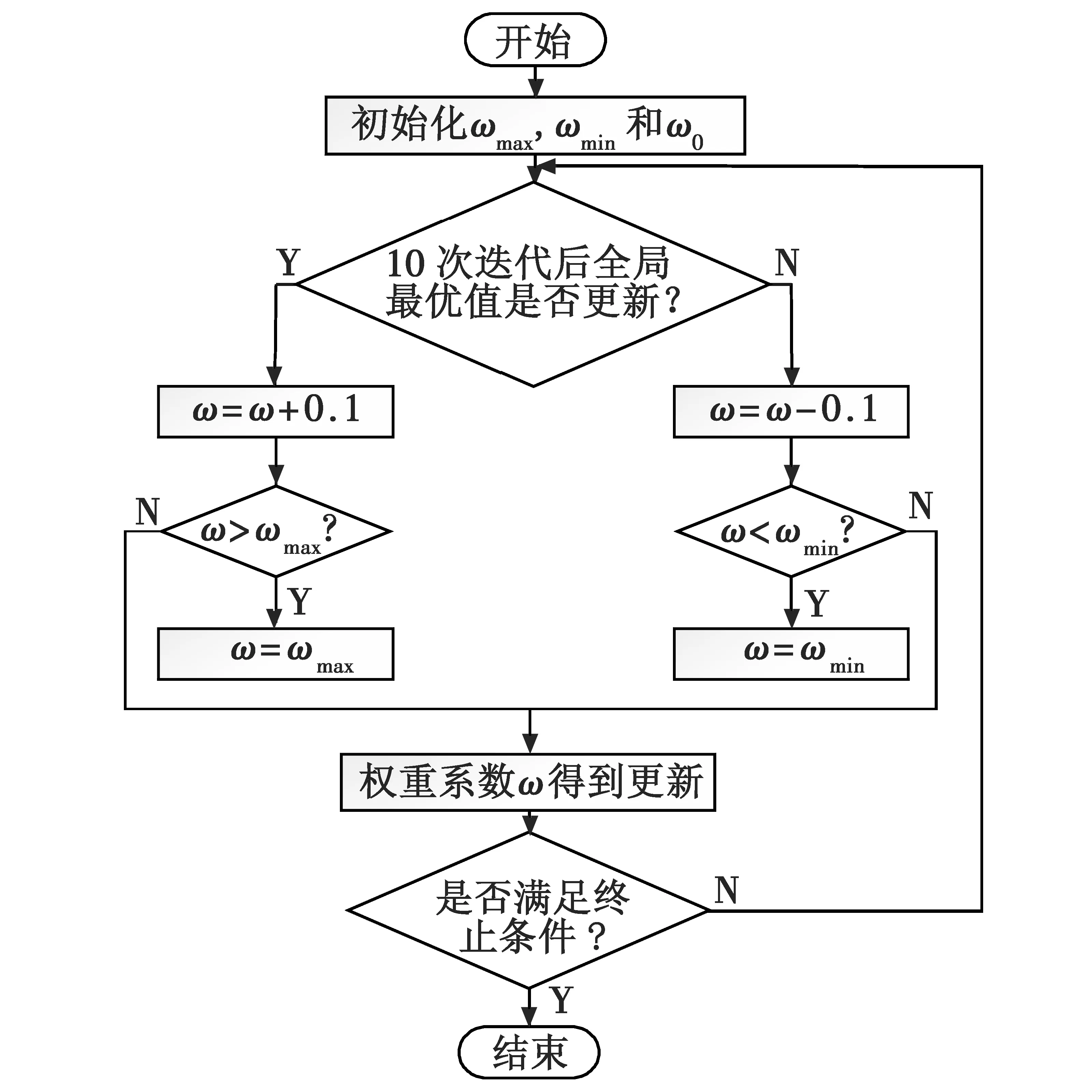
图2 惯性系数更新规律Fig.2 Law of inertia weight succession

3.3 适应度函数

由于BTG-WTA问题所含的约束条件较多，寻求一定数量可行解的过程较慢，因此直接解决此问题效率必定不高。本文将约束条件处理成罚函数的形式，以加快整个算法的寻优进程。引入惩罚因子W，其为量级较大的正整数；引入惩罚程度K1和K2，分别代表对式(2)中第一和第二个约束条件的惩罚程度，即可计算出[13]

式中:

在算法优化的过程中，需要根据解的优劣来控制优化的方向，解的优劣由适应度函数进行评价。本文设适应度函数为

式中，X代表一个完整的分配方案。在优化过程中，获取每一次的分配方案之后，便可根据式(5)～式(7)计算出惩罚程度，然后利用式(8)计算该粒子的适应度。

3.4 初始化粒子速度范围

由粒子群算法优化的基本步骤可知，粒子的位置根据粒子的速度进行更新。因此，粒子更新的速度必须受到一定的限制，其大小必须与粒子位置的量级相适应，这直接影响了算法寻优的速度与精度。结合BTG-WTA问题的模型，X中的每一个xi jk均是由武器的数量和目标的数量决定的，其具体数值必然根据所有武器平均于每个目标上的数量上下浮动，本文利用式(9)决定粒子速度的范围，取得了较好的效果。

式中:[·]代表不大于·的最大整数。

3.5 放宽约束条件产生初始种群

在模型有解的条件下，适当放宽武器数量约束后的模型最优解与原模型一致。在有约束的情况下，放宽约束条件可以大大加快可行解的生成速度。将约束条件处理成罚函数之后，初始解的产生不再受约束条件的限制，但放宽武器数量约束依然可以发挥较强作用。本文按照式(10)更加宽松的武器数量，利用粒子群算法迭代n1次产生的各粒子最优位置为初始种群，这样的约束使得初始解的搜索范围更广，以更多的方向往最优解接近，从而避免被严格的约束所阻隔，降低了后续寻优中陷入局部最优解的概率[14]。

初始解的优劣将直接影响算法的效率和最终结果，因此初始解X0在随机产生的过程中必须具有一定的方向性，要尽可能满足约束且往最优解的方向靠拢。本文采用式(10)所示算法对初始解和速度加以控制。

式中：ω1，ω2为[0,1]区间内的随机数；α为[0.5,1]区间内的随机数。按照式(11)依次对每一个xijk和vijk赋初值，形成完整的初始解X0和V0。

3.6 模型求解

3.1～3.5节解决了粒子群算法求解BTG-WTA模型的关键问题，综上所述，本文解决BTG-WTA问题的算法流程如图 3所示。

图3 改进PSO算法解算流程Fig.3 Resolving process of the improved PSO

本文使用的粒子群算法步骤可以描述为：

1) 放宽武器数量约束，设置相应适应度函数F(X)，初始化群体；

2) 利用粒子群算法迭代n1次(算法关键问题与后续过程一致)，以各粒子的最优位置为初始种群；

3) 还原约束条件，调整适应度函数；

4) 计算每个粒子的适应度F(X)，更新pbest和gbest；

5) 按照式(3)和式(4)更新粒子的位置和速度；

6) 检验是否满足结束条件(设定迭代次数n2)，如果满足，则停止迭代输出最优解，否则，转至步骤4)。

4 仿真算例

为了验证本文改进粒子群算法解决BTG-WTA问题的有效性，使用算法对4个不同规模的案例进行解算，并与改进的遗传算法[15]计算结果进行比较。有5类武器弹药D1，D2，…，D5，对地面6类目标B1，B2，…，B6进行打击，不同案例的武器信息如表1所示，目标信息以及对每类每个目标的要求毁伤级别如表2所示，武器对目标的毁伤概率信息如表3所示。

各案例的问题规模如表4所示。设置粒子群算法的粒子数为100，产生初始种群的迭代次数n1为1000，终止条件设迭代次数n2为30 000；权重系数最大值ωmax取值1.2，最小值ωmin取值0.1，初始值ω0取值0.9。分别使用改进遗传算法和本文所述粒子群算法对各案例进行解算，两种算法各测试100次后取测试过程中的最优解。为使解算结果更为直观，绘制了如图4和图5所示的时间和武器消耗价值与变量个数的关系折线图。

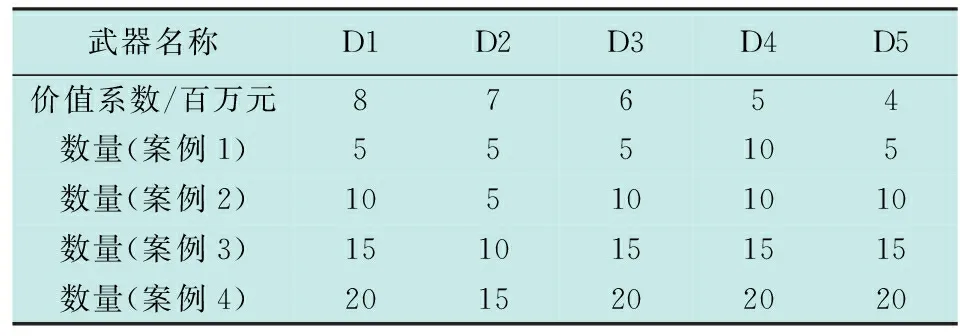
表1 武器信息

表2 目标信息

表3 毁伤概率信息

表4 问题规模

图4 解算时间与变量个数的关系Fig.4 Resolving time vs number of variables

由图4、图5粒子群算法的计算结果可以看出，没有出现量级较大的武器消耗价值，这证明所得解均是满足约束条件的。由图4和图5可以看出，与改进遗传算法的计算结果相比较，粒子群算法收敛更快，结果更优；随着问题规模的增加，粒子群算法效率和结果的优势更加明显。而且，粒子群算法解算上述不同规模的问题时，参数设置都是一样的，只需根据实际任务需要，适当改变算法的迭代次数以调整模型解算时间，这使得整个模型解算过程操作简便，更加适应工程实际的需要。

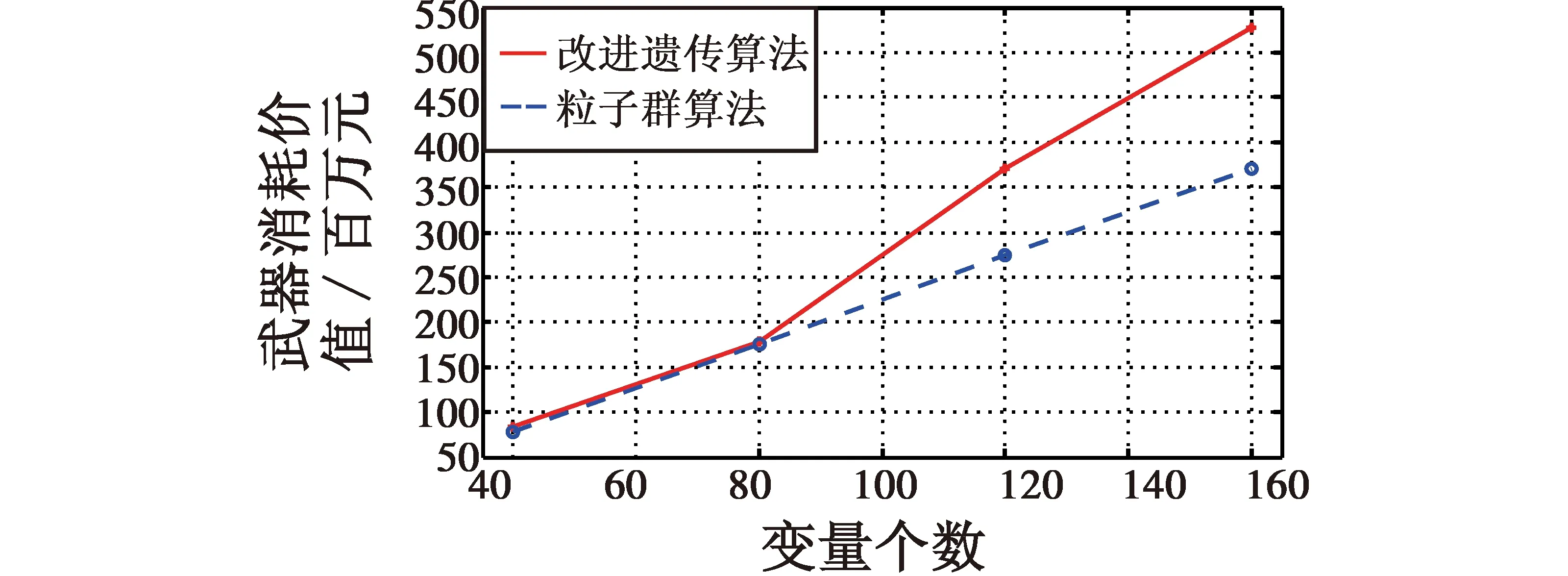
图5 武器消耗价值与变量个数的关系Fig.5 Consumption value vs number of variables

5 结束语

对地打击武器-目标分配是现代战争中的重要问题，本文尝试用改进粒子群算法对其进行解算，为该类型的WTA问题研究提供了一种新的思路。从本文仿真结果看，本文算法易于实现、效率更高并且结果更优，这使得其更加适应现代战争中对地打击武器-目标分配问题的巨大规模，以及信息化条件下快速决策的需要,但由于对地打击问题模型与算法的探索还处于初期阶段，更多细致工作有待进一步开展。

[1] 蔡怀平，陈英武．武器-目标分配(WTA)问题研究进展[J]．火力与指挥控制，2006，32(12):11-15.

[2] 张海兵,徐诚,李世永.贪心遗传算法及其在武器目标分配问题中的应用[J]．弹道学报，2007,19(2):40-43.

[3] 陈建虎，吕志明.武器-目标分配的模糊多目标规划[J].武器装备自动化，2007,26(6):3-4.

[4] 李勇君，黄卓，郭波．武器-目标分配问题综述[J]．兵工自动化，2009，28(11)：1-4.

[5] MORRIS R D.Weaponeering:conventional weapon system effectiveness[M].Reston:American Institute of Aeronautics and Astronautics,INC,2004.

[6] LOYD S P,WITSENHAUSEN H S.Weapons allocation is NP-complete[C]//Proceedings of the IEEE Summer Computer Simulation Conference,Reno,1986:125-139.

[7] LEE Z J,SU S F,CHOU Y L.Efficiently solving general weapon-target assignment problem by genetic algorithms with greed eugenics[J].IEEE Journal on Systems,Man, and Cybernetics-Bart B Cybernetics,2003,33(1):119-120.

[8] PATRICK A,HOSEIN M A.Some analytical results for the dynamic weapon-target allocation problem[R].Cambridge:LIDS-P-1944,1990.

[9] CULLENBINE C.A tabu search approach to the weapon assignment model[R].Dayton:AFIT/GOR/ENS/00M-08,2000.

[10] 刘衍民.粒子群算法的研究及应用[D].济南:山东师范大学,2011.

[11] 高尚,杨静宇.武器-目标分配问题的粒子群优化算法[J].系统工程与电子技术,2005,27(7):1250-1252,1259.

[12] 杨飞,王青,侯砚泽.基于整数域改进粒子群优化算法的多平台武器目标分配[J].兵工学报,2011,32(7):906-912.

[13] 李赵阳.基于粒子群算法的武器-目标分配问题求解[D].长春:吉林大学,2009.

[14] 刘爽英,韩燮.一种求解武器目标分配问题的量子粒子群算法[J].计算机科学,2013,40(2):235-236，248.

[15] 喻寿益,邝溯琼.嵌套式模糊自适应遗传算法[J].控制工程,2010,17(1):75-79.

ParticleSwarmOptimizationBasedWeapon-TargetAssignmentforAttackingGroundTargets

WANG Shun-hong1, YANG Qi-song1, WANG Ran-hui2, ZHAO Jiu-fen1, WANG Guo-jiang2

(1.Rocket Force University of Engineering,Xi’an 710025,China; 2.No.61683 Unit of PLA,Beijing 100094,China)

Weapon-Target Assignment for attacking ground targets (BTG-WTA) is an important issue in modern warfare,which has larger scale and is more complicated than the ordinary weapon-target assignment.Particle Swarm Optimization (PSO) algorithm is used for solution of the BTG-WTA.The key issues,such as particle initialization and inertia weight selection,are improved for adaptable to BTG-WTA model,and simulation is made to an example.The results of simulated experiment indicate that PSO is more efficient than the classical algorithm for BTG-WTA,and thus has great application value.

weapon-target assignment; particle swarm; optimization; ground target attacking

O22

A

1671-637X(2017)03-0036-05

2016-03-21

2016-04-22

王顺宏(1975 —),男,甘肃天水人,博士，副教授,硕导,研究方向为弹道设计。