针对含噪信号的自适应跟踪微分器改进研究

张 帆， 徐华中， 向 云， 汪赛力

(武汉理工大学自动化学院，武汉 430070)

针对含噪信号的自适应跟踪微分器改进研究

张 帆， 徐华中， 向 云， 汪赛力

(武汉理工大学自动化学院，武汉 430070)

跟踪含噪信号时，传统的自适应跟踪微分器会有扰动引入到速度因子和滤波因子参数中，导致系统跟踪紊乱从而跟踪到噪声。针对这个问题，分析了噪声引入的原因，研究了传统自适应跟踪微分器的性能，提出了将跟踪间距的滑动窗口标准差估计作为输入的自适应函数来调整滤波因子和速度因子的改进跟踪微分器(IATD)的实现方法。仿真结果表明，IATD具有精确的参数调整能力，噪声条件下拥有更快的跟踪速度，同时在宽范围信噪比条件下也具有更强的噪声抑制能力。

含噪信号； 自适应跟踪微分器； 滑动窗口标准差； 噪声抑制

0 引言

在控制和测量领域，从噪声环境中提取或者恢复有效的原始信号对于控制系统性能至关重要[1-2]。传统方法采用维纳滤波器和卡尔曼滤波器，计算量很大，为提高滤波器设计的简便性、实用性[3]，1994年,韩京清等人[4]提出跟踪-微分器(TD)的概念，2004年，武利强等人[3]研究了跟踪微分器的滤波性能，解决了由不连续或带随机噪声的量测信号中提取连续的有效信号及其微分信号问题。跟踪微分器具有良好的跟踪性能和抗干扰能力，但随着信号与混杂噪声的变化，跟踪的速度和噪声抑制能力就会一定程度地减弱；为此，2002年，景奉水等人[5]根据最优控制原理，提出了依据跟踪信号与输入信号的间距去控制速度因子的线性自适应函数，一定程度上提高了跟踪微分器的快速性，但是并未考虑滤波因子，且一旦信号含噪声，速度因子很容易受干扰；2009年，QIAO G等人[6]同样忽略滤波因子，提出了将S形函数作为自适应控制函数，在输入信号较小时会产生滞后；随后，范红伟等人[7]考虑了低噪声环境下跟踪误差的变化规律，结合统计方法，于2012年提出了控制速度因子和滤波因子变化的概率函数，这样的设计同时考虑速度因子和滤波因子，但是概率函数由跟踪信号的微分来控制，一旦混杂噪声，便迅速引入概率函数中，影响跟踪的性能。

本文受统计学中运用标准差法分析、处理数据得到有效估计的启发，引入滑动窗口标准差，实现跟踪间距的准确估计，避免了自适应参数中的扰动；为了更快地调整到最佳跟踪状态，对文献[5]提出的自适应结构进行了修改，兼顾跟踪的快速性和收敛性，实现了改进跟踪微分器(Improved Adaptive Tracking Differentiator,IATD)的设计；结合文献[7]，提出了更全面的IATD的性能评估方案。通过仿真验证了IATD的有效性及相对其他跟踪微分器的优势。

1 问题分析

跟踪微分器(Tracking Differentiator,TD)是针对连续信号进行跟踪并提取微分信号的数值算法，而实际应用更多的是其离散形式[8]，即

(1)

以下是对跟踪微分器结构的进一步说明

(2)

式中：x1和x2为二阶系统的状态变量；f为最速综合控制函数;sat(x,δ)为饱和函数；v为输入信号；x1为v的跟踪信号；x2为x1的导数；h为采样周期；h0为滤波因子，决定滤波的轻重程度；r为速度因子，决定跟踪速度的快慢。r越大，系统跟踪速度越快，适当地选取h，可以很好地滤除噪声，但h过大，又会增加相位损失，因此参数整定需同时考虑两方面的性能[9]。

由文献[4]可知，只要速度因子和滤波因子选取适当，跟踪微分器可以任意精度提取原始信号的最佳逼近；人工经验法可选择可用的速度因子和滤波因子，但无法选择指标性优化参数[10]；由文献[3-7]可知，在实际系统中，根据跟踪微分器的跟踪信号及其微分信号，找到与速度因子及滤波因子之间的定性关系，便可设计出自适应调整参数的跟踪微分器。

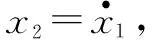
(3)

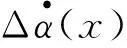
(4)

由此进一步分析可知，只有输入理想时，自适应控制函数用于跟踪微分器才可获得理想效果；当输入含有噪声时，自适应控制函数用于跟踪微分器便会引起系统的震荡，削弱跟踪性能。

2 IATD的改进设计

2.1 TD,ATD的性能

首先分析传统自适应跟踪微分器的性能。文献[5]根据最优控制理论提出自适应跟踪微分器(记为ATD1)，r值随跟踪信号和输入信号间距做线性变化，如

r=r0+k|x1-v|

(5)

式中,k为控制系数。

文献[7]提出自适应跟踪微分器(记为ATD2)，让r和h0作为跟踪信号的微分概率函数,如

(6)

式中：γ1和γ2为概率系数；A和B分别为速度因子的起始值和变化范围。

根据上文分析，式(5)和式(6)均形如式(4)，输入含噪声时，对应的速度因子和滤波因子也会引入噪声。下面仿真分析TD，ATD1及ATD2的性能。设原始信号v=0.2sin 5t，加入方差为0.01的高斯噪声，积分步长h=0.000 1，初始滤波因子h0=0.001，速度因子r=30。首先研究跟踪性能，如图1所示。由图1可知，TD的跟踪存在较大滞后；ATD1的快速性有所提高，相比TD滞后减小；ATD2响应很快，但完全跟踪了噪声。

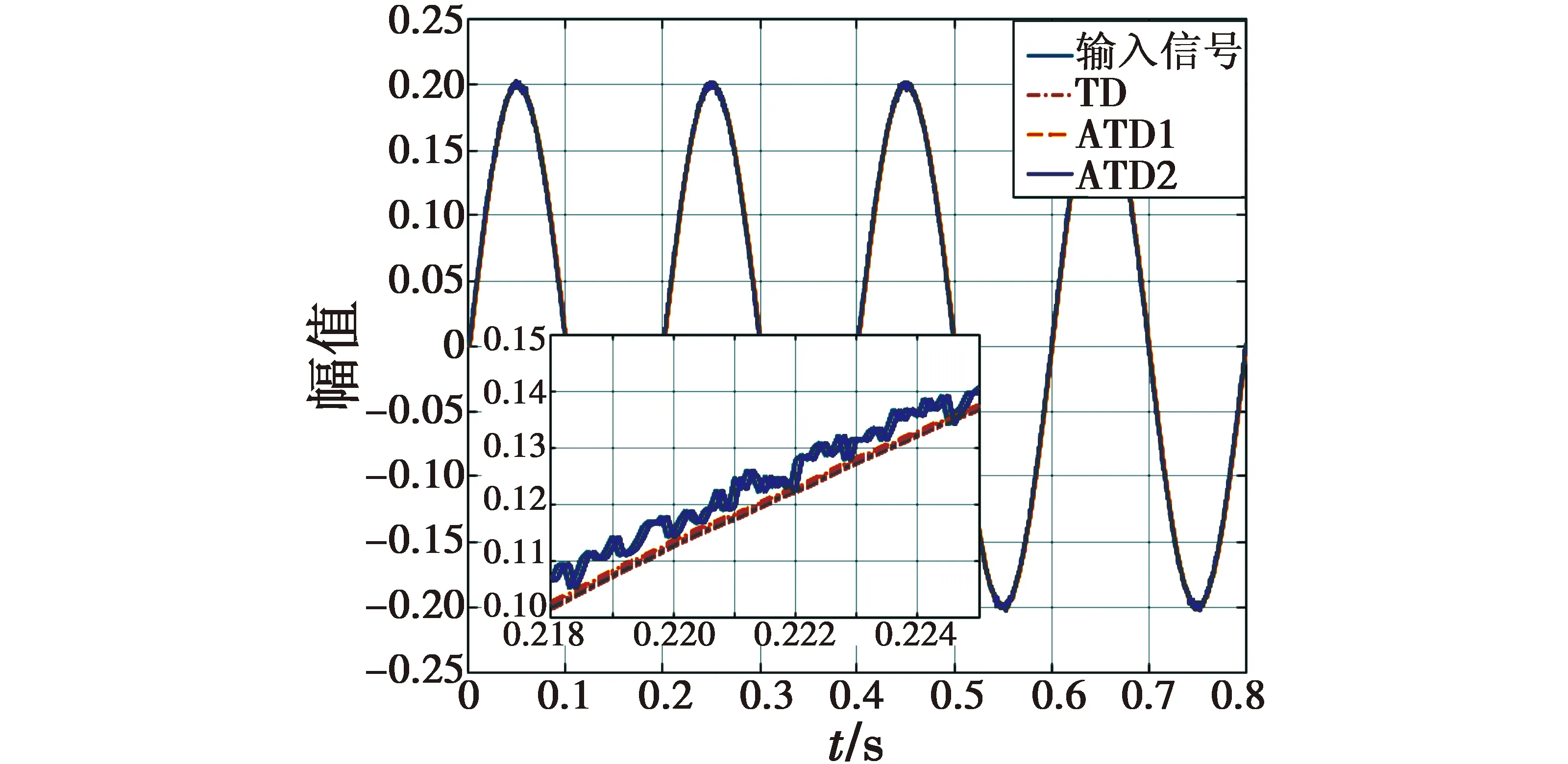
图1 TD，ATD1与ATD2跟踪对比Fig.1 Tracking performance comparison of TD,ATD1 and ATD2

为进一步分析跟踪参数的噪声引入情况，绘制了3种跟踪微分器速度、滤波因子曲线，如图2所示。图2a中TD参数不变，同初始整定速度、滤波因子；图2b中ATD1虽然不断调整速度因子的变化，但震荡严重，且滤波因子不可控；图2c中ATD2的速度、滤波因子也存在明显噪声干扰。

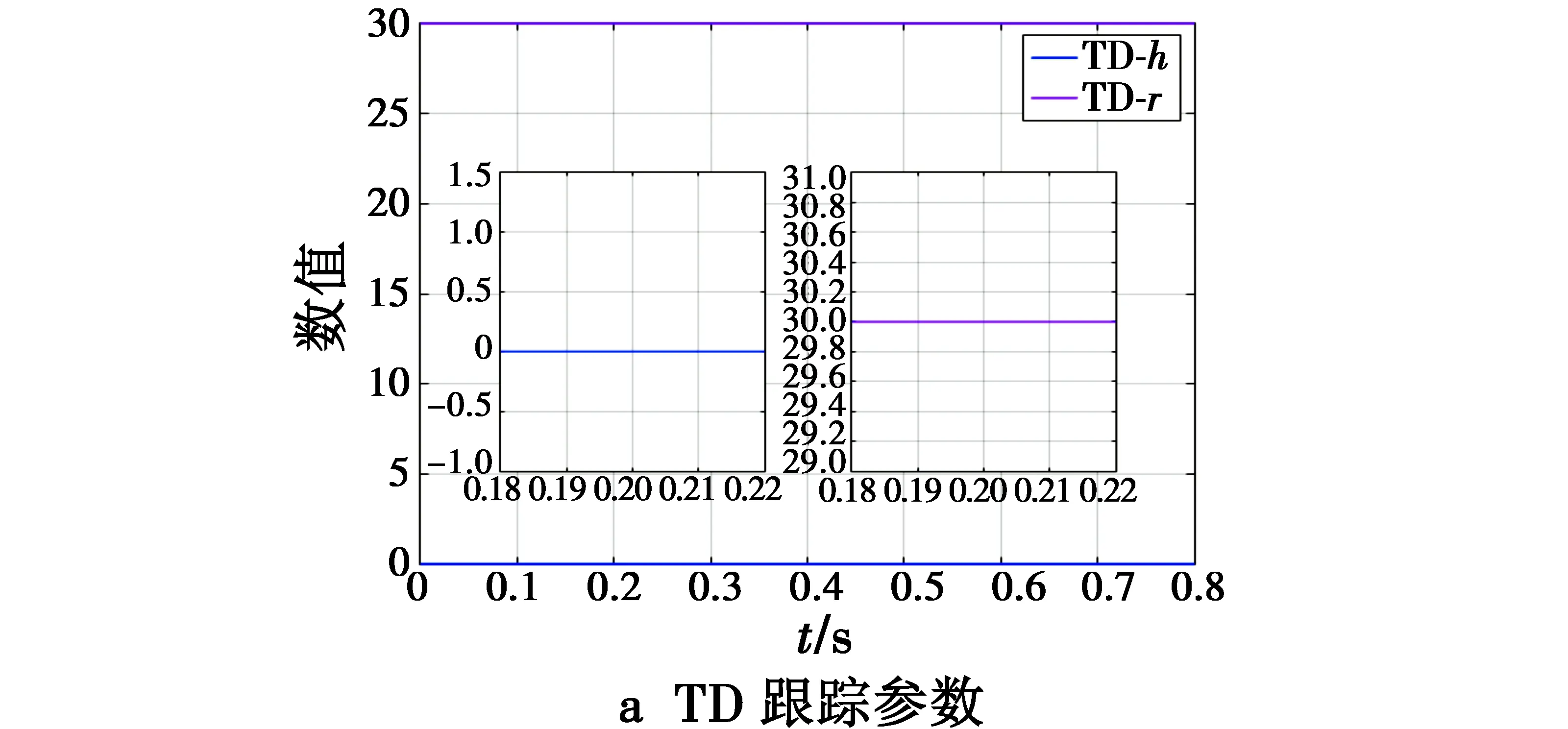
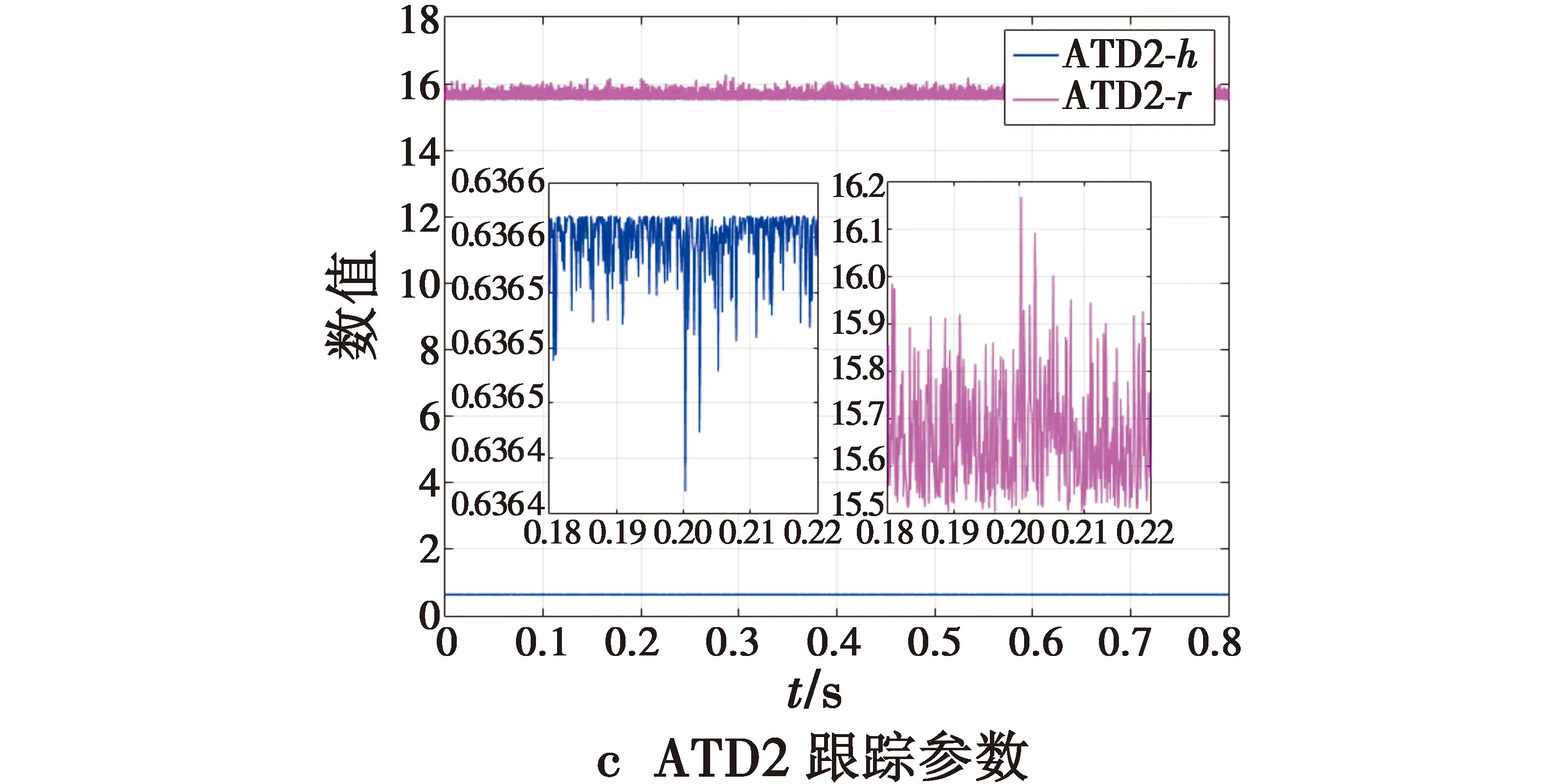
图2 跟踪微分器参数对比Fig.2 Tracking parameter comparison

根据上文可知：1) 采用跟踪信号的微分构成的自适应控制函数，在提高跟踪响应的同时，也提高了噪声跟踪的响应；2) 滤除自适应控制函数中的噪声，才能更快地调整到最佳跟踪性能。

2.2 滑动窗口标准差估计

针对上述观点，做以下分析，假设输入信号v由原始信号φ和高斯噪声n构成如下

v=φ+n

(7)

式是:φ=Asinωt;n=rand(B)。

所谓高斯噪声，一般指均值为零的白噪声的随机过程，若其自相关序列为

(8)

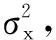
针对式(7)的输入信号，假设存在理想跟踪微分器，跟踪信号为x1=Asinωt，跟踪间距为

|x1-v|=|rand(B)|。

(9)

考虑输入均匀分布的高斯白噪声，即理想跟踪效果下跟踪间距应为常数，而ATD1和ATD2的速度、滤波因子是扰动的。为此，基于统计学方法[11]，提出滑动窗口标准差(Moving Window Standard Deviation,MWSD)估计方法，其算式为

(10)

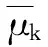
图3 MWSD估计Fig.3 Estimation of MWSD

2.3 IATD的设计

在跟踪微分器跟踪过程中，跟踪间距与速度、滤波因子存在定性关系,所以设计这样的自适应函数,如下式

(11)

式中,std()为滑动窗口标准差估计函数，表示在跟踪含高斯噪声的信号时，对跟踪间距到平均值为零的离散程度的估计。跟踪间距增大时，首先跟踪速度加快，同时滤波加重，跟踪间距又随之下降；跟踪间距减小时，滤波减轻，跟踪速度下降，TD滞后，跟踪间距又随之增大。总之，跟踪间距及两个参数互相不断调节，当间距趋于参考间距值并稳定时，速度、滤波因子最佳。 将式(11)代入式(1)，可得改进的自适应跟踪微分器。式(11)中,kr为速度因子控制系数，kh0为滤波因子控制系数，其他各参数意义同式(1)，即IATD是TD的拓展，也可以说，IATD是对ATD1结构上的改进，结构对比如图4所示。

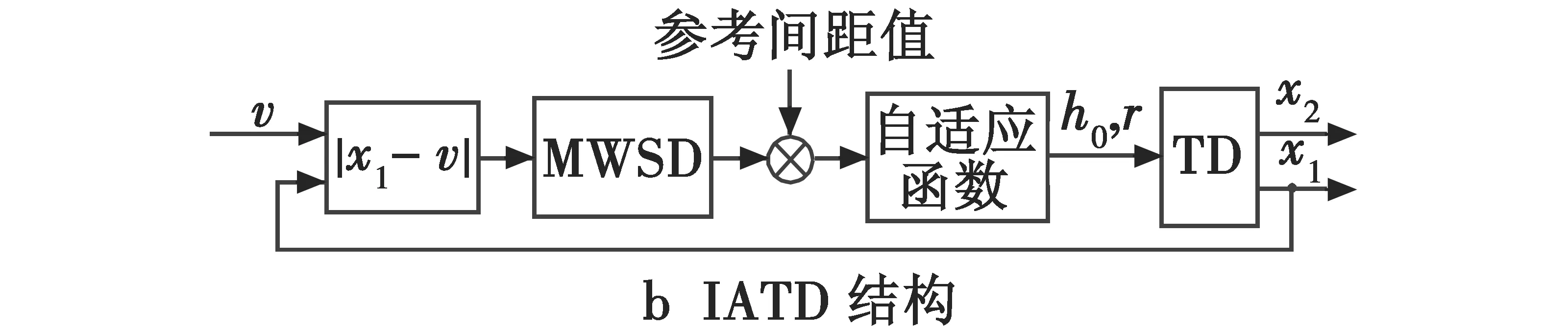
图4 ATD1和IATD结构对比Fig.4 Structure of ATD1 and IATD

3 仿真验证

为验证IATD的效果，将IATD与TD，ATD1以及ATD2仿真比较。取信噪比为40 dB的高斯噪声，原始信号幅值为0.2，频率为5 Hz；跟踪微分器的初始速度因子r=30，滤波因子h0=0.001。

图5a为对含有噪声的正弦信号的跟踪，结合图1可知，相比之下，IATD具有最好的性能；结合图5b可知，IATD的跟踪误差变化平稳，在快速响应的同时，有良好的噪声抑制能力。

图6为IATD跟踪上文所述条件下输入信号时速度因子和滤波因子的变化曲线。由图可知，相比图2中TD,ATD1及ATD2的参数变化，IATD仅含有少量的噪声，很好地避免了震荡的产生。

文献[7]提出跟踪性能的评价指标失真因子概念(用P表示，包括滞后因子Q和噪声因子R，即P=Q+R，P越低即跟踪性能越好)，为进一步验证IATD在宽范围混杂噪声下的性能，使输入信号的信噪比在20～70 dB的范围内变化，采用失真因子作为评价指标完成多组仿真，横向对比TD，ATD1，ATD2及IATD的性能，绘制图7。由图7可知，在宽信噪比范围内，TD的失真因子较差;ATD1得到一定的改善；ATD2具有极低的失真因子，但结合图1和图2c可知，是跟踪到了噪声信号所导致；IATD失真因子较TD,ATD1得到很大的改善，也就是说，IATD在宽信噪比范围内，具有良好的噪声抑制能力。

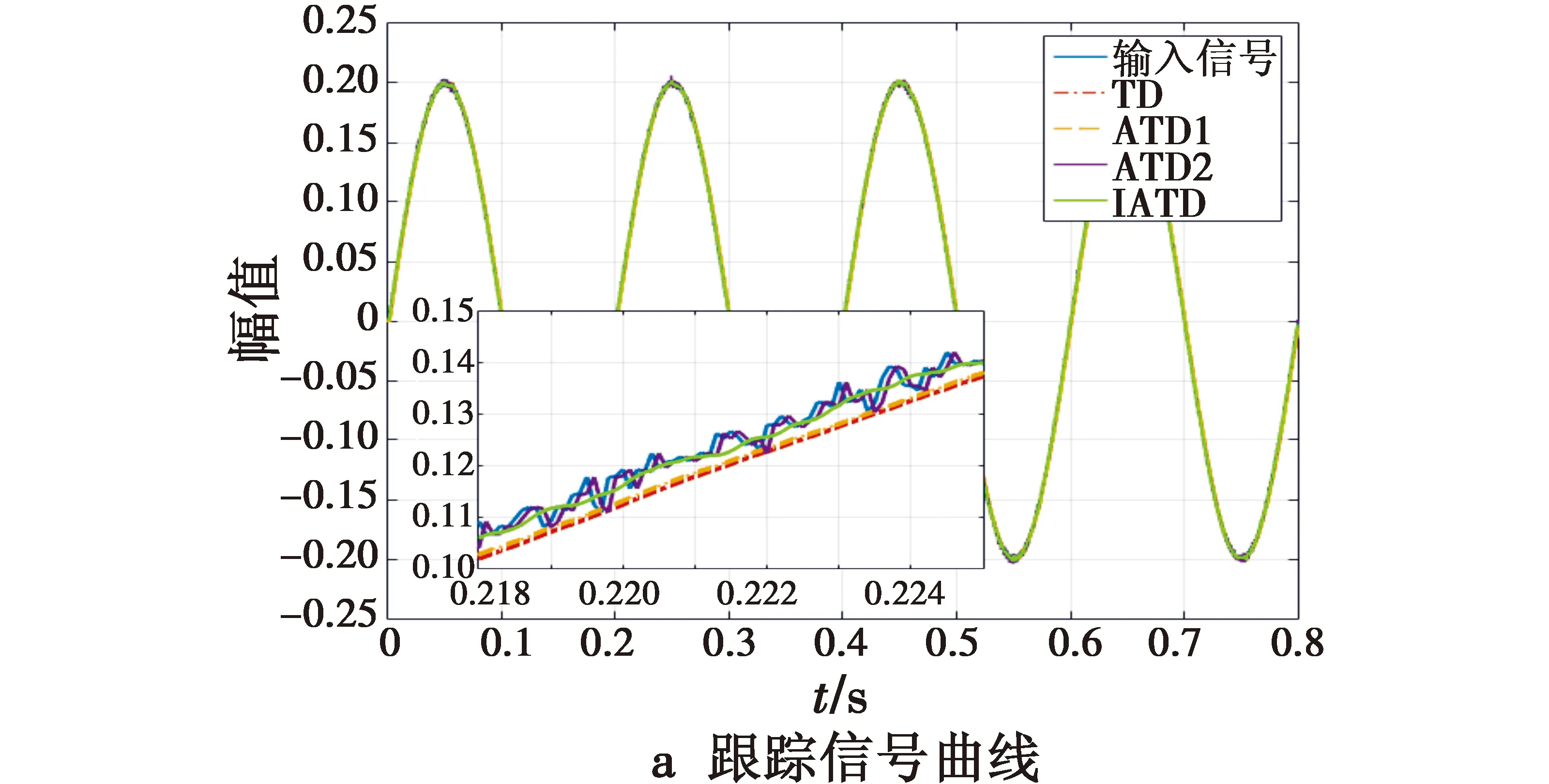
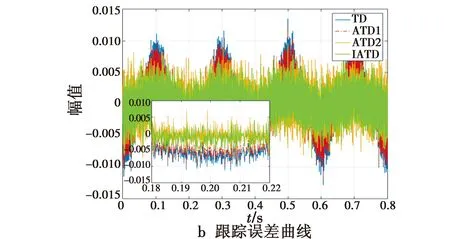
图5 IATD与TD，ATD1，ATD2跟踪性能对比Fig.5 Tracking performance of TD,ATD1,ATD2 and IATD

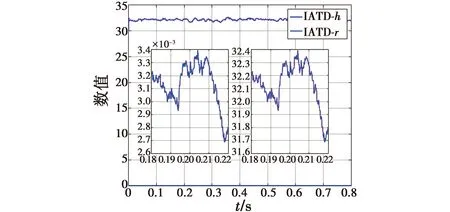
图6 IATD跟踪参数Fig.6 Tracking parameter of IATD

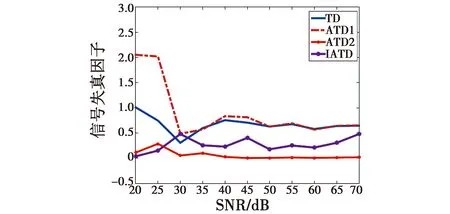
图7 宽信噪比范围内跟踪性能对比Fig.7 Tracking performance comparison of wide range of signal-noise ratio

4 结束语

本文在分析噪声引入原理、研究传统的自适应跟踪微分器跟踪性能的基础上，提出了一种针对含噪信号的自适应跟踪微分器改进的实现方法。该方法基于滑动窗口标准差估计算法，对跟踪微分器速度、滤波因子中引入的噪声进行抑制，兼顾系统跟踪的快速性和收敛性，在宽信噪比范围内具有很好的噪声抑制能力，仿真证明了该方法的有效性。该方法适用于标量系统，对于矢量系统的应用，亦可进一步推导研究。

[1] 姚天任,孙洪.现代数字信号处理[M].武汉:华中科技大学出版社,1999.

[2] 陈怡然,孙秀霞,彭建亮.一种简洁的离散快速无震荡跟踪-微分器的设计[J].电光与控制,2011,18(1):77-81.

[3] 武利强,林浩,韩京清.跟踪微分器滤波性能研究[J].系统仿真学报,2004,16(4):651-652,670.

[4] 韩京清,王伟.非线性跟踪-微分器[J].系统科学与

数学,1994,14(2):177-183.

[5] 奉景水,梁自泽,侯增广,等.自适应跟踪微分器的研究[C]//第二十一届中国控制会议论文集,2002:319-322.

[6] QIAO G,SUN M,ZHANG R,et al.An improved self-adaptive tracking differentiator[C]//Information and Automation,2009:22-24.

[7] 范宏伟,王洪福,张伟明.基于跟踪-微分器的宽动态测速系统设计[J].电光与控制,2012,19(8):59-62.

[8] 韩京清,袁露林.跟踪-微分器的离散形式[J].系统科学与数学,1999,19(3):268-273.

[9] 韩京清.自抗扰控制技术-估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.

[10] 冯长辉,齐晓慧,苏立军,等.四旋翼无人机TD-PD控制律设计[J].电光与控制,2016,23(3):36-40.

[11] 杨辉华,郭拓,马晋芳，等.一种近红外光谱在线监测新方法及其在中药柱层析过程中的应用[J].光谱学与光谱分析,2012,32(5):1247-1250.

ImprovementonAdaptiveTrackingDifferentiatorforNoisySignal

ZHANG Fan, XU Hua-zhong, XIANG Yun, WANG Sai-li

(School of Automation,Wuhan University of Technology,Wuhan 430070,China)

When tracking noisy signals with traditional adaptive tracking differentiator,disturbance may be introduced into rate factor and filtering factor of the differentiator and leads to disorder and tracking to the noise.To solve this problem,the cause of noise was analyzed,performances of adaptive tracking differentiators were studied,and an Improved Adaptive Tracking Differentiator (IATD) was proposed.By using the adaptation function taking the Moving Window Standard Deviation (MWSD) estimation of track spacing as input,the IATD could adjust the rate factor and filtering factor optimally.Simulation indicates that IATD can adjust factors more accurately and rapidly with noisy input,and has better noise restraining ability in wide range of signal noise ratio.

noisy signal; adaptive tracking differentiator; moving window standard deviation; noise restraining

TP273; U467.4

A

1671-637X(2017)03-0060-04

2016-03-08

2016-04-27

国家国际科技合作专项(2012DFA11180)

张 帆(1991 —),男，内蒙古呼和浩特人，硕士生，研究方向为自抗扰控制、信号处理。