某伺服机构健康评估方法研究

张晓雨, 何华锋， 郑建飞， 董海迪

(火箭军工程大学,西安 710025)

某伺服机构健康评估方法研究

张晓雨, 何华锋， 郑建飞， 董海迪

(火箭军工程大学,西安 710025)

健康等级不同的装备在维护保养和执行任务时应采取不同的方案。当前装备的测试评估仍然采用“是非制”，即通过测试仅能判定装备正常与否，缺少对其健康等级的评判。针对这个问题，以某伺服机构为研究对象，提出一种基于改进证据理论的健康状态评估方法,该方法首先确定能够全面表征伺服机构健康状态的参数集合，利用归一量化的方法对测试数据进行处理。然后基于改进的证据理论，对处理后的各项参数隶属度进行融合，从而得到伺服机构的健康状态等级。最后，通过对某伺服机构的实例分析，验证了所提方法的有效性和应用价值。

伺服机构； 武器装备； 健康评估； 测试数据； 改进证据理论

0 引言

目前，对武器装备状态的评估仍采用“是非制”，即只要装备通过了测试，就认为该装备合格，这种方法存在一定的局限性，无法得到装备健康状态的具体等级。装备的健康状态影响装备战备值班任务的安排，并且不同状态的装备应采取不同的维护保养方案[1-3]。针对上述问题，本文以某伺服机构为例，按照性能要求对其健康状态等级进行划分，提出了一种基于改进证据理论的多指标融合伺服机构健康状态评估方法。

1 健康评估体系构建

1.1 健康指标分析

伺服机构的测试项目比较多，不同的项目表示不同的性能，建立全面、合理的健康指标体系是对伺服机构进行健康评估首先要解决的问题。

建立健康指标体系既要考虑全面性，又要兼顾不相容性。伺服机构性能测试内容主要包括状态参数、静态特性和动态特性[4]。状态参数的好坏一般都可以在伺服机构控制性能中表征出来。根据测试内容和评估原则，健康指标体系主要包括静态特性和动态特性[5]两方面，每个特性又能够细化为更详细的指标，由此建立如图1所示的伺服机构健康指标层次结构模型。

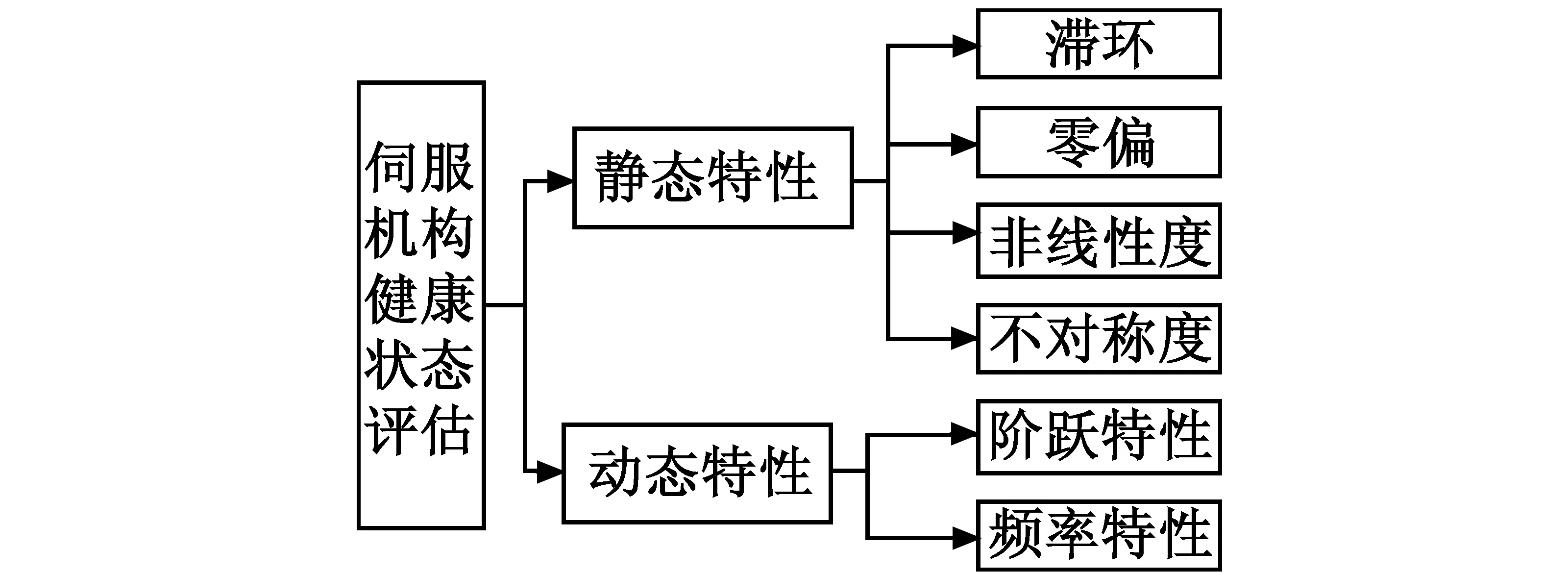
图1 伺服机构健康指标层次结构模型Fig.1 Health indicators hierarchical model of servo mechanism

1.2 健康状态分级与隶属函数表示

对伺服机构进行评估之前，需要先划分伺服机构的健康状态等级。根据性能要求，可将伺服机构(或各项指标)的合格状态划分为良好、较好、堪用和拟故障等4种状态等级。伺服机构各状态之间没有具体的界限，只有模糊的过渡区域，根据装备实际退化状况和相关专家经验[6]，状态隶属度的判别采用了模糊三角函数的方法，如图2所示。

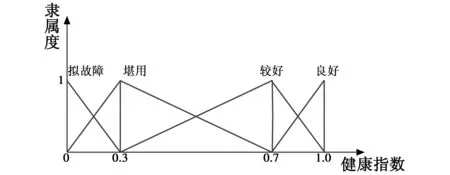
图2 模糊三角隶属度函数Fig.2 Triangular fuzzy membership function

良好状态表示伺服机构的健康状态非常好，能够满足长期服役的要求。其隶属度函数为

(1)

较好状态表示伺服机构健康状态尚可，虽然跟良好状态相比有一定恶化，但影响不太严重。其隶属度函数为

(2)

堪用状态表示伺服机构健康状态退化较大，但是还满足正常使用要求。其隶属度函数为

(3)

拟故障状态表示伺服机构已经进入故障高发期，尽管测试指标显示正常，但需要纳入维护规划。其隶属度函数为

(4)

2 测试数据的归一量化处理

伺服机构属于长期贮存装备，仅凭某次测试数据来评估其健康具有一定片面性。为此，本文提出一种对测试数据进行归一量化处理的方法。归一量化处理主要包括3项：当前数据和历史数据均值的比较，当前数据和上次数据的比较以及当前数据和给定标准值的比较。下面以当前测试数据和历史测试数据均值的归一量化为例进行说明。

首先，计算当前测试数据与历史测试数据均值的偏差的绝对值，表达式为

δh=|x-xh|

(5)

式中：x表示本次值;xh表示历史测试数据均值。

然后，计算归一量化值λh。算式采用了半梯形函数的方法，表达式为

(6)

式中，δ0为最大误差限。

对于本次和上次测试值比较值的归一量化值λl以及与给定指标值的比较值的归一量化值λs，均可参考上述方法进行处理。

得到归一量化值后，接下来的工作就是根据上述3项归一量化值计算健康指数λ。考虑到这3项重要性有所区别，根据以往经验，确定λh,λl和λs所占的权重依次为0.2，0.3和0.5。下面介绍λ的求解过程:当λh,λl和λs均为1时，则认为伺服机构健康状态良好，故认为λ为1；若这3项的值均大于0.7且不全为1，则取λ为这3项的加权和；当三者中有值小于0.7但大于0，则加权后最小值所对应的λi即为λ的取值；若3者任一项为0，则λ取值为0。λ的表达式为

(7)

3 基于证据融合的健康评估模型

3.1 D-S证据理论

证据理论由DEMPSTER[7]提出，经SHAFER发展[8]之后，在信息融合、决策分析和目标识别等领域有着广泛的应用[9-11]。

证据理论的核心是证据合成方法。设焦元分别为B1,…,Bk和C1,…,Cr，则证据理论的基本合成算式为

(8)

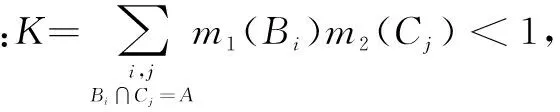
3.2 对证据理论的改进

合成规则具有简洁性和实用性，但当证据存在高度冲突时，融合后的结果通常和实际情况相违背[12]。因此，国内外很多学者对证据理论进行了大量的改进研究。本文结合前人的研究成果[13-15]，从修正证据源和改进合成算式两方面出发，对证据理论进行改进，使之更好地处理冲突。

在修正证据源方面，本文引入一种广义Jaccard系数[16]来描述证据体之间的相似度。

定义1存在两个n维向量X和Y，则这两个向量之间的相似程度可用广义Jaccard系数来描述,即

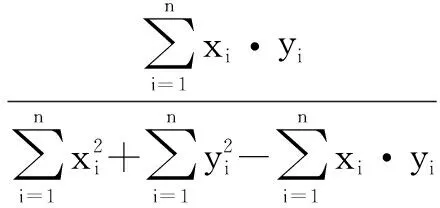
(9)

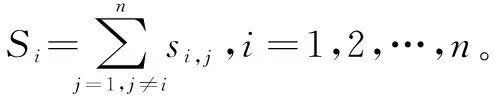
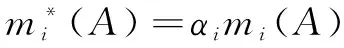
(10)

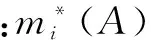
在冲突处理方面，本文方法引入了局部分配冲突的思想[15]，表达式可以概括为

(11)

式中,c(A)表示局部冲突中分配给焦元A的冲突部分。利用得到的修正BPA函数进行合成，得到的合成算式为

(12)

式中：m为对应的BPA值；c(A)为局部冲突中分配给焦元A的冲突部分。经验证，此方法仍然满足D-S合成算式的良好性质。

3.3 基于证据融合的多指标评估模型

伺服机构结构比较复杂，测试参数较多，各项参数的优劣判别具有一定模糊性和不确定性。因此，本文采用证据理论的方法对伺服机构健康状态进行评估。其基本思想为：将第1章中的各项指标作为评估因素集，进行归一量化后，利用模糊隶属度函数转化为表征状态的BPA值，再由D-S理论进行数据融合，最终实现对伺服机构的健康状态评估。基于证据理论的伺服机构健康状态评估模型如图3所示。

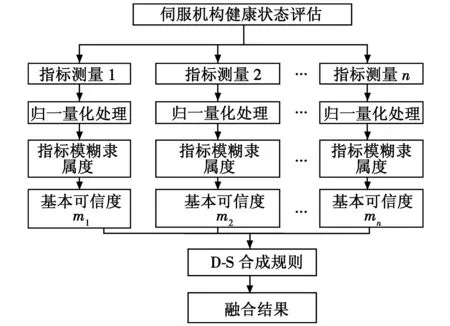
图3 伺服机构健康状态评估模型Fig.3 Servo mechanism health assessment model

已知证据理论合成算式满足结合律和交换律，为计算方便，首先按照合成算式将静态测试项目和动态测试项目下的指标BPA值分别进行融合，得到静态和动态测试的BPA值，便于判别影响伺服机构健康状态的项目，而后，再进行一次融合得到伺服机构的健康状态。

4 实例分析

本文以某伺服机构为例，对其健康状态进行分析。该伺服机构自2010年开始，截止2015年获得最新的测试数据已经工作6 a。以该伺服机构的静态参数相关的4个关键参数为例进行评估研究，得到其2015年的测试数据如表1所示。

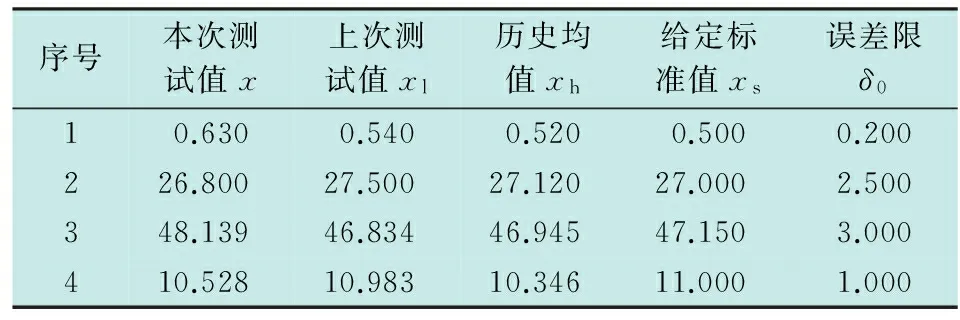
表1 静态特性各项测试数据

首先利用第2章的方法对上述数据进行归一量化处理得到处理后的数据如表2所示。

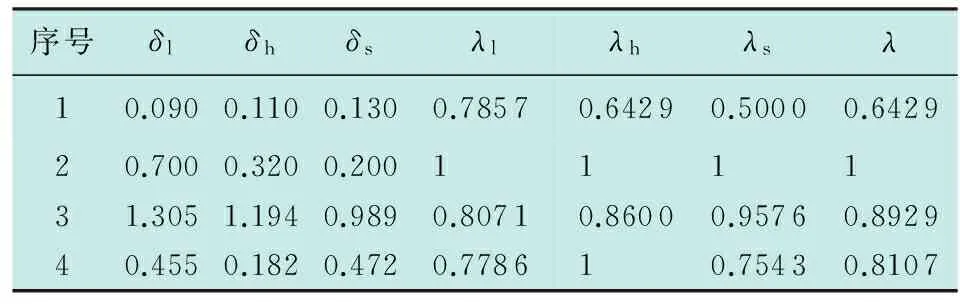
表2 静态特性数据归一量化表

根据归一量化后的数据，由状态隶属度函数计算可得各项参数的隶属度，结果如表3所示。

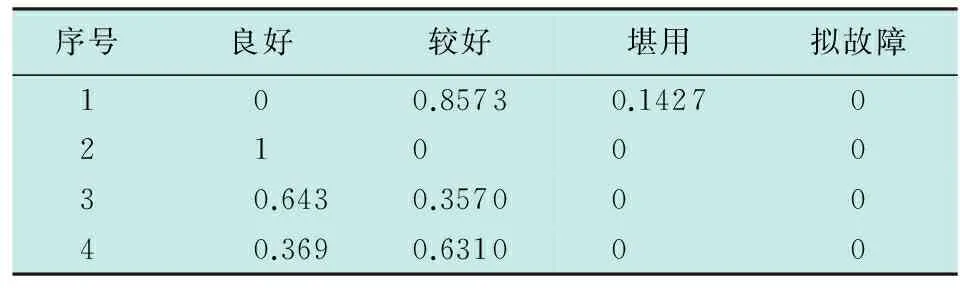
表3 测试数据隶属度

利用第3章权重系数算式计算各项参数修正后的隶属度，结果如表4所示。

表4 修正后的隶属度

合成后得到的静态特性在识别框架下的BPA值为β1=(0.500 9,0.489 6,0.000 3,0,0.009 2)。

对动态特性各项指标进行融合得到动态特性BPA值为β2=(0.304 8,0.584 9,0.1,0,0.010 3)。再次融合后得到伺服机构健康状态BPA值为β=(0.394 7,0.587 2,0.017 5,0,0.000 6)。最终结果的不确定度为0.000 6，健康状态等级为较好。对该伺服机构2010～2015年的健康状态进行评估，分别为良好、良好、良好、良好、较好、较好。鉴于该伺服机构的状态是逐步退化的，因此认为本文提出的方法是可行的。同时，由静态特性和动态特性的BPA值可知，动态特性退化较静态特性严重。

5 结论

对伺服机构进行状态评估，需要考虑多种指标，本文从静态特性和动态特性两个方面出发，将其状态分为良好、较好、堪用以及拟故障，并在此基础上提出一种基于改进证据理论的健康状态评估方法。

本文运用改进证据理论的融合方法，结合伺服机构的各类测试数据，对其健康状态进行实时评估，有效改进了以往“非此即彼”的评价模式，对装备测试评估方法的改进具有重要的借鉴意义。

[1] WANG J J,NIE R R,ZHANG H Y,et al.Intuitionistic fuzzy multi-criteria decision-making method based on evidential reasoning[J].Applied Soft Computing,2013,13(4):1823-1831.

[2] JIN G,MATTHEWS D E,ZHOU Z B.A Bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries in spacecraft[J].Reliability Engineering and System Safety,2013,113(1):7-20.

[3] WICKRAMARATHNE T L,PREMARATNE K,MURTHI M N.Monte-Carlo approximations for dempster-shafer be-lief theoretic algorithm[C]//Proceedings of the 14th In-ternational Conference on Information Fusion,IEEE,2011: 461-468.

[4] 朱忠惠.推力矢量控制伺服系统[M].北京：宇航出版社,1995.

[5] 崔吉俊.火箭导弹测试技术[M].北京:国防工业出版社,1999.

[6] 丛林虎,徐廷学,董琪,等.基于改进证据理论的导弹状态评价方法[J].科技导报,2013,31(30):15-18.

[7] ARTHUR P D.Upper and lower probabilities induced by a multi-valued mapping[J].Annals Math Statist,1967, 38(2):325-339.

[8] GLENN S.Mathematical theory of evidence [M].Princeton:Princeton University Press,1976.

[9] 权文,王晓丹,史朝辉,等.多源不确定性信息融合中的冲突证据快速合成方法[J].系统工程与电子技术,2012,34(2):333-336.

[10] 胡昌华,司小胜,史小华.基于ER的陀螺漂移组合预测模型[J].控制与决策,2009,24(2):202-205.

[11] 李鹏,刘思峰.基于灰色关联分析和D-S证据理论的区间直觉模糊决策方法[J].自动化学报,2011,37(8)：993-998.

[12] ZADEH L A.Review of a mathematical theory of evidence[J].AI Magazine,1984,5(3):81-83.

[13] 周哲,徐晓滨,文成林,等.冲突证据融合的优化方法[J].自动化学报,2012,38(6):976-985.

[14] 张燕君,龙呈,李达.基于冲突表示的冲突证据融合方法[J].模式识别与人工智能,2013,26(9):853-858.

[15] 郭华伟,施文康,刘清坤,等.一种新的证据组合规则[J].上海交通大学学报,2006,40(11):1895-1900.

[16] 潘磊,雷钰丽,王崇骏,等.基于权重的Jaccard相似度度量的实体识别方法[J].北京交通大学学报,2009,33(6):141-143.

OnHealthEvaluationMethodforaCertainServoMechanism

ZHANG Xiao-yu, HE Hua-feng, ZHENG Jian-fei, DONG Hai-di

(Rocket Force University of Engineering,Xi’an 710025,China)

Different solutions of maintenance and operation should be taken for equipment at different health levels.The current testing and evaluation of equipment is still realized by the “true or false” method,which can only describe whether the equipment is normal or not,and the health level can’t be evaluated.Aiming at this problem,a health status assessment method based on improved evidence theory is proposed,taking a certain type of servo mechanism as the research object.Firstly,a set of parameters is proposed to represent the health of the servo mechanism comprehensively,and a normalization method is used to process the test data.Furthermore,the membership of each processed parameter is fused based on the improved evidence theory,and thus the health status level of the servo mechanism is obtained.Finally,the proposed method is verified by the case study to a certain servo mechanism.It is demonstrated that the proposed method is valid,with certain application value.

servo mechanism; weaponry; health evaluation; test data; improved evidence theory

O213.2

A

1671-637X(2017)03-0064-04

2016-03-24

2016-04-24

国家杰出青年基金(61025014)；国家自然科学基金(6117 4030)

张晓雨(1991 —),男，河北衡水人，硕士生，研究方向为装备健康管理。