助航灯光系统中恒流调光器的研究*

甘雪，曹太强，刘中豪，林玉婷

（西华大学电气与电子信息学院成都610039）

0 引 言

恒流调光器是机场助航灯光系统调节不同光亮度的重要设备，研制一种高性能、低成本的恒流调光器对目前的机场系统来说非常重要。目前大部分机场采用交-直-交电路系统作为助航灯光恒流调光器的拓扑电路［1-5］，恒流调光器的主电路拓扑如图1所示。恒流调光器采用三相交流供电，在电网端采用二极管整流，前端AC-DC-AC电路主要起变频作用，后端AC-DC-DC电路可得到稳定的直流输出。文中采用逆变器的直-直变换器模式，在负载端直接得到恒定的直流输出电流，省略逆变器后端AC-DC-DC电路，降低了系统电路的经济成本。在传统的电压电流双环控制的基础上［2-5］，采用瞬时无功功率理论［6-8］。采样负载的电压和电流经单相变换三相处理后经abc-αβ，αβ-dq变换，把 d轴分量和q轴分量进行了合成，得到了指令电压和指令电流，控制指令电压和指令电流和参考值的误差经开关管作用后能得到纹波较低的输出电流和交流侧的谐波含量较低电流。通过状态解的分析，设置合理的LC参数［9-10］是保证系统稳定的关键。相比传统的双环控制［11-12］，它能够进一步减少输出电压电流纹波。最后通过仿真，验证了上述论述的正确性。

图1 恒流调光器的主电路拓扑结构Fig.1 Main circuit topology of constant current dimmer

1 新型恒流调光器分析

1.1 新型恒流调光器模式分析

采用逆变器运行在直-直变换器模式，使前端AC-DC-AC电路的输出为恒定的直流；在这种模式下，不仅可以得到稳定的直流输出，还可以节省传统恒流调光器后端不可控整流和DC-DC部分。为方便分析，设恒流调光器的前端为一个恒定电源（经ACDC变换之后），单相桥式逆变器如图2所示。

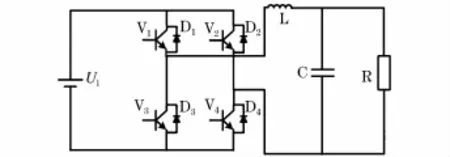
图2 单相桥式逆变拓扑Fig.2 Single-phase bridge inverter topology

按照传统的导通过程，开关管 V1、V4与V2、V3时序上互补，而二极管D1和D4一直都没有电流流通，所以直-直模式下具体导通过程如图3所示。

过程1：开关管V1、V4开通，电路给负载R供电，电感L、电容C充电，是电源供电过程。

过程 2：开关管 V1（V4）和二极管 D1（D4）导通，电感L放电，是续流过程。

过程3：开关管V2、V3开通，该过程相对特殊，一方面电源给电容C充电，一方面电容C向负载放电，起续流作用。

这三种情况下的基尔霍夫电流方程也有所不同，如图4所示，过程1和过程2虽然是两个不同的过程，但是过程2的导通发生在过程1的后半段导通里。

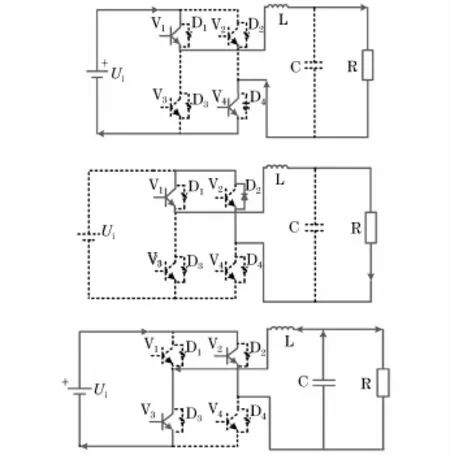
图3 逆变桥的导通过程Fig.3 Conduction process of the inverter bridge

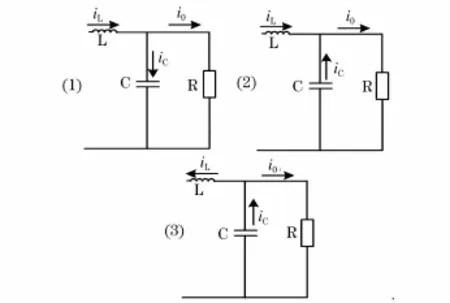
图4 三种模式下电流的变化情况Fig.4 Changes of current in three modes

过程1中电容电感都充电，前半段的基尔霍夫电流方程为：

其中iL增大，i0和iC同时增大，当i0达到稳定时，二极管开始续流，V1和V4的导通仍在继续，但流过的电流在减小，这时过程2的基尔霍夫方程为：

其中i0不变，iL减小，iC增大，到过程3时，电流方程为：

其中iL增大，iC增大，i0不变。

1.2 电路的状态解及其分析

采用状态空间模型对上述几个导通过程进行描述，根据三个过程列写出它们的状态空间方程为：

上式是对恒流调光器DC-AC部分为直-直变换器时的数学描述，对于负载端部分的二阶系统，合理的选择电感和电容参数将决定输出电流的纹波系数。设占空比 d＝ton/T，m＝δon/ton，（占空比 d和 m都是在平均状态下的占空比），代入式（4）～式（6）中，整理得：

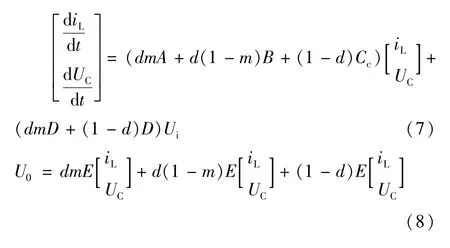
对式（7）、式（8）进行变形，整理得：

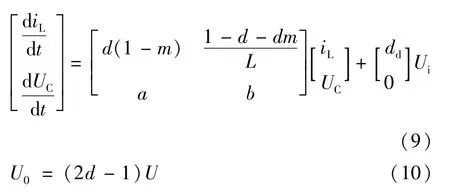
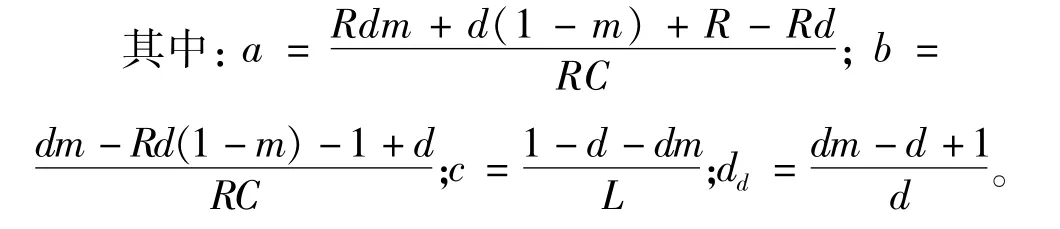
求出电路输出电流的解如式（11）所示，该解在恒定电压的输入下（阶跃输入）是一个带直流偏置的具有三角函特征数解，可以表示为：i0＝A＋m cos（ωt＋θ），其中m≪1。根据输出方程U0＝（2d－1）UC，要使输出值具有直-直变换器的特性，U0必为正，则占空比d必须大于0.5，即2组开关的占空比不等。

其中：α＝（dm－d＋1）；β＝（dm－Rd（1－m）－1＋d）；γ＝（Rdm＋d（1－m）＋R－Rd）（1－d－dm）。

由线性控制理论知能控的判据为：

由上述条件得：

显然要使它的秩为1必须使R（dm＋1－d）＝0，由于d、m都是小于1的数，所以R（dm＋1－d）＞0，所以系统完全能控。系统的能观性秩判据为：

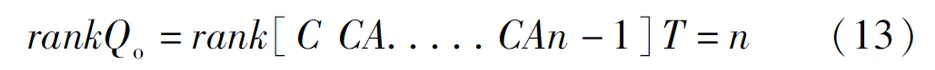
由式（13）可得：

当（1-d-dm）（2d-1）/L中 d＝0.5时有矩阵的秩n＝1，所以为了保证完全能观，d不能为0.5。在后面的仿真中，d大约为0.8～0.9。同样判断其稳定性，根据稳定的条件：Re{λi（A）}＜0。

2 控制方法分析

采用基本的电压电流双环控制，在PI调节基础之上，加入瞬时无功功率理论的方法，对输出的电压和电流进行坐标变换c之后再进行合成，其控制原理图如图5所示。

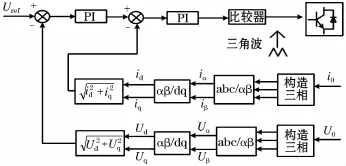
图5 基于瞬时无功功率理论的电压电流双环控制Fig.5 Voltage and current double loop control based on instantaneous reactive power theory

设输出电流i0和输出电压U0为X0＝A＋m cos（ωt＋θ），经过单相变换到三相之后有：

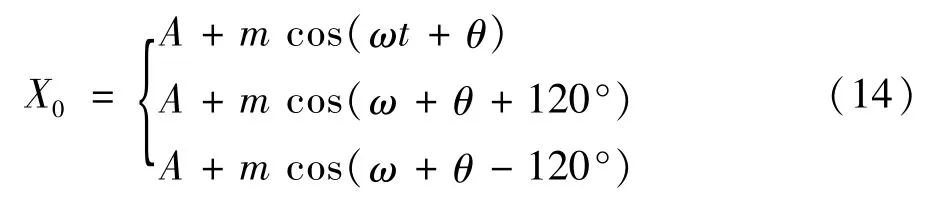
瞬时无功功率理论是由赤木提出的有关瞬时无功功率的定义，在坐标变换中不考虑电压和电流的零序分量，将它们变换到正交的坐标α-β上，由三相坐标abc变换到两相坐标系α-β的表达式为：

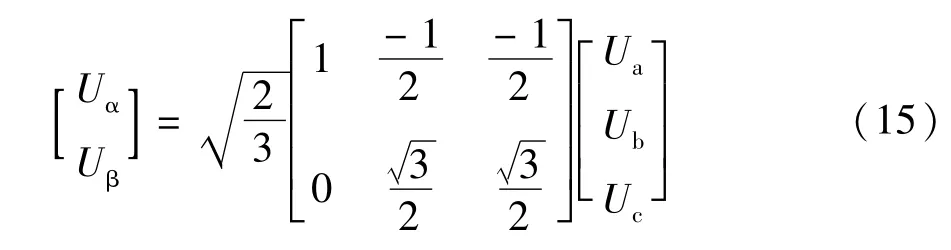
经坐标变换后有：

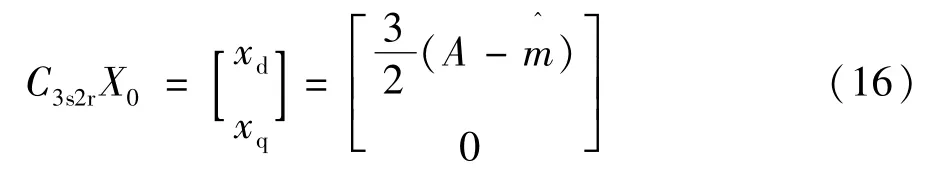
由式（16）可知，与X0＝A＋m cos（ωt＋θ）相比，输出值的纹波进一步减少，将扰动项减少到只有m。根据自动控制原理，进一步设计控制回路的补偿网络，通常采用PI调节器，PI调节器的时域表达式为：

其中Kp加大，系统的响应速度加快，稳态误差减少，从而提高控制精度，但过大的比例系数，会使系统产生超调，并发生振荡；增大积分时间常数，有利于减少超调量，减少振荡，使系统稳定，同时延长系统消除静态误差的时间。电压电流双环中，电压外环是对电路输出值的调节作用，内环是精调的作用。根据波特图中系统的低频段、中频段和高频段的要求进行设计。

3 仿真分析

在MATLAB中进行仿真，其中电路参数 L＝0.005 084 H，C＝0.005 F，负载为R＝1Ω，在AC-DC滤波电抗Lf＝0.37 H。在负载端采样输出波形后，设置一个波周期的T/3和2T/3的延时，从而得到从单相变到三相的输出。图6为开关管输出电流波形。

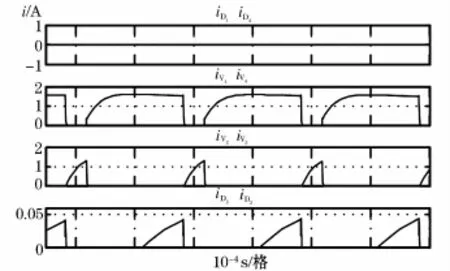
图6 开关管的输出电流Fig.6 Output current of switch tube

从图6中可以看到两个续流管D1和D4没有电流流过，只有D2和D3有续流作用，V1V4和V2V3的导通情况不一样，这也是能够输出直流的原因。四个开关管中V1V4和V2V3在时序上互补，在整个导通过程中，V1V4的导通占主导地位，占空比较大，可通过调节占空比来调节输出电流的幅值。两组开关管中，V1和V4占主要电流的输出部分，这符合前述的系统直-直变换器的要求，即d＞0.5。为了保证完全能控，d的值将达到0.8～0.9左右，仿真波形验证了该理论的正确性。因为前端不可控整流输入馒头波，输出电流波形有一个上升下降的过程。每个周期中，电流从零逐渐增大到稳定状态，由于电感的存在，电流不能突变，续流二极管续流，直到下一个周期。负载端输出的电压和电流如图7所示。

从图7中可以看出输出电压和电流很快达到稳定状态，输出电流（局部放大）波形的纹波仅为1%。在新型恒流调光器中，采用基于瞬时功率理论的电压电流双环控制策略，电路响应速度快，超调量小，约为1.024 8 A。由图8和图9可知，在前端整流电路加入滤波电抗后，网侧电流畸变小，交流侧输入电流趋于正弦化，且THD值也为2.7%，符合控制要求。

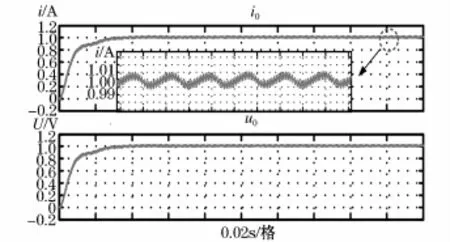
图7 负载端输出的电压和电流Fig.7 Load side of the output voltage and current

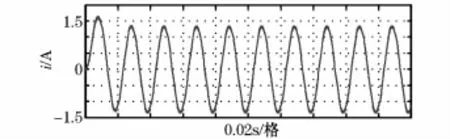
图8 交流侧的输入电流Fig.8 AC side of the input current

图9 交流侧输入电压的THD值Fig.9 THD value of the AC side input voltage

4 结束语

采用逆变电路的直-直变换器模式得到恒定的直流电流，相比传统的助航灯光系统可以节省后端ACDC-DC电路的经济成本。在传统电压电流双环控制的基础上，使用瞬时无功功率理论，将dq轴的电压电流分量合成指令电流，它的输出解相比传统的输出少了cos（ωt＋θ）这个扰动量，降低了其输出电压的纹波。仿真结果显示该方法使电压纹波从2%降到1%并且可以得到稳定的输出电压和电流。系统响应速度快，仅为0.03 s，超调量小，在交流侧端的输入电流趋于正弦化，THD值仅为2.7%，验证了新型恒流调光器的正确性和控制方法的可行性。