基于自适应小波阈值去噪和HT-LMD的电能质量扰动检测方法*

唐圣学，付滔，李志刚

（河北工业大学电气工程学院，天津300130）

0 引 言

现代电力系统中，随着电力电子设备等非线性负载的广泛使用，导致电能质量污染越来越严重［1］。各种电能质量扰动严重影响着各种用电设备，甚至是电网的安全可靠运行，因而必须采取措施来治理和改善。

扰动检测是治理和改善电能质量的前提，是研究的热点。目前，电能质量扰动检测方法主要有小波变换［2-3］、S变换［4］、数学形态学［5］、分形理论［6-7］、时频原子算法［8］和希尔伯特变换等［9］。

虽然这些方法在电能质量扰动检测领域都取得了较好的检测结果，但也存在各自的不足。小波变换的检测效果取决于基函数的选择和分解尺度，无法保证最优的分解效果，而且对于低频扰动不能很好定位；S变换得到的S矩阵含有大量冗余信息，会干扰甚至掩盖扰动特征，影响识别准确性；时频原子算法无法精确地检测出小于2个周波的瞬时电压暂降（暂升）的特征参数［10］。

希尔伯特变换（HHT）先用经验模态分解（Empirical Mode Decomposition，EMD）将复杂信号分解为若干固有模态函数（Intrinsic Mode Function，IMF）分量之和，然后用希尔伯特变换（Hilbert Transform，HT）求取每个IMF的频率和幅值，根据频率突变点定位扰动时刻，该方法有很好的自适应，克服了小波变换、S变换等时频分析方法的局限性。但是，也存在一些不足，如端部失真，模态混叠，出现虚假分量等问题［11］。

LMD的端点效应相比EMD在程度上轻得多，端点效应作用范围也比较小［12］。但在干扰定位方面容易造成信号奇异性特性丢失，文献［13］提出的HTLMD算法结合了LMD算法优点，通过对分解信号作希尔伯特变换（HT），提高了信号检测定位能力。

文章在文献［14］基础上进一步采用改进乘积函数PF终止判据，提出基于正交性（Orthogonality Criterion，OC）的HT-ILMD检测方法，突出了分解的物理意义，且减少了迭代次数，提高了检测速度，缩短了检测分析所需的时间。针对实际信号中往往夹杂着许多噪音信号，采用自适应小波去噪技术对噪声信号进行预处理，减少了噪声对分解效果的影响，有效的抑制了LMD对噪声信号敏感的缺陷，提高了含噪信号的检测精度。

1 HT-LMD电能质量扰动检测方法

1.1 LMD分解

本质上，LMD根据信号固有的包络特征通过迭代算法自适应地从原始信号按频率递减的顺序逐级分离出纯调频信号和包络信号，包络信号和调频信号之积为具有瞬时频率意义的PF分量，即原始信号的时频分布。对于信号 x（t），分解过程，如图 1所示［15］。

分解算法迭代终止的条件为：

实际应用中，为避免过多分解次数，通常设一个变动量 δ，可令1－δ≤ain（t）≤1＋δ时，迭代终止。

图1 LMD分解流程Fig.1 LMD decomposition process

PF1包含了原始信号中最高的频率成分，是一个单分量的调幅-调频信号，其瞬时幅值就是包络信a1（t），其瞬时频率 f1（t）由纯调频信号 S1n（t）求出，即：

通过上述LMD分解，原始信号 x（t）可由 uk（t）和所有PF分量重构，即：

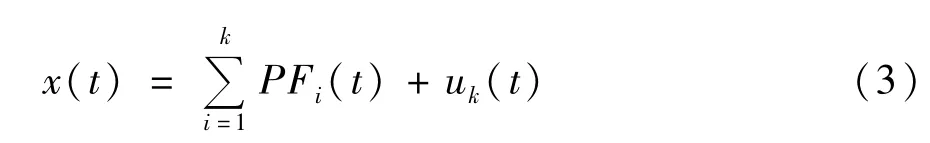
原始信号x（t）完整的时频分布由所有分量PF的瞬时频率和瞬时幅值表征。

1.2 HT-LMD电能质量扰动检测方法

文献［13］比较了HHT和LMD方法在电能质量扰动检测中的优缺点，指出LMD方法在整个波形中波动幅度、端点效应、迭代次数都优于HHT方法，但是定位能力明显不及HHT方法。为了提高LMD对突变信号的定位能力，文献［13］提出对LMD每个分量PF进行HT变换后再采用HT变换的瞬时频率函数来提高定位能力ILMD方法（文献［13］称为改进的LMD方法，为了区别文中称之为HT-LMD方法），即对原始信号x（t）分解得到的每个分量PF作HT变换，可得：

相应的解析信号表达式为：

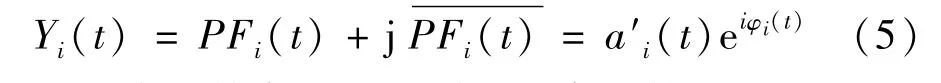
对相位函数求导可得瞬时频率函数为：

对比LMD和HT-LMD可见，LMD方法采用式（2）纯调频函数获取瞬时频率，纯调频函数为余弦函数，需要对S1n（t）超出－1与＋1部分进行置1或－1处理。这样处理导致了瞬时频率曲线扰动起止时刻与其临近时刻幅值无明显突变点，因而无法进行精确定位。HT-LMD方法瞬时频率计算，反正切函数不受函数极值限制，因此瞬时频率曲线可完整保留扰动起止时刻所产生的突变信息。

1.3 噪声对HT-LMD电能质量扰动检测的影响

扰动信号通常含有噪声，文献［13］没有考虑噪声对HT-LMD的影响。下面文中以多谐波信号为例说明噪声对LMD分解效果的影响。谐波信号X（t）为：

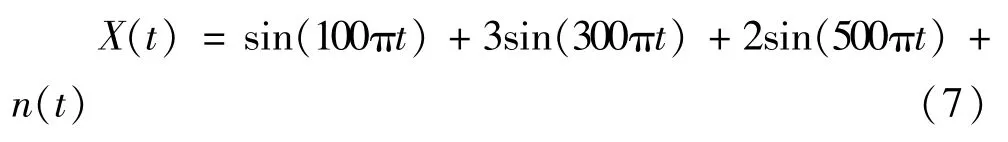
式中n（t）为高斯白噪声。

图2 无噪信号x（t）LMD分解Fig.2 Signal without noise decomposition by LMD

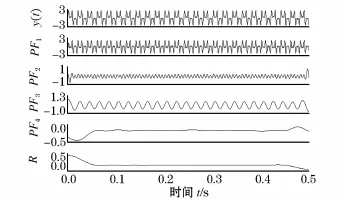
图3 含噪信号y（t）的LMD分解Fig.3 Signal with noise decomposition by LMD

图2给出了无噪声谐波信号及其LMD分解后的PF分量波形图，其中分量PF1、PF2和PF3分别对应于250 Hz、150 Hz和50 Hz频率成分的谐波信号，说明LMD在信号无噪声时能有效分解出信号分量。图3给出了含噪声信号及其LMD分解后的PF分量波形图。由图3可见，分解结果比实际所含信号频率成分多出了一个分量PF4，且出现局部失真，因此噪声严重影响了LMD分解的有效性。

为了减少噪声对HT-LMD分解效果的影响，文中提出小波自适应阈值滤波和正交性判据（OC）相结合的改进HT-LMD的电能质量扰动检测方法。

2 改进的HT-LMD方法

2.1 自适应阈值小波去噪方法

电能质量扰动检测所采集的信号中，有用信号通常表现为低频信号，噪声干扰表现为高频信号。此外，需要在滤除噪声的同时尽量保留原有信号的奇异性特征。因此，文中采用小波自适应阈值滤波技术滤除电能质量信号中的噪声。具体原理如下：

设含噪信号为：

式中 y（t）表示含噪信号；x（t）表示有用信号；n（t）表示噪声信号。小波去噪过程可描述为：

式中 W（·），W－1（·）分别为小波分解和重构运算，通常采用Mallet快速算法实现；u为含噪声信号的小波系数；th为阈值；D（·）为去噪运算；~u为经过采用阈值th和去噪运算D（·）处理后的重构小波系数；x^为重构后的去噪信号。由式（9）可见，小波去噪核心工作是非线性运算D（·）操作，去噪效果好坏的关键是选择合适的阈值函数与最佳阈值。

目前，硬阈值和软阈值是常见的两种阈值函数。硬阈值函数因在阈值处函数不连续，容易造成缺乏像原始信号的光滑性；软阈值函数虽连续性较好，但存在恒定的偏差。为了尽可能去除噪声和保留信号原有的奇异性，文中采用一种自适应阈值函数和最佳阈值对电能质量原始信号去噪。选用的自适应阈值函数为：

式中th为阈值；m为可调参数，可取大于1的连续实数。m决定了函数η（·）形状、性质。当m接近于1时，类似于软阈值函数；当m＞10时，类似于硬阈值函数。

采用小波阈值去噪时，在高频部分噪声所占比重大，宜采用偏硬阈值函数去噪；低频部分所占比例小，宜采用偏软阈值函数去噪。根据这一特点可知，通过调整m可为不同尺度下的小波分解信号选择合适的阈值函数。此外，为了获取更好的去噪效果，自适应去噪还要为不同尺度下的分解信号自适应确定阈值th。下面给出一种根据信号统计特性的自适应函数参数m和阈值th的确定方法。

函数参数m自适应确定原理为：先计算各尺度下噪声能量大小和各层总能量，然后根据式（11）计算：

阈值th自适应确定可采用SURE估计得到，具体计算方法为：设a为小波分解的低频信号，定义：

根据 SURE无偏估计理论［15］和式（10），最小均方误差意义下的自适应阈值满足：

通过求极小值可获得对应尺度的最优阈值th。

2.2 正交性判据迭代终止

由1.1节LMD分解可知，包络估计函数终止迭代条件是理想的，但工程中无法实现，故简化为采用变动量δ：即落入1－δ≤a1n（t）≤1＋δ终止结束。实际分解中，变动量δ只能依据经验值确定；当信号中含有噪声时，变动量δ更难确定，不合理选定还会导致迭代次数增加，增加计算量。

根据LMD分解分量正交性特点，文中将EMD分解终止正交性判据（Orthogonality Criterion，OC）引入到HT-LMD算法中，以降低噪声影响和减少迭代计算量。正交性判据OC定义为：

式中 x（k）是待分解信号；mij（k）为第 i个 PF分量时的第j次局部均值函数。理论上OC＝1时，迭代终止。实际应用中，常采用 mij（k）＝b·x（t），b反映了 mij（k）在 x（k）中的比例，可选最大幅值的比值、能量的比值等），于是 OC＝1/（1-b）。考虑噪声的影响，一般取 OC≤1.01，另外结合 max（｜mij（k）｜）≤0.001迭代终止条件，即可替代迭代条件。该判据充分保证了分解的正交性，且稳定性好、收敛速度快。

3 基于改进HT-LMD电能质量扰动检测方法

3.1 检测原理

文中提出的基于改进HT-LMD电能质量扰动检测方法如图4所示，具体过程为：先对含噪声电能质量信号进行自适应滤波去噪处理，进而对滤波后信号进行基于OC判据的HT-LMD分解获取PF分量，最后根据PF分量幅值特征、瞬时频率特征以及边际谱等特征进行比较分析，发现电能质量中的干扰信号。

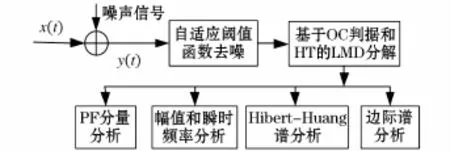
图4 电能质量检测过程Fig.4 Process of power quality detection

首先，针对式（7）给出的含噪声的多谐波信号，经过自适应去噪的HT-LMD分解后波形如图5所示。对比图5、图2和图3可知，经过自适应去噪的HTLMD分解，不存在多出的分量，局部失真也减轻了，跟无噪声信号分解的效果很接近，说明此方法是有效的。

表1给出了针对式（7）含噪声的多谐波信号采用LMD分解迭代终止准则和本文改进的正交性判据准则迭代次数和相应的OC值。

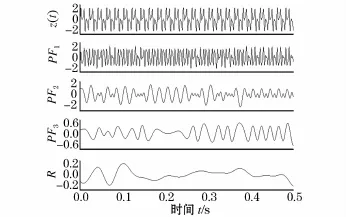
图5 多谐波去噪信号的分解Fig.5 Multi-harmonic de-noising signal decomposition

根据正交判据作为终止条件得到各PF分量的总迭代次数不过4次，而采用HT-LMD得到的总迭代次数为26次，相比采用OC判据不仅仅提高了各PF分量正交性，计算效率也明显高于HT-LMD。

表1 各PF迭代次数及OC值Tab.1 The PF iterations and OC values

3.2 单暂态检测分析

为了进一步说明文中的改进HT-LMD方法在电能质量扰动检测及定位的有效性，下面选取两种单暂态扰动信号、一种多暂态扰动信号和实测信号进行分析，信号采样频率为fs＝1 kHz，其信号处理工作在MATLAB环境下进行，采用db4为小波分析小波。

3.2.1 电压暂升

假设两种单暂态扰动信号发生时间为t1＝0.15 s，终止时间t2＝0.15 s。第一种单暂态扰动信号为电压暂升扰动，其数学表达式为：

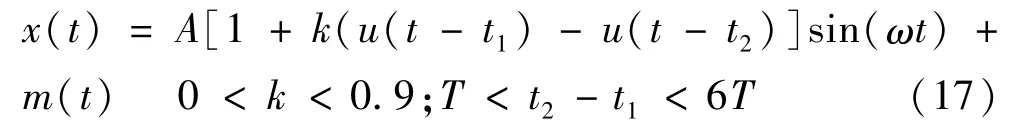
式中 k＝0.6；τ＝0.0125；m（t）为高斯白噪声（以下同）。

图6给出了电压暂升扰动波形图，其中图6（a）为无噪声信号HT-LMD分解波形图，图6（b）为含噪声信号HT-LMD分解波形图和图6（c）为去噪的分解波形图。

由图6（b）可见，对含噪声的电压暂升扰动直接进行LMD分解，分解结果有5个分量PF1～PF5，比无噪声的分解结果多一个PF5分量，说明分解受到了噪声严重影响。而采用文中的HT-LMD分解的结果跟无噪声分解结果基本上一致，见图6（c），说明该方法可以有效去除噪声对LMD分解的干扰。

图6 电压暂升信号检测Fig.6 Voltage swell signal detection

根据图6（a）和图6（c）中 PF2分量极值，可定位暂升扰动的发生时刻和结束时刻，而图6（c）中PF2分量无法进行扰动定位，即此方法定位精度高。

3.2.2 暂态振荡

第二种单暂态扰动信号为电压暂升扰动，其暂态振荡信号的数学表达式为：

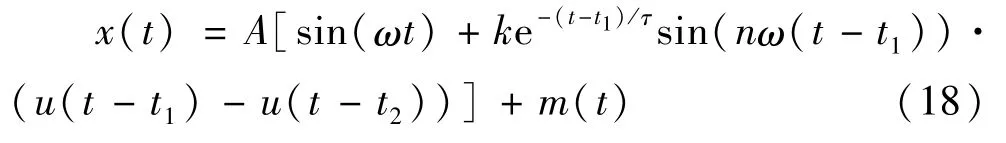
图7给出了暂态振荡信号及其边际谱，其中图7（a）为无噪信号和含噪信号波形，图7（b）为分量PF1的边际谱。由图7（b）可见，含噪信号PF1分量所含频谱范围宽，除噪后信号频谱宽度减小。为了说明文中LMD算法的扰动检测定位性能，表2给出了HT-LMD与本文方法定位检测结果。可见，该方法明显优于未改进的HT-LMD。

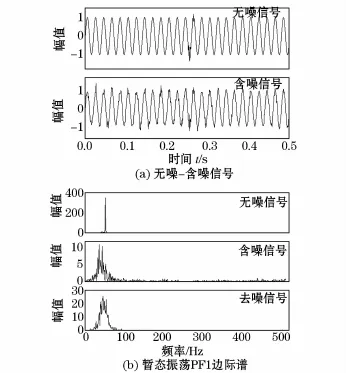
图7 暂态振荡信号检测Fig.7 Transient oscillation signal detection

3.3 多暂态检测分析

多暂态扰动信号为电压闪变，振荡起止时间分别为0.250 s和0.270 s。电压闪变信号的数学表达式为：

式中 k＝0.15；n＝0.5。

图8给出了电压闪变波形及PF1分量。由图8可见，含噪声信号的分解PF1分量出现局部失真，经过降噪后失真明显减小，扰动定位结果见表2。

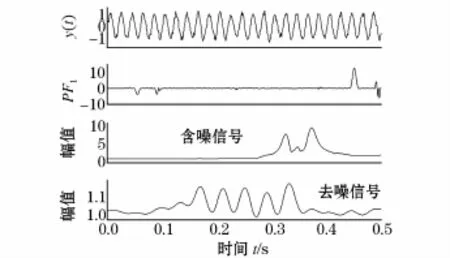
图8 电压闪变波形Fig.8 Voltage flicker waveform

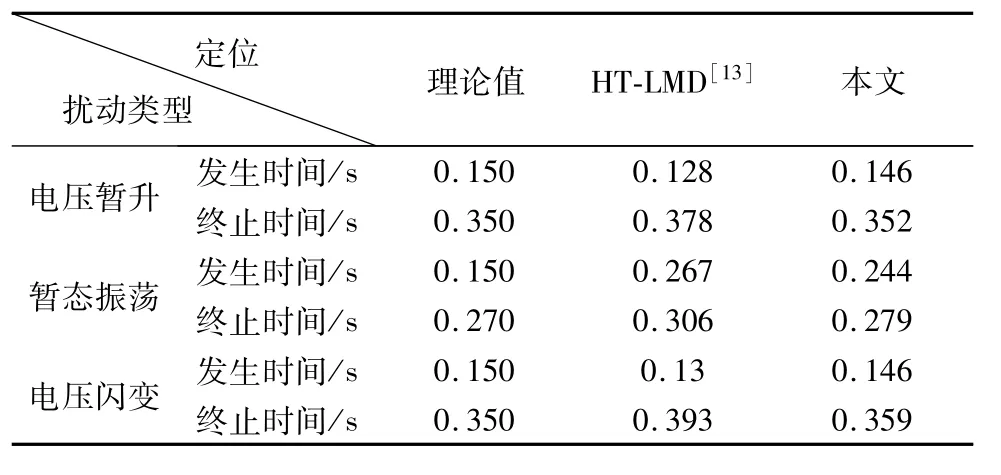
表2 扰动检测定位结果Tab.2 Location results of the disturbance detection

由表2可见，本文定位精度明显高于HT-LMD方法，说明本文方法能有效减弱噪音对HT-LMD方法的扰动定位的影响。

3.4 实测信号分析

为验证所提方法，以电容器组投切产生的电网电压暂降波形为例，电压暂降实测波形如图9所示，其中图9（a）给出了电压暂降实测波形图，图9（b）为电压暂降归一化的本文LMD分解图。由图9可见，此方法能有效的获取电压暂降LMD分量。

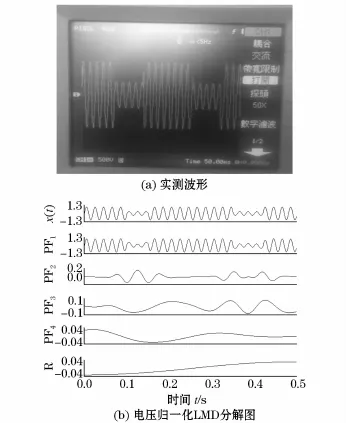
图9 电压暂降实测波形Fig.9 Voltage testing waveform

4 结束语

文中提出了一种新的HT-LMD的暂态电能质量扰动检测方法。该方法采用小波自适应去噪减弱噪声对检测效果的影响，采用正交性判据提高了分解效果和分解迭代次数。通过对典型模拟暂态电能质量扰动信和实测信号的检测表明，所提HT-LMD方法能有效减弱对提取信号PF分量的影响，能有效提高扰动定位效果。

需要指出的是：HT-LMD是近年来提出的一种类似于HHT分解方法，存在模态混叠和平滑跨度选取等问题；此外，正交性判据虽对加性白噪声具有良好的效果，对于其它类噪声需要进一步研究。