基于磁场测量的变压器绕组形变在线监测方法

周院超，王雪

（华北电力大学电力工程系，河北保定071003）

0 引 言

变压器在受到多次外部短路电动力的冲击后，其绕组可能会发生不可逆的形变［1］，这是造成变压器绕组匝间短路故障的首要原因［2-3］。因此，对变压器绕组形变进行准确、及时的监测，将有利于及早提出解决方案，防止故障扩大。对变压器绕组形变检测的传统方法，如频响法和低压脉冲法等［4-6］，属离线监测法。对于大容量变压器，离线监测法已难以保证其运行可靠性，迫切需要提出绕组形变的在线监测法。基于漏感或短路电抗的参数辨识法［2-3，6，10］理论上可用于变压器绕组形变的在线监测，但由于变压器漏感较小，参数辨识对计算精度要求极高，且易受到扰动较影响。汲盛昌［1］和马宏忠［8-9］等提出基于振动信号的绕组形变在线监测方法具有很好的应用前景，该法在建立变压器绕组形变程度与检测量间的对应关系方面仍需进一步研究。这些在线监测方法未能实现对变压器绕组形变的分类。文献［10］提出用磁场能量和漏感等参数对绕组形变的分类，其所用磁场能量难以在线获得而使该法难以投入实践应用。

基于漏感的变压器绕组形变监测法是以变压器磁场与绕组形状的密切相关为基础的，因此，有必要对变压器形变前后的磁场分布进行深入的研究。磁场计算的方法主要有数值法、解析法和实验法，有限元法作为数值法的一种，其计算精度高，对模型修改方便，且有很多成熟的仿真软件，如 ANSYS，Ansoft等，而被广泛用于对变压器的磁场进行分析，其对变压器磁场的分析的精度已多次被实际测量和理论分析所验证［10，12-13］。

文章用ANSYS建立变压器绕组形变前后的仿真模型，深入分析了变压器绕组形变与其磁场分布间的关系，并提出在变压器油隙的合适位置装设磁场传感器，通过测量变压器的磁场，实现对变压器绕组形变的在线监测。最后，对变压器绕组形变的判断方法并对磁场传感器安装位置进行了优化。

1 变压器的模型建立

1.1 变压器的电磁关系

变压器磁势平衡方程为：

按照罗氏［14］的定义，变压器一次侧电流可表示为励磁电流与负荷电流的和，即：

将式（2）代入式（1）得：

式中N1、N2分别为变压器一、二次侧绕组匝数；i1、i2分别为一、二次侧电流；i0为励磁电流；i1h为一次侧负荷电流分量；F0为主磁势。

式（4）所示的主磁势产生主磁场，主磁场主要分布在铁芯中，仅很少一部分泄露到油隙中，式（3）表示漏磁势，其产生的磁场主要分布在油隙和绕组区等非铁磁材料区。由于变压器正常运行时主磁场的泄露相对较小，可认为油隙中的磁场均由负荷电流产生，在建立变压器模型时，加载式（3）所示的和为零的磁势。

1.2 变压器的有限元模型

文中所用的变压器参数见表1。

表1 变压器参数Tab.1 Parameters of transformer

建模时做以下近似处理：

（1）忽略变压器绕组和铁芯外的部分；

（2）铁芯相对磁导率为额定磁导率；

（3）变压器结构对称，建立二维模型。

变压器绕组正常时的二维ANSYS模型如图1所示。

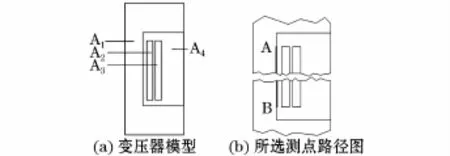
图1 变压器二维模型Fig.1 Transformers two-dimensional model

磁场传感器需要固定的基座，因此，只有特殊位置的磁场是可测的。文中按照以下原则选择测量点：

（1）测点位置可以方便安装磁场传感器；

（2）测点位置不随绕组的形变而改变；

（3）暂不考虑经济性，假设传感器密集地分布在满足上述原则的线段上。

依据上述原则，选择铁芯边缘与绕组等高的线段AB作为磁场传感器的安装路径，如图1（b）所示的线段AB，A为路径的起点。ANSYS后处理选择路径输出，输出点数为181个。

根据变压器绕组受力的理论分析及运行中情况统计结果［2，15］，变压器绕组常见的轴向形变有绕组的整体压缩形变、局部压缩形变和对称性压缩形变等三种类型，如图2所示，其中，图2（a）为低压绕组整体压缩形变，图2（b）为低压绕组局部压缩形变，图2（c）为低压绕组对称夸缩形变。

图2 常见的变压器轴向形变Fig.2 Common transformer axial deformation

根据形变发生的位置不同，将上述三种形变分为低压上端整体压缩（C1）、低压上端局部压缩（C2）、低压对称压缩（C3）、低压下端整体压缩（C4）、低压下端局部压缩（C5）、高压绕组上端整体压缩（C6）、高压绕组上端局部压缩（C7）、高压对称压缩（C8）、高压下端整体压缩（C9）、高压下端局部压缩（C10）共10种情况。

1.3 磁场传感器的选择

磁场测量的传感器有磁力法磁强计、磁感应法磁强计、磁通门磁强计、超导效应法磁强计、磁光效应磁强计、霍尔元件等［16］。

其中霍尔元件在低温和高温环境下均能有效工作，而且体积小、灵敏度高、线性度好，其最小精度能达到达1 Gs，因而非常适宜测量狭小空间处的磁感应强度。考虑到本研究传感器安装空间狭小、可能存在高温条件，因此，选择霍尔元件作为本研究的磁场传感器，文献［11］与文章的测量要求相当，其选用的也是霍尔元件。

2 仿真分析

磁场分布规律仅与绕组形状有关，与加载电流大小无关，在建立变压器绕组模型时，选择加载额定电流。

2.1 绕组正常时磁场的分布

绕组正常时磁感应强度沿所设路径的分布如图3所示。

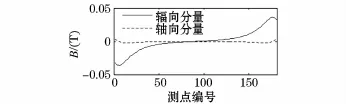
图3 绕组正常时的磁场分布Fig.3 Magnetic field distribution when winding is normal

由图3，沿路径磁感应强度的轴向分量几乎为0，且在所设路径中测量磁场轴向分量较为困难，因此，仅对路径磁场的辐向分量进行分析。

如图3，在路径中点处磁场的值为0，靠近端部，磁场的值较大，其最大值出现在路径端部附近，符合变压器磁场理论分布［14］。在路径中点两侧对称位置处，磁场呈现对称性。

2.2 绕组整体压缩形变时的磁场分布

分别建立变压器绕组各种整体压缩形变的模型，形变程度为5%，得到磁感应强度沿路径的分布如图4所示。

由图4（a），当低压绕组发生整体压缩形变时，形变发生在绕组上端时，上端磁场分布与正常时的差异明显大于下端，形变发生在绕组下端时，下端磁场分布与正常时的差异则明显大于上端。图4（b）所示高压绕组发生整体压缩形变与低压绕组发生整体压缩形变规律一致。

图4 绕组整体压缩形变路径上的磁场分布Fig.4 Magnetic field distribution when winding whole compression deformation

对比图4（a）与图4（b），当低压绕组上端发生形变时，上端磁场分布与绕组正常时相比，其变化量取负值，当高压绕组上端发生形变时，上端磁场分布与绕组正常时相比，其变化量取正值。形变发生在绕组下端，具有相同的规律，只是正负相反。

由图4（a）、图 4（b），路径中点处的磁场在绕组发生整体压缩形变时，其值与绕组正常相比，发生明显改变，磁场分布的对称性变差。

2.3 绕组局部压缩形变时磁场的分布

分别建立变压器各种局部压缩形变的模型，形变程度为5%时，磁感应强度沿路径分布如图5所示。

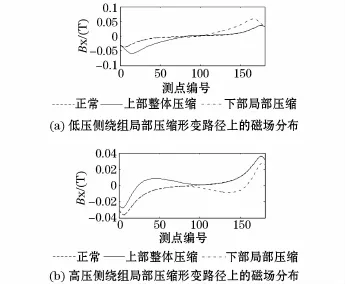
图5 绕组局部压缩形变路径上的磁场分布Fig.5 Magnetic field distribution as winding local compression deformation

由图5，当低压绕组发生局部压缩形变时，漏磁场的分布规律基本与变压器发生整体压缩形变基本一致，但在绕组未发生形变的部位，漏磁场在路径上的分布与正常时差异几乎为0，在路径中点处的磁感应强度值为0。

2.4 绕组对称压缩形变时磁场的分布

分别建立变压器对称压缩形变模型，形变程度为5%时，磁感应强度沿各路径分布如图6所示。

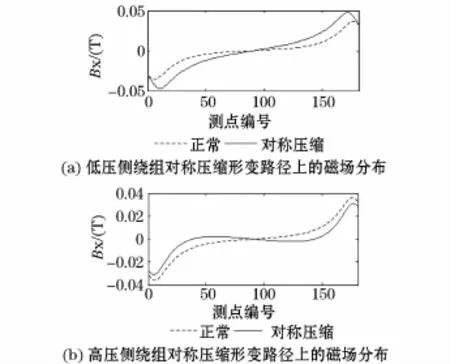
图6 绕组对称压缩形变路径上的磁场分布Fig.6 Magnetic field distribution as winding double side compression deformation

由图6，当变压器低压侧发生对称压缩形变时，其磁场变化规律与绕组整体压缩和局部压缩形变一致，但是，其磁场分布对称性未发生改变，路径中点处的磁场值为0。

2.5 绕组形变时磁场规律的定量分析

将路径分为上半区I和下半区II，为定量分析磁场随绕组形变的变化规律，定义以下五种数据指标：

（1）不对称度η＞ηmin

η是定量分析磁场沿路径的分布的对称性而定义的不对称度系数，即：

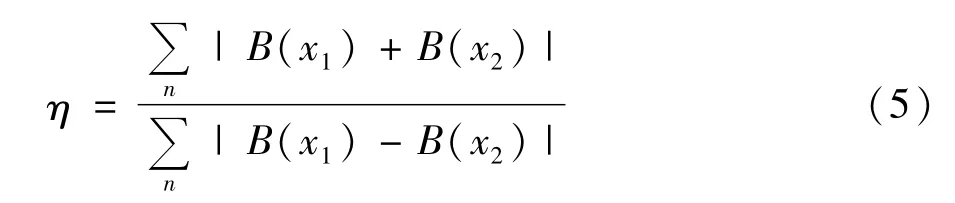
式中B表示路径上磁感应强度的辐向分量；x1、x2为关于路径中点对称的两点；n为区域I或II上的测点数。

由定义可知，不对称度为非负数，其值越大表明磁场的分布越不对称。绕组正常时，η＝4.409 3×10－5，表明在绕组正常时，磁场的对称性很好。

ηmin为考虑测量误差后对绕组正常时的不对称度的修正，如果该式满足，则判断结果为1，否则，判断结果为0；

（2）局部差异性大小∑｜△BIn｜＞∑｜△BIIn｜

其中I和II分别表示区域I和区域II；n为区域内测点编号；△BIn为区域I中测点n对应的磁场实测值与正常时的差值；△BIIn为区域II中测点n对应的磁场实测值与正常时的差值，如果该式成立，则判断结果为1，否则，判断结果为0；

（3）局部变化量正负∑△BIn＞ξ1

其中ξ1为传感器综合误差的绝对值，如果该式成立，则判断结果为1，否则，判断结果为0；

（4）局部变化量正负性∑△BIIn＜－ξ2

其中ξ2为传感器综合误差的绝对值，如果该式成立，则判断结果为1，否则，判断结果为0；

（5）路径中点取值大小｜Bm｜＞ξ3

其中Bm为路径中点传感器的测量值；ξ3为传感器综合误差的绝对值，如果该式成立，则判断结果为1，否则，判断结果为0；对各类绕组形变，五项指标的判断结果如表2所示。

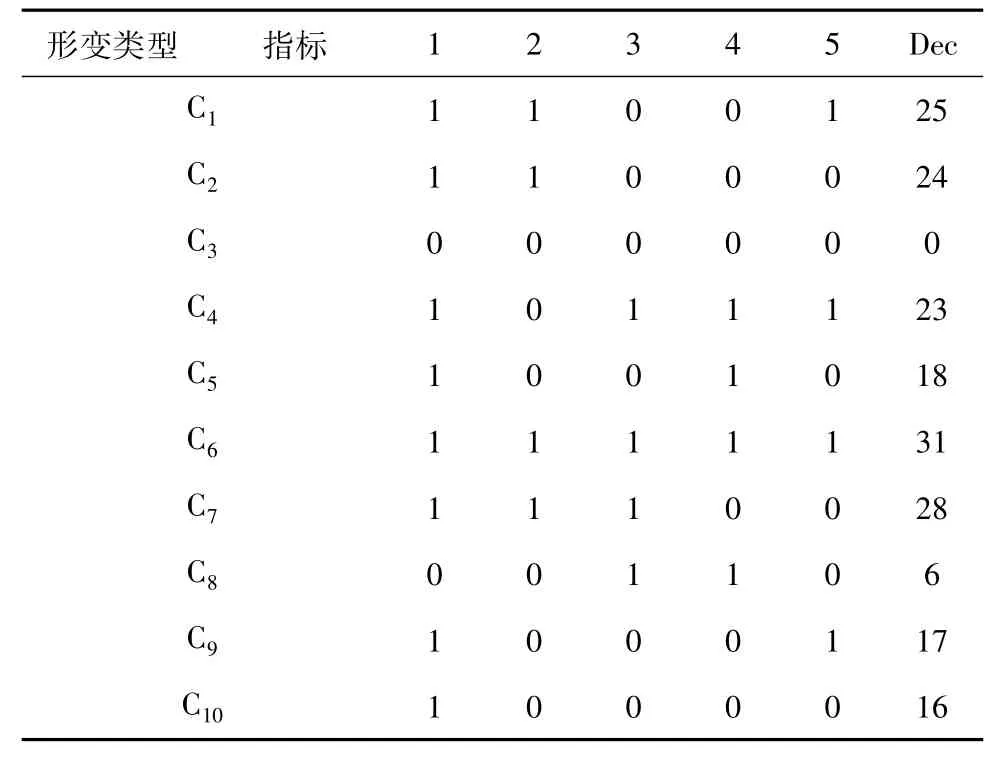
表2 不同绕组形变的各项指标判断结果Tab.2 Indicators values of different winding deformations

如表2所示，若将五个指标按照指标序号由高到低构成二进制数的五位，并将二进制数转换为相应的十进制数。可以看出，十种形变对应于不同的十进制数，因此，用这五种指标可以准确地将变压器绕组的形变进行分类。

3 变压器绕组形变判断方法的研究

3.1 变压器绕组形变的判断方法

3.1.1 变压器绕组形变与否的判断

将磁场在路径上的分布数据按照其测点序号构造成多维向量，其中，绕组正常时的向量记作B0，绕组形变后的向量记作B1。将B0记录并储存，作为指纹量；在变压器运行过程中，通过实时对比B0和B1的差异大小，来判断变压器绕组发生形变的严重程度。

计算多维向量差异性的算法有很多，如欧氏距离、余弦距离、曼哈顿距离等。当变压器绕组形变发生后，其磁场在路径上的分布与正常时的分布仍有较高的相关性，因此，不宜采用计算向量独立性算法，本文选择欧氏距离作为向量差异性的计算方法，欧氏距离的定义为：

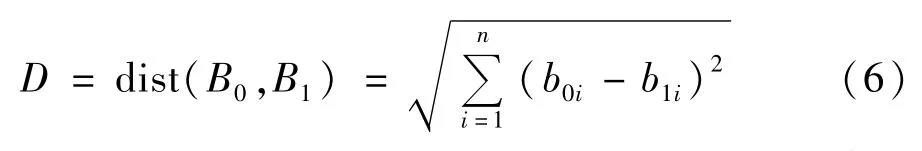
式中 B0＝（b01，b02，b03，…，x0n）；B1＝（b11，b12，b13，…，b1n）；i为测点编号；n为测点数。

在用欧氏距离计算变压器绕组发生形变与否时，只要制定适当的阈值，当欧氏距离大于该阈值时，即认为变压器绕组发生形变。设阈值为Dmin，其值应在计及传感器测量误差、仿真误差和一定裕度情况下来制定。

由欧氏距离的定义可知，测点数将影响其值的大小，因此，在确定Dmin之前，应先对传感器的安装进行优化。

3.1.2 传感器的安装优化

传感器的安装应在满足监测任务的同时保证经济性，即传感器个数尽可能少。变压器绕组形变监测的任务包括绕组形变的分类和绕组形变程度的确定两方面的任务。

（1）绕组形变分类对测点的要求

由2.5的结论，对变压器绕组形变的分量需要计算五个指标，计算这五种指标必不可少的测点有：路径中点；路径上半部分（区域I）和下半部分（区域II）对称位置处的测点。因此，对变压器绕组形变分类需要2n＋1（n＝1，2，3，…，90）个测点。

（2）形变程度判断对测点的要求

用欧氏距离计算某种绕组形变时，欧氏距离越大则反应该种形变越灵敏，传感器的固有测量误差对判断结果的影响也越小，因此，在满足经济性的要求下，测点越多越好。

如果测点数目确定，测点的位置也会影响欧氏距离的大小，故需对测点的安装位置进行优化。

（3）测点优化

由1.2节，满足变压器绕组形变分类和程度的判断的测点至少需要3个。路径中点已定，仍需对区域I和II处传感器安装位置进行优化。

对于所有形变，欧氏距离均取最大值是不可能的，因此，优化目标为：对所有的形变，欧氏距离的和最大。

由欧氏距离的定义，某种形变的欧氏距离为：

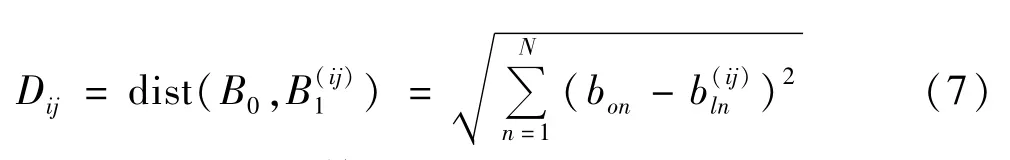
式中ij表示第i种形变，形变程度为j%；B0为指纹量；B1（ij）为形变后磁场路径分布；n为测点编号；N为测点数。

各传感器的测量值彼此独立，∑Dij取得最大值，只需在各个测点处的∑（b0n-b1n（ij））2（n＝1，2，3，…，181）最大即可，又因为传感器必须对称安装，只需要让∑（b0n-b1n（ij））2（n＝1，2，3，…，90）最大即可。

目标函数为：

式中ij表示第i种形变，形变程度为j%；n＝1，2，…，90；b0n为测点 n磁场的正常值；b1n为测点 n磁场的实测值。

随着测量位置的不同，R取值的曲线如图7所示。

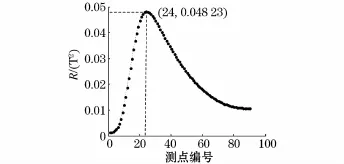
图7 测点位置对R取值的影响Fig.7 Effect of measuring point to the value of R

由图7，在测点24处R取得最大值，距离测点24越远的测点，其R值越小。

当安装3个测点时，选择的测点编号为24，91，158。安装5个测点时，所选测点编号为24，25，91，157，158。如果安装测点数大于5个时，应依据绕组形变监测的要求和R值的分布来进行选择。

3.1.3 形变程度判断

在测点数为3时，变压器绕组形变的欧氏距离与形变程度的关系曲线如图8所示，其中图8（a）为欧氏距离与低压绕组形变程度的关系曲线，图8（b）为欧氏距离与高压绕组形变程度的关系曲线。

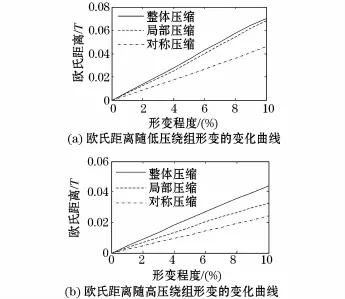
图8 欧氏距离随形变程度的变化曲线Fig.8 Euclidean distance increases with the degree of deformation of the curve

由图8可知，对于不同种类的形变，磁场分布受形变的影响程度不尽相同，对同程度的形变，低压侧形变对磁场影响大于高压测，不对称形变对磁场的影响大于对称形变。因此，变压器绕组的不同种形变应制定不同的判断阈值。

将形变的严重程度分为轻微、中度、严重、重度四个等级，相应的阈值制定，如表3所示，Di1、Di2、Di3分别为第i种形变对应的三个判定界限。

表3 变压器绕组形变严重程度定义Tab.3 Defined severity of deformation of transformer winding

表3依据对形变严重性的规定，对不同种类的形变制定不同的欧氏距离界限。在对绕组形变进行判定时，应先对形变进行分类，然后，再按照该类形变对应的欧氏距离界限进行形变严重程度的判断。

4 结束语

根据变压器的电磁关系，用ANSYS建立了变压器绕组正常和形变后的模型。通过深入研究不同类别、不同程度的变压器绕组形变与其磁场分布规律的关系，提出在变压器适当的位置安装磁场传感器，依据磁场传感器对磁场的测量实现对变压器绕组的在线监测。然后，根据对绕组形变在线监测的要求，提出了形变的判定方法和传感器的安装的优化方法。结果表明，在变压器铁芯间隙安装3个传感器即可实现对变压器绕组形变的分类以及严重程度的判断。文章针对双绕组变压器形变进行了研究，对于三绕组变压器形变磁场分布规律、形变检测算法以及传感器的安装优化仍需要进一步的研究。