Zoeppritz方程叠前多参数反演及密度敏感性分析

郭 强 张宏兵* 曹呈浩 韩飞龙 尚作萍

(①河海大学地球科学与工程学院，江苏南京 210098； ②中科院地质与地球物理研究所，北京 100029；③河海大学力学与材料学院，江苏南京 210098)

·综合研究·

Zoeppritz方程叠前多参数反演及密度敏感性分析

郭 强①张宏兵*①曹呈浩②韩飞龙①尚作萍③

(①河海大学地球科学与工程学院，江苏南京 210098； ②中科院地质与地球物理研究所，北京 100029；③河海大学力学与材料学院，江苏南京 210098)

基于Zoeppritz方程或其近似公式的叠前地震反演应用广泛，但多参数(尤其是密度参数)的同步反演结果不稳定。通过边界保护正则化和马尔科夫随机域的软约束建立反演目标函数，采用精确Zoeppritz方程进行反演，并使用快速模拟退火算法解非线性优化问题。数值结果表明，在小角度时，密度参数对角度变化不敏感，但对反射系数绝对值变化的贡献度最大；二维合成数据测试结果表明，该反演算法采用小角道集可以反演出满意的密度结果； 实际资料反演结果提供了详细的地层信息，且与测井数据基本吻合。

叠前多参数反演 密度敏感性 Zeoppritz方程 边界保护正则化 马尔科夫随机域

1 引言

地震反演是一种最有效的地震数据定量解释方法之一，根据其采用的正演物理模型，主要分为褶积模型反演和全波形反演[1,2]。褶积模型反演，无论在叠前还是叠后，都已得到广泛的商业应用；虽然基于声波方程的全波形反演技术在地震成像上已有成功应用，但基于弹性波动方程的全波形反演尚在理论探索阶段[2]。此外，各种最优化算法在地震反演中得到广泛应用，如广义线性反演法[3]，共轭梯度法[4]和模拟退火法[5]等。其中快速模拟退火法[6，7]凭借其不依赖初始模型和不易陷入局部最小值的优势，已在很多领域得到成功应用。

目前基于AVO理论的叠前地震反演应用广泛，它直接利用信息丰富的叠前道集数据，可以同步获得纵波速度、横波速度和密度[8]。但叠前地震反演仍然存在诸多问题，尤其是多参数反演结果的不稳定性问题[9，10]。由于精确Zoeppritz方程的表达式计算过程复杂，现有的文献及商业化软件多使用其近似式计算叠前道集反射系数，如Aki-Richard近似式[11]、Shuey近似式[12]和Fatti近似式[13]等，但这些近似式需要一定的假设条件，会导致计算误差[14]， 特别不利于密度参数的准确提取[15，16]。此外，叠前地震反演需要解决反演病态问题[17]和地震带限问题[18]，有关反演病态问题可以通过正则化方法得到解决[19-21]， 如边界保护正则化方法[22-24]， 而带限问题需要使用测井数据进行约束反演。

不同参数之间的差别会导致同步反演结果不稳定，体现为反演的弹性参数对于振幅和角度变化的敏感性。密度参数反演一直是业界研究的重点，Kabir等[25]的研究表明密度参数和速度参数对反射系数变化的贡献度呈互耦关系，其中密度在小角度时贡献度较大，而速度在大角度时贡献度较大，因此需要广角道集进行反演才能解耦密度和速度信息； Zong等[26，27]指出流体模量和杨氏模量中的密度项很难被准确估算，因为密度对振幅变化不敏感，因而直接计算得到的流体模量和杨氏模量并不准确； Liang等[28]提出了改进的Fatii方程，该方程突出密度优势并提高密度参数对角度变化的敏感性，进而可以得到更准确的反演密度结果。

研究弹性参数中的密度参数非常必要，尤其是研究多参数同步反演中的密度敏感性。首先，建立边界保护正则化的目标函数并结合快速模拟退火算法进行最优化；其次，分析Zoeppritz方程中反射系数对密度参数和入射角变化的敏感性；最后，通过合成数据和实际资料测试验证本文提出的方法。

2 方法原理

2.1 正演模型

叠前地震反演是基于褶积模型的反演，其理论基础是AVO理论，即描述平面波反射和透射系数相对入射角变化的Zoeppritz方程，其矩阵表达式为[11]

(1)

其中

(2)

式中：R是反射系数；T是透射系数；v是速度；ρ是密度； 下标“P”和“S”分别表示纵波和横波， “1”和“2”分别代表入射介质和透视介质；θ1和θ2分别为纵波的入射角和透射角；φ1和φ2分别为转换横波的反射角和透射角。

2.2 目标函数

通常使用褶积模型表征波阻抗反演的数学模型，即

Y=W(θ)*R(θ)+N

(3)

式中：Y为地震记录；W(θ)为角度震源子波；R(θ)为地震反射系数序列；N为随机噪声。一般情况下，假设N服从高斯分布，其数学期望为零，协方差为σ。考虑到叠前反演是一个病态问题，需要在目标函数中引入先验信息约束，采用惩罚最小平方或者最大后验概率估计，则目标函数可以表示为测量数据估算可信度项、先验信息项和约束项之和，即

J(Z)=J1(Z)+λ1J2(Z)+λ2J3(Z)

(4)

式中：J1为数据项；J2为先验项；J3是约束项；φ[·]为势函数；C1和C2为邻域内数据的点集；D(Z)为模型参数的梯度值；k是平滑阶次；Z为待反演的模型参数，即纵波速度、横波速度和密度。目标函数中有3个正则化参数：用于平衡数据项和先验项之间的相互影响的“平滑参数”λ1和λ2，用于在检测的不连续处调节梯度值的“刻度参数”δ。此外，叠前多参数同步反演的先验项J2由三部分组成

J2=J2P(vP)+J2S(vS)+J2D(ρ)

(5)

式中：J2P、J2S和J2D分别为vP、vS和ρ的先验项。为此，对于三个模型参数，其对应的δ值是不相同的。在式(4)中，目标函数的先验项和约束项是以势函数φ的形式表达；J3项的表达形式与J2项相同，但其仅在有测井数据的地震道处表达。

332332123321S123321233233

图1 关于像素点S的MRF的邻域系统一阶邻域包含标有“1”的4个点，n阶邻域包括标有比n小的所有点

2.3 最优化算法

反演问题可以看作是一个使目标函数达到极小的过程。式(4)中模型参数与测量数据之间呈现高度的非线性，线性类反演方法很难使该目标函数达到全局最优解，因此，使用快速模拟退火(FSA)算法[5，6]完成目标函数极小化。FSA不需要计算目标函数的偏导数，易于实现；并且不依赖于初始模型的选取，不易陷入局部最优解。采用依赖于温度的似Cauchy分布产生新的扰动模型，即

Z(m+1)=Z(m)+T(m)sign(ξ-0.5)×

(6)

式中：Z(m)和Z(m+1)分别为三参数当前值和扰动后的值； [Zmin，Zmax]为三参数的取值范围；ξ为[0，1]内的随机数；T(m)是当前的温度值。在每次迭代中，模型参数扰动后的值被接受的概率为

(7)

式中： ΔE是目标函数在模型参数扰动前后的能量差；h是预设定的常数。可见，每次迭代中模型参数被接受(或拒绝)的概率与目标函数能量的改变量有关。

3 密度敏感性分析

在地震反演中，密度项的获取一直是个难题。因此，基于叠前反演的理论公式(精确Zoeppritz方程)，进行多参数同步反演中的密度参数敏感性的数值分析。

为了便于分析单个参数的敏感性，将式(1)中的多参数矩阵M改写为

(8)

通过改变一个参数而固定其他两种参数的方法，分析两类模型反射系数对各参数和入射角变化的敏感性。图2为第一类模型(正反射界面)反射系数随入射角的变化曲线。由图2c可以看出，在小角度范围内，曲线接近于水平(梯度为零)，并且不同密度的曲线基本平行，而随着入射角的增加，各曲线的梯度逐渐改变。这表明，在小角度时，密度参数对角度变化不敏感，即密度参数的改变并不会影响AVO曲线的变化趋势，因此在常规梯度类AVO反演中，采用小角道集难以准确反演密度，而需要覆盖近中、远炮检距的广角道集才能获取密度信息。图2a和图2b中曲线反映出，纵横波速度参数也在适中和较大入射角范围内才对入射角的变化敏感。

进一步分析图2可以发现，各参数(vP、vS和ρ)曲线在不同入射角度范围内的错开程度是不同的，这表明不同参数在不同角度下对反射系数的贡献度有所差异[25，31]。由图2c可见，改变密度参数值后分别对应的五条曲线在小角度时错开最明显，意味着密度在小角度时对反射系数的贡献度(导致纵波反射系数绝对值改变的程度)最大，而随着入射角度的增加，贡献度降低；而纵横波速度对反射系数的贡献度呈现出相反的规律。图3是第二类模型(负反射界面)的反射系数随入射角的变化曲线，显示出相同的变化规律。需要指出的是，以上分析结果适用于纵横波速度比变化缓慢的地层，这符合大多数地层的特点。

由以上分析可知，在小角度时，由于密度的改变(或扰动)会产生较大的反射系数绝对值的变化，使目标函数的能量差异变化增大，从而在模拟退火算法中，接受(或拒绝)该扰动的概率会增加，进而提高算法对密度参数的敏感性，提高密度反演结果的准确性。

图2 第一类模型纵波反射系数对纵波速度(a)、横波速度(b)和密度(c)的敏感性分析

图3 第二类模型纵波反射系数对纵波速度(a)、横波速度(b)和密度(c)的敏感性分析

4 合成数据试算

二维模型为一个断背斜构造(图4a～图4c)，横向共有61个CDP，间隔为12.5m，每道共151个采样点，采样间隔为2ms。每个CDP有17个角道集(角度间隔为3°，角度覆盖范围为0°～48°)。通过Zoeppritz方程计算反射系数，子波采用主频分别为35、33和31Hz的带限雷克子波(分别对应小、中和大角道集)，并基于褶积模型合成地震道集。图4d为纵波速度初始模型(与真实模型的相关系数为0.65)，密度初始模型与纵波速度初始模型相似。图5为CDP 31的合成角道集。将第15道和第45道作为虚拟井(式(4)中的测井约束项J3)对反演过程进行约束。

使用0°～12°，24°～36°和36°～48°三组角度范围不同的角道集进行三参数反演，结果如图6所示。对比这些反演结果：可见纵波速度和横波速度的反演结果之间差异较小，24°～36°角道集反演的纵波速度结果与真实模型(图4a)吻合较好，尤其是断层处的特征明显，36°～48°角度的反演结果的地层分界面处不够清晰，这可能是由于大角道集距数据受调谐效应影响的结果；密度的反演结果比纵横波速度的反演结果差，三组道集密度反演结果与真实模型(图3c)的相关系数分别为0.86(0°～12°)、0.76(24°～36°)和0.73(36°～48°)，小角度道集反演的密度结果精度最高。取CDP 31(图6中虚线所示)的三组密度反演结果与真实模型进行对比(图7)，0°～12°角道集的密度结果与真实模型吻合最好。这表明，本文算法使用小角度道集可以取得较满意的密度反演结果，但是，如果想同步获得准确的三参数结果，需要覆盖近中、远炮检距的角道集。

图4 纵波速度(a)、横波速度(b)和密度(c)的真实模型及纵波速度的初始模型(d)

图5 CDP 31的合成角道集入射角范围为0°～48°，角度间隔为3°

图7 CDP 31三组角道集密度反演结果对比

5 实际数据测试

图8为中国南部M工区的一条二维任意线叠加剖面，共有1981个CDP。每个CDP的角道集均有15道，角度范围为3°～45°，间隔为3°，道间距为12.5m，时间采样间隔为2ms。三口井分别位于CDP 53(井1)、CDP 601(井2)和CDP 1745(井3)，用井1和井2的测井数据进行约束，井3进行验证。

图8 M工区二维地震剖面

图9 纵波速度(a)及密度(b)的初始模型

应用工区内几个主要地层的参数建立了纵波速度和密度的初始模型(图9)。初始模型合成的地震道集与实际地震数据的相关系数仅为0.477。

在反演中，结合了高阶和低阶邻域，即当退火温度T>0.005°时为三阶，当0.005°>T>0.001°时为二阶，当T<0.001°时为一阶。优化方法FSA的初始温度为0.05°，终止温度为0.00001°，温度衰减系数为0.9，并在反演过程中，逐渐降低λ值，而逐渐增大δ值。最优化算法和正则化参数与合成数据测试相同。

井3中的三套地层为泥岩、石灰岩(目的层)和砂泥岩，对应时间段分别为1680～1730ms、1730～1803ms和1803～1850ms；井2中也可见三套地层，其中泥岩和砂泥岩与井3中的相同，对应时间段分别为1570～1600ms和1725～1780ms，但井2中的石灰岩地层与井3中不同，这给井间约束增加了难度。图10分别为3°～15°、21°～33°和33°～45°角道集的密度反演结果。对比图10中的三组反演结果可见，小角道集反演的密度结果对地层细节信息(图10a中箭头所指)的分辨率最高。此外，由CDP 1745的三组密度反演结果与井3的密度测井曲线对比(图11)可见，三组密度反演结果与测井曲线基本吻合，其中，入射角3°～15°的密度反演结果(图11上)

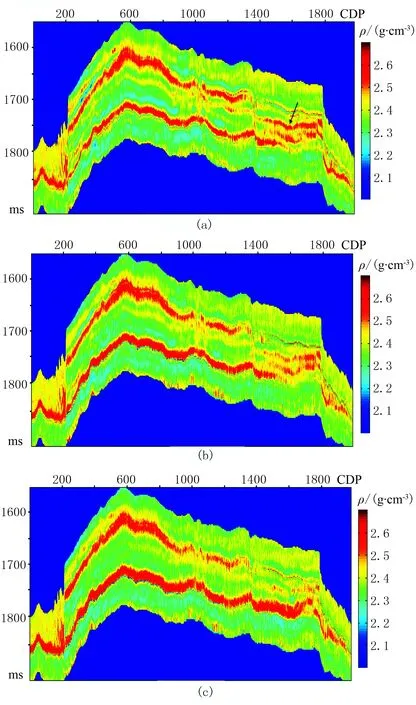
图10 实际地震资料不同角道集的密度反演结果

在1780～1810ms目的层段与测井曲线吻合最好，但是在目的层段上部(1680～1710ms)出现奇异值，这可能是随机算法在反演过程中的不稳定性造成的误差。

6 结论与讨论

本文基于精确Zoeppritz方程并结合边界保护正则化和MRF邻域建立叠前反演目标函数，并采用快速模拟退火算法进行最优化反演，着重分析了多参数同步反演中密度参数的反演问题，合成数据测试及实际资料反演取得了较好的效果。

数值分析结果表明，密度参数在小角度时对反射系数绝对值变化的贡献程度最大，随着角度的增加，贡献度降低；纵横波速度参数对反射系数的贡献度呈相反的规律。

图11 CDP 1745的三组角道集密度反演结果与井3密度测井曲线的对比

合成数据测试表明，本文算法可以在小角度情况下获得满意的密度反演结果；在实际资料反演中，获得了带有构造细节的密度参数模型，并与测井资料基本吻合。但三参数的反演结果相互制约，获得较好的密度反演结果，通常是以牺牲纵横波速度的反演精度为代价。

[1] 杨文采.地球物理反演的理论与方法.北京：地质出版社，1997.

[2] Virieux J，Operto S.An overview of full-waveform inversion in exploration geophysics.Geophysics，2009，74(6)：WCC1-WCC26.

[3] Tarantola A，Valette B.Generalized nonlinear inverse problems solved using the least squares criterion.Review of Geophysics and Space Physics，1982，20(2)：219-232.

[4] Bae H S，Pyun S，Chung W et al.Frequency-domain acoustic-elastic coupled waveform inversion using the Gauss-Newton conjugate gradient method.Geophysi-cal Prospecting，2012，60(3)：413-432.

[5] 姚姚.地球物理非线性反演模拟退火法的改进.地球物理学报，1995，38(5)：643-650.

Yao Yao.Improvement on nonlinear geophysical inversion simulated annealing.Chinese Journal of Geophysics，1995，38(5)：643-650.

[6] 张霖斌，姚振兴，纪晨等.快速模拟退火算法及应用.石油地球物理勘探，1997，32(5)：645-660.

Zhang Linbin，Yao Zhenxing，Ji Chen et al.Fast simulated annealing algorithm and its application.OGP，1997，32(5)：654-660.

[7] Zhang H，Shang Z，Yang C.A non-linear regularized constrained impedance inversion.Geophysical Prospecting，2007，55(6)：819-833.

[8] Chiappa F，Mazzotti A.Estimation of petrophysical parameters by linearized inversion of angle domain pre-stack data.Geophysical Prospecting，2009，57(3)：413-426.

[9] Down J E.Seismic Paramter Estimation from AVO Inversion [D].University of Calgary，Canada，2005.

[10] 田军，吴国忱，宗兆云.鲁棒性AVO三参数反演方法及不确定性分析.石油地球物理勘探，2013，48(3)：443-449.

Tian Jun，Wu Guochen，Zong Zhaoyun.Robust three-term AVO inversion and uncertainty analysis.OGP，2013，48(3)：443-449.

[11] Aki K，Richards P G.Quantitative Seismology：Theory and Methods.W.H.Freeman and Co.，1980.

[12] Shuey R T.A simplification of the Zoeppritz equa-tions.Geophysics，1985，50(4)：609-614.

[13] Fatti J L，Smith G C，Vail P J et al.Detection of gas in sandstone reservoirs using AVO analysis：A 3-D seismic case history using the Geostack technique.Geophysics，1994，59(9)：1362-1376.

[14] 邓炜，印兴耀，宗兆云等.基于逆算子估计的高阶AVO非线性反演.石油地球物理勘探，2016，51(5)：955-964.

Deng Wei，Yin Xingyao，Zong Zhaoyun et al.High-order nonlinear AVO inversion based on estimated inverse operator.OGP，2016，51(5)：955-964.

[15] Zhi L X，Chen S Q，Li X Y.Amplitude variation with angle inversion using the exact Zoeppritz equations—Theory and methodology.Geophysics，2016，81(2)：N1-N15.

[16] 黄捍东，王彦超，郭飞等.基于佐普里兹方程的高精度叠前反演方法.石油地球物理勘探，2013，48(5)：740-749.

Huang Handong，Wang Yanchao，Guo Fei et al.High precision prestack inversion algorithm based on Zoe-ppritz equations.OGP，2013，48(5)：740-749.

[17] Chemingui N，Biondi B.Seismic data reconstruction by inversion to common offset.Geophysics，2002，67(5)：1575-1585.

[18] Ghosh S K.Limitations on impedance inversion of band-limited reflection data.Geophysics，2000，65(3)：951-957.

[19] 吉洪诺夫，阿尔先宁著；王秉忱译.不适定问题的解法.北京：地质出版社，1979.

[20] Sen M K，Roy I G.Computation of differential seismograms and iteration adaptive regularization in pre-stack waveform inversion.Geophysics，2003，68(6)：2026-2039.

[21] 张丰麒，金之钧，盛秀杰等.贝叶斯三参数低频软约束同步反演.石油地球物理勘探，2016，51(5)：965-975.

Zhang Fengqi，Jin Zhijun，Sheng Xiujie et al.Bayesian prestack three-term inversion with soft low-frequency constraint.OGP，2016，51(5)：965-975.

[22] 张宏兵，尚作萍，杨长春.波阻抗反演正则参数估计.地球物理学报，2005，48(1)：181-188.

Zhang Hongbing，Shang Zuoping，Yang Changchun.Estimation of regular parameters for the impedance inversion.Chinese Journal of Geophysics，2005，48(1)：181-188.

[23] Zhang H，Shang Z，Yang C.Adaptive reconstruction method of impedance model with absolute and relative constraints.Journal of Applied Geophysics，2009，67(2)：114-124.

[24] Yan Z，Gu H.Non-linear prestack seismic inversion with global optimization using an edge-preserving smoothing filter.Geophysical Prospecting，2013，61(4)：747-760.

[25] Kabir N，Crider R，Ramkhelawan R et al.Can hydrocarbon saturation be estimated using density contrast parameter？CSEG Recorder，2006，31(6)：31-37.

[26] Zong Z，Yin X，Wu G.AVO inversion and poroelasti-city with P- and S-wave moduli.Geophysics，2012，77(6)：N17-N24.

[27] Zong Z，Yin X，Wu G.Elastic impedance paramete-rization and inversion with Young’s modulus and Poisson’s ratio.Geophysics，2013，78(6)：N35-N42.

[28] Liang Lifeng，Zhang Hongbing，Dan Zhiwei et al.Prestack density inversion using the Fatti equation constrained by the P- and S-wave impedance and density.Applied Geophysics，2017，14(1)：133-141.

[29] Charbonnier P，Blanc-Féraud L，Aubert G.Determini-stic edge-preserving regularization in computed imaging.IEEE Transactions on Image Processing，1997，6(2)：298-311.

[30] Geman D，Yang C.Nonlinear image recovery with half-quadratic regularization.IEEE Transactions on Image Processing，1995，4(7)：932-946.

[31] Huang Handong，Zhang Ruwei，Shen Guoqiang et al.Study of prestack elastic parameter consistency inversion methods.Applied Geophysics，2011，8(4)：311-318.

*江苏省南京市河海大学地球科学与工程学院，210098。Email：hbzhang@hhu.edu.cn

本文于2016年10月3日收到，最终修改稿于2017年8月30日收到。

本项研究受国家自然科学基金项目(41374116、41674113)和中国海洋石油总公司科研项目(CNOOC-KJ125 ZDXM 07 LTD NFGC 2014-04)联合资助。

1000-7210(2017)06-1218-08

郭强，张宏兵，曹呈浩，韩飞龙，尚作萍.Zoeppritz方程叠前多参数反演及密度敏感性分析.石油地球物理勘探，2017,52(6):1218-1225.

P631

A

10.13810/j.cnki.issn.1000-7210.2017.06.012

(本文编辑：宜明理)

郭强 博士研究生，1989年生；2012年毕业于中国地质大学(武汉)地球物理学专业，获学士学位；现于河海大学地球科学与工程学院攻读博士学位，主要从事地震数据反演与最优化算法等研究。