时频属性法薄互层预测

刘力辉 李建海 孙莹频 胡 诚

(①北京诺克斯达石油科技有限公司，北京 100192； ②成都晶石石油科技有限公司，四川成都 610041)

·综合研究·

时频属性法薄互层预测

刘力辉①李建海*②孙莹频①胡 诚②

(①北京诺克斯达石油科技有限公司，北京 100192； ②成都晶石石油科技有限公司，四川成都 610041)

1/4波长以内的薄互层厚度预测一直是勘探难题，本文主要探讨利用时频属性预测薄互层累计厚度的方法。通过薄互层楔状模型和两个叠置薄层模型，厘清薄互层累计厚度与时频属性的关系及其主要影响因素。模型研究结果表明： 净毛比、层数和互层模式都对峰值振幅—毛厚度关系有影响，其中净毛比影响最大，其次是互层数，影响最小的是互层模式； 净毛比控制峰值振幅、峰值频率与毛厚度关系，也控制调谐厚度范围； 在调谐厚度内，峰值振幅(积分能谱)与毛厚度呈单调递增线性关系，峰值频率与毛厚度呈单调递减线性关系； 积分能谱与净厚度呈线性关系，积分能谱有扩大调谐厚度范围功能，有利于计算薄互层净厚度。根据模型试算结果，在实际资料中运用人工智能方法，利用峰值振幅和峰值频率等联合计算薄互层净厚度。预测结果表明本文方法准确、可靠，实用性强。

薄互层 净毛比 毛厚度 峰值振幅 峰值频率 积分能谱 人工智能

1 引言

薄层厚度的预测方法大体可以分为两类。第一类是时间域调谐厚度法，认为λ/4(λ为地震波长)调谐厚度内，薄层反射振幅与厚度的关系为线性关系[1-3]。第二类是频率域方法，孙鲁平等[4]推导了地震峰值频率与薄层厚度的理论关系表达式，但需已知顶底反射系数比，模板为一簇曲线。

薄层互层的定量预测方法有三类。第一类是频率属性法。曾洪流等[1]提出了层分辨率的概念，利用时频分析的主频率预测薄互层净厚度[5]。第二类是振幅法[6-12]。黄文峰等[10]利用薄互层调谐规律去调谐，利用地震振幅计算净厚度。两个文献都指出-90°相位子波有利于分辨薄互层。第三类是波形法[12，13]。杨昊等[13]先构建含有薄层厚度的原子库，用匹配追踪方法将薄层反射波形和库中原子匹配，得出薄层反射系数位置和厚度。对于频率属性法，薄互层振幅谱和毛厚度及净毛比的关系还没有相应的理论公式，需要近一步发展。

2 薄互层时频特征影响因素

薄互层的时间域反射特征主要受毛厚度(砂泥岩薄互层总厚度T)和净毛比(砂岩累加厚度与毛厚度之比G)影响，还受互层层数、互层分布模式等影响[10]。那么薄互层时频特征主要受哪些因素控制呢？时频域薄互层反射的特征可由峰值振幅和峰值频率两个参数表征。薄互层反射时窗内，由多个时频点谱可以计算出一个傅氏谱，其对应的最大振幅为峰值振幅，对应的频率为峰值频率。振幅谱中低频到子波主频的积分为积分能谱。下面讨论薄互层的毛厚度、净毛比、层数和互层模式对峰值振幅的影响。

图1给出了三组薄互层楔形模型的峰值振幅与毛厚度的关系曲线。第一组模型的净毛比相同、互层层数相同、互层模式(互层由“四薄一厚”五小砂层构成，厚砂层位于底部、第四层、第三层对应分布1、2、3)不同； 第二组模型为净毛比相同、互层层数不同、互层模式相同； 第三组模型的净毛比不同、层数相同、互层模式相同。从图1发现净毛比、层数和互层模式对峰值振幅—毛厚度关系都有影响，其中净毛比影响最大，其次是互层数，影响最小的是互层模式。因此，在薄互层时频分辨率分析中，主要讨论毛厚度和净毛比的影响。

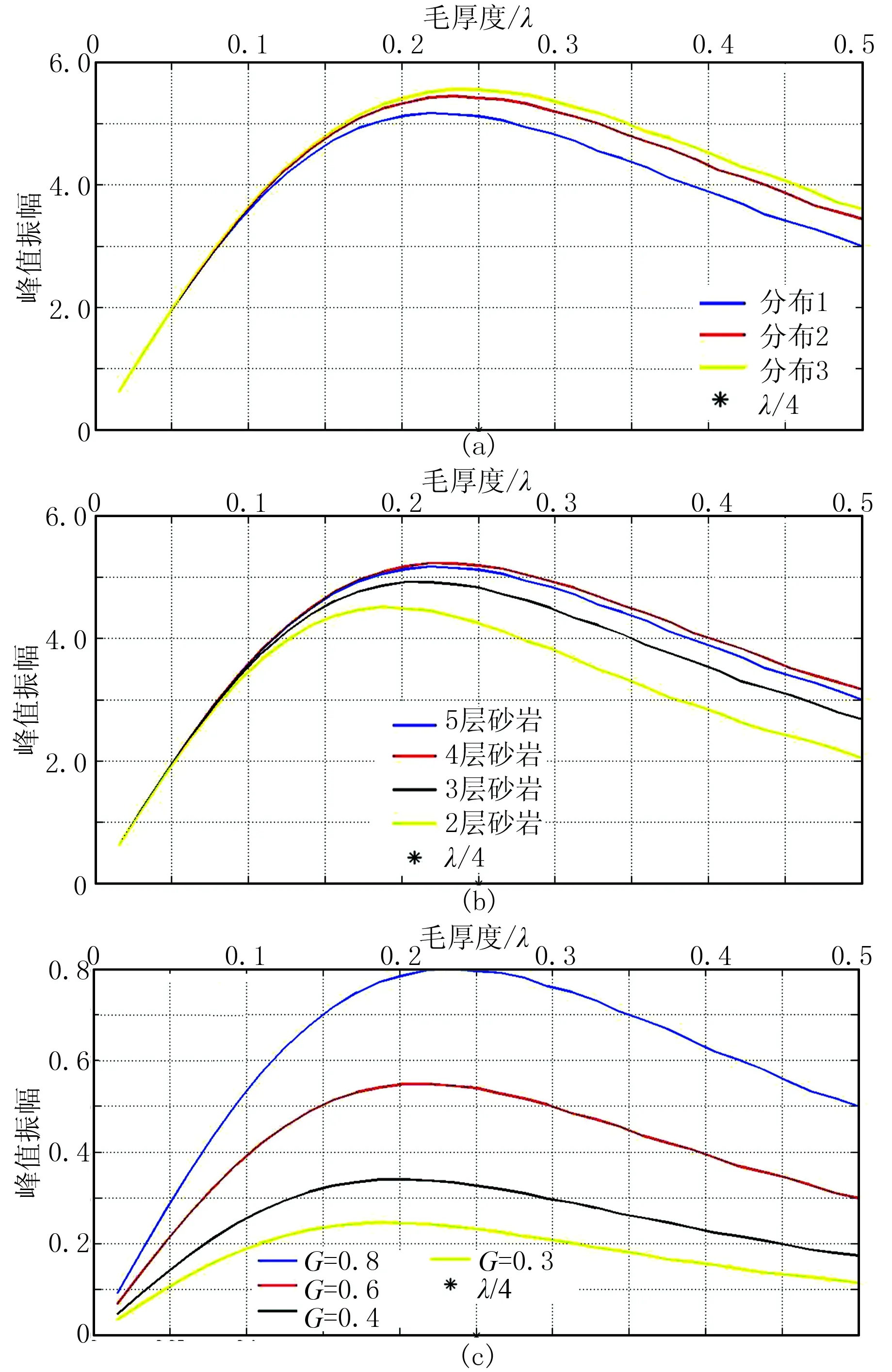
图1 三组薄互层楔形体峰值振幅与毛厚度关系曲线

图2为净毛比不同、层数相同、互层模式不同(等厚、递变)的楔形模型的地震响应。其中图2a、图2c是等厚模型，图2b、图2d是纵向厚度递变模型。图3a是图2中各模型对应的时间域振幅—毛厚度随净毛比变化曲线，图3b是时频域峰值振幅—毛厚度随净毛比变化曲线，对比两张图可以看出，时间域振幅—毛厚度关系和时频域峰值振幅—毛厚度关系相似，净毛比主要控制调谐厚度和曲线斜率，净毛比越大，调谐厚度越大。

3 薄互层的振幅谱公式

以图4两层等厚砂岩夹一层泥岩隔层的基本薄互层为例(砂岩高阻抗，泥岩低阻抗)讨论毛厚度和净毛比同峰值振幅、峰值频率的定量关系。

设薄互层砂岩净厚度Tsand与互层总厚度T的比值为净毛比G，反射系数强度为r, 则薄互层地震响应S的振幅谱(推导见附录)为[12]

|sin[πf(1-G)T]-sin(πfT)||r|

(1)

式中fd为子波主频，是已知数。可看出毛厚度和净毛比是决定峰值振幅、峰值频率等时频属性的关键参数。对上述模型给定一组净毛比，可以得出一组时频属性—毛厚度—净毛比关系曲线。

如图5所示，在薄互层顶、底反射系数比约为-1的情况下，峰值振幅和毛厚度关系与薄互层时间域振幅—厚度关系相似，但调谐点和其调谐厚度(图中*)受净毛比控制。在调谐厚度内，峰值振幅和毛厚度呈单增的线性关系。峰值频率—毛厚度线性关系也受净毛比控制，和毛厚度呈单减的的关系，不受调谐厚度影响，实用性强。积分能谱—毛厚度线性关系曲线形态类似峰值振幅，调谐厚度同样受净毛比控制，但调谐厚度加大，实用性更强。

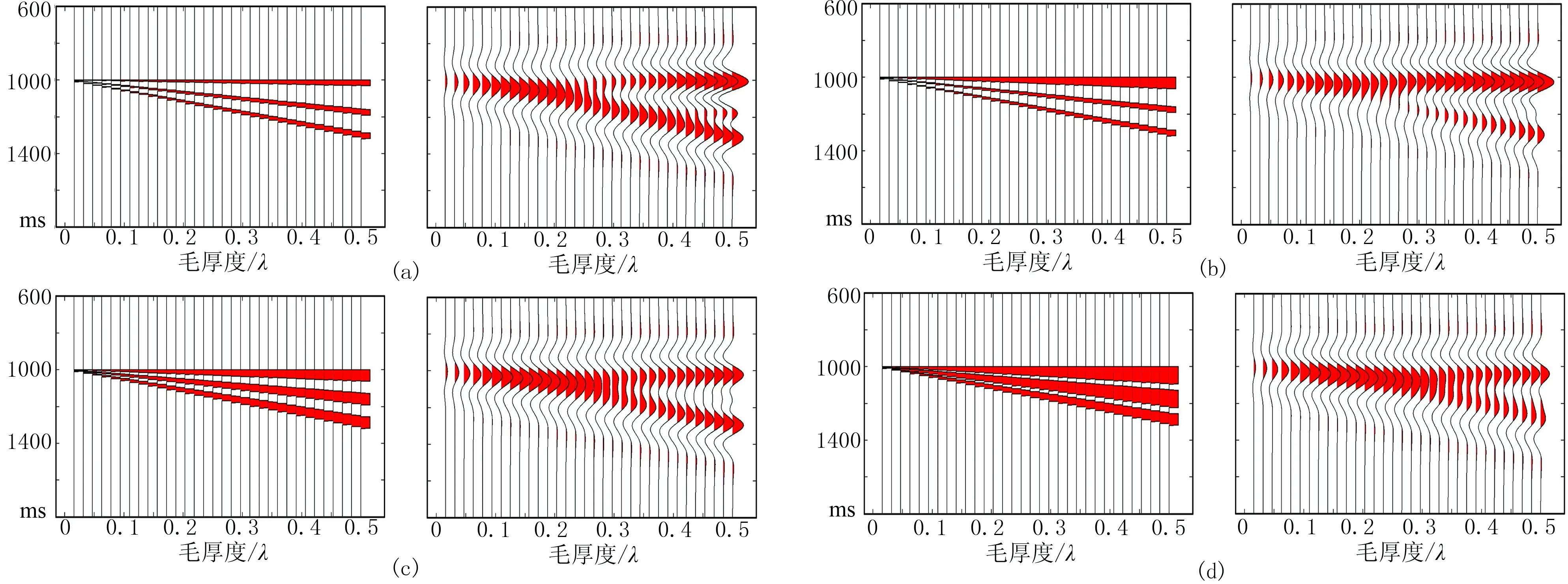
图2 不同净毛比的三层砂岩、两层泥岩隔层楔形模型(左)及其地震响应(右)

图3 平均振幅(a)和峰值振幅(b)与毛厚度的关系

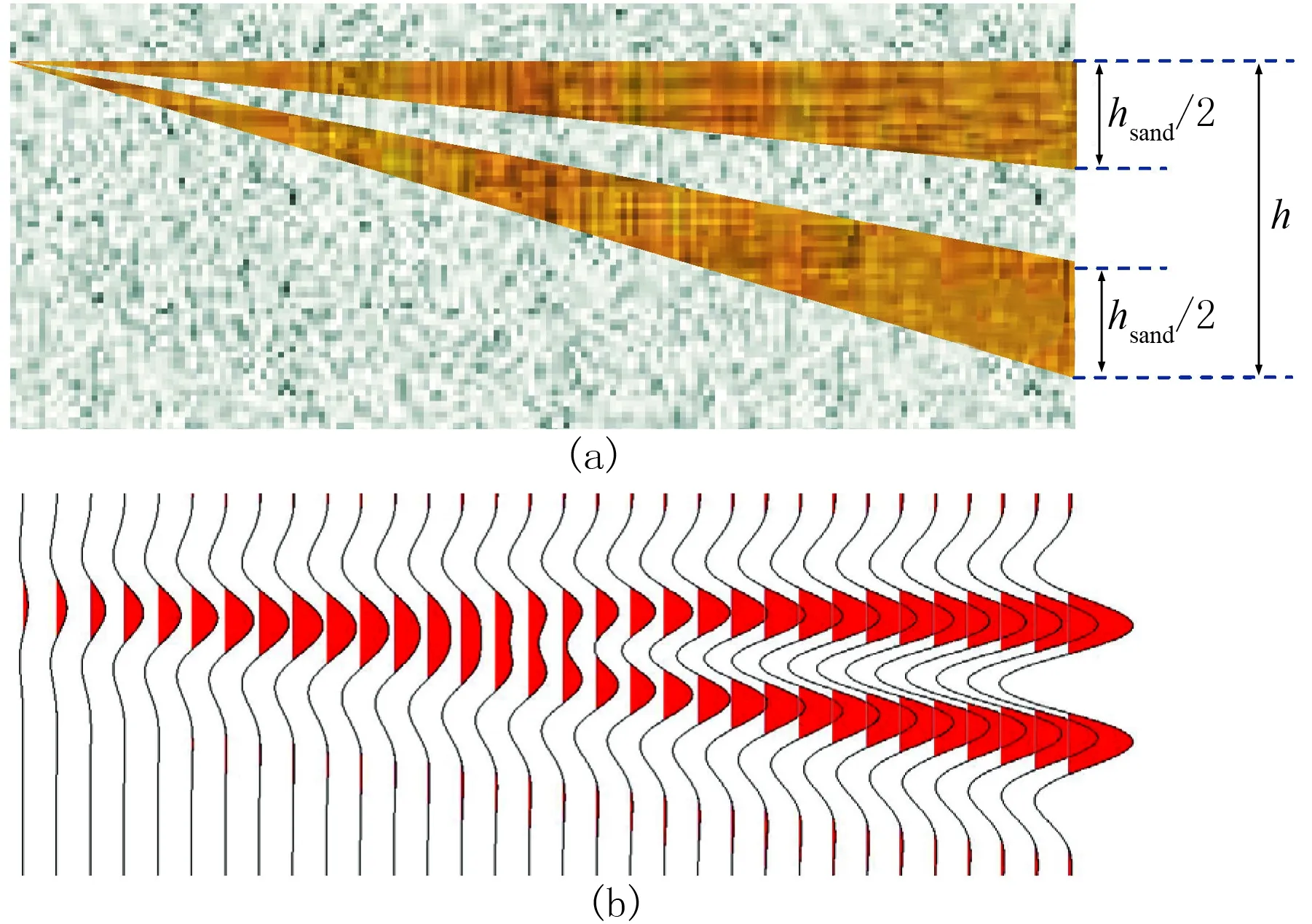
图4 薄互层楔形体(a)及其-90°相位合成地震道(b)

4 时频属性预测薄互层

目前用于提取时频属性的时频分析方法较多，常用的包括小波变换、S变换，广义S变换以及匹配追踪等方法[15-18]。由于受测不准准则的制约，应用小波变换、广义S变换等线性算法无法同时获得高时间分辨率和高频率分辨率，而应用匹配追踪算法可克服窗函数的限制，能同时在时间域和频率域精细表征信号特征[18]。因此，本文研究时频属性提取采用匹配追踪方法。

4.1 积分能谱预测净厚度

在调谐厚度内，峰值振幅AS与砂岩净厚度hsand呈单调递增的近似线性关系

hsand≈f1(AS)=k1ASk1>0

(2)

为增加峰值振幅计算净厚度的实用性，扩大调谐厚度的范围，提出了积分能谱属性。

在薄互层顶、底反射系数比约为-1情况下，在调谐厚度范围，积分能谱和净厚度呈递增的线性关系。研究发现积分限越窄，调谐厚度越大，积分限有扩大线关系应用范围的作用。图6从上到下分别为5Hz～31.25Hz(子波主频)、5～25Hz及5～15Hz的积分能谱与厚度关系曲线，可见窄频带的积分能谱属性具有扩大调谐厚度的特性，但曲线斜率变小、敏感度降低，实际应用中应选取合适的积分限。

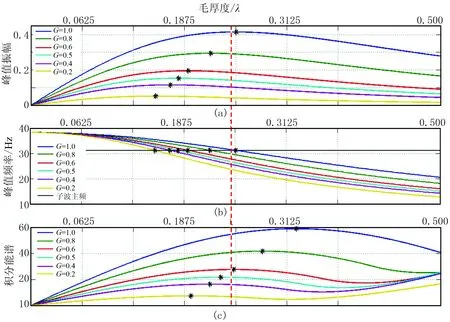
图5 不同净毛比的薄互层毛厚度与峰值振幅(a)、峰值频率(b)、带限积分能谱(c)的关系(子波主频为31.25Hz)

图6 不同频带积分能谱与毛厚度关系

4.2 峰值频率预测净厚度

当目的层毛厚度稳定时，可以用峰值频率预测净厚度。峰值频率fp与砂岩净厚度hsand近似关系

hsand≈f2(fp)=f0-k2fp

f0>fpk2>0

(3)

式中f0为砂岩净厚度逼近于0时对应的地震峰值频率。实际应用中因峰值频率不稳定，需要结合其他参数求取。

4.3 非线性映射预测净厚度

峰值振幅、积分能谱和峰值频率都与薄互层的净厚度有关，但目前还没有一个严格的解析式，为提高砂岩净厚度的估算精度，实际应用时可以利用人工智能方式，通过井震的监督学习，建立净厚度与峰值振幅、峰值频率等的非线性映射关系，计算薄互层的净砂岩厚度。人工神经网络是近些年研究热点，是人工智能研究重要组成部分。在石油勘探开发领域，目前主要用BP神经网络方法，解决井震分线性映射问题[19-22]。但BP神经网络方法存在易陷入局部最优解、效率低、横向外推能力有限等问题[23]。EANN(进化型神经网络)方法[24]采用群居寻优的方式，能有效解决过度学习问题，同时有较好的外推能力，能有效保持地震预测的沉积边界。因此本次研究选用EANN方法预测砂岩累计厚度。

5 应用实例

研究区构造上位于川西坳陷到川中隆起的过渡斜坡带上，勘探开发结果表明该区为油气长期运移的指向带，成藏条件优越[25]。本区主要目的层为沙一段，储层类型为三角洲前缘分流河道砂体。由于水体较浅，在横向上，河道分支数目较多，摆动频繁，纵向上表现为多套河道砂体叠置，分流河道砂体与分流间湾泥岩呈薄互层状分布(图7)。薄层砂体累计厚度控制了本区储层物性及含气性，进而控制储量计算结果。

测井解释结果表明，研究区沙一段单层砂体厚度在4m以内，最大累计厚度为12m，平均厚度为6.5m。而研究区原始地震资料目的层主频约为30Hz，沙一段多套砂泥岩互层在-90°地震剖面上表现为一个波谷反射，利用时间分辨率仅能识别到砂组级别(约50m，图8)。根据地震资料主频(30Hz)及砂岩速度(4300m/s)测算，砂体厚度在λ/4波长内，因此符合薄互层理论模型，可用峰值振幅、峰值频率及积分能谱通过非线性拟合求取累计砂体厚度。

由于峰值频率求取困难、稳定性较差，本次研究选择匹配追踪峰值振幅与积分能谱进行薄层厚度预测。图9为沙一段峰值振幅和积分能谱属性图，二者基本反映了本区沉积展布规律，进一步能反映砂体分布特征。从井震统计关系来看，峰值振幅和积分能谱属性数值均与累计厚度呈正相关关系，但不是确定的线性关系(图10)。

通过EANN遗传网络算法，将峰值振幅和积分能谱属性转换为砂岩厚度图(图11)。从砂岩厚度图横向分布趋势来看，砂体主要分布于分流河道微相，表现出明显的相控砂体分布特征。从砂体厚度值域分布来看，多条河道叠置交会区、河道弯道部位及正中位置，砂体厚度最大，累计厚度均在9m以上，以S13、S102井为例；其次为河道侧翼，紧挨河道边界位置，砂体累计厚度为7m，以S6、S15井为例；而远离河道部位，砂体普遍较薄，约为4m，表现为片状分布，主要位于研究区西部及南部，多条河道之间。

图7 连井小层对比图

图8 -90°相移后的地震剖面

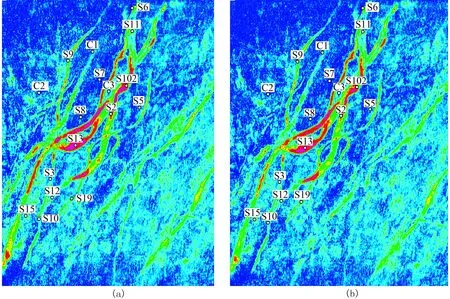
图9 沙一段峰值振幅(a)和积分能谱(b)属性图

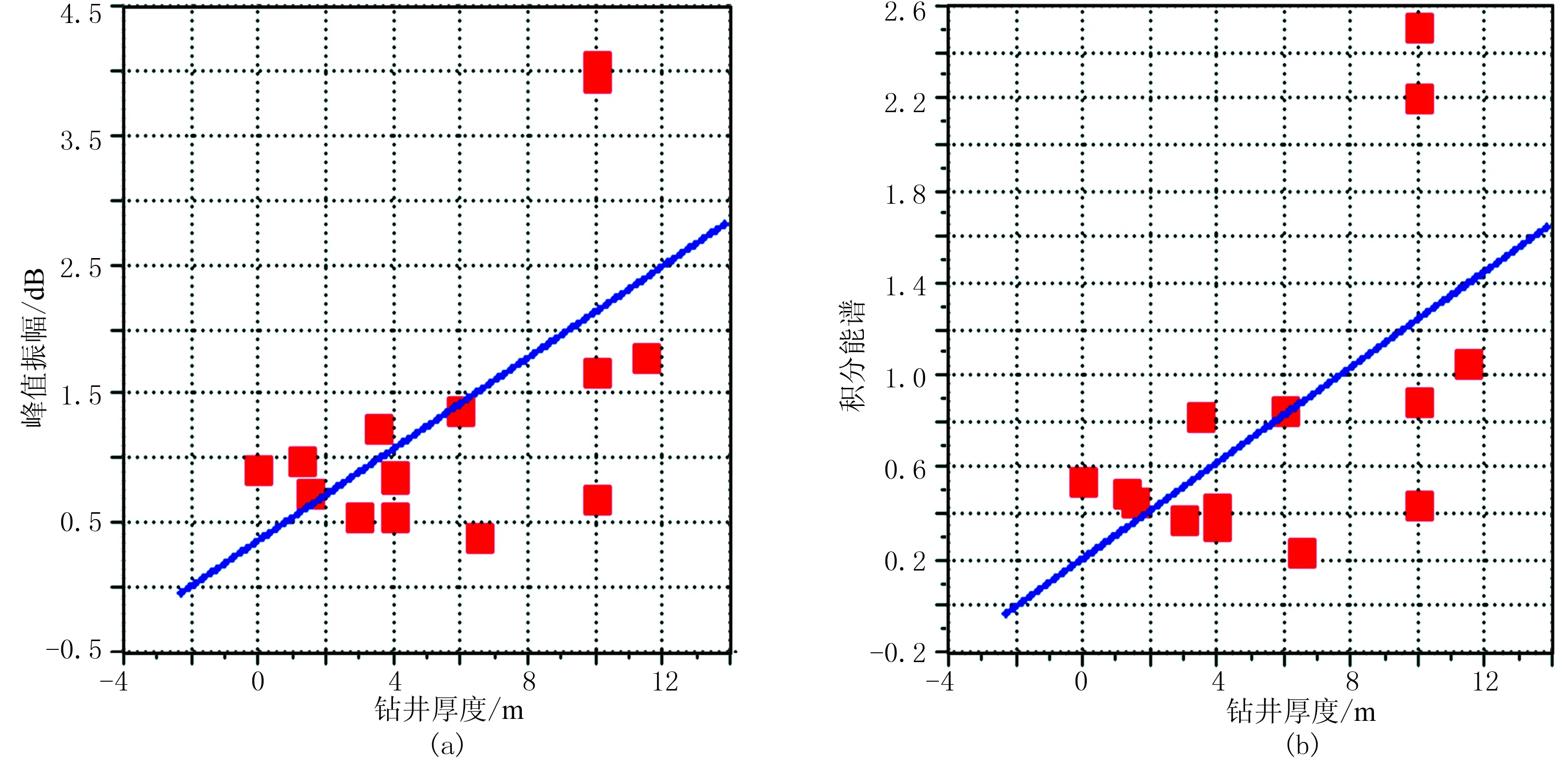
图10 沙一段峰值振幅(a)、积分能谱(b)与厚度对应关系

图11 沙一段砂体累计厚度预测图

表1为峰值振幅、积分能谱预测砂岩累计厚度与测井解释砂岩累计厚度对比结果，井震对比结果表明，预测结果与测井结果吻合度较高，最大误差不超过2m，预测结果可靠。

6 结论

影响薄互层的振幅谱主要因素是毛厚度和净毛比。在调谐厚度内，峰值振幅—净厚度呈单调递增的线性关系，积分能谱—净厚度也呈单调递增的线性关系,但调谐厚度更范围大。积分能谱的窄带积分限可扩大调谐厚度范围，增强积分能谱实用性。峰值频率—净厚度呈单减的线性关系。在实际资料中可用峰值振幅(积分能谱)、峰值频率双变量为输入，用人工神经网络预测薄互层净厚度。

本文写作得益于与中国石油勘探开发研究院西北分院相关专家的技术讨论，同时得到该分院规划所GEOSED软件的支持，在此一并致谢！

表1 地震预测薄层厚度误差统计表

[1] Zeng H，John A and Katherine G.How thin is a thin bed? An alternative perspective.SEG Technical Program Expanded Abstracts，2008，27：834-838.

[2] Puryear C I，Castagna J P.Layer-thickness determination and stratigraphic interpretation using spectral inversion：Theory and application.Geophysics，2008，73(2)：R37-R48.

[3] 凌云研究小组．应用振幅的调谐作探测地层厚度小于1/4波长地质目标.石油地球物理勘探，2003，38(3)：268-274.

Ling Yun Study Group.Application of amplitude tuning in surveying geologic target thickness less than 1/4 wavelength.OGP，2003，38(3)：268-274.

[4] 孙鲁平，郑晓东，首皓等.薄层地震峰值频率与厚度关系研究.石油地球物理勘探，2010，45(2)：254-259，271.

Sun Luping，Zheng Xiaodong，Shou Hao et al.The studies on relationship between thin layer seismic peak frequency and its thickness.OGP，2010，45(2)：258-259，271.

[5] 尹继尧，吴宝成，王维等.基于TK能量的峰值瞬时频率在薄互层预测中的应用.石油地球物理勘探，2015，50(3)：516-522.

Yin Jiyao，Wu Baocheng，Wang Wei et al.Thin interbed thickness prediction using peak instantaneous frequency of time-frequency Teager-Kaiser energy.OGP，2015，50(3)：516-522.

[6] 李庆忠.含油气砂岩的频率特征及振幅特征.石油地球物理勘探，1987，22(1)：1-23.

Li Qingzhong.The frequency and amplitude of seismic waves sandstone.OGP，1987，22(1)：1-23.

[7] 李国发，岳英，熊金良等．基于三维模型的薄互层振幅属性实验研究.石油地球物理勘探，2011，46(1)：115-120.

Li Guofa，Yue Ying，Xiong Jinliang et al.Experimental study on seismic amplitude attribute of thin interbed based on 3D model.OGP，2011，46(1)：115-120.

[8] 苏盛甫.薄储集层的反射特征和定量解释方法.石油地球物理勘探，1988，23(4)：387-402.

Su Shengfu.Thin-reservoir reflection and the quantitative interpretation method.OGP，1988，23(4)：387-402.

[9] 曲鑫，刘财，冯晅等.利用加权积分能谱方法和复数道分析技术对薄层的识别与分析.世界地质，2013，32(1):114-122.

Qu Xin，Liu Cai，Feng Xuan et al.Thin layer distinguishing and analysis by weighted integral spectrum method and complex trace analysis technique.Global Geology，2013，32(1)：114-122.

[10] 黄文锋，姚逢昌，李宏兵.薄互层调谐规律研究与净厚度估算.石油地球物理探，2012，47(4)：584-591.

Huang Wenfeng，Yao Fengchang，Li Hongbing.Regu-larities of tuning effects of thin interbedded layers and their net thickness determination.OGP，2012，47(4)：584-591.

[11] 彭达，尹成，朱永才等.扇三角洲前缘薄互层叠置砂体的敏感属性分析.石油地球物理勘探，2015，50(4)：714-722.

Peng Da，Yin Cheng，Zhu Yongcai et al.Sensitive seismic attribute analysis on thin interbed overlapped sandbodies in fan-delta front.OGP，2015，50(4)：714-722.

[12] 张玉芬，熊维纲.石油地震勘探中薄互层的反射系数序列振幅谱特征分析.地球科学，1994，19(5)：685-693.

Zhang Yufen，Xiong Weigang.Characteristic analysis of amplitude spectra of reflection coefficient of thin interbedding in oil prospecting.Earth Science，1994，19(5)：685-693.

[13] 杨昊，郑晓东，李劲松等.基于匹配追踪的薄层自动解释方法.石油地球物理勘探，2013，48(3)：429-435.

Yang Hao，Zheng Xiaodong，Li Jinsong et al.Thin-bed automatic interpretation based on matching pursuit.OGP， 2013，48(3)：429-435.

[14] 北京诺克斯达石油科技有限公司.基于偶函数地震响应以估算薄层厚度的方法和装置.中国专利： 201310528786.X，2016-08-03.

Beijing Rockstarstar Petroleum Technology Co Ltd.The Seismic Response to Even Function Estimation Method and Device Based on the Thickness of Thin Layer [P].Chinese patent：201310528786.X，2016-08-03.

[15] 陈学华，贺振华.改进的S变换及在地震信号处理中的应用.数据采集与处理，2005，20(4)：449-453.

Chen Xuehua，He Zhenhua.Improved S-Transform and its application in seismic signal processing.Data Acquisition and Processing，2005，20(4)：449-453.

[16] 张繁昌，李传辉，印兴耀.基于动态匹配子波库的地震数据快速匹配追踪.石油地球物理勘探，2010，45(5)：667-673.

Zhang Fanchang，Li Chuanhui，Yin Xingyao.Seismic data fast matching pursuit based on dynamic matching wavelet library.OGP，2010，45(5)：667-673.

[17] 董宁，杨立强.基于小波变换的吸收衰减技术在塔河油田储层预测中的应用研究.地球物理学进展，2008，23(2)：533-538.

Dong Ning，Yang Liqiang.Application of absorption and attenuation based on wavelet transform for prediction of reservoir in Tahe oilfield.Progress in Geophysics，2008，23(2)：533-538.

[18] 黄捍东，郭飞，汪佳蓓等.高精度地震时频谱分解方法及应用.石油地球物理勘探，2012，47(5)：770-780.

Huang Handong，Guo Fei，Wang Jiabei et al.High precision seismic time-frequency spectrum decomposition method and its application.OGP，2012，47(5)：773-780.

[19] 陈蓉，王峰.基于MATLAB的BP神经网络在储层物性预测中的应用.测井技术，2009，33(1)：75-78.

Chen Rong，Wang Feng.Application of MATLAB-based of BP neural network in reservoir parameters prediction.Well Logging Technology，2009，33(1)：75-78.

[20] 徐刚，张建宁，谭明友.BP人工神经网络在济阳拗陷圈闭地质评价中的应用.石油地球物理勘探，2004，39(5)：565-569.

Xu Gang，Zhang Jianning，Tan Mingyou.Application of BP artificial neural network to geologic appreciation of traps in Jiyang depression.OGP，2004，39(5)：565-569.

[21] 王桂英，白雪莲，李咏梅等.应用GeoEast系统预测煤层分布和厚度.石油地球物理勘探，2014，49(增刊1)：184-191.

Wang Guiying，Bai Xuelian，Li Yongmei et al.Coal bed distribution and thickness prediction with GeoEast.OGP，2014，49(S1)：184-191.

[22] 陈钢花，胡琮，曾亚丽等.基于BP神经网络的碳酸盐岩储层缝洞充填物测井识别方法.石油物探，2015，54(1)：99-104.

Chen Ganghua，Hu Cong，Zeng Yali et al.Logging identification method of fillings in fractures and ca-verns in carbonate reservoir based on BP neural network.GPP，2015，54(1)：99-104.

[23] 文晓涛，贺振华，黄德济.遗传算法与神经网络法在碳酸盐岩储集层评价中的应用.石油物探，2005，44(3)：225-228.

Wen Xiaotao，He Zhenhua，Huang Deji.Using genetic algorithms and neural network to evaluate carbonate reservoir.GPP，2005，44(3)：225-228.

[24] 刘志伟.遗传进化型神经网络体系结构研究[学位论文].安徽合肥：合肥工业大学，2007.

Liu Zhiwei.Research on Architecture of Genetic Evolutionary Neural Networks [D].Hefei University of Technology，Hefei，Anhui，2007.

[25] 王帅成，王多义，陈敏等.川西坳陷中段沙溪庙组天然气成藏条件分析.海洋石油，2010，30(3)：42-46，96.

Wang Shuaicheng，Wang Duoyi，Chen Min et al.Natural gas reservoir-formation condition of Shaximiao Formation in mid-band of Western Sichuan Depression.Offshore Oil，2010，30(3)：42-46，96.

附录A薄互层振幅谱公式推导

由图A-1可见，反射系数序列可表示为

由傅里叶变换，可得

R(f)=rexp[-iπfT]-rexp[iπfT]-

rexp[-iπf(T-Tsand)]+

rexp[iπf(T-Tsand)]

图A-1 简化薄互层模型

cos(πfT)-isin(πfT)-cos[πf(T-Tsand)]+

isin[πf(T-Tsand)]+cos[πf(T-Tsand)]+

isin[πf(T-Tsand)]+

=2i{sin[πf(T-Tsand)]-sin(πfT)}

Ar(f)=2|r||sin[πf(1-G)T]-sin(πfT)|

雷克子波振幅谱为

则合成记录的振幅谱为

|sin[πf(1-G)T]-sin(πfT)||r|

*四川省成都市成都晶石石油科技有限公司，610041。Email:172824397@qq.com

本文于2016年12月1日收到，最终修改稿于2017年9月28日收到。

本项研究受中国石油天然气股份有限公司“地震沉积分析软件集成应用与区带、目标评价”课题(2016B-0305)资助。

1000-7210(2017)06-1261-08

刘力辉，李建海，孙莹频，胡诚.时频属性法薄互层预测.石油地球物理勘探，2017,52(6):1261-1268.

P631

A

10.13810/j.cnki.issn.1000-7210.2017.06.017

(本文编辑：朱汉东)

刘力辉 博士，1965年生； 1988年本科毕业于石油大学勘查地球物理专业,1997年获石油大学煤田、油气地质与勘探专业硕士学位，2011年获成都理工大学地球探测与信息技术专业博士学位； 主要从事地震沉积学研究、物探技术方法及相关软件的研发。