基于波动方程重建震源子波的三维全波形反演

梁展源 吴国忱 王玉梅

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②中国石化胜利油田物探研究院， 山东东营 257022)

·偏移成像·

基于波动方程重建震源子波的三维全波形反演

梁展源*①吴国忱①王玉梅②

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②中国石化胜利油田物探研究院， 山东东营 257022)

提出一种基于波动方程重建震源子波的三维全波形反演方法，通过提取叠前炮集近炮检距的直达波作为波动方程求解的边界条件，重新求解波动方程，并记录震源点处的时间序列作为地震子波。该方法利用震源波场重建原理模拟震源爆炸沿地表传播的逆过程，在逆推过程中提取近炮检距直达波，避免了折射波、反射波以及潜水波等干扰。该方法只使用模型表层速度，可以有效降低对初始模型的依赖。对三维SEG/EAGE推覆体模型以及实际工区数据的测试结果表明，基于波动方程震源波场重建子波与输入子波只存在相位差异，经过相位调整后，将重建子波用于三维全波形反演，全波形反演速度接近真实速度，特别是在河道处的全波形反演结果更加可靠，观测记录与模拟记录在波形、相位等方面均有较好的对应，验证了算法的可行性与适用性。

地震子波 全波形反演 震源波场重建 波动方程 SEG/EAGE推覆体模型

1 引言

全波形反演(Full Waveform Inversion，简称FWI)可进行高分辨率地震速度成像，近年来逐渐发展为勘探地球物理研究的热点。FWI基于波动方程全波场数值模拟，是一个局部寻优的非线性迭代反演问题[1-3]。FWI以观测记录和合成记录的最小二乘函数作为目标函数，利用地震波的走时、振幅、相位等全波形信息反演地下介质参数，具有最高分辨率的特性[4-6]。同时，FWI也存在固有缺陷：一是效率问题，主要体现在反演伴随着巨大计算量与存储量；二是局部极小值问题，初始速度不准确、子波不匹配等因素都会使迭代陷入局部极小值。

随着计算机技术的发展，特别是GPU并行程序的应用，FWI的计算效率明显提高[7-11]，但是巨大的I/O吞吐问题依然存在。根据波动方程的求解原理，常采用震源波场重建方法解决存储问题，该方法首先由Gauthier等[12]提出并用于逆时偏移过程，在震源波场正传过程中存储边界波场，存储的边界波场的层数与使用的差分阶数有关，在检波点逆时传播的同时进行源波场重建。该方法数值精度高，但是存储量正比于有限差分算子的阶数。为了进一步减少存储量，Feng等[13]提出一种改进方案，只存储一层网格的边界波场，采用从外至内边界波场从二阶差分逐渐升到高阶差分的方法进行震源波场重建。

FWI需要匹配正演模拟数据与实际观测数据，若两者的子波不匹配，会严重影响反演精度[14，15]。在FWI中，地震子波的处理策略主要分为以下两大类。一类是不依赖子波的FWI方法，通过引入参考道消除地震子波对FWI的影响。Lee等[16]在频率域将地震数据与参考道相除，得到归一化波场用于消除地震子波的影响，但是当地震数据存在噪声时会明显降低反演精度[17，18]。Zhou 等[19]提出一种用多道平均作为参考道的策略，通过叠加可以消除噪声影响，但在参考道中仍存在零值使反演不稳定等问题。Choi 等[20]在时间域提出不依赖子波的FWI，并证实该方法的抗噪性更好，但是仍需提供精确的初始速度。另一类是在迭代过程中更新地震子波的方法，首先由Song等[21]提出。在反演迭代过程中将地震子波作为一个参数，同时反演速度与地震子波，称为震源信号的迭代反演方法(Iterative Estimation of the Source Signature，简称IES)。该方法的缺点在于若初始速度不准确，则每次迭代得到的地震子波也会存在巨大误差，最终导致反演失败。

在实际应用中最直接的获得地震子波的方法是提取直达波作为震源信号。然而，由于实际介质中传播路径的影响及透射波、反射波以及散射波等的存在，直达波并不能作为真正的地震子波[22]。本文提出一种基于波动方程重建震源子波的三维FWI方法，通过提取叠前炮集近炮检距的直达波作为波动方程求解的边界条件，重新求解波动方程，并记录震源点处的时间序列作为地震子波。该方法利用震源波场重建原理模拟震源爆炸沿地表传播的逆过程，在逆推过程中提取近炮检距直达波，避免了折射波、反射波以及潜水波等干扰。该方法只使用模型表层速度，可以有效降低对初始模型的依赖。将重建的地震子波用于三维模型及实际工区的FWI中，验证了本文算法求取地震子波的可行性与适用性。

2 方法原理

2.1 FWI方法

在数学上FWI可以定义为一种局部寻优的最优化方法，通过建立最小二乘目标函数寻找目标函数的全局最小值。定义目标函数E，表示观测数据d与模拟数据的L2范数[2]，即

(1)

式中F(m)为正演算子，其中m为模型参数。

在时间域，正演模拟数据一般通过双程波波动方程获得，实际上应该考虑波传播过程中的衰减、各向异性等因素[23]。然而，由于计算资源的限制，通常采用减少各向异性参数的个数[24]、甚至选用各向同性介质的方法，本文的正演方程为以下常密度声波方程

(2)

式中：P(x,t)为压力波场；v(x)为速度参数，对应式(1)中的m，其中x为模型空间某点的坐标；f(x,t)为震源项。

由于FWI的高度非线性，通常采用局部线性最优化方法进行迭代反演。根据牛顿迭代法，每次迭代的参数更新可表示为[25]

(3)

(4)

式中：J为Jacobi矩阵；T为模拟地震数据中的最大时间；λ(x,t)表示残差反传波场。

2.2 波动方程源波场重建子波

式(2)为常密度声波方程，在时间域可以用格林函数与震源表示该式的解

(5)

式中：ξ为震源的空间位置；τ为时间；V为体积分域。

求位移的过程可以看作震源项与格林函数在时间域的褶积。在声介质假设下，式(2)与式(5)用于模拟获得观测数据的过程，如震源激发后，波传播至检波器时可接收到直达波(图1)。

图1 波传播示意图

设直达波为dΩ，则重新构建的常密度声波方程为

(6)

式(6)为常密度声波传播方程的定解问题，与式(2)相比，式(6)中不含震源项。以地表接收到的直达波为方程求解的边界条件，并假设初始条件为零。此过程模拟震源爆炸沿地表传播的逆过程以求取地震子波，若正过程为震源项与格林函数在时间域的褶积，则求取子波的过程可表示为位移与格林函数在时间域的反褶积

(7)

式(7)为直达波逆时传播求取地震子波的积分表示式，由于整个过程是数值求解，不需要求得地震子波的解析解。在重新求解时，取近炮检距的直达波为方程求解的边界条件，避免了折射波、反射波以及潜水波等干扰。由于利用直达波为方程求解的边界条件，故式(6)中的v(x)为地表速度，只要求地表处速度接近真实速度，降低了对初始速度的依赖。

数值求解采用时间2阶、空间N阶的有限差分方法，通过保存不同层数的边界值，可用不同的震源波场重建方法求解。文中保存一层边界的直达波数据，使用Feng等[13]提出的震源波场重建方法，其原理如图2所示。

图2 波场重建原理图

以模型地表处右边界为例，黑色实心圆为模型边界，此边界在吸收边界内部，d为记录的直达波边界值。由于只记录一层直达波值，因此计算P2用2阶差分，计算P3用4阶差分，以此类推，…，计算PN/2用N阶差分。在N/2层内，用以上方法计算，超出N/2层后，计算PK用N阶差分

图3 FWI流程图

本文在子波计算与梯度求取时均利用了震源波场重建方法(图3)，前者利用直达波逆时回推得到地震子波，后者以计算代替存储减少I/O的消耗。

3 数值试验

3.1 模型测试

采用三维SEG/EAGE推覆体速度模型(图4)，其中初始速度(图4b)由真实速度(图4a)经过一定平滑后得到。正演模拟所用子波为雷克子波(见图7a)，正演模拟采用时间2阶、空间10阶有限差分算法。首先，输入真实速度体(图4a)，通过三维正演模拟得到叠前炮集。正演模拟仅为了得到沿地表传播的直达波，因此并不考虑覆盖次数以及炮检距大小。为了避免折射波、潜水波等干扰，通常只考虑近炮检距直达波。图5为震源点位于(0，0，0)处的正演模拟记录。

截取近炮检距信噪比较高的直达波进行计算，以记录所有炮点得到的震源子波(图6)。图7为重建子波与雷克子波。由图可见，雷克子波与重建子波的频谱几乎一致(图7b)，但两者在相位上存在差异(图7a)。因此对重建子波做一步相位调整，以使重建子波与雷克子波的相位一致，得到相位校正后的子波(图8)。可见重建子波与输入的雷克子波几乎只存在相位差别，经过相位校正后，两者形态几乎一致。

图4 三维SEG/EAGE推覆体模型

以图左上角自定义三维坐标系为依据，x、y方向网格点数均为401，z方向网格点数为121，x、y、z方向网格尺寸均为10m。震源和检波器都分布在地表处，共121炮，第一炮位于(0，0，0)处，第一个检波点也位于(0，0，0)处。x、y方向的炮间距均为400m，x、y方向的检波点间距均为100m，炮检距为 1000m。地震记录的时间采样间隔为0.6ms，时间采样点数为1600

图5 震源点位于(0，0，0)处的正演模拟记录

图6 重建的三维地震子波

以重建的三维地震子波作为正演模拟子波进行三维FWI测试，测试模型为三维SEG/EAGE推覆体模型(图4)。观测地震数据由校正后的雷克子波(图8中黑线所示)作为震源子波通过正演模拟获得，模拟地震数据由校正后的重建三维地震子波(图8中红线所示)通过正演模拟获得。 震源和检波器都分布在地表，共629炮，第一炮位于(0，0，0)处，第一个检波点也位于(0，0，0)处。x、y方向的炮间距均为160m，x、y方向的检波点间距均为10m，炮检距为1000m。地震记录的时间采样间隔为0.6ms，时间采样点数为1600。数值模拟采用时间2阶、空间10阶有限差分算法，三个方向的空间采样网格尺寸均为10m。

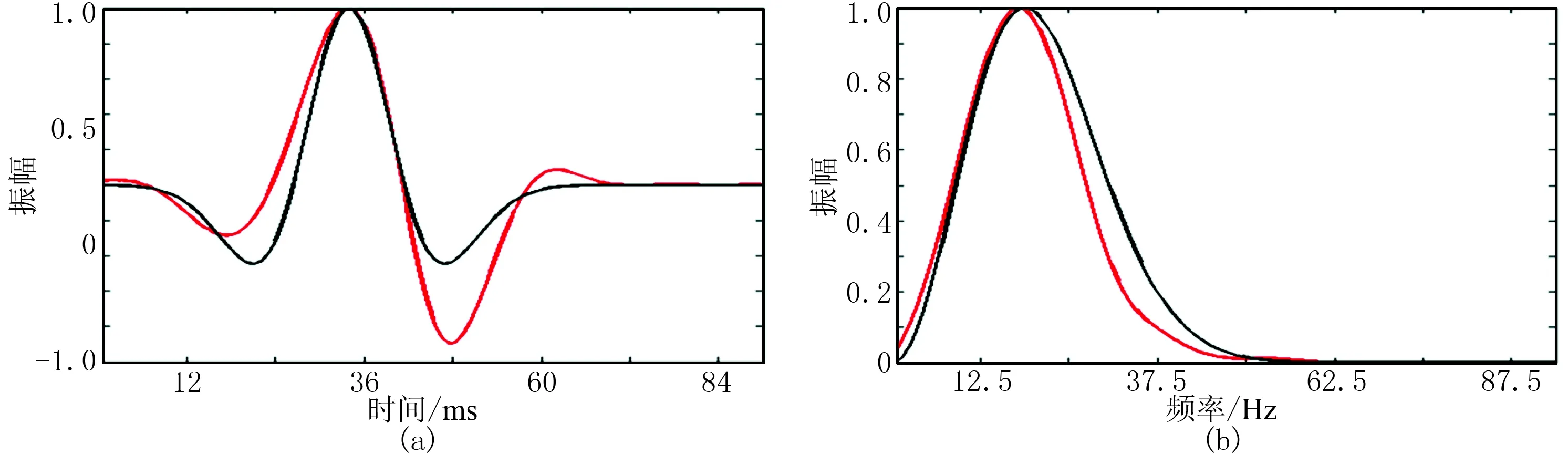
图7 重建子波与雷克子波及其频谱

图8 相位校正后的子波黑线为雷克子波，红线为重建子波

图9为不同迭代次数的三维SEG/EAGE推覆体模型的FWI结果。由图9可见，随着迭代次数的增大，构造细节成像越来越清晰，如明显恢复了z=0.6km处切片的河道(蓝色椭圆内)细节。图10为实际速度与FWI速度对比，图11为河道处单道速度对比。由图可见，FWI速度接近真实速度，特别在河道处(黄色虚线)的FWI结果更加可靠。

图9 不同迭代次数的三维SEG/EAGE推覆体模型的FWI结果

图10 真实速度(a)与FWI速度(b)对比

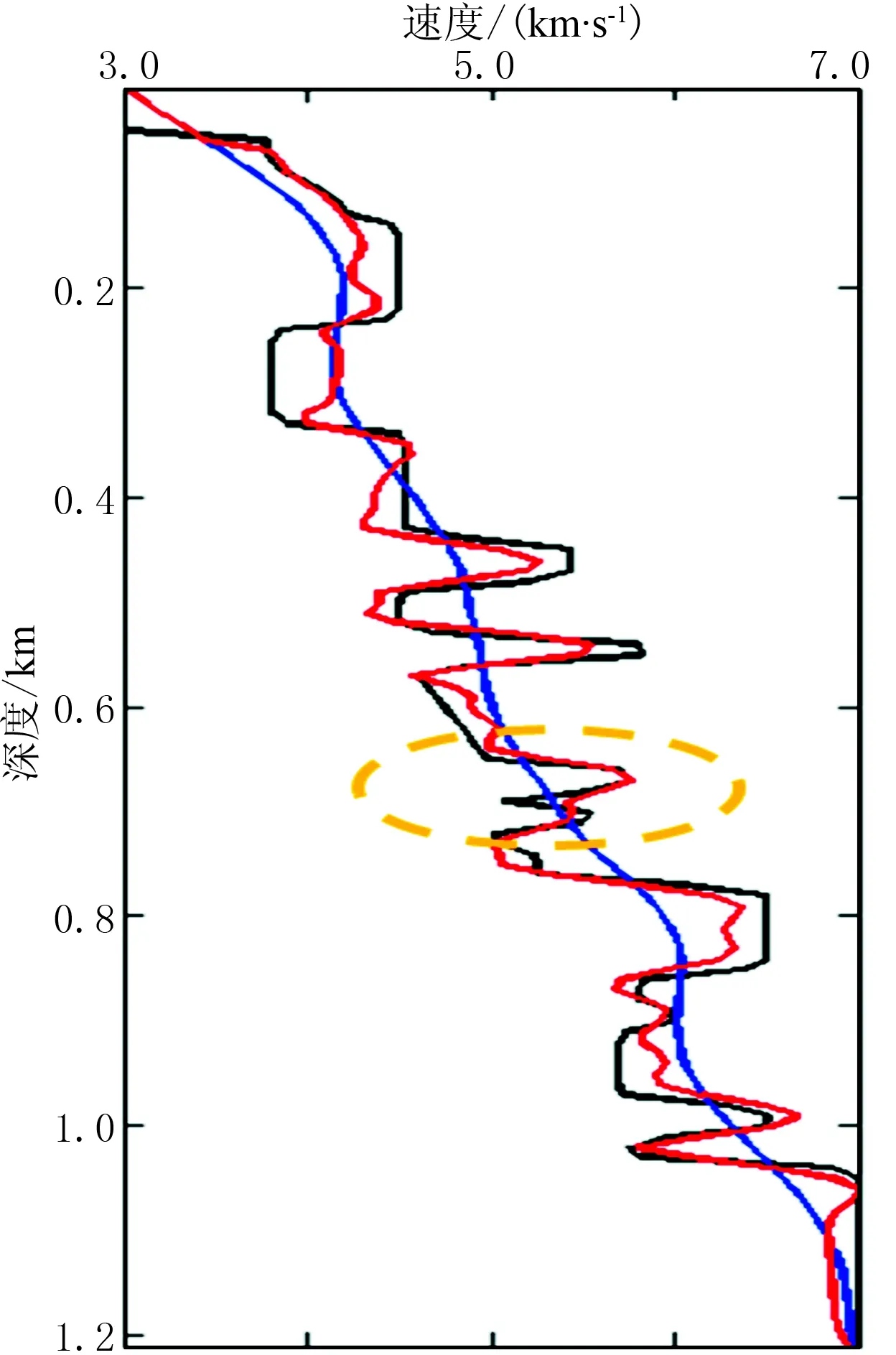
图11 河道处单道速度对比

4 实际应用

选取中国东部三维M区的叠前地震资料进行试算。该区地表起伏平缓，地震资料信噪比较高，所用的初始速度场由偏移速度分析所得，且初始速度场的表层速度接近真实速度场的表层速度，满足本文算法的假设。兼顾计算机与三维叠前FWI计算量与数据量的需求，选取较小块的、观测系统相对规范的、有井位验证的三维区块。所选区块共882炮数据，炮检距为 3000m，所获得的叠前资料做过地表一致性校正等处理。截取近炮检距处信噪比较高的直达波进行计算，记录所有炮点得到的震源子波(图12)，可见拟合得到的最终震源子波接近最小相位子波。

用实际资料重建的三维地震子波(图12)对该区882炮数据进行三维FWI测试，图13为迭代17次得到的速度连井剖面， 该剖面为反演三维速度场中抽取的一条过井剖面。由图可见，反演速度与井曲线吻合较好。图14为观测地震记录与模拟地震记录对比。由图可见，观测记录(图14a)与模拟记录(图14b)在波形、相位等方面均有较好的对应。

图12 实际资料重建的三维地震子波

图13 迭代17次得到的速度连井剖面

图14 观测地震记录(a)与模拟地震记录(b)对比

5 结束语

本文提出一种基于波动方程重建震源子波的三维FWI方法。应用波动方程的求解理论，将地表接收到的直达波作为波动方程求解的边界条件，以地表速度作为波动方程的速度参数，通过重新求解波动方程得到地震子波。该方法模拟震源爆炸沿地表传播的逆过程，利用叠前地震资料近炮检距直达波信息，避免了折射波、反射波以及潜水波等干扰。并且该方法只假定地表处速度接近真实速度，降低了对初始速度的依赖。

利用三维SEG/EAGE推覆体模型进行测试，对每个炮点都可以求取对应的地震子波，多个炮点拟合后得到的地震子波与初始输入的雷克子波存在相位差异，但振幅谱无明显差异，经过相位校正后即可进行三维FWI，并可得到较为准确的速度参数。利用实际资料求得的地震子波接近零相位子波，可直接用于FWI反演，通过与连井曲线对比，证明了本文算法的可行性与适用性。尚需指出，本文的算法研究是在假定地表速度接近真实速度的基础上开展的，并且只考虑了速度因素，而影响地震波传播的因素很多，如衰减、各向异性等，需考虑这些因素才能更好地模拟震源爆炸沿地表传播的逆过程，从而求得更准确的地震子波。因此文中算法只适用于地表起伏平缓的地区，对于地表起伏剧烈的地区不一定适用。

[1] Lailly P.The seismic inverse problem as a sequence of before stack migrations.Conference on Inverse Scattering:Theory and Application.Society for Industrial and Applied Mathematics,Philadelphia,PA,1983,206-220.

[2] Tarantola A.Inversion of seismic reflection data in the acoustic approximation.Geophysics,1984,49(8):1259-1266.

[3] 王毓玮,董良国,黄超等.降低弹性波全波形反演强烈非线性的分步反演策略.石油地球物理勘探,2016,51(2):288-294.

Wang Yuwei,Dong Liangguo,Huang Chao et al.A multi-step strategy for mitigating severe nonlinearity in elastic full-waveform inversion.OGP,2016,51(2):288-294.

[4] 李志晔,李振春,刘玉金等.基于波场分离的层析波形反演方法.石油地球物理勘探,2016,51(2):295-300.

Li Zhiye,Li Zhenchun,Liu Yujin et al.Tomographic waveform inversion with wave-field decomposition.OGP,2016,51(2):295-300.

[5] Virieux J,Operto S.An overview of full-waveform inversion in exploration geophysics.Geophysics,2009,74(6):WCC1-WCC26.

[6] 付继有,李振春,杨国权等.声介质波动方程反射旅行时反演方法.石油地球物理勘探,2015,50(6):1134-1140.

Fu Jiyou,Li Zhenchun,Yang Guoquan et al.Wave equation reflection travel-time inversion in acoustic media.OGP,2015,50(6):1134-1140.

[7] Maurer H,Greenhalgh S,Latzel S.Frequency and spatial sampling strategies for crosshole seismic waveform spectral inversion experiments.Geophysics,2009,74(6):C79-C89.

[8] Krebs J R,Anderson J E,Hinkley D et al.Fast full-wavefield seismic inversion using encoded sources.Geophysics,2009,74(6):C177-C188.

[9] Habashy T,Abubakar A,Pan G et al.Source-receiver compression scheme for full-waveform seismic inversion.Geophysics,2011,76(4):R95-R108.

[10] Ben-Hadj-Ali H,Operto S,Virieux J.An efficient frequency-domain full waveform inversion method using simultaneous encoded sources.Geophysics,2011,76(4):R109-R124.

[11] Li X,Aravkin A,van Leeuwen T et al.Fast randomized full-waveform inversion with compressive sensing.Geophysics,2012,77(3):A13-A17.

[12] Gauthier O,Virieux J,Tarantola A.Two-dimensional nonlinear inversion of seismic waveforms:Numerical results.Geophysics,1986,51(7):1387-1403.

[13] Feng Bo,Wang Huazhong,Tian Lixin et al.A strategy for source wavefield reconstruction in reverse time migration.SEG Technical Program Expanded Abstracts,2011,20:3164-3168.

[14] 陈乐寿,王光锷.大地电磁测深法.北京:地质出版社,1984.

[15] 杨培杰,印兴耀.地震子波提取方法综述.石油地球物理勘探,2008,43(1):123-128.

Yang Peijie,Yin Xingyao.Summary of seismic wavelet pick-up.OGP,2008,43(1):123-128.

[16] Lee K H,Kim H J.Source-independent full-waveform inversion of seismic data.Geophysics,2003,68(6):2010-2015.

[17] Xu K,Greenhalgh S A,Wang M Y.Comparison of source-independent methods of elastic waveform inversion.Geophysics,2006,71(6):R91-R100.

[18] Choi Y,Min D J.Source-independent elastic waveform inversion using a logarithmic wavefield.Journal of Applied Geophysics,2012,76:13-22.

[19] Zhou B,Greenhalgh S A.Crosshole seismic inversion with normalized full-waveform amplitude data.Geophysics,2003,68(4):1320-1330.

[20] Choi Y,Alkhalifah T.Source-independent time-domain waveform inversion using convolved wavefields:Application to the encoded multisource waveform inversion.Geophysics,2011,76(5):R125-R134.

[21] Song Z M,Williamson P R,Pratt R G.Frequency-domain acoustic-wave modeling and inversion of crosshole data:Part Ⅱ-Inversion method,synthetic experiments and real-data results.Geophysics,1995,60(3):796-809.

[22] 敖瑞德,董良国,迟本鑫.不依赖子波、基于包络的FWI初始模型建立方法研究.地球物理学报,2015,58(6):1998-2010.

Ao Ruide,Dong Liangguo,Chi Benxin.Source-independent envelope-based FWI to build an initial model.Chinese Journal of Geophysics,2015,58(6):1998-2010.

[23] Zhou H,Amundsen L,Zhang G.Fundamental issues in full waveform inversion.SEG Technical Program Expanded Abstracts,2012,31.

[24] Warner M,Ratcliffe A,Nangoo T et al.Anisotropic 3D full-waveform inversion.Geophysics,2013,78(2):R59-R80.

[25] Ma Y,Hale D.Quasi-Newton full-waveform inversion with a projected Hessian matrix.Geophysics,2012,77(5):R207-R216.

*山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院，266580。Email:lzy09017216@163.com

本文于2016年11月28日收到，最终修改稿于2017年9月6日收到。

本项研究受国家“973”重大专项(2013CB228604)和国家自然科学基金—石油化工基金联合重点项目(U1562215)联合资助。

1000-7210(2017)06-1200-08

梁展源，吴国忱，王玉梅.基于波动方程重建震源子波的三维全波形反演.石油地球物理勘探，2017,52(6):1200-1207.

P631

A

10.13810/j.cnki.issn.1000-7210.2017.06.010

(本文编辑：刘勇)

梁展源 博士研究生，1989年生；分别于2013、2016年获中国石油大学(华东)地球物理学专业学士学位、地质资源与地质工程专业硕士学位； 目前在中国石油大学(华东)地球科学与技术学院攻读地质资源与地质工程专业博士学位，研究方向为应用地球物理正、反演方法。