基于总体最小二乘改进的SDFT三相交流电频率估计算法

刘 勇 王 开 刘 航 沈佳佳 裴文江 夏亦犁

(东南大学信息科学与工程学院, 南京 210096)

基于总体最小二乘改进的SDFT三相交流电频率估计算法

刘 勇 王 开 刘 航 沈佳佳 裴文江 夏亦犁

(东南大学信息科学与工程学院, 南京 210096)

为了解决SDFT算法在含有噪声、谐波或突发干扰的电力网络中电压信号基频分量三点关系式不严格成立的问题,引入总体最小二乘算法(TLS-SDFT)进行改进．TLS-SDFT算法采用滑动窗截取的多个DFT基频分量样本点来扩展SDFT算法的三点关系式,引入扰动矩阵,并通过对系数矩阵进行奇异值分解,使扰动矩阵具有最小Frobenious范数,得到改进的频率估计值．由于系数矩阵结构的特殊性,该算法的额外复杂度为窗长的线性函数．仿真结果表明,在高斯白噪声干扰下,改进算法的估计偏差和均方误差远低于原SDFT算法．在高次谐波干扰、信号参数突变以及变电站实测环境下,改进算法的频率追踪精确度均有明显提升．

频率估计;总体最小二乘;离散傅里叶变换;参数估计

在电力系统中,系统频率是控制电力网络负荷不平衡的一个关键参数,可决定非线性负载造成的谐波电流干扰等．精确的频率估计算法对维持电力网络和常用电力设备的稳定性至关重要．将电网设备电压信号视为纯正弦信号,则信号的2次过零时间间隔为系统频率的一个重要参考[1]．

被测信号极易被噪声或其他信号干扰,国内外研究者们已提出多种针对不同场景下的频率估计算法,包括锁相环算法[2]、陷波器[3]、最小均方算法及其变体[1,4]、自适应滤波器[5]、Kalman滤波[6]、泰勒展开系列算法[7]、迭代算法[8]等．

基于DFT的频率估计算法在电力系统中已有广泛应用．为克服有限长DFT频谱采样性对算法性能的影响,通常采用窗函数来降低频谱泄露,并通过插值算法来降低栅栏效应带来的误差[9]．为了进一步降低DFT算法复杂度、减少其对系统同步采样的依赖性,Yang等[1,10]利用连续样点的DFT基频分量之间的关系,研究了高次谐波和系统频偏情况下的精确估计算法．

在SDFT算法的基础上,本文推导了TLS-SDFT算法原理,并验证了其在电力系统中的抗噪性能及鲁棒性．

1 SDFT算法

本文主要考虑电力系统信号的频偏估计问题．理想条件下,信号模型可表示为

x(n)=Xcos(wnΔT+φ)

(1)

式中,x(n)为离散电压信号,其中n为离散时刻;X为幅值;φ为初始相位;ΔT为采样间隔;w=2πf0为数字角频率,其中f0为系统标准频率．对于采样频率为fs的系统,ΔT=1/fs,通常fs=Nf0,其中,N为周期采样点数．

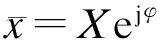
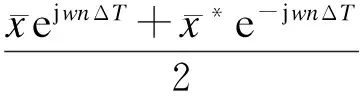
(2)

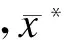
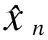
(3)

考虑系统频偏Δf,即w=2π(f0+Δf),合并式(2)和(3),得

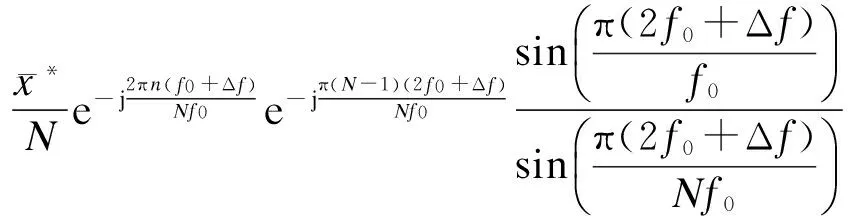
(4)

定义与n相关的变量bn和cn分别表示式(4)右边第1项和第2项,令

则bn和cn有如下递推关系:

bn=abn-1,cn=a-1cn-1

(5)

3个连续时刻的DFT基频分量可表示为

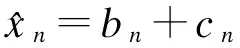
(6)

令

(7)

进一步,可得到基频分量三点关系式为

(8)

由此可得r的估计值为

(9)

进一步,得到f的估计值为

(10)

式中,R(·)为复数的取实部运算．

2 TLS-SDFT算法

SDFT频率估计算法在理论上是正确的．然而,当信号受到噪声或高次谐波干扰时,算法性能会下降,原因是受干扰的信号会使式(8)不再严格成立,且r=a+a-1为复数．尽管SDFT算法使用R(·)运算来降低这些干扰,但效果并不理想．为了克服这一缺陷,本节将引入总体最小二乘算法来降低噪声、谐波等干扰的影响．

式(8)对于任意时刻n都成立,假设系统参数在一个短时间窗L内时不变[11],可得到扩展的基频分量关系式为

(11)

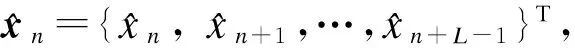
(12)

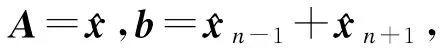
Ar=b

(13)

设A,b的误差向量分别为E,e，则

(A+E)r=b+e

(14)

式(14)的最小二乘解考虑了系数的总体误差,故将改进的算法称为TLS-SDFT算法．

式(14)可等价写为

(15)

令

则式(15)可写为

(B+D)z=0

(16)

求解方程(14)的TLS算法可以描述为求解如下最优化问题:

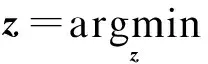
(17)

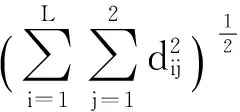
TLS算法的基本思想是使来自于A和b的扰动噪声最小．具体步骤为:求解具有最小范数的扰动矩阵D∈RL×2,使得B+D是非满秩的(如果满秩,则只有平凡解z=0)．通常,使用SVD来解决这一问题,令

B=UΣVH

(18)

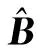
(19)

式中,Σ1的第1个奇异值与矩阵B的第1个奇异值相同,其他奇异值为0．

本文引入的是TLS算法中的一个特例．常规TLS算法的系数矩阵为m×s维,矩阵B的有效秩为p(即z中独立未知数的个数为p),且s≥p≥1．此处,由式(12)可知,s=p=1．

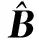
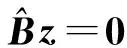
(20)

不难证明

(21)

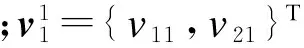
根据最小二乘原理,求方程(20)的最小二乘解等价于使如下代价函数最小化:

(22)

(23)

可将代价函数记为f(z)=zHSz,由∂f(z)/∂z=0化简得到

Sz=αe

(24)

式中,e={1,0}T;归一化常数α的选择应使参数向量z中的第1个元素为1．

(25)

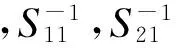
将其代入式(10),即可得到频率的估计值为

(26)

3 仿真与分析

为了验证TLS-SDFT算法的性能,利用MATLAB软件对电力系统中常见的几种信号模型[13]进行仿真．仿真过程中,设定f0=50 Hz,fs=1 600 Hz,L=15,所加噪声均为高斯白噪声．

在电力系统的噪声环境下,TLS-SDFT算法和SDFT算法的估计偏差和均方误差如图1所示．图中,加入噪声的输入信号模型为x(n)=cos(2πfn+0.3π)+u(n),其中,u(n)为高斯白噪声,系统实际频率f=f0+Δf=50.5 Hz,一共进行了1 000次独立实验．由图可知,TLS-SDFT算法的估计偏差较SDFT算法降低20 dB,均方误差降低30 dB．

图2给出了受谐波干扰的电力系统环境下2种算法的频率追踪精确度对比．系统实际频率为49.8 Hz,截取0.5 s的采样数据,输入信号的模型为x(n)=cos(2πfn+0.3π)+0.2cos(6πfn-0.1π)．由于原SDFT算法在理论上并未考虑高次

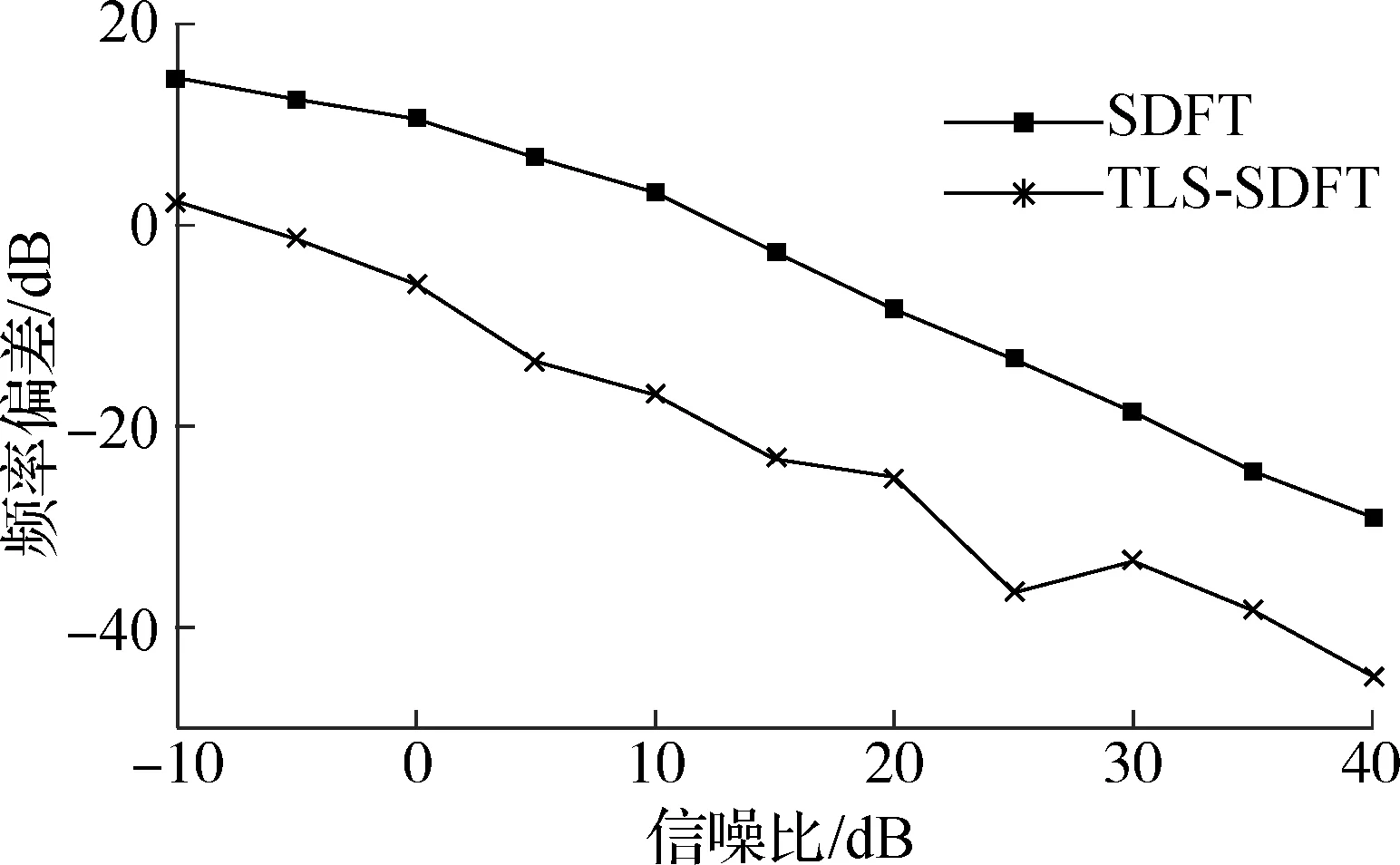
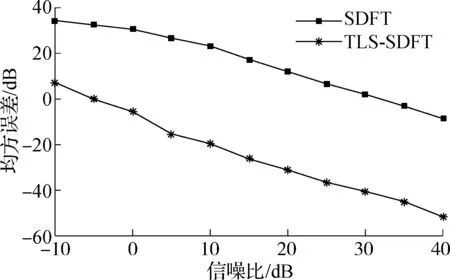
图1噪声环境下2种算法性能比较

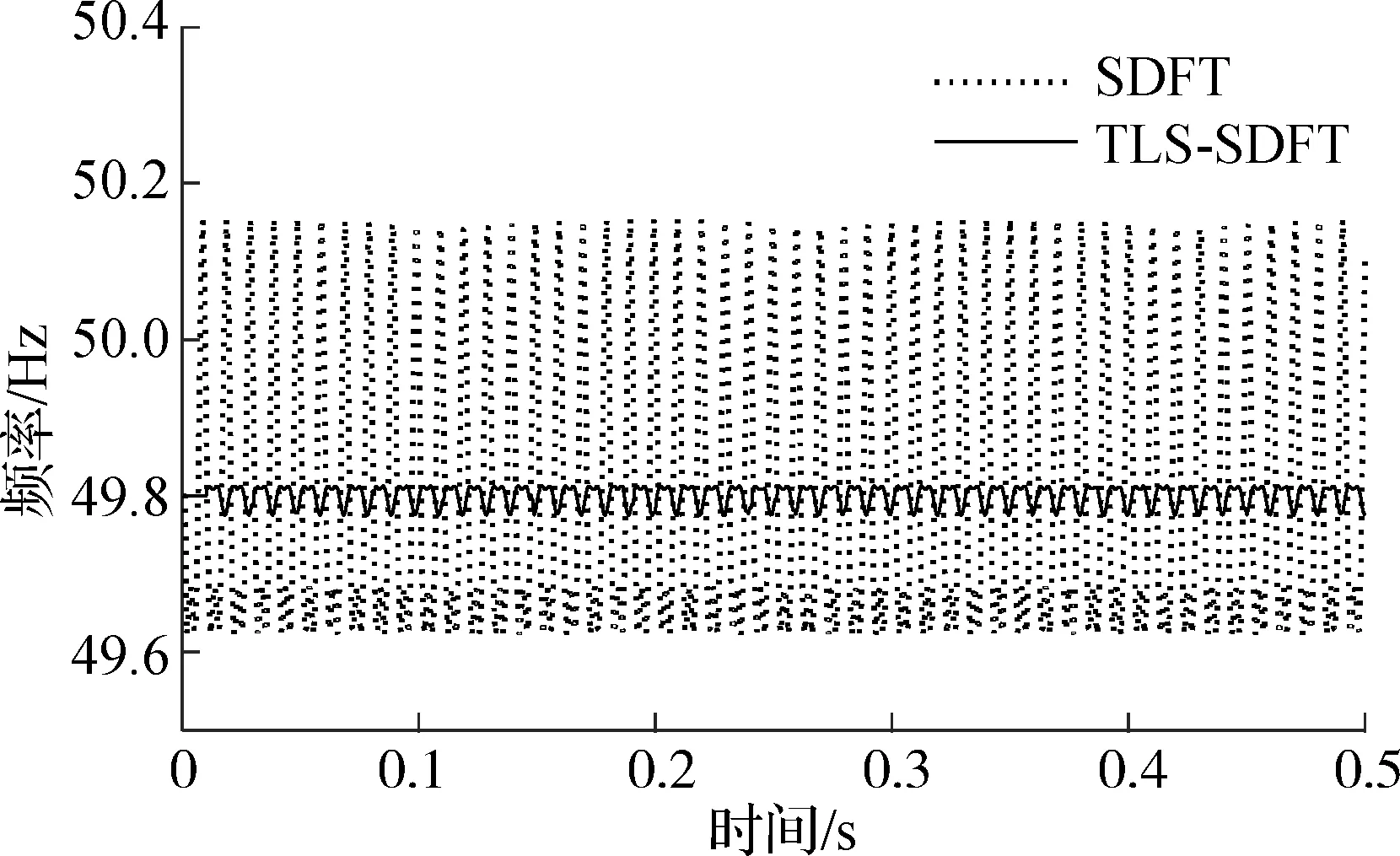
谐波的干扰,三次谐波信号的存在使得DFT基频分量的三点关系误差较大．而TLS-SDFT算法通过观测窗弱化了这一误差,从而提高了算法的抗谐波干扰能力．由图2可知,TLS-SDFT算法的估计误差明显小于SDFT算法．SDFT算法和TLS-SDFT算法的最大估计误差分别为0.354 5和0.028 4 Hz,后者降低了一个数量级．

在电力系统中,某些设备故障或开关操作会引起系统电压的幅值、相位等参数发生一定程度的峭变．仿真中,系统实际频率设定为50.1 Hz,输入信号模型为x(n)=cos(2πfn+0.1π)．图3给出了2种算法在幅值突变10%、相位突变0.1π

时的频率追踪精确度．由图可知,2种算法的估计结果都会出现波动,但对相位干扰更为敏感．产生这一现象的原因在于,对信号模型整体而言,相位的导数即为频率,突变的相位意味着频率实际值波动变大,从而导致2种算法的追踪性能变差．此外,算法的响应时间与所取的观测窗长L有关,L越大,响应时间越长,估计误差越小．因此,为了较好地在二者之间取得折中,通常取L=5．在这一观测窗长下,TLS-SDFT算法具有很好的估计性能,在噪声和谐波干扰环境下具有较强的鲁棒性．

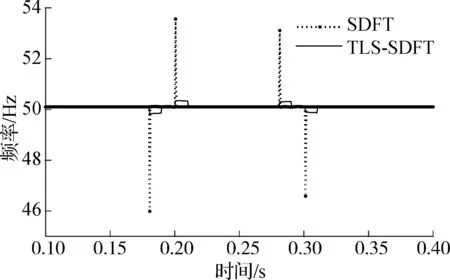
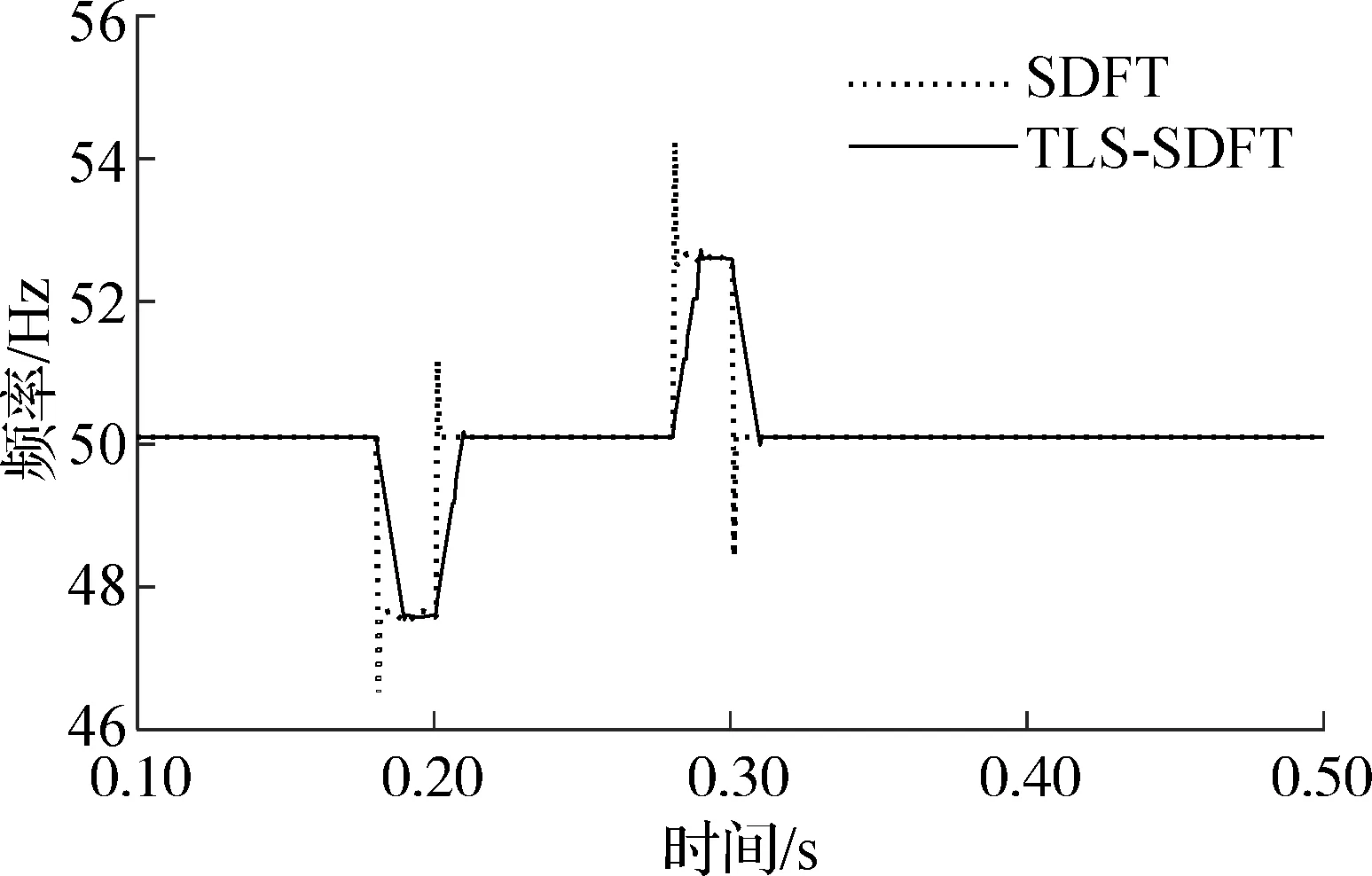
图3系统参数峭变场景下的频率追踪精确度对比

在某些故障或负载损耗的场合下,电力系统的负载平衡遭到破坏,导致波形的幅值、频率受到不同程度的调制,将系统实际频率设定为49.9 Hz．

对于幅值调制的场景,信号模型为x(n)=(1+0.2cos(2πfn))cos(2πfn+0.3π)．L=15时频率追踪精确度如图4(a)所示．由图可知,TLS-SDFT算法的最大估计误差(2.7 mHz)明显低于SDFT算法．

对于频率调制的场景,信号模型为

(27)

对应的频率函数为

(28)

式中,t表示连续时间．

在这种动态环境下,由图4(b)可知,TLS-SDFT算法具有更精确的估计结果,并且能够动态追踪信号频率的变化．

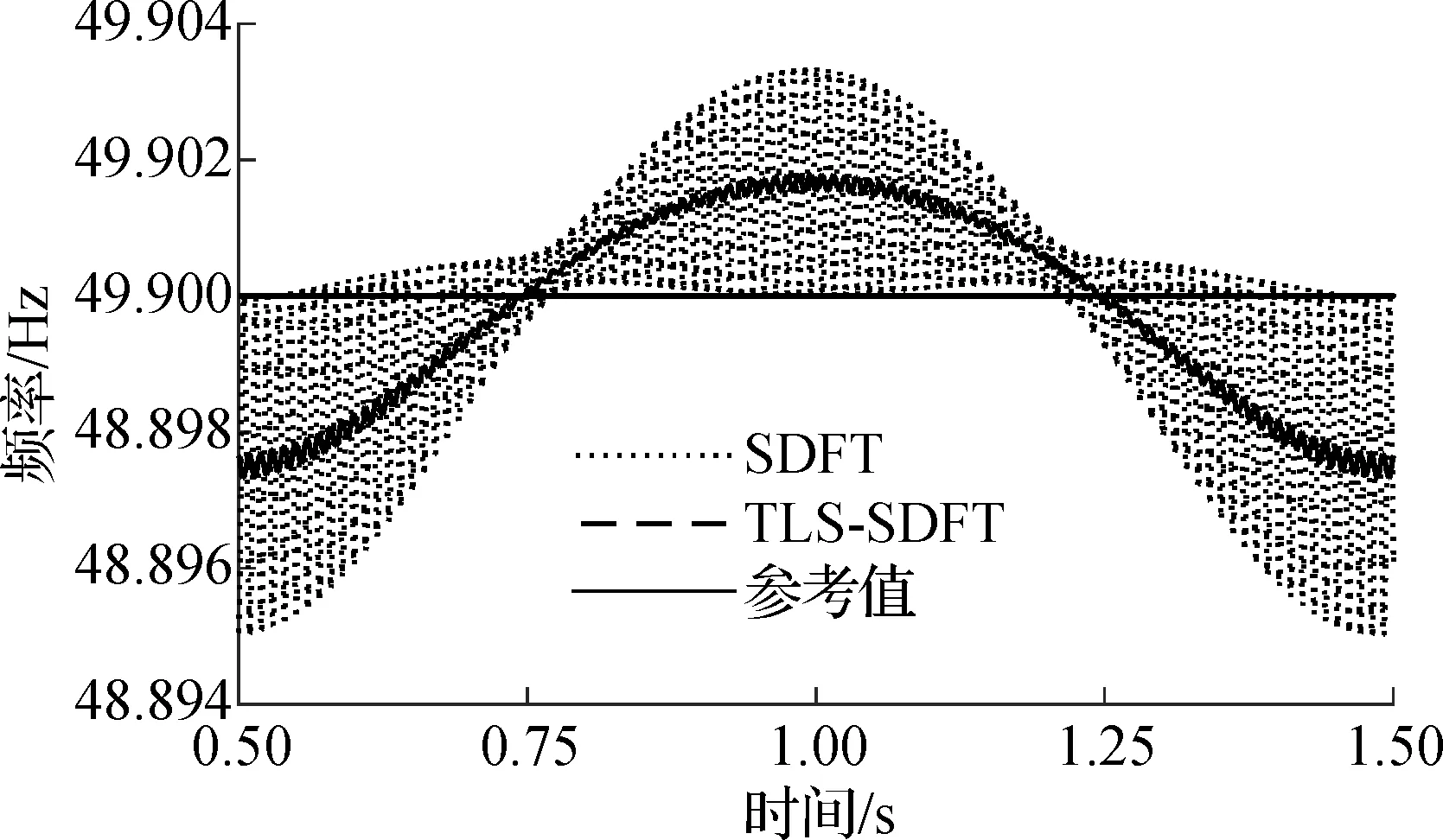
(a) 幅值调制

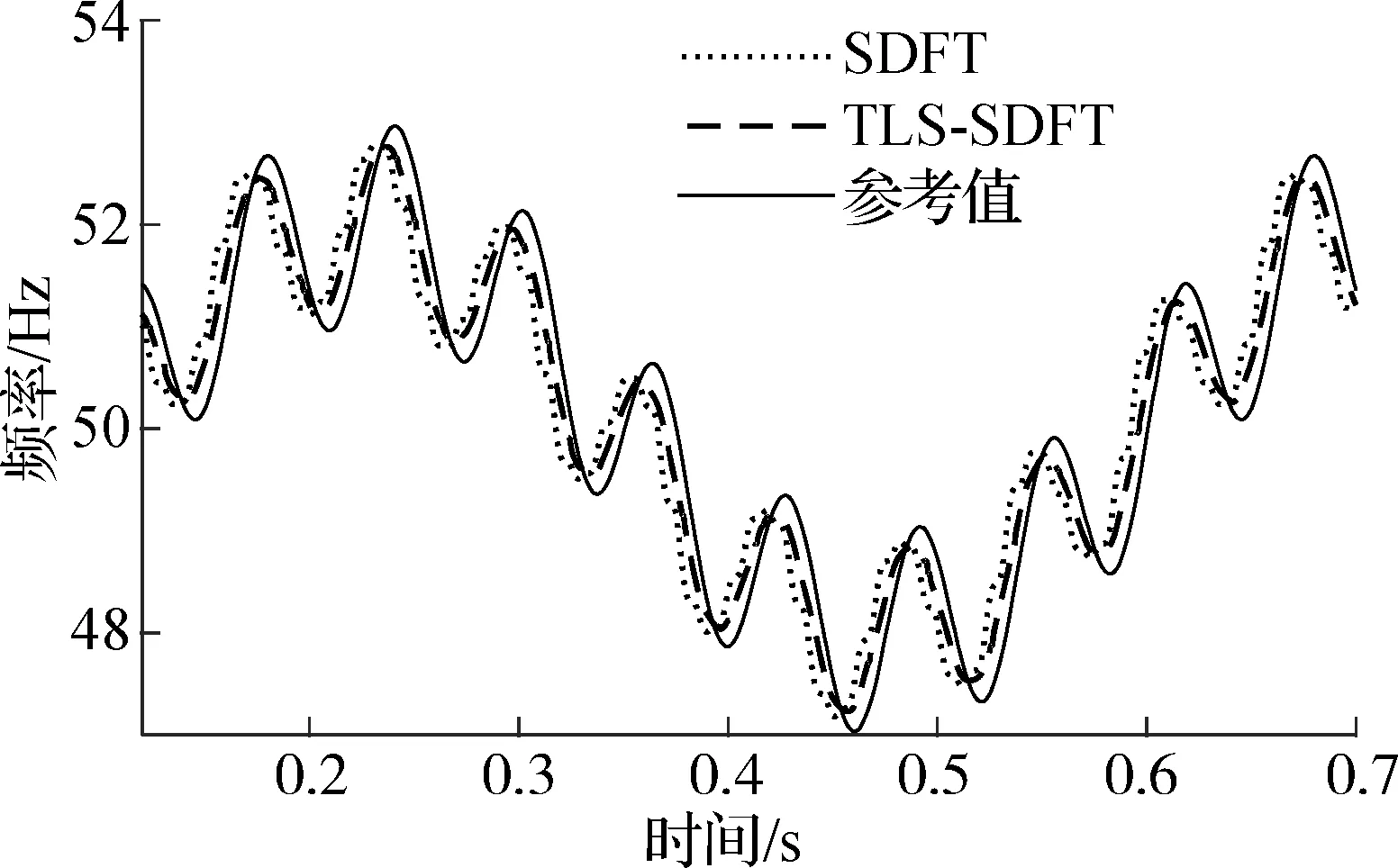
(b) 频率调制

当频率以1和-1 Hz/s增加时，2种算法的频率追踪结果见图5．图5(a)和(b)的信号模型分别为x(n)=cos(2π(f+0.5n)n+0.3π)和x(n)=cos(2π(f-0.5n)n+0.3π)．

由图5可以看出,TLS-SDFT算法的估计结果较SDFT算法更接近参考值,且没有明显波动．在这2种信号模型下,2种算法的估计值均位于参考值的同一侧．究其原因在于,如式(11)所示,本文采用了前向预测窗模型,导致当前时刻频率估计值与时刻n前一个、后L+1个信号的采样值有关,故2种算法的估计结果都体现出一定的超前性．

变电站电压信号实测环境下2种算法的性能对比见图6．该单相接地电压信号来自于某110 kV变电站,采样频率为1 kHz．表1列出了0.3 s内2种算法估计值的最大偏差和方差．结果表明,TLS-SDFT算法具有更好的鲁棒性．

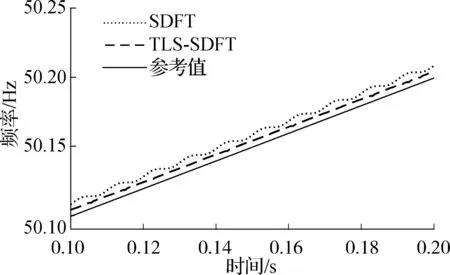
(a) 斜率为1 Hz/s

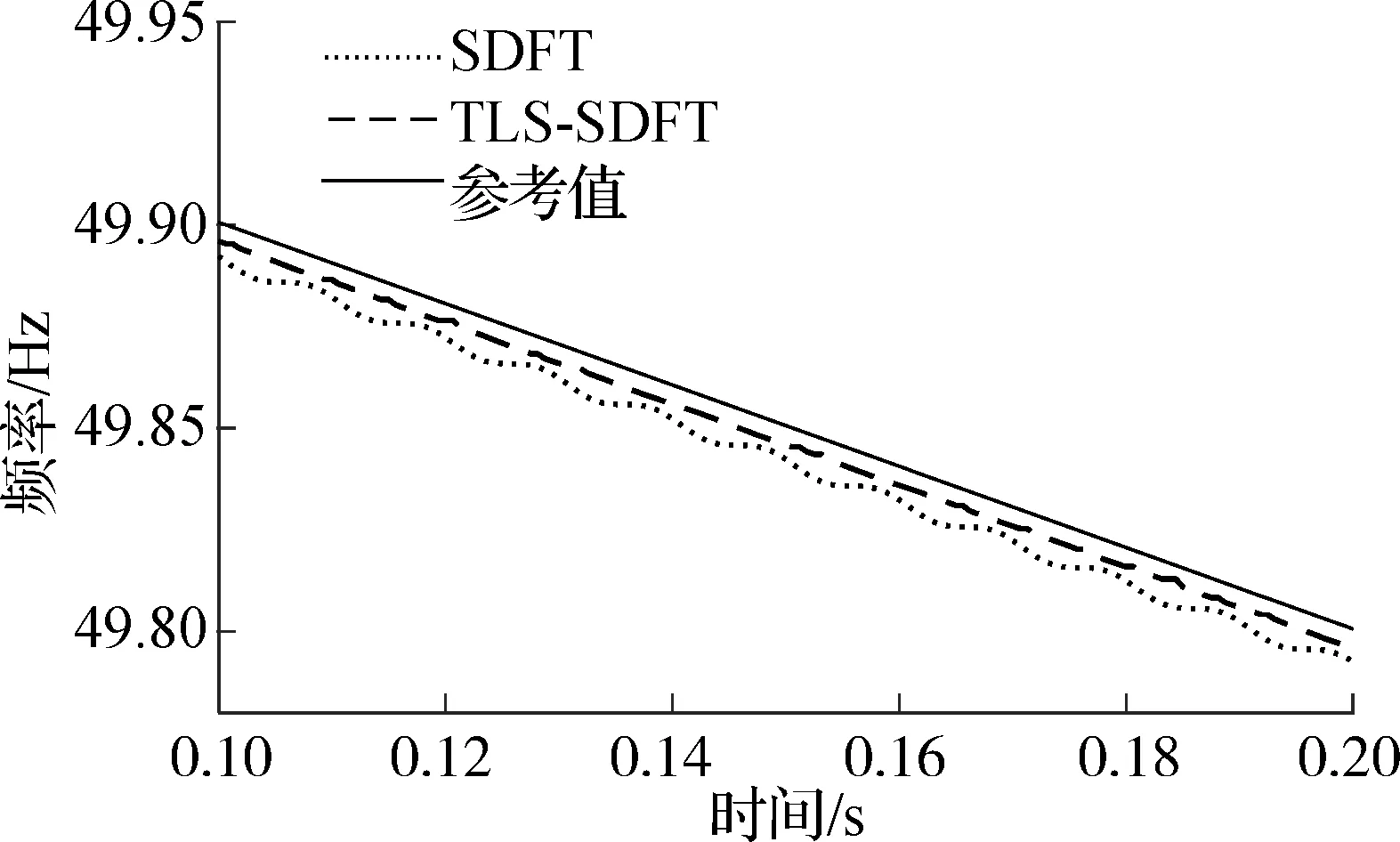
(b) 斜率为-1 Hz/s

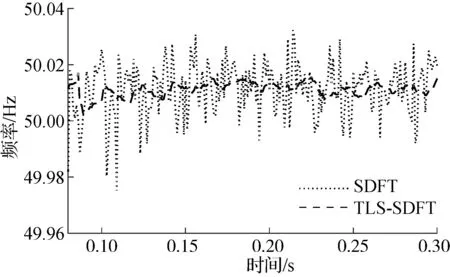
图6 变电站实测数据片段算法性能比较

算法最大偏差/Hz方差/Hz2SDFT1.38720.0168TLS-SDFT0.25540.0037

4 结论

1) TLS-SDFT算法通过在扩展的信号基频分量三点关系式中引入扰动矩阵D,并对时域窗截取的系数矩阵进行SVD分解求得最优解,额外复杂度为Ο(L)．

2) 在高斯噪声、谐波、系统参数动态变化等仿真环境下,TLS-SDFT算法都具有良好的精确度和鲁棒性．在变电站的实测数据下,TLS-SDFT算法的最大估计偏差、方差均低于SDFT算法．

3) 在某些系统参数发生突变的场景下,受时域窗的影响,TLS-SDFT算法的动态反应能力不如SDFT算法．后续工作拟在不牺牲精确度的前提下,进一步降低窗长的选择,并降低复杂度．

)

[1] Yang J Z, Liu C W. A precise calculation of power system frequency and phasor [J].IEEETransactionsonPowerDelivery, 2000,15(2): 494-499. DOI: 10.1109/61.852974.

[2] Karimi-Ghartemani M, Ooi B T, Bakhshai A. Application of enhanced phase-locked loop system to the computation of synchrophasors [J].IEEETransactionsonPowerDelivery, 2011,26(1): 22-32.DOI:10.1109/tpwrd.2010.2064341.

[3] Mojiri M, Karimi-Ghartemani M, Bakhshai A. Estimation of power system frequency using an adaptive notch filter [J].IEEETransactionsonInstrumentationandMeasurement, 2007,56(6): 2470-2477. DOI:10.1109/tim.2007.908631.

[4] Abdollahi A, Matinfar F. Frequency estimation: A least-squares new approach [J].IEEETransactionsonPowerDelivery, 2011,26(2): 790-798. DOI:10.1109/tpwrd.2010.2090177.

[5] Xia Y, Douglas S C, Mandic D P. Adaptive frequency estimation in smart grid applications: Exploiting noncircularity and widely linear adaptive estimators [J].IEEESignalProcessingMagazine, 2012,29(5): 44-54. DOI:10.1109/msp.2012.2183689.

[6] Routray A, Pradhan A K, Rao K P. A novel Kalman filter for frequency estimation of distorted signals in power systems[J].IEEETransactionsonInstrumentationandMeasurement, 2002,51(3): 469-479. DOI:10.1109/tim.2002.1017717.

[7] Ren J, Kezunovic M. A hybrid method for power system frequency estimation [J].IEEETransactionsonPowerDelivery, 2012,27(3): 1252-1259. DOI:10.1109/tpwrd.2012.2196770.

[8] Dash P K, Hasan S. A fast recursive algorithm for the estimation of frequency, amplitude, and phase of noisy sinusoid [J].IEEETransactionsonIndustrialElectronics, 2011,58(10): 4847-4856. DOI:10.1109/tie.2011.2119450.

[9] Wen H, Guo S, Teng Z, et al. Frequency estimation of distorted and noisy signals in power systems by FFT-based approach [J].IEEETransactionsonPowerSystems, 2014,29(2): 765-774. DOI:10.1109/tpwrs.2013.2283273.

[10] Yang J Z, Liu C W. A precise calculation of power system frequency [J].IEEETransactionsonPowerDelivery, 2001,16(3): 361-366. DOI:10.1109/61.924811.

[11] Xia Y, He Y, Wang K, et al. A complex least squares enhanced smart DFT technique for power system frequency estimation [J].IEEETransactionsonPowerDelivery, 2017,32(3): 1270-1278. DOI:10.1109/tpwrd.2015.2418778.

[12] Anderson E, Bai Z, Bischof C, et al.LAPACKusers’guide[M]. Philadelphia, PA,USA:SIAM, 1999: 20-25.

[13] Martin K E. Synchrophasor standards development-IEEE C37. 118 & IEC 61850 [C]//2011 44thHawaiiInternationalConferenceonSystemSciences(HICSS). IEEE, Hawaii, USA, 2011: 1-8. DOI:10.1109/hicss.2011.393.

ImprovedSDFTalgorithmbasedontotalleastsquaresforfrequencyestimationinthree-phasepowersystem

Liu Yong Wang Kai Liu Hang Shen Jiajia Pei Wenjiang Xia Yili

(School of Information Science and Engineering, Southeast University, Nanjing 210096, China)

In the smart discrete Fourier transform(SDFT)algorithm, the underlying relationship among the three consecutive fundamental components of the voltages does not hold when the three-phase power system is contaminated by noises, harmonics, or encountered with sudden interrupts. To solve this problem, a total least squares SDFT(TLS-SDFT)algorithm is put forward. In the proposed algorithm,the original three point relation formula in the SDFT algorithm is extended based on the multiple DFT fundamental observations obtained by sliding windows.A perturbation matrix is introduced. The coefficient matrix is singular value decomposed to minimize the Frobenious norm of the perturbation matrix, and then the estimated frequency is improved. Due to the special structure of the coefficient matrix, the additional complexity of the proposed algorithm is a linear function with the length of the sliding window. The simulation results show that the estimation bias and the mean square error of the proposed algorithm are much smaller than those of the original SDFT algorithm under the interference of Gauss white noise. The frequency tracking accuracy of the proposed algorithm is obviously improved under the conditions of high harmonic interference, signal parameter mutation and real substation measurement.

frequency estimation; total least squares; smart discrete Fourier transform;parameter estimation

10.3969/j.issn.1001-0505.2017.06.008

TM935.1

A

1001-0505(2017)06-1129-06

2017-05-28.

刘勇(1990—),男,硕士生;王开(联系人),男,博士,副教授,wangkai-seu@163.com.

国家自然科学基金资助项目(61401094,61771124)、江苏省自然科学基金资助项目(BK20140645)、中央高校基本科研业务费专项资金资助项目(2242016K41050).

刘勇，王开，刘航，等.基于总体最小二乘改进的SDFT三相交流电频率估计算法[J].东南大学学报(自然科学版),2017,47(6):1129-1134.

10.3969/j.issn.1001-0505.2017.06.008.