过山脊内孤立波演变及其对细长潜体的作用力特性1)

谷梦梦 魏 岗 邓 冰 杜 辉 武军林

*(国防科技大学气象海洋学院，南京211101)

†(94758部队气象台，福建宁德352000)

**(北京应用气象研究所，北京100029)

过山脊内孤立波演变及其对细长潜体的作用力特性1)

谷梦梦*,†魏 岗*,2)邓 冰**杜 辉*武军林*

*(国防科技大学气象海洋学院，南京211101)

†(94758部队气象台，福建宁德352000)

**(北京应用气象研究所，北京100029)

内孤立波沿山脊地形传播过程中的结构变化使得影响海洋结构物及水下航行器安全的不确定因素增加，用大型重力式分层流试验水槽系统研究内孤立波过山脊地形及其对细长潜体作用力特性，可有效提高对其危害性机理的认识.为此，利用电导率探头阵列,结合染色标识方法,测量内孤立波演变特性，同时利用三分量传感器测量水下细长体模型受力特性.研究结果表明：山脊地形显著改变下凹型内孤立波结构，表现为坡前波幅增大，坡顶背风波面抬升，坡后波长变长；内波结构变化直接影响细长体受力特性，表现为坡前向下作用力明显增强，坡顶向上作用力突显，坡后作用力持续时间变长；细长体受力特性变化影响其运动趋势，坡前下沉运动增强、朝山脊方向纵荡运动显著.

内孤立波，分层流，山脊地形，细长潜体，作用力测量

引言

大陆架边缘向深海区域延伸的海洋底部地形复杂，海脊是其典型结构之一，也是显著影响海洋内波生成与传播的重要环境因素[1-2].例如，在台湾南端至菲律宾以西的吕宋海槽外侧，分布着长达数百海里的海底山脊，南中国海北部的内孤立波多在这一区域激发形成[3-4]，受其影响,内孤立波在传播过程中的波形、波幅和波速等特征会发生非定态变化，可引起大振幅波破碎以及跃层附近密度场的强烈混合，极大地增加了影响海洋结构物和水下航行体安全的不确定因素[5-7].

海洋底部边界常呈复杂的非规则结构.从几何上简化地形结构是认识海洋内孤立波与复杂海底地形作用的基本做法，可以揭示此类问题的一系列重要特征[8-12].台阶是一类简单突变地形结构.魏岗等[13]基于边缘层理论探讨了两层流体中内孤立波在台阶地形上的演变特征，揭示了流层厚度比、密度比和台阶高度等参数的影响规律；屈子云等[14]通过水槽实验研究内孤立波沿台阶地形的演变特征，获得了内孤立波极性转换的基本规律；Lee[15]基于黏性数值计算模型，揭示了阻塞和非线性效应是影响内孤立波与地形相互作用的关键因素.斜坡作为陆坡架结构的一种近似地形，杜辉等[16]通过水槽实验研究了不同坡度地形下内孤立破碎条件，揭示了能量损失出现跃升是发生破碎的重要特征；Michallet等[17]采用PIV实验技术对不同地形坡度、分层厚度比和密度比条件下内孤立波破碎的精细测量，建立了波长和斜坡特征长度与内孤立波斜坡反射能之间的关系.三角形地形常作为海底山脊的一种简单近似，Chen等[18]实验研究了内孤立波经过底部三角形地形的特征结构，详细描述了下凹形内孤立波产生的强烈水跃及持续的伴随涡流扩散特征；Xie等[19]通过构建潮汐与山脊相互作用数值模型，证实了正压潮流经不同坡度山脊时内孤立波通常在坡度较大一侧被激发的事实；Zhu等[20]数值模拟了两层流体中大振幅内孤立波和山脊的相互作用，提出了基于非线性波动效应和地形特征变化的修正阻塞参数；高国兴等[21]的数值计算表明潮流与地形相互作用形成下陷结构是内孤立波生成的重要原因.

有关内孤立波与海洋平台、水下圆柱等结构物的相互作用，国内外学者在数值和实验上均已有大量研究成果[22-25]，对于内孤立波中结构物受力特性认识有着重要的参考价值.另一方面，内孤立波可以改变对水下细长潜体的作用力特性，其影响不容忽视.例如，关晖等[26]基于湍流k--ε的数值计算进一步证实了细长潜体穿越内孤立波时受到的垂向和水平向作用力会在较短时间内发生突变；付东明等[27]通过构建数值内波水槽模拟了细长潜体遭遇内孤立波的过程，获得了内孤立波作用下潜体附加载荷变化规律；Wei等[28]在大型分层流水槽中测量了细长潜体受到的内孤立波作用力，所获结果验证了最大内孤立波载荷特性；Du等[29]尝试开展了缓坡地形对内孤立波及其细长潜体作用力特性影响的实验研究，获得了内孤立波结构变化对作用力特性影响的初步结果.显而易见，海底地形引起内孤立波结构的时空变化将使得作用于潜体的力学特性更为复杂，对于山脊等复杂地形效应影响细长潜体内孤立波作用力特性的认识目前尚不清楚.

为此，本文将海底山脊简化为分层流试验水槽底部的三角形地形结构，采用电导率阵列测波技术和三分量传感器测力技术，同时结合染色显示方法，开展内孤立波沿山脊地形传播及其对细长潜体作用力的实验研究，以期深入地了解内孤立波沿山脊地形的演变规律，定量地获得其在传播过程中对细长潜体作用力的变化规律.

1 实验设置与方法

实验在大型重力式分层流试验水槽中进行[28]，图1为实验原理示意图.试验水槽主尺度为12m×1.2m×1.0m(长×宽×高)，两端分别安装有重力式内孤立波造波机和三角楔形消波装置，可在任意跃层位置产生下凹型或上凸型内孤立波，以及通过调节最佳楔角有效消除反射波的影响；采用“双缸法”制取分层流体环境，以形成总深度H=0.8m、上下层流体厚度h1=0.2m和h2=0.6m、密度为ρ1=999kg/m3和ρ2=1017.5kg/m3的两层流体系统；细长潜体模型采用有机玻璃材料，其长度和直径分别为0.75m和0.09m；三角地形由两块长L=2.0m和宽D=1.2m的薄平板(材质为聚氯乙烯，密度略大于盐水)拼接组成，其高hs=0.5m.图中其他符号包括：a0,λ0和c0分别为初始内孤立波波幅、波长和传播速度，η0和L0分别为内孤立波造波原理中的初始方势阱深度和宽度[30].

建立水槽系统中直角坐标系xOz，其坐标原点O位于山脊坡顶处的静止水面，正x轴沿水槽长度方向从左至右，正z轴沿铅垂方向由下至上.采用电导率探头阵列技术测量沿地形演变的内孤立波结构，选取水平位置 I(x=2.69m)，II(x=2.0m)，III(x=1.5m)，IV(x=1.0m)，V(x=0.5m)，VI(x=0.0m)，VII(x= −0.5m)，VIII(x= −1.0m)布置电导率探头阵列，其中位置I,II,IV,V,VI,VII,VIII处分别垂向设置间距为0.03m的7只探头，位置III设置1只探头；位置I处探头阵列可用来测量无地形内孤立波结构，位置II,IV,V,VI,VII,VIII处探头阵列用以测量演化内孤立波的波形、波幅和波速.同时，借助染色界面标识和高分辨摄录系统记录内孤立波结构的连续变化.

将细长潜体模型分别设置于无地形位置I和地形位置V,VI,VII处，通过调整垂向坐标来控制模型潜深位置.利用三分量测力传感器测量模型受到的内孤立波作用力，包括x轴水平力、z轴垂向力和xOz平面扭矩.

实验中有关物理量参数的无量纲化形式如下

式中，Fx,Fy分别为实测的水平力和垂向力(N)，β为水平迎水面积(m2)，ρ为模型所在深度的流体密度(kg/m3)，g为重力加速度(m/s2).

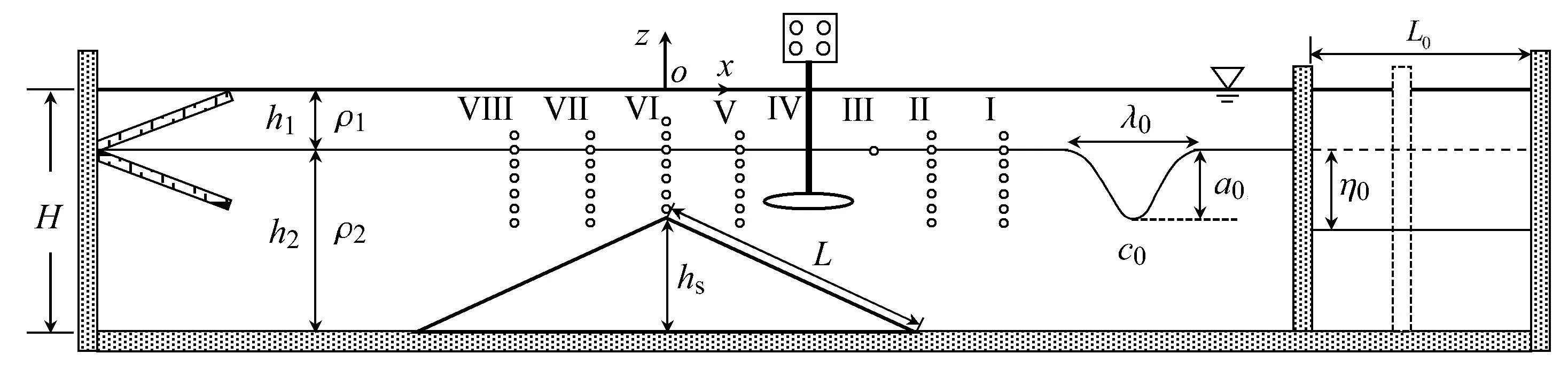
图1 实验原理示意图Fig.1 Schematic diagram for experimental principle

2 试验结果与分析

2.1 山脊地形内孤立波传播特性

2.1.1 波形

图2记录了下凹型内孤立波沿山脊地形传播的可视化典型特征，以及对应探头阵列在跃层z/H=−20/80处位置II,IV,V,VI,VII,VIII记录的密度时间序列变化值.位置II记录了入射地形前的单峰内孤立波波形，位置IV和V记录了在山脊坡前不同位置的波形.在爬坡过程中,波形在水平向逐渐变宽再收窄,在铅垂向明显拉伸,波幅逐渐增大，约在坡前x/L=1/4位置达到最大，可见内孤立波在向山脊顶部传播过程中振幅更大.位置VI记录了内孤立波在山脊顶部的波形，其迎风波面受坡顶高度阻挡、背风波面被挤压抬升，导致垂向伸展急剧减小，同时背风波面迅速发展出“上涌”型的尾部结构，此位置产生的破碎可引起跃层内不同密度流体的强烈混合；位置VII和VIII记录了在山脊坡后波形的变化，其水平向变得更宽、垂向伸展范围急剧缩小.

2.1.2 波幅

图3为内孤立波沿山脊地形传播过程中不同水平位置处波幅变化特性，其中横坐标代表内孤立波传播距离，纵坐标为无量纲波幅值.由图可知，在山脊坡前位置，波幅呈逐渐增大趋势，初始波幅愈大受地形影响愈明显，图中最大增幅达到30%；在山脊顶部附近，波幅急剧减小，图中最大减幅达50%；之后，在山脊坡后位置，波幅变化率逐渐趋于平缓.

图2 内孤立波沿山脊地形传播可视化图及其等密度时间序列值Fig.2 Visualization diagram and density isolines of a propagating ISW over a ridge terrain

图3 内孤立波波幅沿山脊地形变化Fig.3 Varying amplitudes of the ISW over a ridge terrain

2.1.3 波速

利用沿跃层水槽长度方向间距为∆x的两只电导率探头，记录内孤立波经过时两探头电导率扰动峰值间的时间间隔∆t，可获得内孤立波传播速度c=∆x/∆t，图4纵坐标为内孤立波沿山脊地形传播波速变化无量纲值.由图可知，下凹型内孤立波波速从位置II至山脊坡前位置V逐渐减小，在山脊顶部附近迅速衰减并达最小值，且波幅愈大衰减愈剧烈，图中最大波幅的降速可达54%；重力作用使得山脊坡后内孤立波下坡速度明显增大，波幅愈大波速增幅愈大，图中位置VIII(x/L=−1/2)处对应最大波幅之波速为坡顶VI(x/L=0)的6.6倍.

图4 内孤立波波速沿山脊地形变化Fig.4 Varying velocities of ISW over a ridge terrain

2.2 山脊地形内孤立波与细长潜体相互作用特性

内孤立波传播过程中造成密度跃层流动的剪切状态，可对潜体产生剪切作用[26]，影响其运动状态和受力特性，在起伏不平的海底地形作用下，流动剪切结构的变化将显著改变对潜体的作用力特性及其运动趋势.本节着重分析内孤立波入射波幅、潜体潜深和潜体水平位置等变化对潜体作用力特性的影响.

2.2.1 入射波幅对作用力特性影响

将细长潜体设置于无地形位置I及山脊地形三处典型位置，即坡前V、坡顶VI和坡后VII，保持模型位于跃层z/H=−20/80处，改变入射内孤立波波幅，可获得不同波幅作用下模型的受力特性.

内孤立波波形结构变化直接影响模型的受力特性，试验首先比较了上述位置不同入射波幅之波形结构，如图5所示.

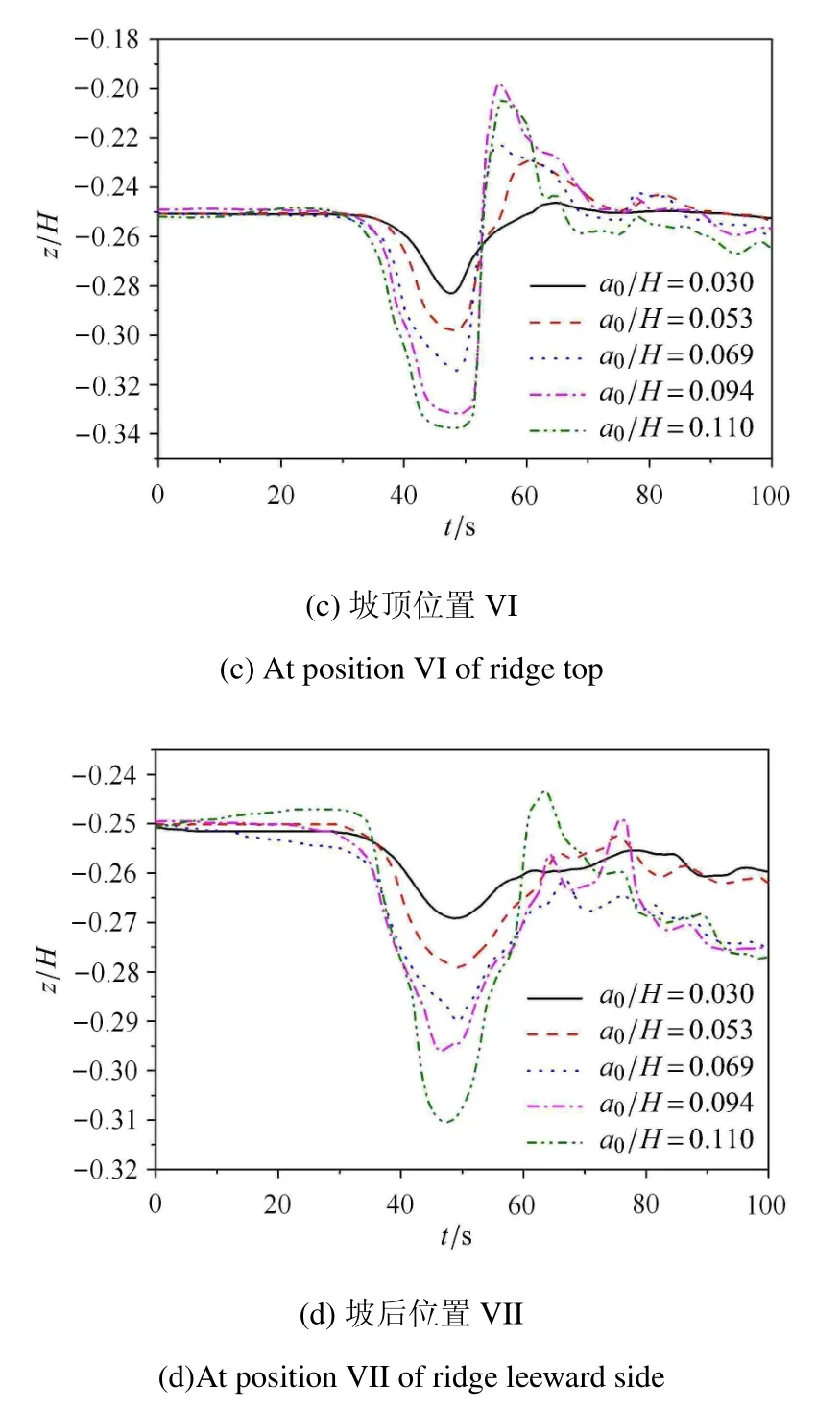
图5 不同入射波幅内孤立波的波形结构Fig.5 Structure of ISW for di ff erent wave amplitudes

图中对于小振幅入射波，如a0/H为0.03,0.053的波形受地形影响较小，波幅变化不大；对于较大振幅入射波，如a0/H=0.069,0.094,0.11时，波形在坡前受地形影响,波幅明显增大，入射波幅越大,变化越明显，波形后部无明显尾波列出现；在坡顶，相对坡前波幅明显减小,水平影响范围变宽，阻塞效应导致波形背风面抬升、尾部出现破碎和波列.随着波幅增加、背风面抬升和破碎显著增强，尾波列形成，图中向上最大抬升为向下波幅值的60%；在坡后，波幅随入射波幅成正比增加,相对在坡顶波幅有所减小，水平影响范围更宽，背风面抬升消失，尾部波列延续.

图6∼图9分别为潜体在无地形位置I及山脊坡前V、坡顶VI和坡后VII处对于不同波幅入射波的受力特性曲线.

由图6可知，对于无地形情形，入射波幅增大使得潜体所受水平力和垂向力均增大，波幅a0/H从0.03增至0.11,水平力增至3倍，垂向力增至2.1倍.水平力先沿x轴正向、再转为沿x轴负向，前者增幅大于后者；垂向力方向沿z轴负向，表现为向下拽力，其大小随入射波幅增大而增大、远高于水平力(近1个量阶).此时，细长潜体运动趋势为：水平方向先向前再向后、前者运动幅度大于后者，铅垂方向明显下沉,入射波幅增大使这种趋势增强.

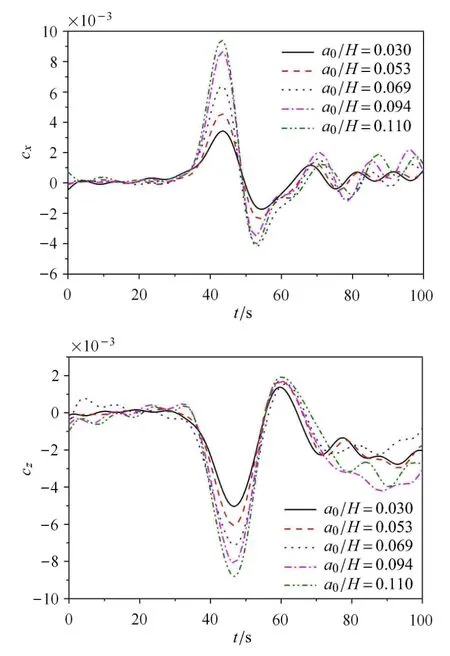
图6 无地形时波幅变化对潜体作用力时程曲线Fig.6 ISW forces vs.time for di ff erent wave amplitudes without terrain

由图7可知，与无地形位置I比较，在山脊坡前，入射波幅变化不影响模型受力方向的变化，仅改变其大小，波幅a0/H从0.03增至0.11,水平力最大增至2.8倍，垂向力最大增至1.6倍；水平负向力增强、正向力减弱，随入射波幅增大前者增幅大于后者；垂直向下拽力增加，波幅愈小增幅愈大，图中最小波幅的垂向力增加40%、最大波幅的垂向力增加13%.此时，模型运动趋势变化为：向后运动幅度小于向前的，其水平向着山脊运动、垂直向下运动趋势变得更为显著.

图7 山脊坡前波幅变化对潜体作用力时程曲线Fig.7 ISW forces vs.time for di ff erent wave amplitudes on the windward side of ridge

由图8可知，与无地形情形比较，在坡顶位置，水平力及垂向力随入射波幅增加而增大，波幅达到一定值后它们增幅均减小，波幅a0/H从0.03增至0.11水平力最大增至2.4倍，垂向力最大增至1.8倍.水平力沿x轴正向大幅减小,往复作用增强,随时间变化逐渐减弱；垂向力方向和幅值变化较小,作用周期变长.尽管相同入射波波幅在坡顶变小，但向下拽力并未明显减小，内孤立波造成的密度跃层混合部分抵消了上浮力.此时，模型运动趋势表现为：水平往复运动加强,向前运动幅度大于向后幅度，铅垂向仍保持显著的下沉运动,并伴随弱的垂荡.

图8 山脊坡顶波幅变化对潜体作用力时程曲线Fig.8 ISW forces vs.time for di ff erent wave amplitudes at the top of ridge

由图9可知，与无地形情形比较，在坡后位置，波幅a0/H从0.03增至0.11,水平力增至1.7倍，垂向力增至1.7倍.水平力从x轴正方向转为x轴负方向，且前者衰减明显大于后者，图中二者最大减幅分别达81%和29%，并伴有强烈的往复作用；垂向向下拽力略有减小，向上推举力增大，图中增幅可达1倍以上.此时，潜体运动趋势表现为：水平向前运动幅度变为小于向后运动，潜体背离山脊运动趋势明显，铅垂向先保持较强下沉运动，之后上浮运动趋势明显.

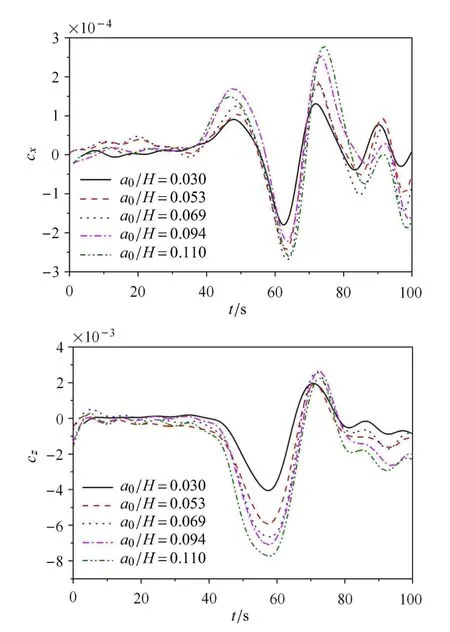
图9 山脊坡后波幅对潜体作用力的时程曲线Fig.9 ISW forces vs.time for di ff erent wave amplitudes on the leeward side of ridge

2.2.2 模型潜深位置对作用力特性影响

将细长潜体同样设置于无地形位置I及山脊地形三处典型位置(坡前V、坡顶VI和坡后VII)，保持入射下凹型内孤立波波幅a0/H=0.069不变，改变潜体的深度位置，可获得不同潜深位置的受力特性.由于不同深度内孤立波结构受地形影响的差异，继而改变受力特性，为此，实验首先比较了上述位置不同深度处的内孤立波结构，如图10所示.

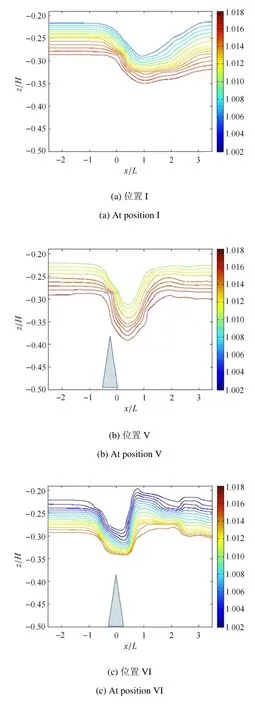
图10 内孤立波在位置I、V、VI和VII处不同深度等密度时程曲线Fig.10 Density isolines for di ff erent depths of ISW at positions I,V,VI and VII

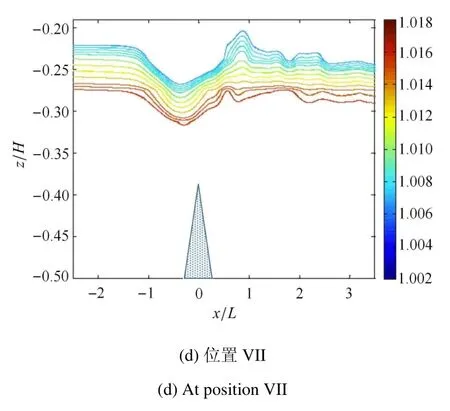
图10 内孤立波在位置I、V、VI和VII处不同深度等密度时程曲线(续)Fig.10 Density isolines for di ff erent depths of ISW at positions I,V,VI and VII(continued)

在无地形位置I，内孤立波等值线密度值至上而下依次增加，其位移值在跃层位置z/H=−20/80处达到最大，可用来表示波形、波幅等结构特征，该位置至下而上及至上而下的位移依次减小，前者较后者衰减得更快；在坡前位置V，受地形影响波形在不同深度沿铅垂方向均有拉伸变形、导致波幅增大，且深度增加拉伸愈明显；在坡顶位置VI，从跃层下方变化至跃层上方，波背风面“抬升”逐渐变强、破碎并伴有尾波列产生，跃层下方波形受地形阻挡明显使得波腹变窄，而跃层上方波形因距离坡顶较远使得波腹变宽，跃层上方波幅平均小于跃层下方；在坡后位置VII，不同深度波形均受到地形影响，波幅均显著减小、尾波列形成.

图11∼图14分别为模型在无地形和山脊典型位置不同深度处受力的时程曲线.

图11对应无地形情形，图中z/H=−10/80,−15/80位于跃层上方，z/H=−20/80为跃层位置，z/H= −25/80,−30/80,−40/80均位于跃层下方，且z/H=−25/80恰为模型穿越内孤立波的潜深位置.随深度增加水平力最大增幅达6.9%，垂向力从z/H=−10/80至跃层z/H=−20/80增至26倍.水平力从跃层位置至其上方逐渐增加，表现为先x轴正方向,后转为x轴负方向,再往复作用；跃层位置处正向力大于负向力；在跃层下方水平力随深度增加而增大，其方向为先x轴负方向,再转向x轴正方向,之后往复作用，在穿越内孤立波位置作用最小且沿x轴正方向.垂向力保持向下，在跃层上方随深度增加而逐渐增大；在跃层处z/H=−20/80达到最大值；在跃层下方随深度增加，在穿越内孤立波位置达到最大，之后迅速减小直至达到零值.此时，细长潜体运动趋势为：当潜深位置至上而下变化时，水平运动在跃层及上方表现为先向前再向后，往复运动幅度逐渐减小，在跃层下方运动方向和幅度变化则相反；铅垂方向为明显下沉运动，其在跃层处最大,穿越位置次之,之后随深度增加迅速减小.

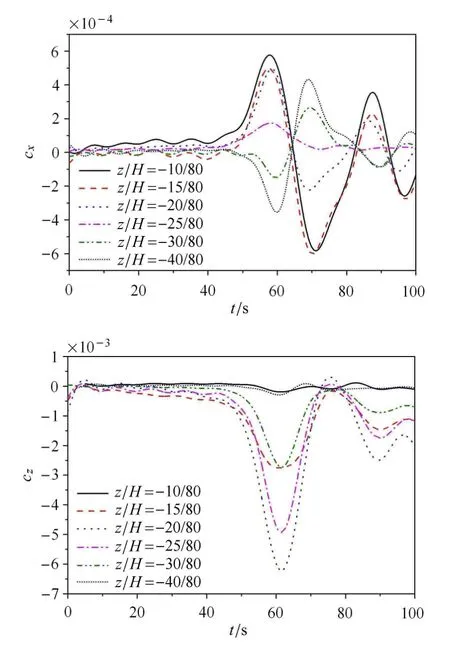
图11 模型在无地形位置不同潜深处受力时历曲线Fig.11 ISW forces vs.time for di ff erent depths without terrain

图12对应山脊坡前位置，随深度增加水平力最大增幅达24%，z/H从−10/80增至−20/80,垂向力增至27倍.与无地形情形比较，因内孤立波波幅在坡前增大使其对潜体的作用明显增强.水平力方向变化基本保持不变，但跃层及其上方x轴负向力增加,x轴正向力减小，前者为后者的2.1倍；跃层处正、负方向力相当；跃层下方x轴负向力减小,x轴正向力增加，后者为前者的1.8倍，穿越内孤立波位置的水平力最小但方向逆反.垂向力在跃层及其上方作用较小，出现沿z轴负再变为z轴正的往复作用，即先向下再向上，z/H=−15/80处上下作用力相当，z/H=−20/80处向下作用远大于向上作用，图中前者约为后者的3倍；垂向力在跃层下方主要沿z轴负方向，在穿越内孤立波位置达到最大，之后随深度增加迅速减小.图中z/H=−25/80较无地形情形增加70%.此时，潜体运动趋势为：水平往复运动规律不变，其在跃层及上方x轴负方向的运动明显大于x轴正方向，即朝着山脊方向运动增强；模型垂向运动在跃层及上方出现往复变化，在跃层下方尤其是穿越内孤立波位置，向下运动显著增强，故应特别关注该位置的下沉位移.

图12 模型在山脊坡前不同潜深处受力时程曲线Fig.12 ISW forces vs.time for di ff erent depths on the windward side of ridge

图13对应山脊坡顶位置，随深度增加水平力最大增幅达0.8%，z/H从−10/80增至−20/80,垂向力增至8倍.与无地形情形比较，水平力方向变化不受影响，但在跃层及其上方x轴正向力变为x轴负向力，前者减小、后者明显增大，图中最大增幅接近40%；在穿越内孤立波位置水平力方向发生逆转，正、负向作用力显著增加，图中增幅达3∼4倍.垂向力在跃层及其上方出现先向下再向上的往复作用，且在跃层位置垂向力达到最大，在z/H=−20/80处负向力是正向力的6.8倍，最大增幅为无地形情形的34%；在穿越内孤立波位置之后垂向力随深度增加逐渐减小，在z/H=−20/80处的增幅为50%.此时，潜体运动趋势为：至上而下水平往复运动规律不变，但跃层及上方x轴负方向运动明显大于x轴正向，在穿越内孤立波位置,x轴正负方向运动均显著增强,使得纵荡运动增强；铅垂方向在跃层上方先向下再向上运动，在跃层及下方下沉运动显著，最大下沉位置在跃层处.

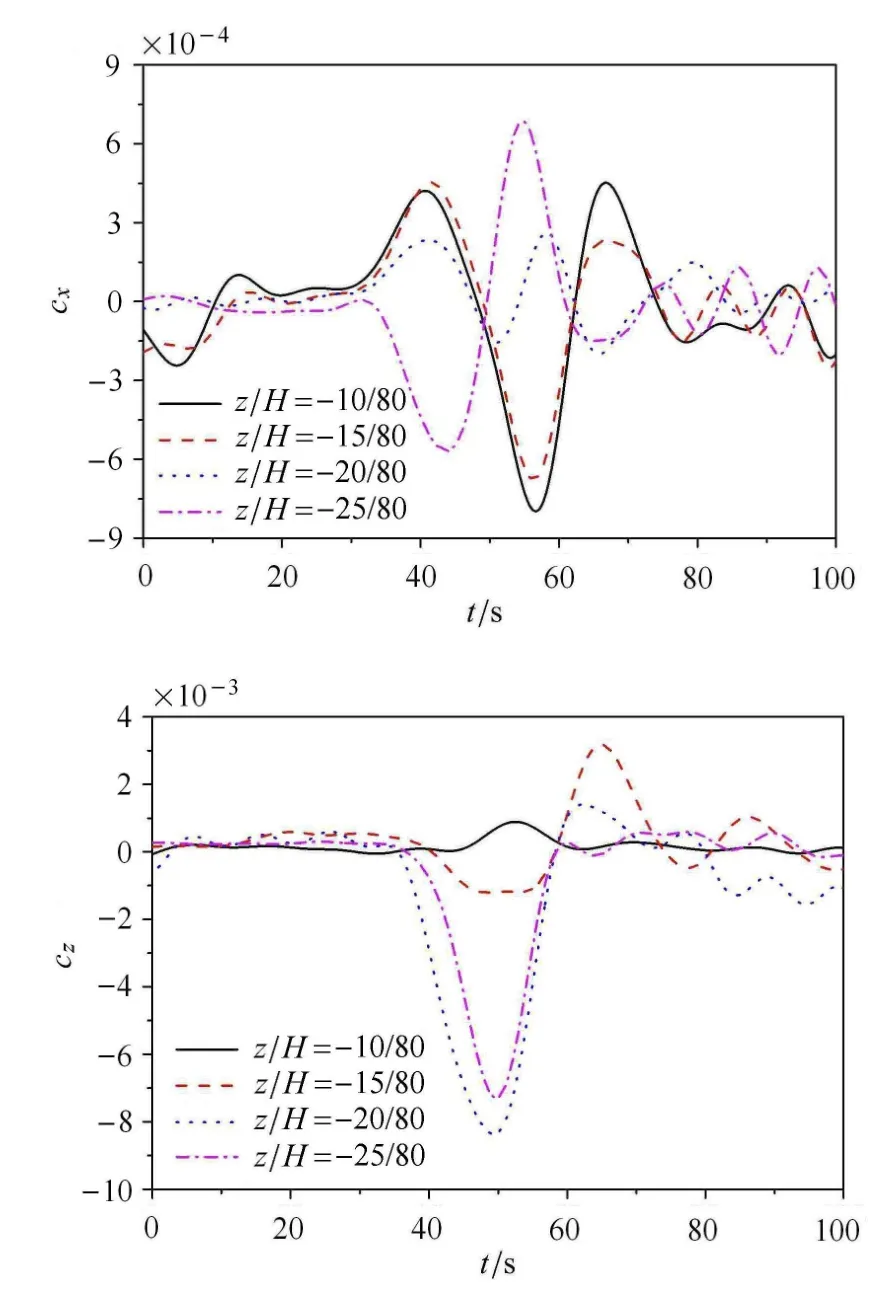
图13 模型在山脊坡顶位置不同潜深处受力时程曲线Fig.13 ISW forces vs.time for di ff erent depths at the top of ridge

图14对应山脊坡后情形，随深度增加,水平力在z/H=−10/80最大处，z/H从−10/80增至−20/80,垂向力增至24倍.水平力变化类似于山脊顶部，但在跃层及其上方,x轴正向力变为x轴负向力，前者减小,后者增加，图中两者最大变化幅度分别为35%和38%；在穿越内孤立波位置时，水平力明显增强.垂向力变化也类似于山脊顶部，但各潜深位置作用强度明显降低，在z/H=−25/80处,衰减幅度为26%.此时，潜体运动趋势为：模型运动方向变化规律不变，但跃层及上方x轴负方向运动明显大于x轴正向，两者变强使得纵荡运动明显增加，尤其背离山脊运动的趋势增强，在z轴负方向主要表现为下沉运动,并伴有尾部抬升运动，下沉运动在跃层位置达到最大,在穿越内孤立波位置次之,在跃层下方迅速减小.

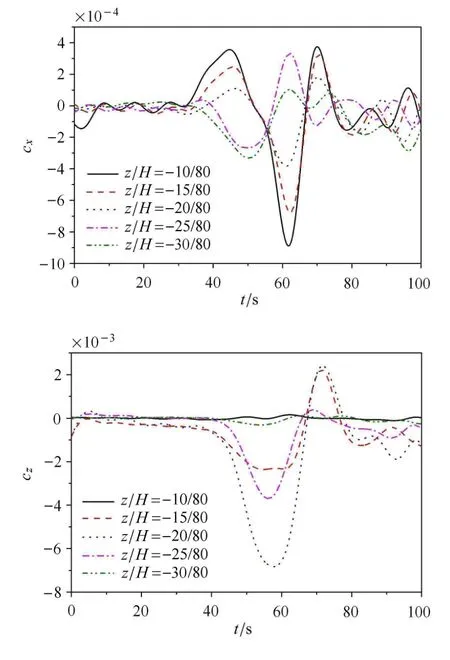
图14 模型在山脊坡后位置不同潜深处的受力时程曲线Fig.14 ISW forces vs.time for di ff erent depths on the leeward side of ridge

2.2.3 水平位置模型作用力特性比较

以入射波幅a0/H=0.069和潜深位置z/H=−20/80为例，图15进一步比较了位置I,V,VI和VII的波形及对应模型的受力特性.图15(a)中，与无地形位置I处比较，下凹型内孤立波在坡前V波幅最大，在坡顶VI波幅迅速减小、波形后部抬升、尾部产生波列并伴随破碎，在坡后VII波幅进一步减小、波长变长.由图15(b)可知，用纵坐标R表示作用力极差值(最大与最小值之差绝对值)，则水平极差值在无地形位置I处最大、坡顶VI最小，垂向极差值在坡前V最大、坡后VII最小.据此，可判断模型沿山脊传播过程中的运动变化趋势为：水平纵荡经历了减小再缓慢增加过程，最小纵荡在坡顶达到；垂向下沉经历了逐渐增加再减小过程，最大下沉在坡前达到.

图15 沿山脊不同水平位置波形及其对细长潜体作用力极差分布图Fig.15 Waveforms of ISW and range charts of its action on a submerged body along di ff erent horizontal position over a ridge

3 结论

在大型重力式分层流水槽中采用内波动态测量及内波微幅力测量技术研究了下凹型内孤立波沿山脊地形传播及其对细长潜体作用力特性，获得的主要结论如下：

(1)山脊地形显著改变下凹型内孤立波特征结构，其波形在坡前垂向拉伸变窄、在坡顶背风波面形成的“上涌”导致破碎和混合、坡后垂向收缩变宽；波幅在坡前逐渐变大并随入射波振幅增大而增大、坡顶急剧减小、坡后变化平缓；波速在坡前和坡后分别经历急剧减速和加速过程、坡顶最小.

(2)下凹型内孤立波结构变化影响对细长潜体作用力特性：入射波幅增大作用力增强，水平往复作用在坡前朝山脊方向强、在坡后背离山脊方向强，铅垂向下作用在坡前最大、在跃层及其上方出现往复作用；潜深位置改变作用力方向，在跃层及上方水平力先正后负、垂向力先向下再向上，在跃层下方水平力先负后正、垂向力始终保持向下.

(3)内孤立波作用力特性决定细长潜体运动特征：纵荡在坡前向着山脊方向趋势强、在坡后背离山脊方向趋势强；垂向在跃层及上方为先下沉再上浮运动趋势，在跃层下方为下沉趋势，且坡前下沉最显著.

1 方欣华，杜涛.海洋内波基础和中国海内波.青岛：中国海洋大学出版社，2005.(Fang Xinhua,Du Tao.Fundamentals of Oceanic Internal Waves and Internal Waves in the China Seas.Qingdao:Ocean University of China Press,2005(in Chinese))

2 冯文科，鲍才旺.南海地形地貌特征.海洋地质研究，1982，2(4)：80-93(Feng Wenke,Bao Caiwang.Topographic and geomorphological characteristics of South China Sea.Marine Geological Research,1982,2(4):80-93(in Chinese))

3 Yang YJ,Tang TY,Chang MH,et al.Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies.IEEE Journal of Oceanic Engineering,2004,29(4):1182-1199

4 Wang J,Sun ML,Zhang XD,et al.A numerical study of the generation mechanism of internal solitary waves in the Luzon Strait.Acta Oceanologica Sinica,2015,34(7):38-43

5 蔡树群，何建玲，谢皆烁.近10年来南海内孤立波的研究进展.地球科学进展，2011，26(7):703-710(CaiShuqun,HeJianling,Xie Jieshuo.Recent decadal progress of the study on internal solitons in the south china sea.Advances in Earth Science,2011,26(7):703-710(in Chinese))

6 黄文昊，林忠义，尤云祥.内孤立波作用下Spar平台动力响应特性.海洋工程，2015，33(2)：21-31(Huang Wenhao,Lin Zhongyi,You Yunxiang.Dynamic response characteristics of a spar platform under internal solitary waves.Ocean Engineering,2015,33(2):21-31(in Chinese))

7 Wang Y,Wang LL,Zhu H,et al.A numerical study of the forces on two tandem cylinders exerted by internal solitary waves.Mathematical Problems in Engineering,2016,1:1-15

8 Hsieh CM,Cheng MH,Hwang RR,et al.Numerical study on evolution of an internal solitary wave across anidealized shelf with different front slopes.Applied Ocean Research,2016,59:236-253

9 黄鹏起，陈旭，孟静等.内孤立波破碎所致混合的实验研究.海洋与湖沼，2016，47(3)：533-539(Huang Pengqi,Chen Xu,Meng Jing,et al.An experimental study on mixing induced by internal solitary wave breaking.Oceanologia Et Limnologia Sinica,2016,47(3):533-539(in Chinese))

10 Li Q,Xu ZH,Yin BS,et al.Modeling the interaction of an internal solitary wave with a sill.Acta Oceanologica Sinica,2015,34(11):32-37

11 Hsieh CM,Hwangb RR,Hsu JRC,et al.Numerical modeling of flow evolution for an internal solitary wave propagating over a submerged ridge.Wave Motion,2015,55:48-72

12 尤云祥，徐杰，魏岗等.连续分层流体中垂直薄板的水动力特性.力学学报，2007，39(3):297-310(You Yunxiang,Xu Jie,Wei Gang,et al.Hydrodynamic characteristics of vertical thin barrier in a continuously strati fi ed fl uid.Chinese Journal of Theoretical and Applied Mechanics,2007,39(3):297-310(in Chinese))

13 魏岗，尤云祥，缪国平等.分层流体中内孤立波在台阶上的反射和透射.力学学报，2007，39(1):45-53(Wei Gang,You Yunxiang,Miao Guoping,et al.Re fl ection and transmission of an internal solitary wave over a step in strati fi ed fl uid.Chinese Journal of Theoretical and Applied Mechanics,2007,39(1):45-53(in Chinese))

14 屈子云，魏岗，杜辉等.下凹型内孤立波沿台阶地形演化特征试验.河海大学学报(自然科学版)，2015，43(1)：85-89(Qu Ziyun,Wei Gang,Du Hui,et al.Experimental on the evolution characteristics of internal solitary wave of depression over step topography.Journal of Hohai University(Natural Sciences),2015,43(1):85-89(in Chinese))

15 Lee MP.Numerical simulation of nonlinear internal solitary wave interactions with submarine topographic features.[PhD Thesis].Washington:The Catholic University of America,2011

16 杜辉，魏岗，曾文华等.缓坡地形上内孤立波的破碎及能量分析.海洋科学，2014，38(10)：98-104(Du Hui,Wei Gang,Zeng Wenhua,et al.Breaking and energy analysis of internal solitary wave over a gentle slope.Marine Sciences,2014,38(10):98-104(in Chinese))

17 Michallet H.,Ivey GN.Experiments on mixing due to internal solitary waves breaking on uniform slopes.Journal of Geophysical Research,1999,104(C6):13467-13477

18 Chen CY.An experimental study of strati fi ed mixing caused by internal solitary waves in a two-layered fl uid system over variable seabed topography.Ocean Engineering.2007,34:1995-2008

19 Xie JS,Cai SQ,He YH.A continuously strati fi ed nonlinear model for internal solitary waves in the northern South China Sea.Chinese Journal of Oceanology and Limnology,2010,28(5):1040-1048

20 Zhu H,Wang LL,Avital EJ,et al.Numerical simulation of interaction between internal solitary waves and submerged ridges.Applied Ocean Research,2016,58:118-134

21 高国兴，刘翠华，祝传刚等.单一海脊地形对海洋内波生成与传播影响的分析.热带海洋学报，2015，34(3)：23-29(Gao Guoxing,Liu Cuihua,Zhu Chuangang,et al.Analysis of single-ridge topography impact on internal waves’generation and propagation.Journal of Tropical Oceanography,2015,34(3):23-29(in Chinese))

22 黄文昊，尤云祥，王旭等.圆柱型结构内孤立波载荷实验及其理论模型.力学学报，2013，45(5):1-13(Huang Wenhao,You Yunxiang,Wang Xu,et al.Internal solitary wave loads experiments and its theoretical model for a cylindrical structure.Chinese Journal of Theoretical and Applied Mechanics,2013,45(5):1-13(in Chinese))

23 SongZJ,TengB,GouY,etal.Comparisonsofinternalsolitarywave and surface wave actions on marine structures and their responses.Applied Ocean Research,2011,33(2):120-129

24 Si ZS,Zhang YL,Fan ZS.A numerical simulation of shear forces and torques exerted by large-amplitude internal solitary waves on a rigid pile in South China Sea.Applied Ocean Research,2012,37(37):127-132

25 张新曙，胡晓峰，尤云祥等.深海多立柱浮式平台涡激运动特性研究.力学学报，2016，48(3)：593-598(Zhang Xinshu,Hu Xi-aofeng,You Yunxiang,et al.Investigation on the characterisitics of vortex induced motion of a deep sea muti-column fl oating platform.ChineseJournalofTheoreticalandAppliedMechanics,2016,48(3):593-598(in Chinese))

26 关晖，魏岗，杜辉.内孤立波与潜艇相互作用的水动力学特性.解放军理工大学学报(自然科学版)，2012，13(5)：577-582(Guan Hui,Wei Gang,Du Hui.Hydrodynamic properties of interactions of three-dimensional internal solitary waves with submarine.Journal of PLA University of Science and Technology(Natural Science Edition),2012,13(5):577-582(in Chinese))

27 付东明，尤云祥，李巍.两层流体中内孤立波与潜体相互作用数值模拟.海洋工程，2009，27(3)：38-44(Fu Dongming,You Yunxiang,Li Wei.Numerical simulation of internal solitary waveswith a submerged body in a two-layer fl uid.Ocean Engineering,2009,27(3):38-44(in Chinese))

28 Wei G,Du H,Xu XH,et al.Experimental investigation of the generation of large-amplitude internal solitary wave and its interaction with a submerged slender body.Science China:Physics,Mechanics&Astronomy,2014,57(2):301-310

29 Du H,Wei G,Gu MM,et al.Experimental investigation of the load exerted by nonstationary internal solitary waves on a submerged slender body over a slope.Applied Ocean Research,2016,59:216-223

30 Whitham GB.Linear and Nonlinear Waves.Hobo Ken:John Wiley and Sons.Inc.1974

EXPERIMENTAL INVESTIGATION ON THE EVOLUTION OF INTERNAL SOLITARY WAVE OVER A RIDGE AND ITS ACTING FORCES ON A SUBMERGED SLENDER BODY1)

Gu Mengmeng*,†Wei Gang*,2)Deng Bing**Du Hui*Wu Junlin*
*(College of Meteorology and Oceanography，National University of Defense Technology，Nanjing211101，China)
†(Meteorological Observatory of94758Troops，Ningde352000，Fujian，China)
**(Beijing Applied Meteorology Institute，Beijing100029，China)

The con fi guration of internal solitary wave(ISW)over a ridge terrain will largely increase the uncertain factors threatening the safety for marine architecture and submerged vehicle.Laboratory experiments are conducted to examine an ISW propagating over a ridge terrain and its interaction with a submerged slender body in a large-type gravity strati fi ed fluid tank.The evolution characteristics of the ISW is measured by using multi-channel conductivity-probe arrays and dyeing identi fi cation method,and its action on the body exerted by the ISW is measured by a set of three-component force sensor.The experimental results have shown that when an ISW of depress propagates over a ridge terrain its wave con fi guration will be changed signi fi cantly,including that its amplitude will increase on the windward side of ridge,its lee side will be up at the top of ridge and its wavelength will be longer on the leeward side of ridge.Furthermore the con fi guration change of the ISW will a ff ect obviously the characteristics of the action on a slender body,including that the downward force becomes larger distinctly on the windward side of ridge,the upward force is more signi fi cant at the top of ridge and the e ff ective time of the action on the body becomes longer at the leeward side of ridge.Therefore,the body movement trend can be judged roughly based on the force behaviors,i.e.the largest sinking will happen on the windward side of ridge and the stronger surging towards the direction of ridge will do on the windward side of ridge.

internal solitary wave，strati fi ed fl uid，ridge，slender body，force measurement

O352

A doi：10.6052/0459-1879-16-322

2016–11–08 收稿，2017–09–01 录用,2017–09–03 网络版发表.

1)国家自然科学基金资助项目(11072267,11472307).

2)魏岗，教授，主要研究方向：水动力学，实验流体力学.E-mail:weigangweigang12@163.com

谷梦梦,魏岗,邓冰,杜辉,武军林.过山脊内孤立波演变及其对细长潜体的作用力特性.力学学报,2017,49(6):1260-1271

Gu Mengmeng,Wei Gang,Deng Bing,Du Hui,Wu Junlin.Experimental investigation on the evolution of internal solitary wave over a ridge and its acting forces on a submerged slender body.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1260-1271