强安全的匿名隐式漫游认证与密钥协商方案

陈 明

(宜春学院数学与计算机科学学院 江西宜春 336000) (可信计算与信息保障国家重点实验室(中国科学院软件研究所) 北京 100190)

强安全的匿名隐式漫游认证与密钥协商方案

陈 明

(宜春学院数学与计算机科学学院 江西宜春 336000) (可信计算与信息保障国家重点实验室(中国科学院软件研究所) 北京 100190)

(chenming9824@aliyun.com)

现有两方漫游认证与密钥协商方案没有考虑抵抗临时秘密泄露的安全性，仅在CK模型下可证明安全.基于椭圆曲线密码体制和基于身份密码系统，采用Schnorr签名算法设计了类似HMQV方案的“挑战-应答”签名，进而构造了一种基于隐式认证技术的、具有强安全性和匿名性的两方漫游认证密钥协商方案.随后，扩展了ID-BJM模型，使之能模拟两方漫游认证与密钥协商方案.在扩展的安全模型下，新方案的安全性被规约为多项式时间敌手求解椭圆曲线上的计算Diffie-Hellman问题，实现了eCK安全.对比分析表明：新方案具有更强的安全性，能抵抗临时秘密泄露攻击，需要实现的密码算法更少，计算、通信和存储开销都相对较低.新方案可应用于移动通信网络、物联网或泛在网络中，为资源约束型移动终端提供安全的漫游接入服务.

认证密钥协商；移动漫游服务；基于身份密码系统；隐式认证；计算Diffie-Hellman问题；eCK模型

随着移动通信网与互联网的融合，在生活领域，各种手持设备和穿戴传感设备已经大量为人们所使用；在生产领域，以RFID技术和传感器技术为代表的低能耗设备也已广泛应用，新型的网络形态(物联网或泛在网络)正在逐步形成.新型网络的一个典型特征是终端设备多样化和移动频繁.为适应不同设备的安全需求，多样化的网络安全技术研究是目前网络通信和信息安全领域的一个主流趋势，针对资源受限移动设备的漫游接入认证与密钥协商方案是近年来的一个研究热点[1].

由于早期的移动终端计算能力低下，漫游协议主要采用三方在线认证的方式[2-6]，不使用公钥算法.在认证过程中，首先由移动节点(mobile node, MN)将认证消息发送给远程域认证服务器(foreign server, FS)，然后FS将认证消息转发给MN的家乡服务器(home server, HS)，由HS在线验证MN的身份，并将认证结果返回给FS.三方漫游协议具有较大的通信时延，且易于遭受DOS攻击.

随着移动设备计算和存储能力的提升，如今大量的移动终端能够很好地支持公钥加密算法，一些研究者基于公钥算法，提出两方的漫游认证协议[7-14]，其具体优点是不需要HS在线参与认证.在最近提出的6种两方漫游认证方案中，Jo等人[9]方案采用加密Hash链表存储MN的撤销信息，降低了节点撤销过程中的通信开销，采用基于身份的签密方案[15]实现了匿名认证，并且在CK模型[16]下证明了协议的安全性；Tsai等人[10]改进了Jo等人方案，采用了新的基于身份签密方案，降低了计算、通信和存储开销，并且在服务器端使用了基于身份的批量签名验证技术，支持用户身份的批量验证，进一步降低认证服务器的计算开销；周彦伟等人[11-13]提出3种相近的漫游认证方案，采用公钥加密和数字签名技术实现漫游匿名认证，采用Diffie- Hellman密钥交换机制实现密钥协商；此外，胡志华等人[14]采用代理签名实现了两方的漫游认证，但是没有实现密钥协商.

上述两方漫游认证与密钥协商方案存在3点不足：

1) 文献[9-13]提出的方案安全性较弱，在CK模型下可证明安全(Tsai方案采用了类似的模型)，没有考虑会话临时秘密泄露攻击.由于移动设备更容易被攻击者劫持，进而读取其内存信息，导致认证会话状态信息泄露，形成会话临时秘密泄露攻击.

2) 现有方案的计算和存储开销较大，移动节点需要支持的公钥算法类型较多.例如文献[9-11,13]的方案采用了双线性映射群，引入了计算代价较高的双线性对运算，周彦伟等人[11-13]方案在漫游认证阶段使用了多次公钥加密和数字签名算法，这些都增加了方案的计算开销和算法实现方面的成本.目前虽然移动终端能够有效支持公钥算法，但是其总体的计算能力仍然较低且能量有限，特别是一些微型的传感器设备，仅能支持简单的公钥算法[17].

3) 文献[9-13]提出的方案均要求移动节点预先存储远程认证服务器的身份ID(或公钥)，增加了移动节点的存储开销，并且影响了节点漫游的自由度(移动节点要么预先存储所有远程域认证服务器的公钥，要么只能在局部区域漫游).

通过上述分析可见，更加高效和安全的两方漫游认证与密钥协商方案仍然需要进一步研究，这是本文研究工作的动机.

本文基于椭圆曲线密码体制(elliptic curve cryp-tography, ECC)和基于身份密码系统[18-19](identity-based cryptosystem, IBC)，设计了一种高效且强安全的两方漫游认证与密钥协商方案.新方案在扩展的ID-BJM模型[20-21]下被证明实现了eCK[22]安全性，其安全性被规约为多项式时间敌手求解椭圆曲线上的计算Diffie-Hellman(CDH)问题.

本文研究工作主要有2点创新点：1)采用类似HMQV[23]方案的隐式认证技术实现了移动节点与远程域认证服务器之间的相互认证和密钥协商；2)在文献[20-21]的基础上，进一步扩展了ID-BJM模型用于分析移动漫游认证协议，并且实现了模拟该类协议的eCK安全性.HMQV隐式认证技术的优点在于，所有公开发送的认证会话消息都不包含任何形式的用户长期私钥信息，并且所有公开的认证会话消息都不需要进行加密或签名，相互认证的实现取决于认证双方能够计算完全一致的会话密钥.相较现有方案，本文方案有3个主要的优点：

1) 安全性更强，能抵抗临时秘密泄露攻击，能有效防止临时秘密泄露造成的移动节点认证私钥泄露；

2) 需要实现的算法库更少，计算、通信和存储开销都相对较低(这里算法库是指编程实现相关密码算法的函数库，例如实现双线性对运算的PBC Library[24])；

3) 移动节点不需要预先存储远程域认证服务器的ID和公钥，降低了存储开销，移动节点的漫游路线更加自由.

1 背景知识

1.1 困难数学问题

设G为椭圆曲线上的q阶循环群，P,Q∈G是曲线上的点，Q是P的倍数点，存在a∈q，满足：Q=aP.下面定义G上的CDH问题和CDH假设.

1) CDH问题.对于任意未知的a,b∈q，假设P∈G是G的生成元，给定(aP,bP)，计算abP.

2) CDH假设.不存在概率多项式时间算法能成功求解CDH问题.

说明：为了描述简洁，本文忽略了modq运算.

1.2 漫游认证模型

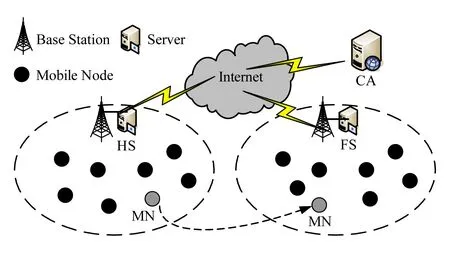
Fig. 1 Roaming authentication model图1 漫游认证模型

本文漫游认证方案的基本模型如图1所示，包含4个角色：证书权威(CA)、家乡域认证服务器HS、远程域认证服务器FS和移动节点MN.CA负责HS和FS的密钥分发与身份管理，HS负责MN的密钥分发与身份管理，FS为MN提供漫游接入服务.

漫游认证与密钥协商方案包含：系统建立、域服务器注册、节点注册、漫游接入认证4个算法.

1) 系统建立.输入安全参数κ，由CA产生并发布系统公开参数.

2) 域服务器注册.域服务器向CA中心进行注册，提交其身份标识，CA产生服务器私钥，并通过安全信道返回给相应的域服务器.

3) 节点注册.MN提交其身份标识，HS为MN产生临时身份和漫游时的认证私钥，通过安全信道返回给MN.

4) 漫游接入认证.当MN漫游进入其他认证域，该认证域的FS与MN进行交互，认证彼此身份，并协商一致的会话密钥.

1.3 漫游认证安全模型

eCK[22]模型是本领域被广泛引用的强安全模型之一，能模拟认证协议的主要安全性包括：已知会话密钥安全(known key security, KKS)、无密钥控制(no key control, NKC)、抗未知密钥共享(unknown key-share resilience, UKS)、弱的完美前向安全(weak perfect forward secrecy, wPFS)、抗密钥泄露伪装(key-compromise impersonation resilience, KCI)、抗临时秘密泄露安全(ephemeral secrets reveal resistance, ESR).此外，漫游认证还要求实现匿名性(anonymity).

本文采用基于身份的密码方案[18]构造漫游认证协议，因此，本文安全模型以ID-BJM模型[20]为基础，扩展定义了能实现eCK安全的ID-eCK模型，并用于分析漫游协议.下面简要描述相关概念及定义，详细内容见本文3.2节，或参考文献[20-21].

安全模型被定义为挑战者C与敌手A之间的一系列游戏Game.A被模拟为一个概率多项式时间图灵机，被允许执行多项式时间的询问(询问的具体内容见3.2节)，C模拟协议的相应算法做出应答.预言机Πu定义为A发起的第u次会话实例，会话的标识由用户标识和会话参数连接而成.Πu与Πv互为匹配预言机定义为：Πu与Πv具有相同的会话标识.在询问过程中，A提交对新鲜预言机Πt的Test询问，C输出一个会话密钥作为应答.最后，A输出对该密钥的猜测b′∈{0,1}，b′=0表示该密钥是Πt的真实密钥，否则不是.如果猜测正确，A赢得游戏Game.A赢得Game的优势定义为

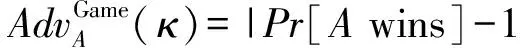
定义1. 新鲜性(freshness).如果Πt是诚实用户IDa和IDb之间的会话，IDa是Πt的拥有者，且Πt已成功完成(用Acc表示)，令Πv(如果存在)是Πt的匹配预言机，那么，分别定义3种类型的新鲜预言机Πt：

1)A从未提交Corrupt(IDb)，Reveal(Πt)，Reveal(Πv)，EpheKeyReveal(Πt)询问；

2)A从未提交Reveal(Πt)，Reveal(Πv)，EpheKeyReveal(Πv)，EpheKeyReveal(Πt)询问；

3)A从未提交Corrupt(IDa)，Corrupt(IDb)，Reveal(Πt)，Reveal(Πv)询问.

上述3种情形涵盖了认证密钥协商协议的主要安全问题，类型1模拟KCI安全；类型2模拟wPFS安全性；类型3模拟ESR安全性.其他安全性更易于实现，如KKS和NKC，由会话双方各自选择的新鲜随机数确保；UKS安全性(类似Diffie-Hellman密钥交换的中间人攻击)则由隐式认证技术保障，因为对认证会话消息的任何篡改都会导致认证双方不能计算一致的会话密钥，从而认证失败.

定义2. 如果协议满足2点要求，被认为满足eCK安全：

1) 在匹配预言机Πu与Πv之间仅存在被动攻击者的情况下，总能协商相同的会话密钥SK，且SK在密钥空间上随机均匀分布；

2 漫游认证与密钥协商协议

基于ECC的IBC系统设计了一种采用隐式认证技术的漫游认证与密钥协商协议.本文协议只涉及漫游认证，但是稍加变化也可用作家乡域的本地认证.

在CK模型下，Fiore等人[25]提出一种高效的基于身份密钥协商方案(记为Fiore-IBKA方案)，但是该方案没有考虑临时密钥泄露的攻击.文献[26]指出Fiore-IBKA方案易遭受临时密钥泄露伪装攻击.本文方案受到Fiore-IBKA方案的启发，结合Schnorr[27]签名机制设计了类似HMQV方案的“挑战-应答”签名，进而构造了高效且强安全的匿名漫游认证与密钥协商方案.本文方案描述如下.

1) 系统建立.输入安全参数κ，CA产生并发布系统参数params=〈κ,G,q,P,P0,H1,H2,H3〉.其中q为大素数，P∈G为G的生成元，P0=sP为系统公钥，s∈q为主密钥，H1：{0,1}*→q和H2：{0,1}*→q为抗碰撞Hash函数，H3：{0,1}*→{0,1}κ为密钥导出函数.

2) 域服务器注册.域服务器提交其身份标识IDS，CA随机选择rS∈q，计算RS=rSP，qS=H1(IDS‖RS)和dS=rS+sqS，通过安全信道将〈dS,RS〉发回给域服务器.域服务器通过计算dSP=RS+qSP0是否相等来验证私钥的正确性.私钥产生算法采用了Schnorr签名机制，IDS为被签名消息.

3) 节点注册.MN提交其身份标识IDM，HS随

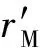
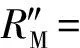
4) 漫游接入认证.漫游接入认证过程如图2所示：

MNFSx∈ZZq，X=xPX‖CertM→True←Verify(CertM)y∈ZZq，Y=yPqF=H1(IDF‖RF)TM=xYY‖IDF‖RF←qH=H1(IDH‖RH)TF=yXh=H2(IDF‖CertM‖RF‖RM‖X‖Y)KF=(y+hdF)(X+h(RM+tIDM(RH+qHP0)))KM=(x+hdM)(Y+h(RF+qFP0))SKFM=H3(IDF‖tIDM‖X‖Y‖h‖TF‖KF)SKMF=H3(IDF‖tIDM‖X‖Y‖h‖TM‖KM)

Fig. 2 Authentication and key agreement for roaming service图2 漫游认证与密钥协商

认证步骤描述为：

① MN随机选择x∈q，计算X=xP，发送(X‖CertM)给FS.

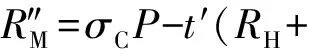
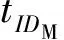
上述过程是基本的认证密钥协商方案(没有考虑密钥确认)，采用了类似HMQV的隐式认证技术.考虑到实际应用中需要进行密钥确认，我们对上述基本方案在4个方面进行增强，具体描述如下：

1) 系统建立阶段引入抗碰撞密码Hash函数H：K×{0,1}*→q；

2) FS将h同时发送给MN，即FS发送消息(Y‖IDF‖RF‖h)；

3) MN检查h=H2(IDF‖CertM‖RF‖RM‖X‖Y)是否成立，计算g=H(SKMF‖IDF‖CertM‖RF‖RM‖X‖Y‖h)，并发送给FS；

4) FS检查g=H(SKFM‖IDF‖CertM‖RF‖RM‖X‖Y‖h)是否成立以完成密钥确认.

3 分析与比较

3.1 协议正确性分析

协议的正确性证明：

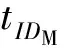
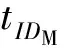
(y+hdF)(x+hdM)P，

(1)

KM=(x+hdM)(Y+h(RF+qFP0))=

(x+hdM)(y+h(rF+sqF))P=

(x+hdM)(y+hdF)P.

(2)

由式(1)和式(2)可得KF=KM，从而可计算相同的会话密钥SKFM=SKMF.

3.2 协议安全性分析

本文第2节描述的基本方案(不考虑密钥确认)更加符合HMQV协议的思想，为了便于分析和证明，在下面的证明过程中，我们仅分析基本的认证密钥协商方案(非增强版本).

定理1. 假设仅存在被动攻击者的情况下，相互匹配的预言机Πu与Πv总能协商一致的会话密钥SK，且SK在密钥空间上随机均匀分布.

证明. 假设A是被动攻击者，则预言机Πu/Πv总能正确接收彼此输出的消息.根据3.1节的结论，Πu和Πv能计算相同的会话密钥SKMF=SKFM.且由于x和y是IDM和IDF随机选择的临时秘密，那么(TM,KM)和(TF,KF)可看成是随机生成，SKMF/SKFM根据(TM,KM)/(TF,KF)由密钥导出函数生成，因此，SKMF/SKFM在密钥空间上随机均匀分布.

证毕.

定理2. 假设H1/H2/H3模拟随机预言机，如果CDH假设成立，那么本文协议满足eCK安全.

证明. 根据本文1.3节定义的安全模型，我们将协议的安全性规约到求解CDH问题.假如存在多项式时间敌手A以优势ε(κ)赢得下面构造的挑战-测试游戏，那么可以构造算法以不低于f(ε(κ))的概率求解CDH问题.

考虑到漫游认证协议的特殊性，该类协议是非对称的认证密钥协商协议，协议的发起者(MN)和响应者(FS)角色是固定的，不能互换.因此，我们进一步扩展ID-BJM模型[20-21]，考虑4种情况证明漫游认证协议满足eCK安全.注意:本文用i专指发起者，用j专指响应者,令sid*是挑战会话，

1)sid*不存在匹配会话，且拥有者为i.①事件E1，A不能询问j的长期私钥和sid*的临时私钥；②事件E2，A不能询问i和j的长期私钥.

2)sid*不存在匹配会话，且拥有者为j.①事件E3，A不能询问i的长期私钥和sid*的临时私钥；②事件E4，A不能询问i和j的长期私钥.

3)sid*存在匹配会话sid′，且拥有者为i.①事件E5，A不能询问sid*和sid′的临时私钥；②事件E6，A不能询问i和j的长期私钥；③事件E7，A不能询问j的长期私钥和sid*的临时私钥.

4)sid*存在匹配会话sid′，且拥有者为j.①事件E8，A不能询问sid*和sid′的临时私钥；②事件E9，A不能询问i和j的长期私钥；③事件E10，A不能询问i的长期私钥和sid*的临时私钥.

上述事件分为sid*是否存在匹配会话两大类，其中，E1，E3，E7，E10模拟KCI安全性，E2，E4，E6，E9模拟ESR安全性，E5，E8模拟wPFS安全性.我们通过一系列的挑战-测试游戏模拟上述事件.

游戏模拟过程中，我们引入一个判定预言机O(#,#)判定O(xP,yP)=O(W,P)是否成立.采用双线性对[19-20]运算可构造此预言机，因此我们要求在协议模拟过程中，系统参数满足双线性映射条件.这一要求与协议本身无关，且不影响安全性，因为在满足双线性映射条件的群G上CDH假设也是成立的.

假设至多创建了m个移动节点、n个认证服务器以及l次会话，sid*是挑战会话.

Game1. 给定CDH问题实例(aP,bP)，求解abP.

初始化：挑战者C生成系统公开参数params=〈κ,G,q,P,P0,H1,H2,H3〉，其中P0=aP，H1/H2/H3模拟为随机预言机.C随机选择∈{1,2,…,l}和j**∈{j1,j2,…,jn}.

询问：C维护初始为空的列表LID，L2，L3，LS，按以下方式对A的询问做出应答.

H1(ID,#).如果ID在LID中存在，则输出tID，否则C随机选择并输出tID∈q.

1) 如果ID=j**，C随机选择rID∈q，计算RID=rIDP，设置fID=FS，将〈fID,ID,RID,rID,tID,⊥〉插入LID；

2) 否则C随机选择dID∈q，计算RID=dIDP-tIDP0，设置fID=FS，将〈fID,ID,RID,⊥,tID,dID〉插入LID.

其中，fID为用户身份标签，fID=FS表示域认证服务器，fID=MN表示移动节点，⊥表示空值.

H2(j,i,Rj,Ri,X,Y).如果〈j,i,Rj,Ri,X,Y,h〉在L2中存在，则输出h；否则，C随机选择h∈q，输出h，将〈j,i,Rj,Ri,X,Y,h〉插入L2.注意，为了简化符号标识，这里直接使用用户标识i代替了其证书Certi.

H3(j,i,X,Y,h,T,K).如果〈j,i,X,Y,h,T,K,SK〉在L3中存在，C直接输出SK；否则存在3种情况：

1) 如果存在〈j,i,X,Y,h,⊥,K,SK〉，此时j=j**且LS中不存在发起者预言机(见Send1询问)，C调用判定预言机判定O(X,Y)=O(T,P)是否成立，若成立，则更新该记录为〈j,i,X,Y,h,T,K,SK〉，并且用T更新LS中的相应记录，否则，随机选择SK←{0,1}k，将〈j,i,X,Y,h,T,K,SK〉插入L3，输出SK；

2) 如果存在〈j,i,X,Y,h,T,⊥,SK〉，此时j=j**∧X=ηbP(见Send1询问)，更新记录为〈j,i,X,Y,h,T,K,SK〉，用K更新LS中的相应记录，输出SK；

3)C查询L2，如果L2中存在相应元组〈j,i,Rj,Ri,X,Y,h〉，那么随机选择并输出SK←{0,1}k，将〈j,i,X,Y,h,T,K,SK〉插入L3；否则忽略该询问；

4) 以〈j,i,X,Y,h,T,K〉为索引在LS中查询，若存在相应记录，且已输出SK，则将该会话标记为Revealed.

Create(ID).如果ID是认证服务器，C执行H1询问；如果ID是移动节点，C执行H1询问，创建家乡服务器公私钥〈IDH,RH,tH,dH〉，随机选择rID,tID∈q，计算dID=rID+tIDdH，RID=rIDP，生成公钥证书CertID，将〈MN,ID,RID,rID,tID,dID,CertID〉插入LID.

Send0(Πu,I,i,j).A发起了1次新的会话，i为发起者，j为响应者，C创建发起者预言机Πu(I表示会话的发起者角色).如果u=，且j=j**(否则终止游戏)，C随机选择η∈q，令X=ηbP，将〈Πu,I,i,j,η,X,#〉插入LS；否则，C随机选择x∈q，计算X=xP，将〈Πu,I,i,j,x,X,#〉插入LS.输出(X‖Certi).

Send1(Πv,R,j,i,(X‖Certi)).C验证Certi，如果验证错误，则忽略该询问；否则创建响应者预言机Πv(R表示会话的响应者角色).C随机选择y,h∈q和SK←{0,1}k，计算T=yX，

1) 如果j≠j**，计算Y=yP和K=(y+hdj)(X+hdiP))，将〈Πv,R,j,i,X,y,Y,h,T,K,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,K,SK〉插入L3；

2) 如果j=j**∧X=ηbP，计算Y=yP，将〈j,i,X,Y,h,T,⊥,SK〉插入L3，将〈Πv,R,j,i,X,y,Y,h,T,⊥,SK,Acc〉插入LS；

3) 如果j=j**且已创建Πu(u≠)与之匹配，计算Y=yP和K=(x+hdi)(Y+h(Rj+tjP0))，将〈Πv,R,j,i,X,y,Y,h,T,K,SK,Acc〉插入LS，〈j,i,X,Y,h,T,K,SK〉插入L3；

4) 如果j=j**且不存在Πu与之匹配，计算Y=yP-h(Rj+tjP0)和K=y(X+hdiP)，将〈Πv,R,j,i,X,y,Y,h,⊥,K,SK,Acc〉插入LS，将〈j,i,X,Y,h,⊥,K,SK〉插入L3；

5) 将〈j,i,Rj,Ri,X,Y,h〉插入L2，输出(Y‖j‖Rj).

Send2(Πu,I,i,j,X,(Y‖j‖Rj)).

1) 如果u=，C执行H2询问取得h，更新状态为〈Πu,I,i,j,η,X,Y,h,⊥,⊥,⊥,Acc〉；

2) 如果u≠，LS中同时存在〈Πv,R,j,i,X,y,Y,h,T,K,SK,Acc〉和Πu，更新Πu为〈Πu,I,i,j,x,X,Y,h,T,K,SK,Acc〉，如果不存在Πu，插入新的〈Πu,I,i,j,⊥,X,Y,h,T,K,SK,Acc〉；否则LS中存在Πu但不存在匹配的Πv，C计算T=xY和K=(x+hdi)(Y+h(Rj+tjP0))，执行H2/H3询问取得h，SK，更新记录为〈Πu,I,i,j,x,X,Y,h,T,K,SK,Acc〉；否则，Πu以及与其匹配的Πv均未创建，则忽略该询问.

Reveal(sid).如果sid≠sid*在LS中已存在，且状态为Acc，则输出相应的SK，并标记sid为Revealed；否则输出⊥.

Corrupt(ID).输出ID的长期私钥dID.注意，A不能询问ID=j**的长期私钥.

EpheKeyReveal(sid).输出sid的临时私钥x(sid的拥有者为i)或y(sid的拥有者为j).注意，A不能询问sid*的临时私钥.

Test(sid*).令sid*=〈Π,I,i*,j*,X*,Y*〉，如果j*≠j**或存在已Revealed的会话sid′与sid*相匹配，那么终止游戏.否则C输出随机的SK*←{0,1}k.

Test询问结束以后，A可以继续执行Test以外的询问，但不能破坏挑战预言机的新鲜性.最后，A返回其猜测位b′∈{0,1}.

上述模拟过程包含2类事件E1和E7.

事件E1.LS中不存在sid′与sid*相匹配，C从L3中随机选择(T*,K*)，计算abP=(K*-T*-h*r*jX*-h*d*i(Y*+h*(R*j+t*jP0)))/ηh*t*j，作为对CDH挑战的回答.其中，X*=ηbP，j*=j**，(d*i,r*j,R*j,t*j)从LID中取得，以下相同.

事件E7.LS中存在sid′与sid*相匹配，C从L3中随机选择K*，计算abP=(K*-(y*+h*r*j)X*-h*d*i(Y*+h*(R*j+t*jP0)))/ηh*t*j，作为对CDH挑战的回答.其中，y*从会话sid′中取得.

所有的预言机模拟器有效，其输出消息在消息空间上均匀分布，A不能发现模拟过程与真实攻击之间的差异.

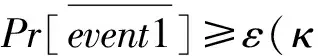
引理1的论述与文献[20]中Claim 2类似.假设H1/H2/H3模拟随机预言机，如果event1发生，那么，A只可能在2种情况下赢得Game1：

1)A随机猜测SK*是否是sid*的真实会话密钥；

2)A知道某个已Revealed的会话sid″与sid*具有相同的会话密钥.

也就是说，C在没有察觉的情况下响应了针对sid″的H3询问.根据H3询问过程，C对具有相同输入的H3询问做出相同的应答.如果sid″与sid*具有相同会话密钥，则：要么sid″=sid*，要么sid″与sid*相匹配.根据游戏规则，sid*及其匹配会话不允许被Revealed.因此，情形2发生的概率至多为1/2κ(H3的输出发生碰撞的概率).那么：Pr[Awins|event1]≤1/2，

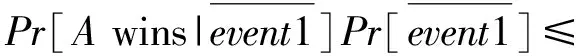
如果游戏没有终止，A选择了第次会话作为挑战，且j=j**，记为event2.那么：Pr[event2]≥1/n·l.

令event3表示C找到了正确的(T*,K*)(E1)或K*(E7)，那么C成功的概率为

其中，q3表示L3中记录的数量.

Game2. Game2模拟事件E3，E10，其模拟过程与Game1相似，下面主要描述与Game1不同之处.

初始化：按照协议生成系统参数params，其中，P0=sP，s∈q，C选择∈{1,2,…,l}和i**∈{i1,i2,…,im}.

询问：H1(ID,#).如果ID在LID中存在，则输出tID，否则C随机选择并输出tID∈q，然后按照协议计算认证服务器的私钥，并维护LID.

H2(j,i,Rj,Ri,X,Y).与Game1相同.

H3(j,i,X,Y,h,T,K).与Game1基本相同.不同之处在于：当i=i**，如果存在〈j,i,X,Y,h,T,⊥,SK〉，令Q=(K-T-hxdjP-h2dj(Ri+tiP0))/h，C判定O(Y,aP)=O(Q,P)是否成立，若成立，则更新记录为〈j,i,X,Y,h,T,K,SK〉，用K更新LS中相应记录，否则随机选择SK←{0,1}k，将〈j,i,X,Y,h,T,K,SK〉插入L3.

Create(ID).与Game1基本相同.不同之处：如果ID=i**，C随机选择tID∈q，执行H1询问取得dH，计算RID=tIDdHP-aP，然后生成公钥证书CertID，将〈MN,ID,RID,⊥,tID,⊥,CertID〉插入LID.

Send0(Πu,I,i,j).C随机选择x∈q，计算X=xP，将〈Πu,I,i,j,x,X,#〉插入LS，输出(X‖Certi).

Send1(Πv,R,j,i,(X‖Certi)).C创建Πv，

1) 如果v=∧i=i**，C随机选择η∈q，令Y=ηbP，执行H2询问取得h，若LS中存在Πu，计算T=xY，将〈Πv,R,j,i,X,η,Y,h,T,⊥,⊥,Acc〉插入LS，若不存在Πu，则将〈Πv,R,j,i,X,η,Y,h,⊥,⊥,⊥,Acc〉插入LS；

2) 否则，随机选择y∈q，计算Y=yP，T=yX，执行H2询问取得h，计算K=(y+hdj)(X+h(Ri+tiP0)))，随机选择SK←{0,1}k，将〈Πv,R,j,i,X,y,Y,h,T,K,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,K,SK〉插入L3；

3) 输出(Y‖j‖Rj).

Send2(Πu,I,i,j,X,(Y‖j‖Rj)).与Game1基本相同.不同之处：①不存在u=情形；②如果i=i**，LS中存在Πu但不存在Πv与之匹配，C执行H2询问取得h，计算T=xY，若L3中存在〈j,i,X,Y,h,T,K,SK〉，令Q=(K-T-hxdjP-h2dj(Ri+tiP0))/h，判定O(Y,aP)=O(Q,P)成立则更新记录为〈Πu,I,i,j,x,X,Y,h,T,K,SK,Acc〉，否则随机选择SK←{0,1}k，更新记录〈Πu,I,i,j,x,X,Y,h,T,⊥,SK,Acc〉，将〈j,i,X,Y,h,T,⊥,SK〉插入L3.

Reveal(sid).与Game1相同.

Corrupt(ID).输出ID的长期私钥dID.注意，A不能询问i=i**的长期私钥.

EpheKeyReveal(sid).与Game1相同.

Test(sid*).与Game1基本相同.不同的是sid*的拥有者为响应者预言机，且i*=i**.

最后，A返回其猜测位b′∈{0,1}.

事件E3.C从L3中随机选择(T*,K*)，计算abP=(K*-T*-h*d*jX*-h*2d*jaP)/ηh*，作为对CDH挑战的回答.

事件E10.C从L3中随机选择K*，计算abP=(K*-(x*+h*d*j)Y*-h*2d*jaP)/ηh*，作为对CDH挑战的回答.

与Game1类似，C成功的概率为

Pr[Cwins]≥(1/m×l×q3)ε(κ).

Game3. Game3模拟事件E2，E6，其模拟过程与Game1和Game2相似.

初始化：与Game2相同，C选择∈{1,2,…,l}，i**∈{i1,i2,…,im}，以及j**∈{j1,j2,…,jn}.

询问：H1(ID,#).与Game2基本相同.不同之处：如果ID=j**，则计算RID=tIDsP-bP.

H2(j,i,Rj,Ri,X,Y).与Game1相同.

H3(j,i,X,Y,h,T,K).与Game1基本相同.不同之处：如果L3中存在〈j,i,X,Y,h,T,⊥,SK〉，

1) 当i=i**，令Q=K-T-hxbP，判定O(Y+hbP,haP)=O(Q,P)是否成立；当j=j**，令Q=K-T-hyaP，判定O(X+haP,hbP)=O(Q,P)是否成立；

2) 如果上述判定等式成立，则更新记录为〈j,i,X,Y,h,T,K,SK〉，用K更新LS中相应记录；否则随机选择并输出SK←{0,1}k，在L3中插入新的〈j,i,X,Y,h,T,K,SK〉.

Create(ID).与Game2相同.

Send0(Πu,I,i,j).与Game2相同.

Send1(Πv,R,j,i,(X‖Certi)).C创建Πv，随机选择y∈q和SK←{0,1}k，计算Y=yP，T=yX，执行H2询问取得h，输出(Y‖j‖Rj).

1) 如果i=i**∧j=j**，将〈Πv,R,j,i,X,y,Y,h,T,⊥,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,⊥,SK〉插入L3；(这里对事件E2作特殊处理)如果挑战会话Π已更新状态为〈Π,I,i**,j**,x*,X*,Y*,h*,T*,⊥,⊥,Acc〉，其中，Y*=y*P是Send2询问的输入消息，由敌手产生，对C来说，y*未知，且如果LS中存在〈Πu,I,i**,j**,x,X,#〉，那么C随机选择η∈q，计算Y=ηY*，T=xηY*，将〈Πv,R,j,i,X,η,Y,h,T,⊥,SK,Acc〉插入LS，〈j,i,X,Y,h,T,⊥,SK〉插入L3；

2) 如果i≠i**∧j=j**，存在匹配的Πu，计算K=(x+hdi)(Y+hbP)，将〈Πv,R,j,i,X,y,Y,h,T,K,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,K,SK〉插入L3；如果不存在Πu，将〈Πv,R,j,i,X,y,Y,h,T,⊥,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,⊥,SK〉插入L3；

3) 如果j≠j**，计算K=(y+hdj)(Y+hPi)，其中，Pi表示i的公钥，将〈Πv,R,j,i,X,y,Y,h,T,K,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,K,SK〉插入L3.

Send2(Πu,I,i,j,X,(Y‖j‖Rj)).与Game1基本相同，不同之处在于，C计算T=xY，执行H2询问取得h：

1) 如果u=，且i=i**∧j=j**，更新状态为〈Πu,I,i,j,x,X,Y,h,T,⊥,⊥,Acc〉；

2) 如果i=i**(但u≠)且LS中不存在匹配的Πv，如果L3中存在〈j,i,X,Y,h,T,K,SK〉，令Q=K-T-hxbP，若判定O(Y+hbP,haP)=O(Q,P)成立，则更新记录为〈Πu,I,i,j,x,X,Y,h,T,K,SK,Acc〉，否则随机选择SK←{0,1}k，将〈Πu,I,i,j,x,X,Y,h,T,⊥,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,⊥,SK〉插入L3.

Reveal(sid).与Game1相同.

Corrupt(ID).输出ID的长期私钥dID.注意，A不能询问i=i**和j=j**的长期私钥.

EpheKeyReveal(sid).输出sid的临时私钥.

Test(sid*).与Game1基本相同.不同的是：i*=i**∧j*=j**；且对于事件E2，C查找〈j**,i**,X′,Y′,h′,T′,K′,SK′〉，其中Y′=ηY*(见Send1询问)，如果该记录存在，且K′≠⊥，则继续，否则终止游戏.

最后，A返回其猜测位b′∈{0,1}.

事件E2.C从L3中随机选择K*，并取得K′，令：

y*aP=(K′-ηx′Y*-h′x′bP-h′2abP)/ηh′，

K*=x*Y*+h*x*bP+h*y*aP+h*2abP.

2个等式合并求解：

abP=

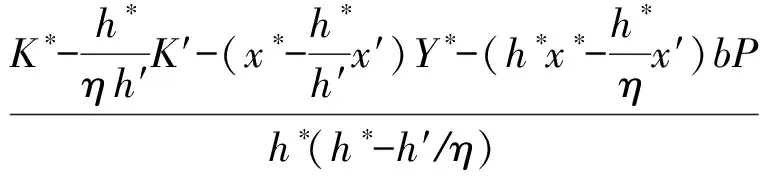
作为对CDH挑战的回答.

事件E6.C从L3中随机选择K*，计算abP=(K*-T*-h*x*bP-h*y*aP)/h*2，作为对CDH挑战的回答.

与Game1类似，C成功的概率为

Pr[Cwins]≥(1/m×n×l×q3)ε(κ).

说明.上述模拟过程中，对事件E2的特殊处理是因为Y*=y*P由敌手产生，C无法同时求解2个CDH问题实例(y*P,aP,y*aP)和(aP,bP,abP).通过上述方式，让敌手提供其中一个解y*aP.

Game4. Game4模拟事件E4,E9，其模拟过程与Game3基本一致，不同之处是挑战会话的拥有者为j**，这里不再详述.对于事件E4，采用与E2相同的方式处理.

Game5，Game6分别模拟事件E5，E8，其模拟过程与Game1～Game4类似，Game5，Game6的区别在于挑战会话的拥有者不同.

Game5. 初始化：与Game2相同，C选择,γ∈{1,2,…,l}，且≠γ.

询问：H1(ID,#).与Game2相同.

H2(j,i,Rj,Ri,X,Y).与Game1相同.

H3(j,i,X,Y,h,T,K).如果〈j,i,X,Y,h,T,K,SK〉在L3中存在，C直接输出SK；否则，随机选择SK←{0,1}k，将〈j,i,X,Y,h,T,K,SK〉插入L3，输出SK.

Create(ID).与Game2相同.

Send0(Πu,I,i,j).与Game1基本一致.不同之处：挑战会话不要求j=j**.

Send1(Πv,R,j,i,(X‖Certi)).C创建Πv，

1) 如果v=γ，且X=ηbP(否则终止游戏)，C随机选择μ∈q，令Y=μaP，执行H2询问取得h，将〈Πv,R,j,i,X,μ,Y,h,⊥,⊥,⊥,Acc〉插入LS，同时更新Π为〈Π,I,i,j,η,X,Y,h,⊥,⊥,⊥,Acc〉；

2) 否则，随机选择y∈q和SK←{0,1}k，计算Y=yP，执行H2询问取得h，计算K=(y+hdj)(X+hdiP)，T=yX，将〈Πv,R,j,i,X,y,Y,h,T,K,SK,Acc〉插入LS，将〈j,i,X,Y,h,T,K,SK〉插入L3；

3) 输出(Y‖j‖Rj).

Send2(Πu,I,i,j,X,(Y‖j‖Rj)).与Game1相同.

Reveal(sid).与Game1相同.

Corrupt(ID).输出ID的长期私钥dID.

EpheKeyReveal(sid).输出sid的临时私钥.A不能询问sid*及其匹配会话的临时私钥.

Test(sid*).与Game1基本相同，但不要求j*=j**.

最后，A返回其猜测位b′∈{0,1}.

事件E5.C从L3中随机选择(T*,K*)，计算abP=(K*-T*-h*dj*ηbP-h*di*μaP)/μη回答CDH挑战.

与Game1类似，C成功的概率为

Pr[Cwins]≥(1/l2×q3)ε(κ).

Game6. Game6与Game5基本一致，这里不再描述.

证毕.

3.3 匿名性分析

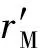
3.4 分析与比较

表1和表2对最近提出的5种两方漫游认证协议进行了对比分析.

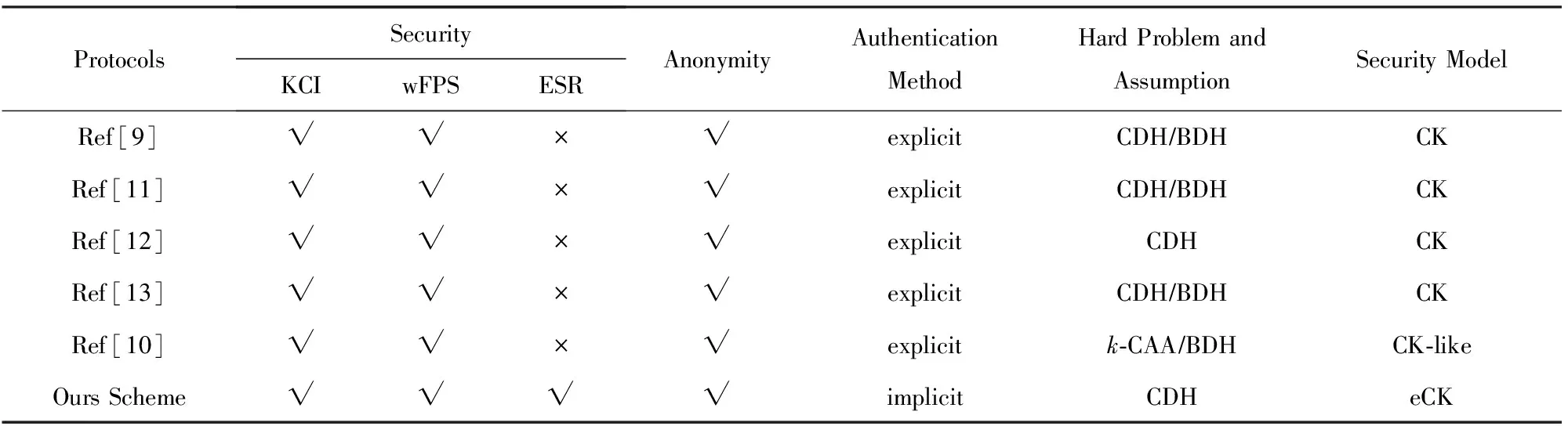
Table 1 Comparison of Security

Notes: “√” means the protocol achieves the security property; “×” means the protocol doesn’t achieve the security property.

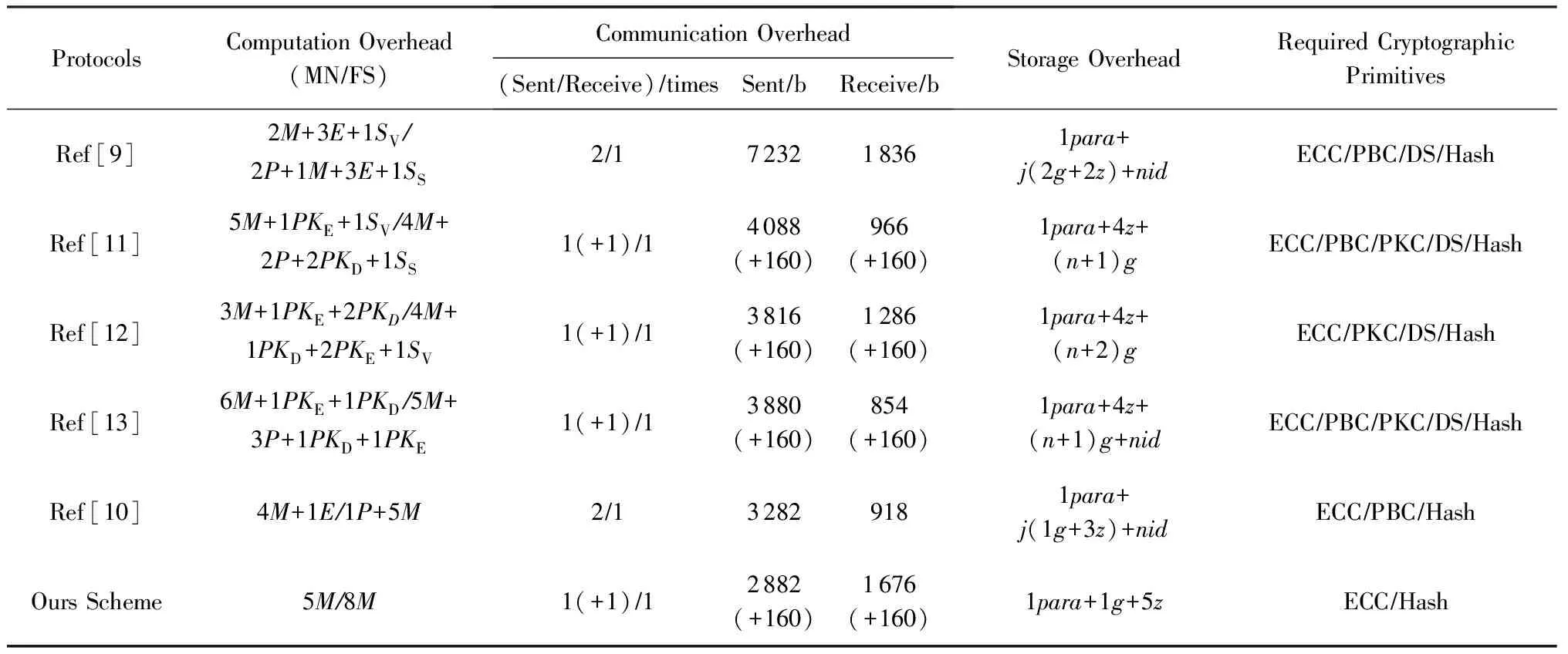
Table 2 Comparison of Protocols’ Performance

Notes:“M” represents a scalar multiplication inG. “E” represents an exponentiation inGT. “P” represents a pairing computation. “PKE” represents a public key encryption, and “PKD” represents a public key decryption. “SS” represents a digital signature, and “SV” represents verifying a signature. “para”, “z”, “g” and “id” represent a storage section occupied by system public parameters, an element inq, an element inG, and an identity, respectively. “ECC”, “PBC”, “PKC” and “DS” represent elliptic curve cryptography, pairing-based cryptography, public key cryptosystem, and digital signature scheme, respectively.

表2对比了相关协议的计算、通信和存储开销.以80 b安全等级为基准，参考文献[28]的实验数据，采用基于超奇异椭圆曲线上的有限域E(F2m)，q，G，GT上的元素分别为160 b，758 b，1 516 b.假定用户ID为20 B，时间数据为6 B.

由于各协议采用不同的系统参数，其中，Jo等人[9]协议、Zhou等人协议[11-13]和Tsai等人[10]协议采用双线性映射群，Zhou等人[11-13]协议使用了公钥加密和数字签名方案(未具体说明所采用的相关算法)，Jo等人协议使用了ECDSA方案，因此，很难做出完全一致的对比.总之，本文协议需要实现的算法库最少，计算、通信和存储开销均为最低.

计算方面，在MN端本文协议和Tsai协议相近，周彦伟等人提出的方案由于使用多次公钥加密和数字签名方案，计算量较高；在FS端本文协议开销最低，Tsai协议略高(根据基于MIRACL库的算法实现[28]，1P≈4M).

通信方面，列举了MN的通信开销(FS则相反)，所有协议实际都是发送2次/接收1次(带密钥确认，周彦伟等人协议忽略了密钥确认的步骤，为了保持一致性，采用类似本文的密钥确认方法，在发送和接收部分各增加160 b的密钥确认消息).总的通信开销对于智能手机差别不大，但是对于传感器节点还是有较大差别.以文献[17]的实验数据为基础，MICA2节点发送和接收1 B数据消耗能量分别约为52.2 μJ和19.3 μJ.总的通信能量消耗分别约为：23.6 mJ(本文协议)、23.7 mJ(Tsai协议)、28.9 mJ(Zhou协议)、29.5 mJ(Zhou协议)、30.5 mJ(Zhou协议)、52.6 mJ(Jo协议).

存储方面，本文协议需要的存储空间更少.周彦伟等人协议的漫游认证阶段第1个步骤，MN使用了FS的公钥加密消息，因此，需要预存FS的公钥(假设为n个)；Tsai协议和Jo协议每次漫游采用不同的临时身份和认证密钥(为了避免追踪)，需要预存j个认证密钥以及临时身份信息(j为最大的认证次数)，此外，该协议在第1步的计算中需要输入FS的ID，因此需要存储n个ID值；本文协议在步骤1的计算中不涉及FS的信息，FS的ID和公钥参数在步骤2中接收，无需预先存储，因此，本文协议仅需要存储公开参数、证书及私钥.根据3.3节的分析，为了实现不可追踪性，本文协议需要的存储空间为1para+j(1g+4z)+1z.

4 结束语

本文提出一种新的在移动漫游接入服务中的两方认证密钥协商方案.本文方案的特点是：所采用的公钥算法完全基于椭圆曲线上的点乘运算，对移动节点在算法支持方面的要求更低，计算、通信和存储开销也更低；采用了隐式认证技术，在实现匿名性的同时安全性更强，能抵抗临时秘密泄露的攻击；通过扩展，新方案能实现移动节点的不可追踪特性.此外，本文扩展了ID-BJM模型，使之能模拟两方漫游认证与密钥协商方案，并且使用扩展的ID-BJM模型证明了新方案达到eCK安全.

本文的漫游认证模型是建立在单一认证权威框架下的，具有全局统一的公开参数.对于多认证权威或者无全局认证权威(服务器对等模式)结构模型下的漫游认证方案还需要进一步研究.在该类网络结构中，不同的认证域拥有不同的系统参数，对密码算法的要求也不同，因此，对漫游认证方案的设计提出更高的要求.

[1]Zou Yulong, Zhu Jia, Wang Xianbin, et al. A survey on wireless security: Technical challenges, recent advances, and future trends[J]. Proceedings of the IEEE, 2016, 104(9): 1727-1765

[2] Jiang Yixin, Lin Chuang, Shen Xuemin, et al. Mutual authentication and key exchange protocols for roaming services in wireless mobile networks[J]. IEEE Trans on Wireless Communications, 2006, 5(9): 2569-2577

[3] Cao Chunjie, Yang Chao, Ma Jianfeng, et al. An authentication protocol for station roaming in WLAN mesh[J]. Journal of Computer Research and Development, 2009, 46(7): 1102-1109 (in Chinese)(曹春杰, 杨超, 马建峰, 等. WLAN Mesh漫游接入认证协议[J]. 计算机研究与发展, 2009, 46(7): 1102-1109)

[4] Wang Liangmin, Jiang Shunrong, Guo Yuanbo. Composable secure authentication protocol for mobile sensors roaming in the Internet of things[J]. Scientia Sinica: Informationis, 2012, 42(7): 815-830 (in Chinese)(王良民, 姜顺荣, 郭渊博. 物联网中移动Sensor节点漫游的组合安全认证协议[J].中国科学: 信息科学, 2012, 42(7): 815-830)

[5] Mun H, Han K, Lee Y S, et al. Enhanced secure anonymous authentication scheme for roaming service in global mobility networks[J]. Mathematical and Computer Modelling, 2012, 55(1/2): 214-222

[6] Shin S, Yeh H, Kim K. An efficient secure authentication scheme with user anonymity for roaming user in ubiquitous networks[J]. Peer-to-Peer Networking and Applications, 2015, 8(4): 674-683

[7] Yang Guomin, Huang Qiong, Wong D S, et al. Universal authentication protocols for anonymous wireless communi-cations[J]. IEEE Trans on Wireless Communications, 2010, 9(1): 168-174

[8] He Daojing, Chen Chun, Chan S, et al. Secure and efficient handover authentication based on bilinear pairing functions[J]. IEEE Trans on Wireless Communications, 2012, 11(1): 48-53

[9] Jo H J, Paik J H, Lee D H. Efficient privacy-preserving authentication in wireless mobile networks[J]. IEEE Trans on Mobile Computing, 2014, 13(7): 1469-1481

[10] Tsai J L, Lo N W. Provably secure anonymous authenti-cation with batch verification for mobile roaming services[J]. Ad Hoc Networks, 2016, 44: 19-31

[11] Zhou Yanwei, Yang Bo. Provable secure authentication protocol with direct anonymity for mobile nodes roaming service in Internet of things[J]. Journal of Software, 2015, 26(9): 2436-2450 (in Chinese)(周彦伟, 杨波. 物联网移动节点直接匿名漫游认证协议[J]. 软件学报, 2015, 26(9): 2436-2450)

[12] Zhou Yanwei, Yang Bo, Zhang Wenzheng. Secure and efficient roaming authentication protocol with controllable anonymity for heterogeneous wireless network[J]. Journal of Software, 2016, 27(2): 451-465 (in Chinese)(周彦伟, 杨波, 张文政. 安全高效的异构无线网络可控匿名漫游认证协议[J]. 软件学报, 2016, 27(2): 451-465)

[13] Zhou Yanwei, Yang Bo, Zhang Wenzheng. Controllable and anonymous roaming protocol for heterogeneous wireless network[J]. Acta Electronica Sinica, 2016, 44(5): 1117-1123 (in Chinese)(周彦伟, 杨波, 张文政. 异构无线网络可控匿名漫游认证协议[J]. 电子学报, 2016, 44(5): 1117-1123)

[14] Hu Zhihua, Liu Xiaojun. A roaming authentication protocol based on non-linear pair in IoT[J]. Journal of Sichuan University: Engineering Science Edition, 2016, 48(1): 85-90 (in Chinese)(胡志华, 刘小俊. 物联网中基于非线性对的漫游认证协议研究[J]. 四川大学学报: 工程科学版, 2016, 48(1): 85-90)

[15] Barreto P S L M, Libert B, McCullagh N, et al. Efficient and provably-secure identity-based signatures and signcryp-tion from bilinear maps[G] //LNCS 3788: Proc of ASIACRYPT 2005. Berlin: Springer, 2005: 515-532

[16] Canetti R, Krawczyk H. Analysis of key-exchange protocols and their use for building secure channels[G] //LNCS 2045: Advances in Cryptology — EUROCRYPT 2001. Berlin: Springer, 2001: 453-474

[17] Cao Xuefei, Kou Weidong, Dang Lanjun, et al. IMBAS: Identity-based multi-user broadcast authentication in wireless sensor networks[J]. Computer Communications, 2008, 31(4): 659-667

[18] Nehéz M, Olejár D, Demetrian M. On emergence of dominating cliques in random graphs[EB/OL]. 2008 [2016-09-01]. https://arxiv.org/abs/0805.2105

[19] Boneh D, Franklin M. Identity-based encryption from the weil pairing[G] //LNCS 2139: Proc of CRYPTO 2001. Berlin: Springer, 2001: 213-229

[20] Chen Liqun, Cheng Zhaohui, Smart N. Identity-based key agreement protocols from pairings[J]. International Journal of Information Security, 2007, 6(4): 213-241

[21] Chen Ming. Escrowable identity-based authenticated key agreement in the standard model[J]. Acta Electronica Sinica, 2015, 43(10): 1954-1962 (in Chinese)(陈明. 标准模型下可托管的基于身份认证密钥协商[J]. 电子学报, 2015, 43(10): 1954-1962)

[22] LaMacchia B, Lauter K, Mityagin A. Stronger security of authenticated key exchange[G] //LNCS 4784: Proc of the Int Conf on Provable Security (ProvSec 2007). Berlin: Springer, 2007: 1-16

[23]Krawczyk H. HMQV: A high-performance secure Diffie-Hellman protocol[G] //LNCS 3621: Advances in Cryptology — CRYPTO 2005. Berlin: Springer, 2005: 546-566

[24] Lynn B, Shacham H, Steiner M, et al. PBC Library[CP/OL]. [2016-12-20]. http://crypto.stanford.edu/pbc/

[25] Fiore D, Gennaro R. Making the Diffie-Hellman protocol identity-based[G] //LNCS 5985: Proc of Cryptographers’ Track at the RSA Conf. Berlin: Springer, 2010: 165-178

[26] Cheng Qingfeng, Ma Chuangui. Ephemeral key compromise attack on the IB-KA protocol[OL]. [2016-12-20]. http://eprint.iacr.org/2009/568

[27] Schnoor C P. Efficient signature generation for smart card[J]. Journal of Cryptology, 1991, 4(3): 161-174

[28] He Daojing, Chan S, Guizani M. Handover authentication for mobile networks: Security and efficiency aspects[J]. IEEE Network, 2015, 29(3): 96-103

StronglySecureAnonymousImplicitAuthenticationandKeyAgreementforRoamingService

Chen Ming

(CollegeofMathematicsandComputerScience,YichunUniversity,Yichun,Jiangxi336000) (StateKeyLaboratoryofTrustedComputingandInformationAssurance(InstituteofSoftware,ChineseAcademyofSciences),Beijing100190)

The existing two-party authentication and key agreement protocols for roaming service are provably secure in the CK model, and do not resist the attack of ephemeral secrets reveal. Based on elliptic curve cryptography and identity-based cryptosystem, we propose an anonymous two-party authentication and key agreement scheme for roaming service. The new scheme, based on the Schnorr signature, achieves mutual implicit authentication by a well designed “challenge-response” signature which is similar to the one in the HMQV protocol. We extend the ID-BJM model, a widely used security model for analyzing identity-based authenticated key agreement protocols, to simulate two-party authentication and key agreement schemes for roaming service. Furthermore, we demonstrate that the new scheme is eCK secure under the extended ID-BJM model, and that the security of the new scheme can be reduced to solve (by a polynomial-time adversary) computational Diffie- Hellman problems on an elliptic curve over finite fields. Comparative analysis shows that the new scheme has stronger security, achieves resistant to ephemeral secrets reveal, needs fewer cryptography libraries, and has lower computing, communication and storage overheads. The new scheme can be used to provide secure roaming authentication for resource constrained mobile terminals in global mobility networks, Internet of things or ubiquitous networks.

authenticated key agreement; mobile roaming service; identity-based cryptosystem; implicit authentication; computational Diffie-Hellman problem; eCK model

2016-06-28；

2017-07-04

国家自然科学基金项目(61662083)；江西省自然科学基金项目(2014ZBAB207022)；江西省教育厅科学技术研究项目(GJJ151040,GJJ151037)

This work was supported by the National Natural Science Foundation of China (61662083), the Natural Science Foundation of Jiangxi Province of China (2014ZBAB207022), and the Science & Technology Research Project of Jiangxi Provincial Education Department (GJJ151040, GJJ151037).

TP309

ChenMing, born in 1978. PhD. Member of the CCF. Lecturer of Yichun University. His main research interests include information security, security protocol and formal methods.